R - линейная регрессия
Регрессионный анализ - очень широко используемый статистический инструмент для установления модели взаимосвязи между двумя переменными. Одна из этих переменных называется переменной-предиктором, значение которой собирается в ходе экспериментов. Другая переменная называется переменной ответа, значение которой выводится из переменной-предиктора.
В линейной регрессии эти две переменные связаны уравнением, где показатель степени (степень) обеих этих переменных равен 1. Математически линейная зависимость представляет собой прямую линию, если она построена в виде графика. Нелинейная зависимость, когда показатель степени любой переменной не равен 1, создает кривую.
Общее математическое уравнение для линейной регрессии:
y = ax + bНиже приводится описание используемых параметров -
y переменная ответа.
x - предикторная переменная.
a и b - константы, которые называются коэффициентами.
Шаги по установлению регрессии
Простой пример регрессии - прогнозирование веса человека, когда известен его рост. Для этого нам необходимо иметь соотношение между ростом и весом человека.
Шаги по созданию отношений -
Проведите эксперимент по сбору выборки наблюдаемых значений роста и соответствующего веса.
Создайте модель отношений, используя lm() функции в R.
Найдите коэффициенты из созданной модели и создайте математическое уравнение, используя эти
Получите сводку модели отношений, чтобы узнать среднюю ошибку прогноза. Также называетсяresiduals.
Чтобы предсказать вес новых людей, используйте predict() функция в R.
Входные данные
Ниже приведены образцы данных, представляющих наблюдения -
# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131
# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48lm () Функция
Эта функция создает модель отношений между предиктором и переменной ответа.
Синтаксис
Базовый синтаксис для lm() функция в линейной регрессии -
lm(formula,data)Ниже приводится описание используемых параметров -
formula - символ, представляющий отношение между x и y.
data - вектор, к которому будет применяться формула.
Создать модель отношений и получить коэффициенты
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(relation)Когда мы выполняем приведенный выше код, он дает следующий результат:
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-38.4551 0.6746Получите краткое изложение отношений
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(summary(relation))Когда мы выполняем приведенный выше код, он дает следующий результат:
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-6.3002 -1.6629 0.0412 1.8944 3.9775
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -38.45509 8.04901 -4.778 0.00139 **
x 0.67461 0.05191 12.997 1.16e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared: 0.9548, Adjusted R-squared: 0.9491
F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06Функция predic ()
Синтаксис
Базовый синтаксис для predic () в линейной регрессии -
predict(object, newdata)Ниже приводится описание используемых параметров -
object это формула, которая уже создана с помощью функции lm ().
newdata вектор, содержащий новое значение переменной-предиктора.
Предсказать вес новых людей
# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <- predict(relation,a)
print(result)Когда мы выполняем приведенный выше код, он дает следующий результат:
1
76.22869Визуализируйте регрессию графически
# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)
# Give the chart file a name.
png(file = "linearregression.png")
# Plot the chart.
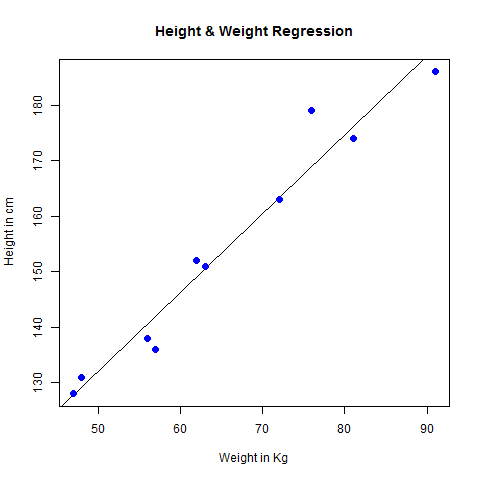
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")
# Save the file.
dev.off()Когда мы выполняем приведенный выше код, он дает следующий результат: