Transformer คู่กับเพาเวอร์แอมป์คลาส A

เพาเวอร์แอมป์คลาส A ตามที่กล่าวไว้ในบทที่แล้วคือวงจรที่กระแสเอาท์พุตไหลตลอดวงจรของแหล่งจ่ายไฟ AC เรายังได้เรียนรู้เกี่ยวกับข้อเสียที่มีเช่นกำลังขับและประสิทธิภาพต่ำ เพื่อลดเอฟเฟกต์เหล่านั้นให้น้อยที่สุดจึงมีการนำเอาเพาเวอร์แอมป์คลาส A ของหม้อแปลงมาใช้

construction of class A power amplifierสามารถเข้าใจได้ด้วยความช่วยเหลือของรูปด้านล่าง ซึ่งคล้ายกับวงจรแอมพลิฟายเออร์ปกติ แต่เชื่อมต่อกับหม้อแปลงในโหลดตัวเก็บรวบรวม

ที่นี่ R ₁และ R ₂ให้การจัดแบ่งที่เป็นไปได้ ตัวต้านทาน Re ให้ความเสถียร C _eคือตัวเก็บประจุบายพาสและ R _eเพื่อป้องกันแรงดันไฟฟ้ากระแสสลับ หม้อแปลงไฟฟ้าที่ใช้ที่นี่เป็นหม้อแปลงแบบ step-down

หลักอิมพีแดนซ์สูงของหม้อแปลงเชื่อมต่อกับวงจรสะสมอิมพีแดนซ์สูง ตัวรองอิมพีแดนซ์ต่ำเชื่อมต่อกับโหลด (โดยทั่วไปลำโพงจะดัง)

Transformer Action

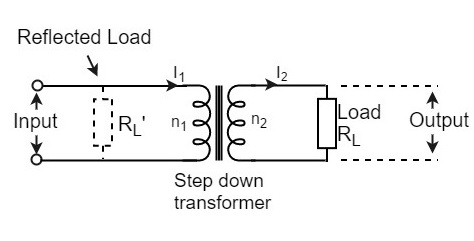
หม้อแปลงที่ใช้ในวงจรตัวสะสมมีไว้สำหรับการจับคู่อิมพีแดนซ์ R _Lคือโหลดที่เชื่อมต่อในตัวรองของหม้อแปลง R _L 'คือโหลดสะท้อนในส่วนหลักของหม้อแปลง

จำนวนรอบในเบื้องต้นมี n ₁และรอง n 2ให้ V ₁และ V ₂เป็นแรงดันไฟฟ้าหลักและรองและ I ₁และ I ₂เป็นกระแสหลักและรองตามลำดับ รูปด้านล่างแสดงหม้อแปลงอย่างชัดเจน

เรารู้ว่า

$$ \ frac {V_1} {V_2} = \ frac {n_1} {n_2} \: and \: \ frac {I_1} {I_2} = \ frac {n_1} {n_2} $$

หรือ

$$ V_1 = \ frac {n_1} {n_2} V_2 \: และ \: I_1 = \ frac {n_1} {n_2} I_2 $$

ดังนั้น

$$ \ frac {V_1} {I_1} = \ left (\ frac {n_1} {n_2} \ right) ^ 2 \ frac {V_2} {I_2} $$

แต่ V ₁ / I ₁ = R _L '= ความต้านทานอินพุตที่มีประสิทธิภาพ

และ V ₂ / I ₂ = R _L = ความต้านทานเอาต์พุตที่มีประสิทธิภาพ

ดังนั้น,

$$ R_L '= \ left (\ frac {n_1} {n_2} \ right) ^ 2 R_L = n ^ 2 R_L $$

ที่ไหน

$$ n = \ frac {number \: of \: turns \: in \: primary} {number \: of \: turns \: in \: secondary} = \ frac {n_1} {n_2} $$

เพาเวอร์แอมป์อาจจับคู่ได้โดยใช้อัตราส่วนการหมุนที่เหมาะสมในหม้อแปลงแบบ step down

การทำงานของวงจร

หากค่าสูงสุดของกระแสตัวสะสมเนื่องจากสัญญาณเท่ากับกระแสตัวรวบรวมสัญญาณเป็นศูนย์จะได้รับเอาต์พุตกำลังไฟ ac สูงสุด ดังนั้นเพื่อให้ได้การขยายที่สมบูรณ์จุดปฏิบัติการควรอยู่ที่กึ่งกลางของสายโหลด

เห็นได้ชัดว่าจุดปฏิบัติการแตกต่างกันไปเมื่อใช้สัญญาณ แรงดันไฟฟ้าของตัวสะสมจะแตกต่างกันไปในเฟสตรงข้ามกับกระแสของตัวสะสม การเปลี่ยนแปลงของแรงดันไฟฟ้าของตัวสะสมจะปรากฏขึ้นที่ส่วนหลักของหม้อแปลง

การวิเคราะห์วงจร

การสูญเสียพลังงานในขั้นต้นถือว่าน้อยมากเนื่องจากความต้านทานมีน้อยมาก

กำลังไฟฟ้าเข้าภายใต้สภาวะ dc จะเป็น

$$ (P_ {in}) _ {dc} = (P_ {tr}) _ {dc} = V_ {CC} \ times (I_C) _Q $$

ภายใต้ความจุสูงสุดของแอมพลิฟายเออร์คลาส A แรงดันไฟฟ้าจะเปลี่ยนจาก (V _ce ) _{สูงสุด}เป็นศูนย์และกระแสจาก (I _c ) _{สูงสุด}เป็นศูนย์

ดังนั้น

$$ V_ {rms} = \ frac {1} {\ sqrt {2}} \ left [\ frac {(V_ {ce}) _ {max} - (V_ {ce}) _ {min}} {2} \ right] = \ frac {1} {\ sqrt {2}} \ left [\ frac {(V_ {ce}) _ {max}} {2} \ right] = \ frac {2V_ {CC}} {2 \ sqrt {2}} = \ frac {V_ {CC}} {\ sqrt {2}} $$

$$ I_ {rms} = \ frac {1} {\ sqrt {2}} \ left [\ frac {(I_C) _ {max} - (I_C) _ {min}} {2} \ right] = \ frac {1} {\ sqrt {2}} \ left [\ frac {(I_C) _ {max}} {2} \ right] = \ frac {2 (I_C) _Q} {2 \ sqrt {2}} = \ frac {(I_C) _Q} {\ sqrt {2}} $$

ดังนั้น,

$$ (P_O) _ {ac} = V_ {rms} \ times I_ {rms} = \ frac {V_ {CC}} {\ sqrt {2}} \ times \ frac {(I_C) _Q} {\ sqrt { 2}} = \ frac {V_ {CC} \ times (I_C) _Q} {2} $$

ดังนั้น,

ประสิทธิภาพของนักสะสม = $ \ frac {(P_O) _ {ac}} {(P_ {tr}) _ {dc}} $

หรือ,

$$ (\ eta) _ {ตัวรวบรวม} = \ frac {V_ {CC} \ times (I_C) _Q} {2 \ times V_ {CC} \ times (I_C) _Q} = \ frac {1} {2} $ $

$$ = \ frac {1} {2} \ times 100 = 50 \% $$

ประสิทธิภาพของเพาเวอร์แอมป์คลาส A เกือบ 30% ในขณะที่ได้รับการปรับปรุงให้ดีขึ้นถึง 50% โดยใช้หม้อแปลงคู่กับเพาเวอร์แอมป์คลาส A