วิธีการจำแนกประเภทเบ็ดเตล็ด

ในที่นี้เราจะพูดถึงวิธีการจำแนกประเภทอื่น ๆ เช่น Genetic Algorithms, Rough Set Approach และ Fuzzy Set Approach

อัลกอริทึมทางพันธุกรรม

ความคิดของขั้นตอนวิธีทางพันธุกรรมได้มาจากวิวัฒนาการตามธรรมชาติ ในขั้นตอนวิธีทางพันธุกรรมก่อนอื่นจะมีการสร้างประชากรเริ่มต้น ประชากรเริ่มต้นนี้ประกอบด้วยกฎที่สร้างขึ้นแบบสุ่ม เราสามารถแทนกฎแต่ละข้อด้วยสตริงบิต

ตัวอย่างเช่นในชุดการฝึกอบรมที่กำหนดตัวอย่างจะอธิบายโดยคุณลักษณะบูลีนสองแบบเช่น A1 และ A2 และชุดฝึกที่ให้มานี้มีสองคลาสเช่น C1 และ C2

เราสามารถเข้ารหัสกฎ IF A1 AND NOT A2 THEN C2 เป็นสตริงบิต 100. ในการแทนค่าบิตนี้บิตซ้ายสุดสองบิตแทนแอตทริบิวต์ A1 และ A2 ตามลำดับ

ในทำนองเดียวกันกฎ IF NOT A1 AND NOT A2 THEN C1 สามารถเข้ารหัสเป็นไฟล์ 001.

Note- หากแอตทริบิวต์มีค่า K โดยที่ K> 2 เราสามารถใช้ K bits เพื่อเข้ารหัสค่าแอตทริบิวต์ได้ คลาสยังเข้ารหัสในลักษณะเดียวกัน

ข้อควรจำ -

• จากแนวคิดเรื่องการอยู่รอดของคนที่เหมาะสมที่สุดประชากรใหม่จะถูกสร้างขึ้นซึ่งประกอบด้วยกฎที่เหมาะสมที่สุดในประชากรปัจจุบันและค่านิยมของลูกหลานของกฎเหล่านี้เช่นกัน

• ความเหมาะสมของกฎถูกประเมินโดยความแม่นยำในการจำแนกประเภทของชุดตัวอย่างการฝึกอบรม

• ตัวดำเนินการทางพันธุกรรมเช่นการผสมข้ามและการกลายพันธุ์ถูกนำไปใช้เพื่อสร้างลูกหลาน

• ในการครอสโอเวอร์สตริงย่อยจากคู่ของกฎจะถูกสลับเพื่อสร้างคู่ใหม่ของกฎ

• ในการกลายพันธุ์บิตที่สุ่มเลือกในสตริงของกฎจะกลับด้าน

วิธีการตั้งค่าคร่าวๆ

เราสามารถใช้วิธีการตั้งค่าคร่าวๆเพื่อค้นหาความสัมพันธ์เชิงโครงสร้างภายในข้อมูลที่ไม่ชัดเจนและมีเสียงดัง

Note- แนวทางนี้ใช้ได้กับคุณลักษณะที่มีมูลค่าไม่ต่อเนื่องเท่านั้น ดังนั้นจึงต้องแยกแยะแอตทริบิวต์ที่มีมูลค่าต่อเนื่องก่อนใช้งาน

ทฤษฎีเซตหยาบขึ้นอยู่กับการสร้างคลาสการเทียบเท่าภายในข้อมูลการฝึกอบรมที่กำหนด tuples ที่สร้างคลาสความเท่าเทียมกันนั้นมองไม่เห็น หมายความว่าตัวอย่างเหมือนกันเมื่อเทียบกับคุณลักษณะที่อธิบายข้อมูล

มีบางคลาสในข้อมูลจริงที่ระบุซึ่งไม่สามารถแยกแยะได้ในแง่ของคุณลักษณะที่มีอยู่ เราสามารถใช้ชุดคร่าวๆเพื่อroughly กำหนดคลาสดังกล่าว

สำหรับคลาส C ที่กำหนดนิยามเซตคร่าวๆจะประมาณสองชุดดังนี้ -

• Lower Approximation of C - ค่าประมาณที่ต่ำกว่าของ C ประกอบด้วยข้อมูลทั้งหมดซึ่งขึ้นอยู่กับความรู้เกี่ยวกับแอตทริบิวต์นั้นแน่นอนว่าเป็นของคลาส C

• Upper Approximation of C - ค่าประมาณส่วนบนของ C ประกอบด้วยสิ่งทอทั้งหมดซึ่งขึ้นอยู่กับความรู้เกี่ยวกับคุณลักษณะไม่สามารถอธิบายได้ว่าไม่ได้เป็นของ C

แผนภาพต่อไปนี้แสดงการประมาณบนและล่างของคลาส C -

แนวทางการตั้งค่าที่ไม่ชัดเจน

Fuzzy Set Theory เรียกอีกอย่างว่าทฤษฎีความเป็นไปได้ ทฤษฎีนี้เสนอโดย Lotfi Zadeh ในปี 1965 เป็นอีกทางเลือกหนึ่งของtwo-value logic และ probability theory. ทฤษฎีนี้ช่วยให้เราสามารถทำงานในระดับสูงของนามธรรมได้ นอกจากนี้ยังให้วิธีการในการจัดการกับการวัดข้อมูลที่ไม่ชัดเจน

ทฤษฎีเซตฟัซซียังช่วยให้เราจัดการกับข้อเท็จจริงที่คลุมเครือหรือไม่ตรงประเด็น ตัวอย่างเช่นการเป็นสมาชิกของกลุ่มที่มีรายได้สูงนั้นแน่นอน (เช่นถ้า 50,000 ดอลลาร์สูงแล้ว 49,000 ดอลลาร์และ 48,000 ดอลลาร์) แตกต่างจากชุด CRISP แบบเดิมที่องค์ประกอบนั้นเป็นของ S หรือส่วนเสริม แต่ในทฤษฎีเซตที่คลุมเครือองค์ประกอบสามารถอยู่ในชุดฟัซซีได้มากกว่าหนึ่งชุด

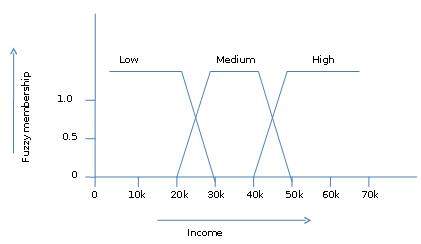
ตัวอย่างเช่นมูลค่ารายได้ 49,000 ดอลลาร์เป็นของทั้งชุดฟัซซี่ขนาดกลางและระดับสูง แต่มีระดับที่แตกต่างกัน สัญกรณ์ชุดฟัซซีสำหรับมูลค่ารายได้นี้มีดังนี้ -

mmedium_income($49k)=0.15 and mhigh_income($49k)=0.96

โดยที่ 'm' คือฟังก์ชันการเป็นสมาชิกที่ทำงานบนชุดฟัซซี่ของ medium_income และ high_income ตามลำดับ สัญกรณ์นี้สามารถแสดงเป็นแผนภาพได้ดังนี้ -