LISP - ต้นไม้

คุณสามารถสร้างโครงสร้างข้อมูลต้นไม้จากเซลล์จุดด้อยเป็นรายการของรายการ

ในการใช้โครงสร้างต้นไม้คุณจะต้องออกแบบฟังก์ชันที่จะเคลื่อนที่ผ่านเซลล์ข้อเสียตามลำดับที่เฉพาะเจาะจงตัวอย่างเช่นสั่งซื้อล่วงหน้าตามลำดับและหลังการสั่งซื้อสำหรับต้นไม้ไบนารี

ต้นไม้เป็นรายการของรายการ

ให้เราพิจารณาโครงสร้างต้นไม้ที่ประกอบด้วยเซลล์ข้อเสียซึ่งเป็นรายการต่อไปนี้ -

((1 2) (3 4) (5 6)).

ตามแผนภาพอาจแสดงเป็น -

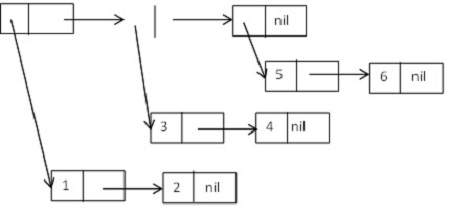
ฟังก์ชั่นต้นไม้ใน LISP

แม้ว่าส่วนใหญ่คุณจะต้องเขียนฟังก์ชันต้นไม้ของคุณเองตามความต้องการเฉพาะของคุณ LISP มีฟังก์ชันต้นไม้บางอย่างที่คุณสามารถใช้ได้

นอกเหนือจากฟังก์ชั่นรายการทั้งหมดแล้วฟังก์ชันต่อไปนี้ยังทำงานโดยเฉพาะกับโครงสร้างต้นไม้ -

ซีเนียร์	ฟังก์ชั่นและคำอธิบาย
1	copy-tree x & vecp เสริม ส่งคืนสำเนาของต้นไม้ของเซลล์ข้อเสีย x มันจะคัดลอกทั้งทิศทางรถและ cdr ซ้ำ ๆ ถ้า x ไม่ใช่เซลล์ข้อเสียฟังก์ชันจะคืนค่า x โดยไม่เปลี่ยนแปลง ถ้าอาร์กิวเมนต์ vecp ที่เป็นทางเลือกเป็นจริงฟังก์ชันนี้จะคัดลอกเวกเตอร์ (เรียกซ้ำ) รวมทั้งเซลล์ข้อเสีย
2	tree-equal xy & key: test: test-not: key มันเปรียบเทียบต้นไม้ข้อเสียสองเซลล์ ถ้า x และ y เป็นเซลล์จุดด้อยทั้งคู่รถและ cdrs จะถูกเปรียบเทียบแบบวนซ้ำ ถ้าทั้ง x หรือ y ไม่ใช่เซลล์จุดด้อยก็จะเปรียบเทียบโดย eql หรือตามการทดสอบที่ระบุ หากระบุฟังก์ชัน: คีย์จะถูกนำไปใช้กับองค์ประกอบของต้นไม้ทั้งสอง
3	subst ต้นไม้และคีย์เก่าใหม่: ทดสอบ: ทดสอบไม่ใช่: คีย์ มันแทนที่การเกิดขึ้นของรายการเก่าที่กำหนดด้วยรายการใหม่ในทรีซึ่งเป็นต้นไม้ของเซลล์ข้อเสีย
4	nsubst ต้นไม้และคีย์เก่าใหม่: ทดสอบ: ทดสอบไม่ใช่: คีย์ มันใช้งานได้เช่นเดียวกับการย่อย แต่มันทำลายต้นไม้เดิม
5	sublis alist tree & key: test: test-not: key มันทำงานเหมือน subst ยกเว้นว่าจะใช้เวลาในการเชื่อมโยงรายการalistของคู่เก่าใหม่ แต่ละองค์ประกอบของต้นไม้ (หลังจากใช้ฟังก์ชัน: key ถ้ามี) จะถูกเปรียบเทียบกับรถยนต์ของ alist หากตรงกันจะถูกแทนที่ด้วย cdr ที่เกี่ยวข้อง
6	nsublis alist tree & key: test: test-not: key มันใช้งานได้เหมือนกับ sublis แต่เป็นเวอร์ชันทำลายล้าง

ตัวอย่าง 1

สร้างไฟล์ซอร์สโค้ดใหม่ชื่อ main.lisp และพิมพ์รหัสต่อไปนี้

(setq lst (list '(1 2) '(3 4) '(5 6)))
(setq mylst (copy-list lst))
(setq tr (copy-tree lst))

(write lst)
(terpri)
(write mylst)
(terpri)
(write tr)

เมื่อคุณรันโค้ดจะส่งคืนผลลัพธ์ต่อไปนี้ -

((1 2) (3 4) (5 6))
((1 2) (3 4) (5 6))
((1 2) (3 4) (5 6))

ตัวอย่าง 2

สร้างไฟล์ซอร์สโค้ดใหม่ชื่อ main.lisp และพิมพ์รหัสต่อไปนี้

(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9)))))
(write tr)
(setq trs (subst 7 1 tr))
(terpri)
(write trs)

เมื่อคุณรันโค้ดจะส่งคืนผลลัพธ์ต่อไปนี้ -

((1 2 (3 4 5) ((7 8) (7 8 9))))
((7 2 (3 4 5) ((7 8) (7 8 9))))

สร้างต้นไม้ของคุณเอง

ให้เราลองสร้างต้นไม้ของเราเองโดยใช้ฟังก์ชันรายการที่มีอยู่ใน LISP

ขั้นแรกให้เราสร้างโหนดใหม่ที่มีข้อมูลบางส่วน

(defun make-tree (item)
   "it creates a new node with item."
   (cons (cons item nil) nil)
)

ต่อไปให้เราเพิ่มโหนดลูกลงในต้นไม้ - จะใช้โหนดต้นไม้สองโหนดและเพิ่มต้นไม้ที่สองเป็นลูกของต้นแรก

(defun add-child (tree child)
   (setf (car tree) (append (car tree) child))
   tree)

ฟังก์ชันนี้จะส่งคืนลูกคนแรกตามต้นไม้ที่กำหนด - จะใช้โหนดต้นไม้และส่งคืนลูกคนแรกของโหนดนั้นหรือไม่มีหากโหนดนี้ไม่มีโหนดลูก

(defun first-child (tree)
   (if (null tree)
      nil
      (cdr (car tree))
   )
)

ฟังก์ชันนี้จะส่งคืนพี่น้องถัดไปของโหนดที่กำหนดโดยใช้โหนดทรีเป็นอาร์กิวเมนต์และส่งคืนการอ้างอิงไปยังโหนดพี่น้องถัดไปหรือศูนย์หากโหนดไม่มีโหนดใด ๆ

(defun next-sibling (tree)
   (cdr tree)
)

สุดท้ายนี้เราต้องการฟังก์ชันเพื่อส่งคืนข้อมูลในโหนด -

(defun data (tree)
   (car (car tree))
)

ตัวอย่าง

ตัวอย่างนี้ใช้ฟังก์ชันข้างต้น -

สร้างไฟล์ซอร์สโค้ดใหม่ชื่อ main.lisp และพิมพ์รหัสต่อไปนี้

(defun make-tree (item)
   "it creates a new node with item."
   (cons (cons item nil) nil)
)
(defun first-child (tree)
   (if (null tree)
      nil
      (cdr (car tree))
   )
)

(defun next-sibling (tree)
   (cdr tree)
)
(defun data (tree)
   (car (car tree))
)
(defun add-child (tree child)
   (setf (car tree) (append (car tree) child))
   tree
)

(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9)))))
(setq mytree (make-tree 10))

(write (data mytree))
(terpri)
(write (first-child tr))
(terpri)
(setq newtree (add-child tr mytree))
(terpri)
(write newtree)

เมื่อคุณรันโค้ดจะส่งคืนผลลัพธ์ต่อไปนี้ -

10
(2 (3 4 5) ((7 8) (7 8 9)))

((1 2 (3 4 5) ((7 8) (7 8 9)) (10)))