SciPy - Hızlı Kılavuz
Sigh Pi olarak telaffuz edilen SciPy, Matematiksel, Bilimsel ve Mühendislik Hesaplamalarını gerçekleştirmek için BSD lisanslı kütüphane altında dağıtılan bilimsel bir python açık kaynağıdır.
SciPy kitaplığı, kullanışlı ve hızlı N boyutlu dizi manipülasyonu sağlayan NumPy'ye dayanır. SciPy kitaplığı, NumPy dizileriyle çalışmak üzere oluşturulmuştur ve sayısal entegrasyon ve optimizasyon rutinleri gibi birçok kullanıcı dostu ve verimli sayısal uygulama sağlar. Birlikte, tüm popüler işletim sistemlerinde çalışırlar, hızlı kurulurlar ve ücretsizdirler. NumPy ve SciPy'nin kullanımı kolaydır, ancak dünyanın önde gelen bilim adamları ve mühendislerinden bazıları tarafından güvenilecek kadar güçlüdür.
SciPy Alt paketleri
SciPy, farklı bilimsel hesaplama alanlarını kapsayan alt paketler halinde düzenlenmiştir. Bunlar aşağıdaki tabloda özetlenmiştir -
| scipy.cluster | Vektör niceleme / Kmeans |
| scipy.constants | Fiziksel ve matematiksel sabitler |
| scipy.fftpack | Fourier dönüşümü |
| scipy.integrate | Entegrasyon rutinleri |
| scipy.interpolate | İnterpolasyon |
| scipy.io | Veri girişi ve çıkışı |
| scipy.linalg | Doğrusal cebir rutinleri |
| scipy.ndimage | n boyutlu görüntü paketi |
| scipy.odr | Ortogonal mesafe regresyonu |
| scipy.optimize | Optimizasyon |
| scipy.signal | Sinyal işleme |
| scipy.sparse | Seyrek matrisler |
| scipy.spatial | Konumsal veri yapıları ve algoritmalar |
| scipy.special | Herhangi bir özel matematiksel fonksiyon |
| scipy.stats | İstatistik |
Veri yapısı
SciPy tarafından kullanılan temel veri yapısı, NumPy modülü tarafından sağlanan çok boyutlu bir dizidir. NumPy, Doğrusal Cebir, Fourier Dönüşümleri ve Rasgele Sayı Üretimi için bazı işlevler sağlar, ancak SciPy'deki eşdeğer işlevlerin genelliği ile birlikte değildir.
Standart Python dağıtımı herhangi bir SciPy modülüyle birlikte gelmez. Hafif bir alternatif, popüler Python paketi yükleyicisini kullanarak SciPy'yi kurmaktır.
pip install pandasEğer kurarsak Anaconda Python package, Pandalar varsayılan olarak yüklenecektir. Bunları farklı işletim sistemlerine kurmak için paketler ve bağlantılar aşağıdadır.
pencereler
Anaconda (kimden https://www.continuum.io) SciPy yığını için ücretsiz bir Python dağıtımıdır. Ayrıca Linux ve Mac için de mevcuttur.
Canopy (https://www.enthought.com/products/canopy/) ücretsiz ve Windows, Linux ve Mac için tam bir SciPy yığını ile ticari dağıtım için mevcuttur.
Python (x,y)- Windows işletim sistemi için SciPy yığını ve Spyder IDE içeren ücretsiz bir Python dağıtımıdır. (Adresinden indirilebilirhttps://python-xy.github.io/)
Linux
İlgili Linux dağıtımlarının paket yöneticileri, SciPy yığınına bir veya daha fazla paket yüklemek için kullanılır.
Ubuntu
Python'u Ubuntu'da kurmak için aşağıdaki yolu kullanabiliriz.
sudo apt-get install python-numpy python-scipy
python-matplotlibipythonipython-notebook python-pandas python-sympy python-noseFedora
Fedora'da Python kurmak için aşağıdaki yolu kullanabiliriz.
sudo yum install numpyscipy python-matplotlibipython python-pandas
sympy python-nose atlas-develVarsayılan olarak, tüm NumPy işlevleri SciPy ad alanı aracılığıyla kullanılabilir durumdadır. SciPy içe aktarıldığında NumPy işlevlerini açıkça içe aktarmaya gerek yoktur. NumPy'nin ana amacı homojen çok boyutlu dizidir. Bu, hepsi aynı türden, pozitif tamsayılardan oluşan bir demet ile indekslenmiş bir öğeler (genellikle sayılar) tablosudur. NumPy'de boyutlar eksen olarak adlandırılır. Sayısıaxes olarak adlandırılır rank.
Şimdi NumPy'de Vektörlerin ve Matrislerin temel işlevlerini gözden geçirelim. SciPy, NumPy dizilerinin üzerine kurulduğundan, NumPy temellerinin anlaşılması gerekir. Doğrusal cebirin çoğu bölümü yalnızca matrislerle ilgilendiğinden.
NumPy Vektör
Bir Vektör birden çok yolla oluşturulabilir. Bazıları aşağıda açıklanmıştır.
Python dizisi benzeri nesneleri NumPy'ye dönüştürme
Aşağıdaki örneği ele alalım.
import numpy as np
list = [1,2,3,4]
arr = np.array(list)
print arrYukarıdaki programın çıktısı aşağıdaki gibi olacaktır.
[1 2 3 4]İçsel NumPy Dizisi Oluşturma
NumPy, sıfırdan diziler oluşturmak için yerleşik işlevlere sahiptir. Bu işlevlerden bazıları aşağıda açıklanmıştır.
Sıfır kullanma ()
Sıfırlar (şekil) işlevi, belirtilen şekle sahip 0 değerlerle dolu bir dizi oluşturur. Varsayılan dtype float64'tür. Aşağıdaki örneği ele alalım.
import numpy as np
print np.zeros((2, 3))Yukarıdaki programın çıktısı aşağıdaki gibi olacaktır.
array([[ 0., 0., 0.],
[ 0., 0., 0.]])Bunları kullanma ()
Ones (şekil) işlevi 1 değerle dolu bir dizi oluşturacaktır. Diğer tüm açılardan sıfırlarla aynıdır. Aşağıdaki örneği ele alalım.
import numpy as np
print np.ones((2, 3))Yukarıdaki programın çıktısı aşağıdaki gibi olacaktır.
array([[ 1., 1., 1.],
[ 1., 1., 1.]])Arange () kullanma
Arange () işlevi, düzenli olarak artan değerlere sahip diziler oluşturacaktır. Aşağıdaki örneği ele alalım.
import numpy as np
print np.arange(7)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
array([0, 1, 2, 3, 4, 5, 6])Değerlerin veri tipini tanımlama
Aşağıdaki örneği ele alalım.
import numpy as np
arr = np.arange(2, 10, dtype = np.float)
print arr
print "Array Data Type :",arr.dtypeYukarıdaki program aşağıdaki çıktıyı üretecektir.
[ 2. 3. 4. 5. 6. 7. 8. 9.]
Array Data Type : float64Linspace () kullanma
Linspace () işlevi, belirtilen başlangıç ve bitiş değerleri arasında eşit aralıklarla yerleştirilecek belirli sayıda öğeye sahip diziler oluşturur. Aşağıdaki örneği ele alalım.
import numpy as np
print np.linspace(1., 4., 6)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
array([ 1. , 1.6, 2.2, 2.8, 3.4, 4. ])Matris
Bir matris, 2 boyutlu doğasını işlemler yoluyla koruyan özel bir 2 boyutlu dizidir. * (Matris çarpımı) ve ** (matris gücü) gibi bazı özel operatörlere sahiptir. Aşağıdaki örneği ele alalım.
import numpy as np
print np.matrix('1 2; 3 4')Yukarıdaki program aşağıdaki çıktıyı üretecektir.
matrix([[1, 2],
[3, 4]])Matrisin Eşlenik Transpozesi
Bu özellik, (karmaşık) eşlenik devrikini döndürür self. Aşağıdaki örneği ele alalım.
import numpy as np
mat = np.matrix('1 2; 3 4')
print mat.HYukarıdaki program aşağıdaki çıktıyı üretecektir.
matrix([[1, 3],
[2, 4]])Matrisin Transpoze Edilmesi
Bu özellik, kendiliğin devrikini döndürür. Aşağıdaki örneği ele alalım.
import numpy as np
mat = np.matrix('1 2; 3 4')
mat.TYukarıdaki program aşağıdaki çıktıyı üretecektir.
matrix([[1, 3],
[2, 4]])Bir matrisi transpoze ettiğimizde, satırları orijinalin sütunları olan yeni bir matris oluştururuz. Öte yandan bir eşlenik transpozisyonu, her bir matris elemanı için satır ve sütun indeksini değiştirir. Bir matrisin tersi, orijinal matrisle çarpıldığında bir kimlik matrisiyle sonuçlanan bir matristir.
K-means clusteringetiketlenmemiş bir veri kümesinde kümeleri ve küme merkezlerini bulmak için bir yöntemdir. Sezgisel olarak, bir kümeyi - noktalar arası mesafeleri kümenin dışındaki noktalara olan mesafelere kıyasla küçük olan bir grup veri noktasından oluşan bir grup olarak düşünebiliriz. Başlangıçta bir K merkezi kümesi verildiğinde, K-ortalama algoritması aşağıdaki iki adımı yineler:
Her merkez için, ona daha yakın olan eğitim noktalarının alt kümesi (kümelenmesi), diğer herhangi bir merkezden daha fazla belirlenir.
Her kümedeki veri noktalarının her bir özelliğinin ortalaması hesaplanır ve bu ortalama vektör, o kümenin yeni merkezi olur.
Bu iki adım, merkezler artık hareket etmeyene veya atamalar artık değişmeyene kadar yinelenir. Sonra yeni bir noktaxen yakın prototip kümesine atanabilir. SciPy kütüphanesi, küme paketi aracılığıyla K-Means algoritmasının iyi bir uygulamasını sağlar. Nasıl kullanılacağını anlayalım.
SciPy'de K-Means Uygulaması
SciPy'de K-Means'in nasıl uygulanacağını anlayacağız.
K-Ortalamalarını İçe Aktar
İçe aktarılan her işlevin uygulanmasını ve kullanımını göreceğiz.
from SciPy.cluster.vq import kmeans,vq,whitenVeri üretimi
Kümelemeyi keşfetmek için bazı verileri simüle etmeliyiz.
from numpy import vstack,array
from numpy.random import rand
# data generation with three features
data = vstack((rand(100,3) + array([.5,.5,.5]),rand(100,3)))Şimdi, verileri kontrol etmeliyiz. Yukarıdaki program aşağıdaki çıktıyı üretecektir.
array([[ 1.48598868e+00, 8.17445796e-01, 1.00834051e+00],
[ 8.45299768e-01, 1.35450732e+00, 8.66323621e-01],
[ 1.27725864e+00, 1.00622682e+00, 8.43735610e-01],
…………….Özellik bazında bir gözlem grubunu normalleştirin. K-Ortalamaları çalıştırmadan önce gözlem setinin her bir özellik boyutunu beyazlatma ile yeniden ölçeklendirmek faydalıdır. Her özellik, birim varyansını vermek için tüm gözlemlerdeki standart sapmasına bölünür.
Verileri beyazlatın
Verileri beyazlatmak için aşağıdaki kodu kullanmalıyız.
# whitening of data
data = whiten(data)Üç Küme ile K-Means Hesaplama
Şimdi aşağıdaki kodu kullanarak üç küme ile K-Ortalamalarını hesaplayalım.
# computing K-Means with K = 3 (2 clusters)
centroids,_ = kmeans(data,3)Yukarıdaki kod, K kümelerini oluşturan bir dizi gözlem vektörü üzerinde K-Ortalamalarını gerçekleştirir. K-Means algoritması, yeterli ilerleme sağlanamayana kadar ağırlık merkezlerini ayarlar, yani son yineleme bazı eşik değerlerinin altında olduğu için distorsiyondaki değişiklik. Burada, aşağıda verilen kodu kullanarak centroids değişkenini yazdırarak kümenin centroidini gözlemleyebiliriz.
print(centroids)Yukarıdaki kod aşağıdaki çıktıyı üretecektir.
print(centroids)[ [ 2.26034702 1.43924335 1.3697022 ]
[ 2.63788572 2.81446462 2.85163854]
[ 0.73507256 1.30801855 1.44477558] ]Aşağıda verilen kodu kullanarak her bir değeri bir kümeye atayın.
# assign each sample to a cluster
clx,_ = vq(data,centroids)vq fonksiyonu 'M' içindeki her gözlem vektörünü 'N' ile karşılaştırır obscentroidlerle dizi ve gözlemi en yakın kümeye atar. Her gözlemin kümesini ve bozulmayı döndürür. Bozulmayı da kontrol edebiliriz. Aşağıdaki kodu kullanarak her gözlemin kümesini kontrol edelim.
# check clusters of observation
print clxYukarıdaki kod aşağıdaki çıktıyı üretecektir.
array([1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 2, 0, 2, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0,
0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0,
2, 2, 2, 1, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int32)Yukarıdaki dizinin farklı değerleri 0, 1, 2 kümeleri gösterir.
SciPy sabitleri paketi, genel bilimsel alanda kullanılan çok çeşitli sabitler sağlar.
SciPy Sabitler Paketi
scipy.constants packageçeşitli sabitler sağlar. Gerekli sabiti ithal etmeli ve ihtiyaca göre kullanmalıyız. Bu sabit değişkenlerin nasıl içe aktarıldığını ve kullanıldığını görelim.
Başlangıç olarak, aşağıdaki örneği dikkate alarak 'pi' değerini karşılaştıralım.
#Import pi constant from both the packages
from scipy.constants import pi
from math import pi
print("sciPy - pi = %.16f"%scipy.constants.pi)
print("math - pi = %.16f"%math.pi)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
sciPy - pi = 3.1415926535897931
math - pi = 3.1415926535897931Mevcut Sabitler Listesi
Aşağıdaki tablolar, çeşitli sabitleri kısaca açıklamaktadır.
Matematiksel Sabitler
| Sr. No. | Sabit | Açıklama |
|---|---|---|
| 1 | pi | pi |
| 2 | altın | Altın Oran |
Fiziksel Sabitler
Aşağıdaki tablo en sık kullanılan fiziksel sabitleri listeler.
| Sr. No. | Sabit ve Açıklama |
|---|---|
| 1 | c Vakumda ışık hızı |
| 2 | speed_of_light Vakumda ışık hızı |
| 3 | h Planck sabiti |
| 4 | Planck Planck sabiti h |
| 5 | G Newton'un yerçekimi sabiti |
| 6 | e Temel ücret |
| 7 | R Molar gaz sabiti |
| 8 | Avogadro Avogadro sabiti |
| 9 | k Boltzmann sabiti |
| 10 | electron_mass(OR) m_e Elektronik kütle |
| 11 | proton_mass (OR) m_p Proton kütlesi |
| 12 | neutron_mass(OR)m_n Nötron kütlesi |
Birimler
Aşağıdaki tabloda SI birimlerinin listesi bulunmaktadır.
| Sr. No. | Birim | Değer |
|---|---|---|
| 1 | milli | 0.001 |
| 2 | mikro | 1e-06 |
| 3 | kilo | 1000 |
Bu birimler yotta, zetta, exa, peta, tera …… kilo, hector,… nano, pico,… ve zepto arasında değişir.
Diğer Önemli Sabitler
Aşağıdaki tablo SciPy'de kullanılan diğer önemli sabitleri listeler.
| Sr. No. | Birim | Değer |
|---|---|---|
| 1 | gram | 0,001 kg |
| 2 | atom kütlesi | Atomik kütle sabiti |
| 3 | derece | Radyan cinsinden derece |
| 4 | dakika | Saniyeler içinde bir dakika |
| 5 | gün | Saniyeler içinde bir gün |
| 6 | inç | Metre cinsinden bir inç |
| 7 | mikron | Metre cinsinden bir mikron |
| 8 | ışık yılı | Metre cinsinden bir ışık yılı |
| 9 | ATM | Pascallarda standart atmosfer |
| 10 | dönüm | Metrekare olarak bir dönüm |
| 11 | litre | Metreküp cinsinden bir litre |
| 12 | galon | Metreküp cinsinden bir galon |
| 13 | kmh | Saniyede metre cinsinden saat başına kilometre |
| 14 | derece_Fahrenheit | Kelvin cinsinden bir Fahrenheit |
| 15 | eV | Joule cinsinden bir elektron volt |
| 16 | hp | Watt cinsinden bir beygir gücü |
| 17 | dyn | Newton'da bir dyne |
| 18 | lambda2nu | Dalgaboyunu optik frekansa dönüştürme |
Bunların hepsini hatırlamak biraz zor. Hangi tuşun hangi işlev için olduğunu öğrenmenin kolay yolu,scipy.constants.find()yöntem. Aşağıdaki örneği ele alalım.
import scipy.constants
res = scipy.constants.physical_constants["alpha particle mass"]
print resYukarıdaki program aşağıdaki çıktıyı üretecektir.
[
'alpha particle mass',
'alpha particle mass energy equivalent',
'alpha particle mass energy equivalent in MeV',
'alpha particle mass in u',
'electron to alpha particle mass ratio'
]Bu yöntem anahtar listesini döndürür, aksi takdirde anahtar kelime eşleşmezse hiçbir şey döndürmez.
Fourier Transformationfrekans alanındaki davranışını kontrol etmek için bir zaman alanı sinyali üzerinde hesaplanır. Fourier dönüşümü, uygulamasını sinyal ve gürültü işleme, görüntü işleme, ses sinyali işleme, vb. Gibi disiplinlerde bulur. SciPy, kullanıcının hızlı Fourier dönüşümlerini hesaplamasını sağlayan fftpack modülünü sunar.
Aşağıda, fftpack modülünü kullanarak Fourier dönüşümünü hesaplamak için kullanılacak bir sinüs işlevi örneği verilmiştir.
Hızlı Fourier Dönüşümü
Fourier dönüşümünün ne kadar hızlı olduğunu ayrıntılı olarak anlayalım.
Tek Boyutlu Ayrık Fourier Dönüşümü
Uzunluk-N dizisi x [n] 'nin N uzunluğunun FFT y [k] değeri fft () ile hesaplanır ve ters dönüşüm ifft () kullanılarak hesaplanır. Aşağıdaki örneği ele alalım
#Importing the fft and inverse fft functions from fftpackage
from scipy.fftpack import fft
#create an array with random n numbers
x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
#Applying the fft function
y = fft(x)
print yYukarıdaki program aşağıdaki çıktıyı üretecektir.
[ 4.50000000+0.j 2.08155948-1.65109876j -1.83155948+1.60822041j
-1.83155948-1.60822041j 2.08155948+1.65109876j ]Başka bir örneğe bakalım
#FFT is already in the workspace, using the same workspace to for inverse transform
yinv = ifft(y)
print yinvYukarıdaki program aşağıdaki çıktıyı üretecektir.
[ 1.0+0.j 2.0+0.j 1.0+0.j -1.0+0.j 1.5+0.j ]scipy.fftpackmodülü, hızlı Fourier dönüşümlerinin hesaplanmasına izin verir. Örnek olarak, (gürültülü) bir giriş sinyali aşağıdaki gibi görünebilir -
import numpy as np
time_step = 0.02
period = 5.
time_vec = np.arange(0, 20, time_step)
sig = np.sin(2 * np.pi / period * time_vec) + 0.5 *np.random.randn(time_vec.size)
print sig.size0.02 saniyelik zaman adımlı bir sinyal oluşturuyoruz. Son ifade, sinyal sinyalinin boyutunu yazdırır. Çıktı aşağıdaki gibi olacaktır -
1000Sinyal frekansını bilmiyoruz; biz sadece sinyal işaretinin örnekleme zaman adımını biliyoruz. Sinyalin gerçek bir fonksiyondan geldiği varsayılır, bu nedenle Fourier dönüşümü simetrik olacaktır. scipy.fftpack.fftfreq() işlevi örnekleme frekanslarını oluşturacak ve scipy.fftpack.fft() hızlı Fourier dönüşümünü hesaplayacaktır.
Bunu bir örnek yardımıyla anlayalım.
from scipy import fftpack
sample_freq = fftpack.fftfreq(sig.size, d = time_step)
sig_fft = fftpack.fft(sig)
print sig_fftYukarıdaki program aşağıdaki çıktıyı üretecektir.
array([
25.45122234 +0.00000000e+00j, 6.29800973 +2.20269471e+00j,
11.52137858 -2.00515732e+01j, 1.08111300 +1.35488579e+01j,
…….])Ayrık kosinüs dönüşümü
Bir Discrete Cosine Transform (DCT)farklı frekanslarda salınan kosinüs fonksiyonlarının toplamı cinsinden sonlu bir veri noktaları dizisini ifade eder. SciPy işlevi ile bir DCT sağlardct ve işlevi ile karşılık gelen bir IDCT idct. Aşağıdaki örneği ele alalım.
from scipy.fftpack import dct
print dct(np.array([4., 3., 5., 10., 5., 3.]))Yukarıdaki program aşağıdaki çıktıyı üretecektir.
array([ 60., -3.48476592, -13.85640646, 11.3137085, 6., -6.31319305])Ters ayrık kosinüs dönüşümü, ayrık kosinüs dönüşümü (DCT) katsayılarından bir diziyi yeniden oluşturur. İdct işlevi, dct işlevinin tersidir. Bunu aşağıdaki örnekle anlayalım.
from scipy.fftpack import dct
print idct(np.array([4., 3., 5., 10., 5., 3.]))Yukarıdaki program aşağıdaki çıktıyı üretecektir.
array([ 39.15085889, -20.14213562, -6.45392043, 7.13341236,
8.14213562, -3.83035081])Bir fonksiyon analitik olarak entegre edilemediğinde veya analitik olarak entegre edilmesi çok zor olduğunda, kişi genellikle sayısal entegrasyon yöntemlerine yönelir. SciPy, sayısal entegrasyon gerçekleştirmek için bir dizi rutine sahiptir. Çoğu aynı yerde bulunurscipy.integratekütüphane. Aşağıdaki tablo yaygın olarak kullanılan bazı işlevleri listelemektedir.
| Sr Hayır. | İşlev ve Açıklama |
|---|---|
| 1 | quad Tek entegrasyon |
| 2 | dblquad Çift entegrasyon |
| 3 | tplquad Üçlü entegrasyon |
| 4 | nquad n katlamalı çoklu entegrasyon |
| 5 | fixed_quad Gauss kuadratürü, sıra n |
| 6 | quadrature Toleransa Gauss kuadratürü |
| 7 | romberg Romberg entegrasyonu |
| 8 | trapz Trapez kuralı |
| 9 | cumtrapz İntegrali kümülatif olarak hesaplamak için yamuk kuralı |
| 10 | simps Simpson kuralı |
| 11 | romb Romberg entegrasyonu |
| 12 | polyint Analitik polinom entegrasyonu (NumPy) |
| 13 | poly1d Polyint için yardımcı işlev (NumPy) |
Tek İntegraller
Quad işlevi, SciPy'nin entegrasyon işlevlerinin en önemli unsurudur. Sayısal entegrasyon bazen denirquadrature, dolayısıyla adı. Normalde, bir f (x) fonksiyonunun tekli integrallerini a'dan b'ye belirli bir sabit aralıkta gerçekleştirmek için varsayılan seçimdir .
$$\int_{a}^{b} f(x)dx$$
Quad'ın genel şekli scipy.integrate.quad(f, a, b), Burada 'f', entegre edilecek işlevin adıdır. Oysa 'a' ve 'b' sırasıyla alt ve üst sınırlardır. 0 ve 1 aralığında entegre edilmiş bir Gauss işlevi örneği görelim.
Önce işlevi tanımlamamız gerekiyor → $f(x) = e^{-x^2}$ , bu bir lambda ifadesi kullanılarak yapılabilir ve ardından bu işlevde dörtlü yöntem çağırılabilir.
import scipy.integrate
from numpy import exp
f= lambda x:exp(-x**2)
i = scipy.integrate.quad(f, 0, 1)
print iYukarıdaki program aşağıdaki çıktıyı üretecektir.
(0.7468241328124271, 8.291413475940725e-15)Quad işlevi, ilk sayının integralin değeri ve ikinci değerin, integralin değerindeki mutlak hatanın tahmini olduğu iki değeri döndürür.
NoteQuad işlevi ilk argüman olarak gerektirdiğinden, bağımsız değişken olarak doğrudan exp geçiremeyiz. Quad işlevi, pozitif ve negatif sonsuzluğu sınırlar olarak kabul eder. Quad fonksiyonu, exp, sin ve cos gibi tek bir değişkenin standart önceden tanımlanmış NumPy fonksiyonlarını entegre edebilir.
Çoklu İntegraller
İkili ve üçlü entegrasyon mekaniği, işlevlere dahil edilmiştir dblquad, tplquad ve nquad. Bu işlevler sırasıyla dört veya altı argümanı birleştirir. Tüm iç integrallerin sınırları fonksiyonlar olarak tanımlanmalıdır.
Çift İntegraller
Genel formu dblquadscipy.integrate.dblquad'dir (func, a, b, gfun, hfun). Burada, func entegre edilecek fonksiyonun adıdır, 'a' ve 'b' sırasıyla x değişkeninin alt ve üst limitleri iken, gfun ve hfun alt ve üst limitleri tanımlayan fonksiyonların isimleridir. y değişkeninin.
Örnek olarak, çift katlı integral yöntemini uygulayalım.
$$\int_{0}^{1/2} dy \int_{0}^{\sqrt{1-4y^2}} 16xy \:dx$$
Lambda ifadelerini kullanarak f, g ve h fonksiyonlarını tanımlıyoruz. G ve h sabit olsalar bile, çoğu durumda olduğu gibi, burada alt sınır için yaptığımız gibi, fonksiyonlar olarak tanımlanmaları gerektiğini unutmayın.
import scipy.integrate
from numpy import exp
from math import sqrt
f = lambda x, y : 16*x*y
g = lambda x : 0
h = lambda y : sqrt(1-4*y**2)
i = scipy.integrate.dblquad(f, 0, 0.5, g, h)
print iYukarıdaki program aşağıdaki çıktıyı üretecektir.
(0.5, 1.7092350012594845e-14)Scipy.integrate, yukarıda açıklanan rutinlere ek olarak, n-kat çoklu entegrasyon gerçekleştiren nquad ve çeşitli entegrasyon algoritmalarını uygulayan diğer rutinler dahil olmak üzere bir dizi başka entegrasyon rutinine sahiptir. Ancak, quad ve dblquad, sayısal entegrasyon ihtiyacımızın çoğunu karşılayacaktır.
Bu bölümde, interpolasyonun SciPy'de nasıl yardımcı olduğunu tartışacağız.
İnterpolasyon nedir?
Enterpolasyon, bir çizgi veya bir eğri üzerindeki iki nokta arasında bir değer bulma işlemidir. Ne anlama geldiğini hatırlamamıza yardımcı olmak için, 'inter' kelimesinin ilk bölümünü 'enter' anlamında düşünmeliyiz ve bu bize başlangıçta sahip olduğumuz verilerin 'içine' bakmamızı hatırlatır. Bu araç, enterpolasyon, yalnızca istatistikte yararlı değildir, aynı zamanda bilimde, iş dünyasında veya mevcut iki veri noktasında yer alan değerleri tahmin etme ihtiyacı olduğunda da yararlıdır.
Biraz veri oluşturalım ve bu enterpolasyonun nasıl yapılabileceğini görelim. scipy.interpolate paketi.
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print x,yYukarıdaki program aşağıdaki çıktıyı üretecektir.
(
array([0., 0.36363636, 0.72727273, 1.09090909, 1.45454545, 1.81818182,
2.18181818, 2.54545455, 2.90909091, 3.27272727, 3.63636364, 4.]),
array([-0.65364362, -0.61966189, -0.51077021, -0.31047698, -0.00715476,
0.37976236, 0.76715099, 0.99239518, 0.85886263, 0.27994201,
-0.52586509, -0.99582185])
)Şimdi iki dizimiz var. Bu iki diziyi uzaydaki noktaların iki boyutu olarak varsayarak, aşağıdaki programı kullanarak grafiğini çizelim ve nasıl göründüklerini görelim.
plt.plot(x, y,’o’)
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.
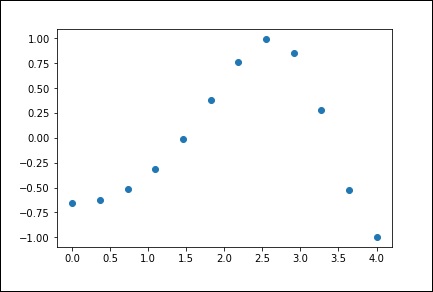
1-D Enterpolasyon
Scipy.interpolate içindeki interp1d sınıfı, doğrusal enterpolasyon kullanılarak verilen veriler tarafından tanımlanan etki alanı içinde herhangi bir yerde değerlendirilebilen sabit veri noktalarına dayalı bir işlev oluşturmak için uygun bir yöntemdir.
Yukarıdaki verileri kullanarak, bir enterpolasyon fonksiyonu oluşturalım ve yeni bir enterpolasyonlu grafik çizelim.
f1 = interp1d(x, y,kind = 'linear')
f2 = interp1d(x, y, kind = 'cubic')İnterp1d işlevini kullanarak f1 ve f2 olmak üzere iki işlev oluşturduk. Bu işlevler, belirli bir girdi için x, y'yi döndürür. Üçüncü değişken türü, enterpolasyon tekniğinin türünü temsil eder. 'Doğrusal', 'En Yakın', 'Sıfır', 'Slinear', 'Karesel', 'Kübik' birkaç enterpolasyon tekniğidir.
Şimdi, enterpolasyonun açık farkını görmek için daha uzun yeni bir girdi oluşturalım. Yeni verilerde eski verilerin aynı işlevini kullanacağız.
xnew = np.linspace(0, 4,30)
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.
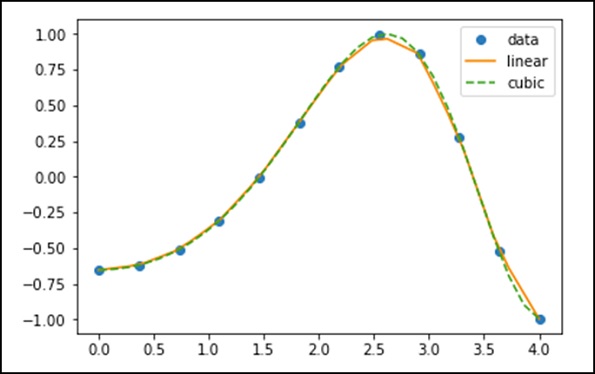
Spline'lar
Veri noktalarından düzgün eğriler çizmek için, bir zamanlar teknik ressamlar mekanik yiv adı verilen ince esnek ahşap, sert kauçuk, metal veya plastik şeritleri kullandılar. Mekanik bir spline kullanmak için, pimler bir tasarımdaki bir eğri boyunca makul bir şekilde seçilen noktalara yerleştirildi ve daha sonra spline, bu pimlerin her birine dokunacak şekilde büküldü.
Açıkça, bu yapıyla, spline bu pinlerdeki eğriyi enterpolasyonlu hale getirir. Diğer çizimlerde eğriyi yeniden oluşturmak için kullanılabilir. Pimlerin bulunduğu noktalara düğüm denir. Düğümlerin konumunu ayarlayarak eğri tarafından tanımlanan eğrinin şeklini değiştirebiliriz.
Tek Değişkenli Spline
Tek boyutlu yumuşatma eğrisi, belirli bir veri noktası kümesine uyar. Scipy.interpolate içindeki UnivariateSpline sınıfı, sabit veri noktaları sınıfına - scipy.interpolate.UnivariateSpline (x, y, w = None, bbox = [None, None], k = 3, s) dayalı bir işlev oluşturmak için uygun bir yöntemdir = Yok, ext = 0, check_finite = False).
Parameters - Aşağıda Univariate Spline'ın parametreleri verilmiştir.
Bu, sağlanan x, y verilerine k dereceli bir y = spl (x) eğri uydurur.
'w' - Eğri uydurma için ağırlıkları belirtir. Olumlu olmalı. Hiçbiri değilse (varsayılan), ağırlıkların tümü eşittir.
's' - Bir yumuşatma koşulu belirterek düğüm sayısını belirtir.
'k' - Düzleştirme eğrisinin derecesi. <= 5 olmalıdır. Varsayılan k = 3, kübik bir spline'dır.
Ext - Düğüm dizisi tarafından tanımlanan aralıkta olmayan öğeler için ekstrapolasyon modunu kontrol eder.
ext = 0 veya 'extrapolate' ise, tahmini değeri döndürür.
ext = 1 veya 'sıfır' ise 0 döndürür
ext = 2 veya 'yükseltme' ise, bir Değer Hatası yükseltir
ext = 3 'const' ise, sınır değerini döndürür.
check_finite - Giriş dizilerinin yalnızca sonlu sayılar içerdiğinin kontrol edilip edilmeyeceği.
Aşağıdaki örneği ele alalım.
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.plot(x, y, 'ro', ms = 5)
plt.show()Düzeltme parametresi için varsayılan değeri kullanın.
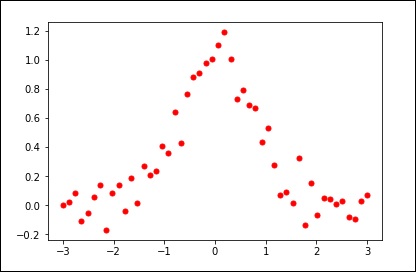
spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()Düzeltme miktarını manuel olarak değiştirin.
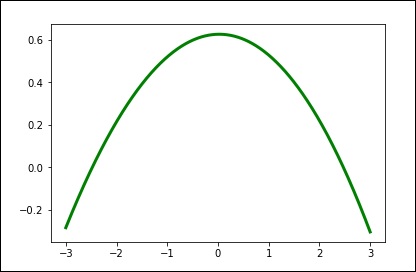
spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()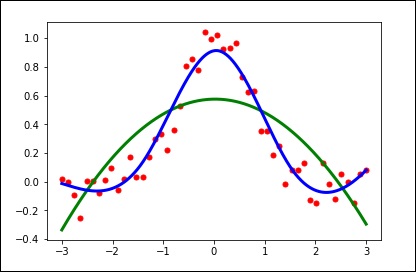
Scipy.io (Girdi ve Çıktı) paketi, farklı dosya biçimleriyle çalışmak için çok çeşitli işlevler sağlar. Bu biçimlerden bazıları -
- Matlab
- IDL
- Matrix Pazarı
- Wave
- Arff
- Netcdf vb.
En sık kullanılan dosya formatları hakkında ayrıntılı olarak tartışalım -
MATLAB
Bir .mat dosyasını yüklemek ve kaydetmek için kullanılan işlevler aşağıdadır.
| Sr. No. | İşlev ve Açıklama |
|---|---|
| 1 | loadmat MATLAB dosyası yükler |
| 2 | savemat MATLAB dosyası kaydeder |
| 3 | whosmat MATLAB dosyasındaki değişkenleri listeler |
Aşağıdaki örneği ele alalım.
import scipy.io as sio
import numpy as np
#Save a mat file
vect = np.arange(10)
sio.savemat('array.mat', {'vect':vect})
#Now Load the File
mat_file_content = sio.loadmat(‘array.mat’)
Print mat_file_contentYukarıdaki program aşağıdaki çıktıyı üretecektir.
{
'vect': array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]), '__version__': '1.0',
'__header__': 'MATLAB 5.0 MAT-file Platform: posix, Created on: Sat Sep 30
09:49:32 2017', '__globals__': []
}Diziyi Meta bilgileriyle birlikte görebiliriz. Verileri belleğe okumadan bir MATLAB dosyasının içeriğini incelemek istiyorsak,whosmat command Aşağıda gösterildiği gibi.
import scipy.io as sio
mat_file_content = sio.whosmat(‘array.mat’)
print mat_file_contentYukarıdaki program aşağıdaki çıktıyı üretecektir.
[('vect', (1, 10), 'int64')]SciPy, optimize edilmiş ATLAS LAPACK ve BLASkütüphaneler. Çok hızlı doğrusal cebir yeteneklerine sahiptir. Tüm bu doğrusal cebir rutinleri, iki boyutlu bir diziye dönüştürülebilen bir nesneyi bekler. Bu rutinlerin çıktısı da iki boyutlu bir dizidir.
SciPy.linalg ve NumPy.linalg
Scipy.linalg, numpy.linalg içindeki tüm işlevleri içerir. Ek olarak, scipy.linalg ayrıca numpy.linalg'de olmayan bazı gelişmiş işlevlere de sahiptir. Numpy.linalg yerine scipy.linalg kullanmanın bir başka avantajı, her zaman BLAS / LAPACK desteği ile derlenmiş olmasıdır, NumPy için ise bu isteğe bağlıdır. Bu nedenle, SciPy sürümü NumPy'nin nasıl kurulduğuna bağlı olarak daha hızlı olabilir.
Doğrusal Denklemler
scipy.linalg.solve özelliği bilinmeyen x, y değerleri için a * x + b * y = Z doğrusal denklemini çözer.
Örnek olarak, aşağıdaki eşzamanlı denklemlerin çözülmesinin istendiğini varsayalım.
x + 3y + 5z = 10
2x + 5y + z = 8
2x + 3y + 8z = 3
X, y, z değerleri için yukarıdaki denklemi çözmek için, aşağıda gösterildiği gibi bir matris tersini kullanarak çözüm vektörünü bulabiliriz.
$$\begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8 \end{bmatrix}^{-1} \begin{bmatrix} 10\\ 8\\ 3 \end{bmatrix} = \frac{1}{25} \begin{bmatrix} -232\\ 129\\ 19 \end{bmatrix} = \begin{bmatrix} -9.28\\ 5.16\\ 0.76 \end{bmatrix}.$$
Ancak, kullanmak daha iyidir linalg.solve Daha hızlı ve sayısal olarak daha kararlı olabilen komut.
Çözüm işlevi, 'a' nın katsayıları temsil ettiği ve 'b'nin ilgili sağ taraftaki değeri temsil ettiği ve çözüm dizisini döndürdüğü' a 've' b 'iki girdisini alır.
Aşağıdaki örneği ele alalım.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy arrays
a = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]])
b = np.array([2, 4, -1])
#Passing the values to the solve function
x = linalg.solve(a, b)
#printing the result array
print xYukarıdaki program aşağıdaki çıktıyı üretecektir.
array([ 2., -2., 9.])Belirleyici Bulmak
A kare matrisinin determinantı genellikle | A | olarak gösterilir. ve genellikle doğrusal cebirde kullanılan bir niceliktir. SciPy'de bu,det()işlevi. Girdi olarak bir matris alır ve skaler bir değer döndürür.
Aşağıdaki örneği ele alalım.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the det function
x = linalg.det(A)
#printing the result
print xYukarıdaki program aşağıdaki çıktıyı üretecektir.
-2.0Özdeğerler ve özvektörler
Özdeğer-özvektör problemi, en yaygın kullanılan doğrusal cebir işlemlerinden biridir. Aşağıdaki ilişkiyi göz önünde bulundurarak bir kare matrisin (A) öz değerlerini (λ) ve karşılık gelen Eigen vektörlerini (v) bulabiliriz -
Av = λv
scipy.linalg.eigSıradan veya genelleştirilmiş bir özdeğer probleminden özdeğerleri hesaplar. Bu işlev, Eigen değerlerini ve Eigen vektörlerini döndürür.
Aşağıdaki örneği ele alalım.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the eig function
l, v = linalg.eig(A)
#printing the result for eigen values
print l
#printing the result for eigen vectors
print vYukarıdaki program aşağıdaki çıktıyı üretecektir.
array([-0.37228132+0.j, 5.37228132+0.j]) #--Eigen Values
array([[-0.82456484, -0.41597356], #--Eigen Vectors
[ 0.56576746, -0.90937671]])Tekil Değer Ayrışımı
Tekil Değer Ayrıştırması (SVD), özdeğer probleminin kare olmayan matrislere bir uzantısı olarak düşünülebilir.
scipy.linalg.svd 'a' matrisini iki üniter matris 'U' ve 'Vh' ve tekil değerlerin (gerçek, negatif olmayan) bir 1-D dizisi 's' şeklinde çarpanlara ayırır, öyle ki a == U * S * Vh, burada 'S ', ana köşegen' s 'ile uygun şekilli bir sıfır matrisidir.
Aşağıdaki örneği ele alalım.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
a = np.random.randn(3, 2) + 1.j*np.random.randn(3, 2)
#Passing the values to the eig function
U, s, Vh = linalg.svd(a)
# printing the result
print U, Vh, sYukarıdaki program aşağıdaki çıktıyı üretecektir.
(
array([
[ 0.54828424-0.23329795j, -0.38465728+0.01566714j,
-0.18764355+0.67936712j],
[-0.27123194-0.5327436j , -0.57080163-0.00266155j,
-0.39868941-0.39729416j],
[ 0.34443818+0.4110186j , -0.47972716+0.54390586j,
0.25028608-0.35186815j]
]),
array([ 3.25745379, 1.16150607]),
array([
[-0.35312444+0.j , 0.32400401+0.87768134j],
[-0.93557636+0.j , -0.12229224-0.33127251j]
])
)SciPy ndimage alt modülü, görüntü işlemeye adanmıştır. Burada ndimage, n boyutlu görüntü anlamına gelir.
Görüntü işlemede en yaygın görevlerden bazıları aşağıdaki gibidir & miuns;
- Giriş / Çıkış, görüntüleri görüntüleme
- Temel manipülasyonlar - Kırpma, çevirme, döndürme vb.
- Görüntü filtreleme - Parazit giderme, keskinleştirme vb.
- Görüntü segmentasyonu - Farklı nesnelere karşılık gelen pikselleri etiketleme
- Classification
- Özellik çıkarma
- Registration
SciPy kullanılarak bunlardan bazılarının nasıl elde edilebileceğini tartışalım.
Görüntü Dosyalarını Açma ve Yazma
misc packageSciPy'de bazı resimlerle birlikte gelir. Bu görüntüleri, görüntü işlemlerini öğrenmek için kullanıyoruz. Aşağıdaki örneği ele alalım.
from scipy import misc
f = misc.face()
misc.imsave('face.png', f) # uses the Image module (PIL)
import matplotlib.pyplot as plt
plt.imshow(f)
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.

Ham biçimindeki herhangi bir görüntü, matris biçimindeki sayılarla temsil edilen renklerin birleşimidir. Bir makine, görüntüleri yalnızca bu sayılara göre anlar ve işler. RGB, popüler bir temsil yöntemidir.
Yukarıdaki görselin istatistiki bilgilerine bakalım.
from scipy import misc
face = misc.face(gray = False)
print face.mean(), face.max(), face.min()Yukarıdaki program aşağıdaki çıktıyı üretecektir.
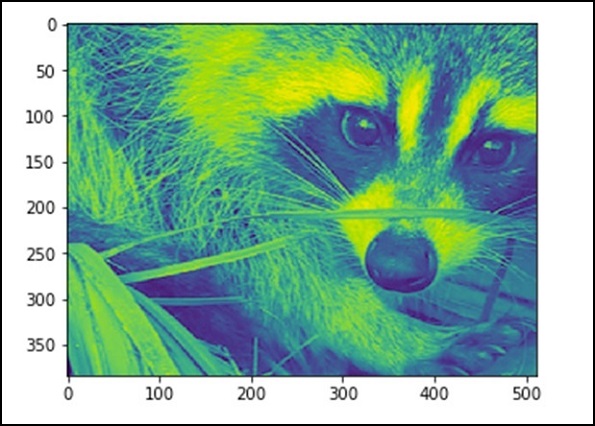
110.16274388631184, 255, 0Şimdi, görüntünün sayılardan oluştuğunu biliyoruz, bu nedenle sayının değerindeki herhangi bir değişiklik orijinal görüntüyü değiştirir. Görüntü üzerinde bazı geometrik dönüşümler yapalım. Temel geometrik işlem kırpmadır
from scipy import misc
face = misc.face(gray = True)
lx, ly = face.shape
# Cropping
crop_face = face[lx / 4: - lx / 4, ly / 4: - ly / 4]
import matplotlib.pyplot as plt
plt.imshow(crop_face)
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.
Görüntüyü ters çevirmek gibi bazı temel işlemleri de aşağıda anlatıldığı gibi gerçekleştirebiliriz.
# up <-> down flip
from scipy import misc
face = misc.face()
flip_ud_face = np.flipud(face)
import matplotlib.pyplot as plt
plt.imshow(flip_ud_face)
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.

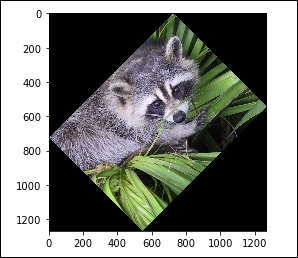
Bunun yanında bizde rotate() function, resmi belirli bir açıyla döndürür.
# rotation
from scipy import misc,ndimage
face = misc.face()
rotate_face = ndimage.rotate(face, 45)
import matplotlib.pyplot as plt
plt.imshow(rotate_face)
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.
Filtreler
Görüntü işlemede filtrelerin nasıl yardımcı olduğunu tartışalım.
Görüntü işlemede filtreleme nedir?
Filtreleme, bir görüntüyü değiştirmek veya geliştirmek için kullanılan bir tekniktir. Örneğin, belirli özellikleri vurgulamak veya diğer özellikleri kaldırmak için bir görüntüyü filtreleyebilirsiniz. Filtreleme ile uygulanan görüntü işleme işlemleri arasında Yumuşatma, Keskinleştirme ve Kenar İyileştirme bulunur.
Filtreleme, çıktı görüntüsündeki herhangi bir pikselin değerinin, karşılık gelen girdi pikselinin komşuluğundaki piksel değerlerine bazı algoritmalar uygulanarak belirlendiği bir komşuluk işlemidir. Şimdi SciPy ndimage kullanarak birkaç işlem yapalım.
Bulanıklaştırma
Görüntüdeki gürültüyü azaltmak için yaygın olarak bulanıklaştırma kullanılır. Bir filtre işlemi yapıp görseldeki değişimi görebiliriz. Aşağıdaki örneği ele alalım.
from scipy import misc
face = misc.face()
blurred_face = ndimage.gaussian_filter(face, sigma=3)
import matplotlib.pyplot as plt
plt.imshow(blurred_face)
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.

Sigma değeri, beşlik bir ölçekte bulanıklık seviyesini gösterir. Sigma değerini ayarlayarak görüntü kalitesindeki değişikliği görebiliriz. Bulanıklaştırma hakkında daha fazla ayrıntı için, → DIP (Dijital Görüntü İşleme) Eğitimi üzerine tıklayın.
Kenar algılama
Görüntü işlemede kenar algılamanın nasıl yardımcı olduğunu tartışalım.
Kenar Algılama nedir?
Kenar algılama, görüntülerdeki nesnelerin sınırlarını bulmaya yönelik bir görüntü işleme tekniğidir. Parlaklıktaki süreksizlikleri tespit ederek çalışır. Kenar algılama, Görüntü İşleme, Bilgisayarla Görme ve Makine Görüşü gibi alanlarda görüntü bölümleme ve veri çıkarma için kullanılır.
En yaygın kullanılan kenar algılama algoritmaları şunları içerir:
- Sobel
- Canny
- Prewitt
- Roberts
- Bulanık Mantık yöntemleri
Aşağıdaki örneği ele alalım.
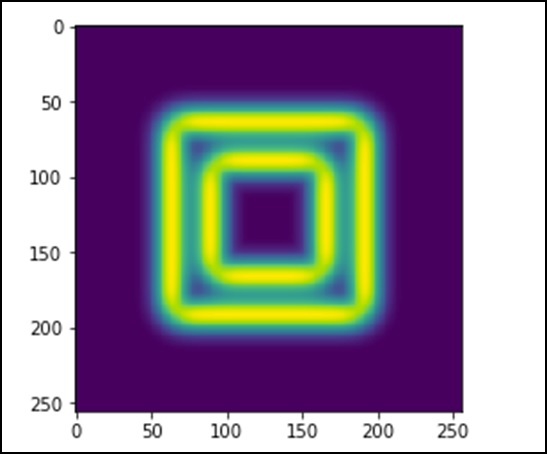
import scipy.ndimage as nd
import numpy as np
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
import matplotlib.pyplot as plt
plt.imshow(im)
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.

Görüntü kare bir renk bloğuna benziyor. Şimdi bu renkli blokların kenarlarını tespit edeceğiz. Burada ndimage,SobelBu işlemi gerçekleştirmek için. NumPy iseHypot sonuçtaki iki matrisi bire birleştirme işlevi.
Aşağıdaki örneği ele alalım.
import scipy.ndimage as nd
import matplotlib.pyplot as plt
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
sx = ndimage.sobel(im, axis = 0, mode = 'constant')
sy = ndimage.sobel(im, axis = 1, mode = 'constant')
sob = np.hypot(sx, sy)
plt.imshow(sob)
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.
scipy.optimize packageyaygın olarak kullanılan birkaç optimizasyon algoritması sağlar. Bu modül aşağıdaki yönleri içerir -
Çeşitli algoritmalar (örn. BFGS, Nelder-Mead simplex, Newton Conjugate Gradient, COBYLA veya SLSQP) kullanarak çok değişkenli skaler fonksiyonların kısıtlanmamış ve kısıtlı en aza indirilmesi (minimize ())
Küresel (kaba kuvvet) optimizasyon rutinleri (ör., Tavlama (), havzalama ())
En küçük kareler küçültme (leastsq ()) ve eğri uydurma (curve_fit ()) algoritmaları
Skaler tek değişkenli fonksiyon küçültme araçları (minimize_scalar ()) ve kök bulucular (newton ())
Çeşitli algoritmalar (örn. Hibrit Powell, Levenberg-Marquardt veya Newton-Krylov gibi büyük ölçekli yöntemler) kullanan çok değişkenli denklem sistemi çözücüleri (root ())
Çok değişkenli skaler fonksiyonların kısıtsız ve Kısıtlı minimizasyonu
minimize() function çok değişkenli skaler fonksiyonlar için kısıtlanmamış ve kısıtlı minimizasyon algoritmalarına ortak bir arayüz sağlar. scipy.optimize. Küçültme işlevini göstermek için, NN değişkenlerinin Rosenbrock işlevini küçültme sorununu düşünün -
$$f(x) = \sum_{i = 1}^{N-1} \:100(x_i - x_{i-1}^{2})$$
Bu işlevin minimum değeri 0'dır ve xi = 1 olduğunda elde edilir.
Nelder – Mead Simpleks Algoritması
Aşağıdaki örnekte, minimize () rutini, Nelder-Mead simplex algorithm (method = 'Nelder-Mead')(yöntem parametresi ile seçilir). Aşağıdaki örneği ele alalım.
import numpy as np
from scipy.optimize import minimize
def rosen(x):
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead')
print(res.x)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
[7.93700741e+54 -5.41692163e+53 6.28769150e+53 1.38050484e+55 -4.14751333e+54]Tek yönlü algoritma, oldukça iyi davranılmış bir işlevi en aza indirmenin muhtemelen en basit yoludur. Yalnızca işlev değerlendirmelerini gerektirir ve basit küçültme problemleri için iyi bir seçimdir. Bununla birlikte, herhangi bir gradyan değerlendirmesi kullanmadığı için minimum değeri bulmak daha uzun sürebilir.
Minimum değeri bulmak için yalnızca işlev çağrılarına ihtiyaç duyan başka bir optimizasyon algoritması, Powell‘s method, minimize () işlevinde method = 'powell' ayarlanarak kullanılabilir.
En Küçük Kareler
Doğrusal olmayan en küçük kareler problemini değişkenlerin sınırları ile çözün. Kalıntılar f (x) (n gerçek değişkenin m boyutlu bir gerçek fonksiyonu) ve kayıp fonksiyonu rho (s) (bir skaler fonksiyon) verildiğinde, en küçük kareler maliyet fonksiyonu F (x) için yerel bir minimum bulur. Aşağıdaki örneği ele alalım.
Bu örnekte, bağımsız değişkenler üzerinde sınırlar olmaksızın minimum Rosenbrock işlevi bulduk.
#Rosenbrock Function
def fun_rosenbrock(x):
return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
from scipy.optimize import least_squares
input = np.array([2, 2])
res = least_squares(fun_rosenbrock, input)
print resDikkat edin, biz sadece kalıntıların vektörünü sağlarız. Algoritma, maliyet işlevini, Rosenbrock işlevini veren artıkların karelerinin toplamı olarak oluşturur. Kesin minimum, x = [1.0,1.0] 'dır.
Yukarıdaki program aşağıdaki çıktıyı üretecektir.
active_mask: array([ 0., 0.])
cost: 9.8669242910846867e-30
fun: array([ 4.44089210e-15, 1.11022302e-16])
grad: array([ -8.89288649e-14, 4.44089210e-14])
jac: array([[-20.00000015,10.],[ -1.,0.]])
message: '`gtol` termination condition is satisfied.'
nfev: 3
njev: 3
optimality: 8.8928864934219529e-14
status: 1
success: True
x: array([ 1., 1.])Kök bulma
SciPy'de kök bulmanın nasıl yardımcı olduğunu anlayalım.
Skaler fonksiyonlar
Birinin tek değişkenli bir denklemi varsa, denenebilecek dört farklı kök bulma algoritması vardır. Bu algoritmaların her biri, bir kökün beklendiği bir aralığın uç noktalarını gerektirir (çünkü işlev işaretleri değiştirir). Genel olarak,brentq en iyi seçimdir, ancak diğer yöntemler belirli durumlarda veya akademik amaçlar için yararlı olabilir.
Sabit nokta çözme
Bir fonksiyonun sıfırlarını bulmakla yakından ilgili bir problem, bir fonksiyonun sabit bir noktasını bulma problemidir. Bir fonksiyonun sabit noktası, fonksiyonun değerlendirilmesinin şu noktayı döndürdüğü noktadır: g (x) = x. Açıkça sabit noktaggf (x) = g (x) −x'in köküdür. Aynı şekilde, köküffg (x) = f (x) + x'in sabit_ noktasıdır. Sabit nokta rutin, basit bir yinelemeli yöntem sağlar.Aitkens sequence acceleration sabit noktasını tahmin etmek gg, bir başlangıç noktası verilirse.
Denklem setleri
Doğrusal olmayan denklemler kümesinin kökünü bulmak, root() function. Aralarında birkaç yöntem mevcutturhybr (varsayılan) ve lm, sırasıyla hybrid method of Powell ve Levenberg-Marquardt method MINPACK'ten.
Aşağıdaki örnek, tek değişkenli transandantal denklemi ele almaktadır.
x2 + 2cos(x) = 0
Kökü aşağıdaki gibi bulunabilir -
import numpy as np
from scipy.optimize import root
def func(x):
return x*2 + 2 * np.cos(x)
sol = root(func, 0.3)
print solYukarıdaki program aşağıdaki çıktıyı üretecektir.
fjac: array([[-1.]])
fun: array([ 2.22044605e-16])
message: 'The solution converged.'
nfev: 10
qtf: array([ -2.77644574e-12])
r: array([-3.34722409])
status: 1
success: True
x: array([-0.73908513])Tüm istatistik fonksiyonları alt pakette bulunur scipy.stats ve bu işlevlerin oldukça eksiksiz bir listesi kullanılarak elde edilebilir info(stats)işlevi. Mevcut rasgele değişkenlerin bir listesi de şuradan elde edilebilir:docstringistatistikler alt paketi için. Bu modül, çok sayıda olasılık dağılımının yanı sıra büyüyen bir istatistiksel fonksiyonlar kütüphanesi içerir.
Her tek değişkenli dağıtım, aşağıdaki tabloda açıklandığı gibi kendi alt sınıfına sahiptir -
| Sr. No. | Sınıf ve Açıklama |
|---|---|
| 1 | rv_continuous Alt sınıflandırma için kullanılan genel bir sürekli rastgele değişken sınıfı |
| 2 | rv_discrete Alt sınıflandırma için kullanılan genel bir ayrık rastgele değişken sınıfı |
| 3 | rv_histogram Histogram tarafından verilen bir dağılım oluşturur |
Normal Sürekli Rastgele Değişken
X rastgele değişkeninin herhangi bir değeri alabildiği bir olasılık dağılımı, sürekli rastgele değişkendir. Location (loc) anahtar sözcüğü ortalamayı belirtir. Ölçek (ölçek) anahtar sözcüğü standart sapmayı belirtir.
Bir örneği olarak rv_continuous sınıf, norm nesne, ondan bir genel yöntemler koleksiyonunu miras alır ve bunları bu belirli dağıtım için özel ayrıntılarla tamamlar.
CDF'yi birkaç noktada hesaplamak için bir liste veya NumPy dizisi geçirebiliriz. Aşağıdaki örneği ele alalım.
from scipy.stats import norm
import numpy as np
print norm.cdf(np.array([1,-1., 0, 1, 3, 4, -2, 6]))Yukarıdaki program aşağıdaki çıktıyı üretecektir.
array([ 0.84134475, 0.15865525, 0.5 , 0.84134475, 0.9986501 ,
0.99996833, 0.02275013, 1. ])Bir dağılımın medyanını bulmak için, CDF'nin tersi olan Yüzde Nokta Fonksiyonunu (PPF) kullanabiliriz. Aşağıdaki örneği kullanarak anlayalım.
from scipy.stats import norm
print norm.ppf(0.5)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
0.0Bir rastgele değişken dizisi oluşturmak için aşağıdaki örnekte gösterilen boyut anahtar kelime argümanını kullanmalıyız.
from scipy.stats import norm
print norm.rvs(size = 5)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
array([ 0.20929928, -1.91049255, 0.41264672, -0.7135557 , -0.03833048])Yukarıdaki çıktı yeniden üretilemez. Aynı rastgele sayıları üretmek için tohum işlevini kullanın.
Üniforma dağıtımı
Tekdüze fonksiyon kullanılarak düzgün bir dağılım oluşturulabilir. Aşağıdaki örneği ele alalım.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])Ayrık Dağıtım Oluşturun
Rastgele bir örnek oluşturalım ve gözlemlenen frekansları olasılıklarla karşılaştıralım.
Binom dağılımı
Bir örneği olarak rv_discrete class, binom objectondan bir genel yöntemler koleksiyonunu miras alır ve bunları bu belirli dağıtım için özel ayrıntılarla tamamlar. Aşağıdaki örneği ele alalım.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])Tanımlayıcı istatistikler
Min, Maks, Ortalama ve Varyans gibi temel istatistikler NumPy dizisini girdi olarak alır ve ilgili sonuçları döndürür. İçinde bulunan birkaç temel istatistiksel fonksiyonscipy.stats package aşağıdaki tabloda açıklanmaktadır.
| Sr. No. | İşlev ve Açıklama |
|---|---|
| 1 | describe() Aktarılan dizinin birkaç tanımlayıcı istatistiğini hesaplar |
| 2 | gmean() Belirtilen eksen boyunca geometrik ortalamayı hesaplar |
| 3 | hmean() Belirtilen eksen boyunca harmonik ortalamayı hesaplar |
| 4 | kurtosis() Basıklığı hesaplar |
| 5 | mode() Modal değeri verir |
| 6 | skew() Verinin çarpıklığını test eder |
| 7 | f_oneway() 1 yönlü ANOVA gerçekleştirir |
| 8 | iqr() Verinin çeyrekler arası aralığını belirtilen eksen boyunca hesaplar |
| 9 | zscore() Örnek ortalamasına ve standart sapmaya göre örnekteki her bir değerin z puanını hesaplar |
| 10 | sem() Giriş dizisindeki değerlerin ortalamasının (veya standart ölçüm hatasını) standart hatasını hesaplar |
Bu işlevlerin birçoğunun, scipy.stats.mstats, maskelenmiş diziler için çalışır. Bunu aşağıda verilen örnekle anlayalım.
from scipy import stats
import numpy as np
x = np.array([1,2,3,4,5,6,7,8,9])
print x.max(),x.min(),x.mean(),x.var()Yukarıdaki program aşağıdaki çıktıyı üretecektir.
(9, 1, 5.0, 6.666666666666667)T testi
SciPy'de T-test'in nasıl yararlı olduğunu anlayalım.
ttest_1samp
BİR puan grubunun ortalaması için T testini hesaplar. Bu, bağımsız gözlemler 'a' örneğinin beklenen değerinin (ortalama) verilen popülasyon ortalamasına eşit olduğu boş hipotezi için iki taraflı bir testtir,popmean. Aşağıdaki örneği ele alalım.
from scipy import stats
rvs = stats.norm.rvs(loc = 5, scale = 10, size = (50,2))
print stats.ttest_1samp(rvs,5.0)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
Ttest_1sampResult(statistic = array([-1.40184894, 2.70158009]),
pvalue = array([ 0.16726344, 0.00945234]))İki numunenin karşılaştırılması
Aşağıdaki örneklerde, aynı veya farklı dağılımdan gelebilecek iki örnek vardır ve bu örneklerin aynı istatistiksel özelliklere sahip olup olmadığını test etmek istiyoruz.
ttest_ind- İki bağımsız puan örnekleminin ortalamaları için T testini hesaplar. Bu, iki bağımsız örneğin aynı ortalama (beklenen) değerlere sahip olduğuna dair sıfır hipotezi için iki taraflı bir testtir. Bu test, popülasyonların varsayılan olarak aynı varyanslara sahip olduğunu varsayar.
Aynı veya farklı popülasyondan iki bağımsız örnek gözlemlersek bu testi kullanabiliriz. Aşağıdaki örneği ele alalım.
from scipy import stats
rvs1 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
rvs2 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
print stats.ttest_ind(rvs1,rvs2)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
Ttest_indResult(statistic = -0.67406312233650278, pvalue = 0.50042727502272966)Aynısını, aynı uzunlukta, ancak farklı bir ortalama ile yeni bir dizi ile test edebilirsiniz. İçinde farklı bir değer kullanınloc ve aynısını test edin.
CSGraph'ın açılımı Compressed Sparse Graph, seyrek matris gösterimlerine dayalı Hızlı grafik algoritmalarına odaklanan.
Grafik Gösterimleri
Başlangıç olarak, seyrek grafiğin ne olduğunu ve grafik gösterimlerine nasıl yardımcı olduğunu anlayalım.
Seyrek grafik tam olarak nedir?
Grafik, aralarında bağlantıları olan bir düğümler koleksiyonudur. Grafikler neredeyse her şeyi temsil edebilir - her düğümün bir kişi olduğu ve tanıdıklarla bağlantılı olduğu sosyal ağ bağlantıları; her düğümün bir piksel olduğu ve komşu piksellere bağlandığı görüntüler; her bir düğümün en yakın komşularına bağlandığı yüksek boyutlu bir dağılımdaki noktalar; ve hemen hemen hayal edebileceğiniz her şey.
Grafik verilerini göstermenin çok etkili bir yolu, seyrek bir matristedir: buna G diyelim. Matris G, N x N boyutundadır ve G [i, j], 'i' düğümü ile düğüm arasındaki bağlantının değerini verir. 'j'. Seyrek bir grafik çoğunlukla sıfır içerir - yani, çoğu düğümün yalnızca birkaç bağlantısı vardır. Bu özelliğin çoğu ilgi durumunda doğru olduğu ortaya çıkar.
Seyrek grafik alt modülünün oluşturulması, aşağıdakileri içeren scikit-learn'de kullanılan çeşitli algoritmalar tarafından motive edildi -
Isomap - Bir grafikteki en kısa yolları bulmayı gerektiren çok katlı bir öğrenme algoritması.
Hierarchical clustering - Minimum yayılma ağacına dayalı bir kümeleme algoritması.
Spectral Decomposition - Seyrek grafik laplacians tabanlı bir projeksiyon algoritması.
Somut bir örnek olarak, aşağıdaki yönsüz grafiği temsil etmek istediğimizi hayal edin -
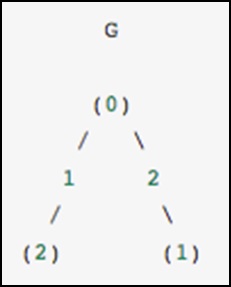
Bu grafikte, düğüm 0 ve 1'in 2 ağırlık kenarıyla ve 0 ve 2 düğümlerinin 1 ağırlık kenarıyla bağlandığı üç düğüm vardır. Aşağıdaki örnekte gösterildiği gibi yoğun, maskelenmiş ve seyrek gösterimleri oluşturabiliriz. yönsüz bir grafiğin simetrik bir matris ile temsil edildiğini akılda tutarak.
G_dense = np.array([ [0, 2, 1],
[2, 0, 0],
[1, 0, 0] ])
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix
G_sparse = csr_matrix(G_dense)
print G_sparse.dataYukarıdaki program aşağıdaki çıktıyı üretecektir.
array([2, 1, 2, 1])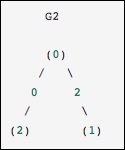
Bu, 0 ve 2 numaralı düğümlerin sıfır ağırlıklı bir kenarla bağlanması dışında önceki grafikle aynıdır. Bu durumda, yukarıdaki yoğun gösterim belirsizliklere yol açar - sıfır anlamlı bir değer ise kenar olmayanlar nasıl temsil edilebilir. Bu durumda belirsizliği ortadan kaldırmak için ya maskelenmiş ya da seyrek bir temsil kullanılmalıdır.
Aşağıdaki örneği ele alalım.
from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
[np.inf, 2, 0 ],
[2, np.inf, np.inf],
[0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.dataYukarıdaki program aşağıdaki çıktıyı üretecektir.
array([ 2., 0., 2., 0.])Seyrek grafikler kullanan kelime merdivenleri
Kelime merdivenleri, Lewis Carroll tarafından icat edilen ve kelimelerin her adımda tek bir harf değiştirilerek birbirine bağlandığı bir oyundur. Örneğin -
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
Burada, yedi adımda "APE" den "MAN" e geçtik ve her seferinde bir harf değiştirdik. Soru şu: Aynı kuralı kullanarak bu kelimeler arasında daha kısa bir yol bulabilir miyiz? Bu problem doğal olarak seyrek grafik problemi olarak ifade edilir. Düğümler tek tek kelimelere karşılık gelecek ve en çok bir harf farklı olan kelimeler arasında bağlantılar oluşturacağız.
Bir Sözcük Listesi Elde Etme
İlk olarak, tabii ki, geçerli kelimelerin bir listesini elde etmeliyiz. Mac çalıştırıyorum ve Mac'in aşağıdaki kod bloğunda verilen konumda bir kelime sözlüğü var. Farklı bir mimaride iseniz, sistem sözlüğünüzü bulmak için biraz aramanız gerekebilir.
wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
235886Şimdi 3 uzunluğundaki kelimelere bakmak istiyoruz, bu yüzden sadece doğru uzunluktaki kelimeleri seçelim. Büyük harfle (özel isimler) başlayan veya kesme işareti ve kısa çizgi gibi alfa sayısal olmayan karakterler içeren sözcükleri de eleyeceğiz. Son olarak, daha sonra karşılaştırma yapmak için her şeyin küçük harf olmasını sağlayacağız.
word_list = [word for word in word_list if len(word) == 3]
word_list = [word for word in word_list if word[0].islower()]
word_list = [word for word in word_list if word.isalpha()]
word_list = map(str.lower, word_list)
print len(word_list)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
1135Şimdi, 1135 geçerli üç harfli kelimeden oluşan bir listemiz var (tam sayı kullanılan belirli listeye bağlı olarak değişebilir). Bu kelimelerin her biri grafiğimizde bir düğüm olacak ve her kelime çiftiyle ilişkili düğümleri birbirine bağlayan, yalnızca bir harf farklı olan kenarlar oluşturacağız.
import numpy as np
word_list = np.asarray(word_list)
word_list.dtype
word_list.sort()
word_bytes = np.ndarray((word_list.size, word_list.itemsize),
dtype = 'int8',
buffer = word_list.data)
print word_bytes.shapeYukarıdaki program aşağıdaki çıktıyı üretecektir.
(1135, 3)Hangi kelime çiftlerinin bağlı olduğunu belirlemek için her nokta arasındaki Hamming mesafesini kullanacağız. Hamming mesafesi, farklı olan iki vektör arasındaki girişlerin fraksiyonunu ölçer: 1 / N1 / N'ye eşit hamming mesafesine sahip herhangi iki kelime, burada NN, kelime merdivenine bağlı harflerin sayısıdır.
from scipy.spatial.distance import pdist, squareform
from scipy.sparse import csr_matrix
hamming_dist = pdist(word_bytes, metric = 'hamming')
graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))Mesafeleri karşılaştırırken eşitlik kullanmayız çünkü bu, kayan nokta değerleri için kararsız olabilir. Eşitsizlik, kelime listesindeki iki giriş aynı olmadığı sürece istenen sonucu üretir. Artık grafiğimiz ayarlandığına göre, grafikteki herhangi iki kelime arasındaki yolu bulmak için en kısa yol aramasını kullanacağız.
i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]Yukarıdaki program aşağıdaki çıktıyı üretecektir.
ape, manBunların eşleşip eşleşmediğini kontrol etmemiz gerekiyor, çünkü eğer kelimeler listede yoksa çıktıda bir hata olacaktır. Şimdi tek ihtiyacımız olan grafikteki bu iki indeks arasındaki en kısa yolu bulmak. Kullanacağızdijkstra’s algoritması, çünkü sadece bir düğümün yolunu bulmamıza izin veriyor.
from scipy.sparse.csgraph import dijkstra
distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True)
print distances[i2]Yukarıdaki program aşağıdaki çıktıyı üretecektir.
5.0Böylece 'maymun' ve 'insan' arasındaki en kısa yolun sadece beş basamaktan oluştuğunu görüyoruz. Bu yolu yeniden yapılandırmak için algoritma tarafından döndürülen öncülleri kullanabiliriz.
path = []
i = i2
while i != i1:
path.append(word_list[i])
i = predecessors[i]
path.append(word_list[i1])
print path[::-1]i2]Yukarıdaki program aşağıdaki çıktıyı üretecektir.
['ape', 'ope', 'opt', 'oat', 'mat', 'man']scipy.spatial package bir dizi noktanın Üçgenleşmelerini, Voronoi Diyagramlarını ve Dışbükey Gövdelerini, Qhull library. Üstelik içerirKDTree implementations en yakın komşu nokta sorguları ve çeşitli ölçülerdeki mesafe hesaplamaları için yardımcı programlar için.
Delaunay Üçgenlemeleri
Delaunay Triangülasyonlarının ne olduğunu ve SciPy'de nasıl kullanıldığını anlayalım.
Delaunay Üçgenlemeleri nedir?
Matematik ve hesaplamalı geometride, belirli bir küme için bir Delaunay üçgenlemesi P bir düzlemdeki ayrık noktaların sayısı bir üçgenlemedir DT(P) öyle ki anlamı yok P DT (P) 'deki herhangi bir üçgenin çemberinin içindedir.
Aynı şeyi SciPy aracılığıyla da hesaplayabiliriz. Aşağıdaki örneği ele alalım.
from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.

Eşdüzlem Noktaları
Coplanar Puanlarının ne olduğunu ve SciPy'de nasıl kullanıldığını anlayalım.
Eşdüzlem Puanları nelerdir?
Eş düzlemli noktalar, aynı düzlemde bulunan üç veya daha fazla noktadır. Bir düzlemin her yöne uçsuz bucaksız uzanan düz bir yüzey olduğunu hatırlayın. Genellikle matematik ders kitaplarında dört kenarlı bir şekil olarak gösterilir.
SciPy kullanarak bunu nasıl bulabileceğimize bir bakalım. Aşağıdaki örneği ele alalım.
from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanarYukarıdaki program aşağıdaki çıktıyı üretecektir.
array([[4, 0, 3]], dtype = int32)Bu, nokta 4'ün üçgen 0 ve tepe 3'ün yakınında bulunduğu, ancak üçgenlemeye dahil olmadığı anlamına gelir.
Dışbükey gövdeler
Dışbükey gövdelerin ne olduğunu ve SciPy'de nasıl kullanıldığını anlayalım.
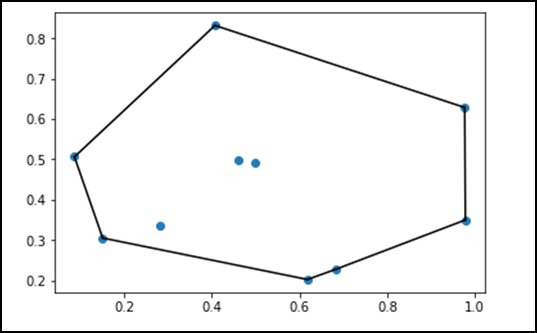
Konveks Kabuklar nedir?
Matematikte convex hull veya convex envelope Öklid düzlemindeki veya bir Öklid uzayındaki (veya daha genel olarak, gerçekler üzerindeki afin boşluktaki) X noktalarının en küçük convex set X.
Ayrıntılı olarak anlamak için aşağıdaki örneği ele alalım.
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()Yukarıdaki program aşağıdaki çıktıyı üretecektir.
ODR, Orthogonal Distance Regressionregresyon çalışmalarında kullanılan. Temel doğrusal regresyon genellikle iki değişken arasındaki ilişkiyi tahmin etmek için kullanılıry ve x grafiğe en uygun çizgiyi çizerek.
Bunun için kullanılan matematiksel yöntem olarak bilinir Least Squaresve her nokta için hata karesinin toplamını en aza indirmeyi amaçlamaktadır. Buradaki kilit soru, her nokta için hatayı (artık olarak da bilinir) nasıl hesaplayacağınızdır?
Standart bir doğrusal regresyonda amaç, X değerinden Y değerini tahmin etmektir - bu nedenle yapılacak mantıklı şey Y değerlerindeki hatayı hesaplamaktır (aşağıdaki görüntüde gri çizgiler olarak gösterilmiştir). Bununla birlikte, bazen hem X hem de Y'deki hatayı hesaba katmak daha mantıklıdır (aşağıdaki görüntüde noktalı kırmızı çizgilerle gösterildiği gibi).
Örneğin - X ölçümlerinizin belirsiz olduğunu bildiğinizde veya bir değişkenin diğerine göre hatalarına odaklanmak istemediğinizde.
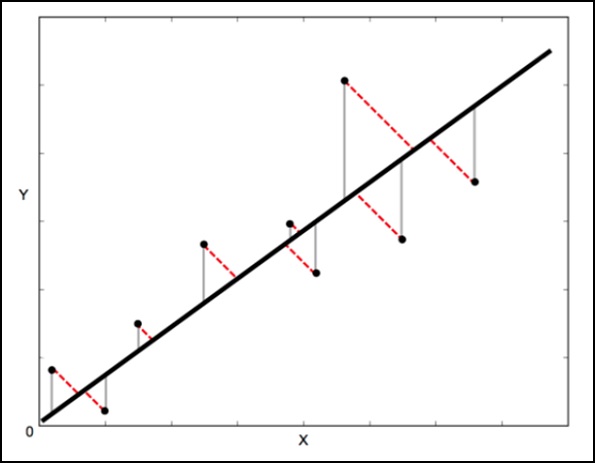
Ortogonal Mesafe Regresyonu (ODR), bunu yapabilen bir yöntemdir (bu bağlamda ortogonal, dikey anlamına gelir - bu nedenle, hataları 'dikey olarak' değil, hatta dikey olarak hesaplar).
Tek Değişkenli Regresyon için scipy.odr Uygulaması
Aşağıdaki örnek, tek değişkenli regresyon için scipy.odr uygulamasını gösterir.
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])
# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
m, c = p
return m*x + c
# Create a model for fitting.
linear_model = Model(linear_func)
# Create a RealData object using our initiated data from above.
data = RealData(x, y)
# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])
# Run the regression.
out = odr.run()
# Use the in-built pprint method to give us results.
out.pprint()Yukarıdaki program aşağıdaki çıktıyı üretecektir.
Beta: [ 5.51846098 -4.25744878]
Beta Std Error: [ 0.7786442 2.33126407]
Beta Covariance: [
[ 1.93150969 -4.82877433]
[ -4.82877433 17.31417201
]]
Residual Variance: 0.313892697582
Inverse Condition #: 0.146618499389
Reason(s) for Halting:
Sum of squares convergenceÖzel pakette bulunan işlevler, yayın ve otomatik dizi döngüsünü takip eden evrensel işlevlerdir.
En sık kullanılan özel işlevlerden bazılarına bakalım -
- Kübik Kök Fonksiyonu
- Üstel Fonksiyon
- Bağıl Hata Üstel Fonksiyon
- Günlük Toplamı Üstel İşlevi
- Lambert İşlevi
- Permütasyonlar ve Kombinasyonlar İşlevi
- Gama İşlevi
Şimdi bu işlevlerin her birini kısaca anlayalım.
Kübik Kök Fonksiyonu
Bu kübik kök işlevinin sözdizimi - scipy.special.cbrt (x) şeklindedir. Bu, öğenin element-bilge küp kökünü getirecektir.x.
Aşağıdaki örneği ele alalım.
from scipy.special import cbrt
res = cbrt([10, 9, 0.1254, 234])
print resYukarıdaki program aşağıdaki çıktıyı üretecektir.
[ 2.15443469 2.08008382 0.50053277 6.16224015]Üstel Fonksiyon
Üstel işlevin sözdizimi - scipy.special.exp10 (x) şeklindedir. Bu, 10 ** x elemanını hesaplayacaktır.
Aşağıdaki örneği ele alalım.
from scipy.special import exp10
res = exp10([2, 9])
print resYukarıdaki program aşağıdaki çıktıyı üretecektir.
[1.00000000e+02 1.00000000e+09]Bağıl Hata Üstel Fonksiyon
Bu işlevin sözdizimi - scipy.special.exprel (x) şeklindedir. Göreceli üstel hatası üretir, (exp (x) - 1) / x.
Ne zaman xsıfıra yakın, exp (x) 1'e yakın, bu nedenle exp (x) - 1'in sayısal hesaplaması felaket bir hassasiyet kaybına neden olabilir. Ardından, hassasiyet kaybını önlemek için exprel (x) uygulanır.x sıfıra yakın.
Aşağıdaki örneği ele alalım.
from scipy.special import exprel
res = exprel([-0.25, -0.1, 0, 0.1, 0.25])
print resYukarıdaki program aşağıdaki çıktıyı üretecektir.
[0.88479687 0.95162582 1. 1.05170918 1.13610167]Günlük Toplamı Üstel İşlevi
Bu işlevin sözdizimi - scipy.special.logsumexp (x) şeklindedir. Giriş öğelerinin üstel sayılarının toplamının günlüğünü hesaplamaya yardımcı olur.
Aşağıdaki örneği ele alalım.
from scipy.special import logsumexp
import numpy as np
a = np.arange(10)
res = logsumexp(a)
print resYukarıdaki program aşağıdaki çıktıyı üretecektir.
9.45862974443Lambert İşlevi
Bu işlevin sözdizimi - scipy.special.lambertw (x) şeklindedir. Lambert W işlevi olarak da adlandırılır. Lambert W fonksiyonu W (z), w * exp (w) 'nin ters fonksiyonu olarak tanımlanır. Başka bir deyişle, W (z) 'nin değeri, herhangi bir karmaşık sayı z için z = W (z) * exp (W (z)) olacak şekildedir.
Lambert W işlevi, sonsuz sayıda dal içeren çok değerli bir işlevdir. Her dal, z = w exp (w) denkleminin ayrı bir çözümünü verir. Burada dallar k tamsayısı ile indekslenir.
Aşağıdaki örneği ele alalım. Burada, Lambert W fonksiyonu w exp (w) 'nin tersidir.
from scipy.special import lambertw
w = lambertw(1)
print w
print w * np.exp(w)Yukarıdaki program aşağıdaki çıktıyı üretecektir.
(0.56714329041+0j)
(1+0j)Permütasyonlar ve Kombinasyonlar
Açıkça anlamak için permütasyonları ve kombinasyonları ayrı ayrı tartışalım.
Combinations- Kombinasyon işlevinin sözdizimi - scipy.special.comb (N, k) şeklindedir. Şu örneği ele alalım -
from scipy.special import comb
res = comb(10, 3, exact = False,repetition=True)
print resYukarıdaki program aşağıdaki çıktıyı üretecektir.
220.0Note- Dizi bağımsız değişkenleri yalnızca kesin = Yanlış durum için kabul edilir. K> N, N <0 veya k <0 ise, 0 döndürülür.
Permutations- Kombinasyon işlevinin sözdizimi - scipy.special.perm (N, k) şeklindedir. Bir seferde k alınan N şeylerin permütasyonları, yani N'nin k-permütasyonları. Bu aynı zamanda "kısmi permütasyonlar" olarak da bilinir.
Aşağıdaki örneği ele alalım.
from scipy.special import perm
res = perm(10, 3, exact = True)
print resYukarıdaki program aşağıdaki çıktıyı üretecektir.
720Gama İşlevi
Doğal bir sayı için z * gama (z) = gama (z + 1) ve gama (n + 1) = n! Olduğundan, gama işlevi genellikle genelleştirilmiş faktöriyel olarak adlandırılır.
Kombinasyon işlevinin sözdizimi - scipy.special.gamma (x) şeklindedir. Bir seferde k alınan N şeylerin permütasyonları, yani N'nin k-permütasyonları. Bu aynı zamanda "kısmi permütasyonlar" olarak da bilinir.
Kombinasyon işlevinin sözdizimi - scipy.special.gamma (x) şeklindedir. Bir seferde k alınan N şeylerin permütasyonları, yani N'nin k-permütasyonları. Bu aynı zamanda "kısmi permütasyonlar" olarak da bilinir.
from scipy.special import gamma
res = gamma([0, 0.5, 1, 5])
print resYukarıdaki program aşağıdaki çıktıyı üretecektir.
[inf 1.77245385 1. 24.]