TensorFlow - Matematiksel Temeller
TensorFlow'da temel uygulamayı oluşturmadan önce TensorFlow için gereken matematiksel kavramları anlamak önemlidir. Matematik, herhangi bir makine öğrenimi algoritmasının kalbi olarak kabul edilir. Matematiğin temel kavramlarının yardımıyla, belirli makine öğrenimi algoritması için bir çözüm tanımlanmıştır.
Vektör
Sürekli veya ayrı olan bir sayı dizisi vektör olarak tanımlanır. Makine öğrenimi algoritmaları, daha iyi çıktı üretimi için sabit uzunlukta vektörlerle ilgilenir.
Makine öğrenimi algoritmaları çok boyutlu verilerle ilgilenir, böylece vektörler çok önemli bir rol oynar.

Vektör modelinin resimli temsili aşağıda gösterildiği gibidir -
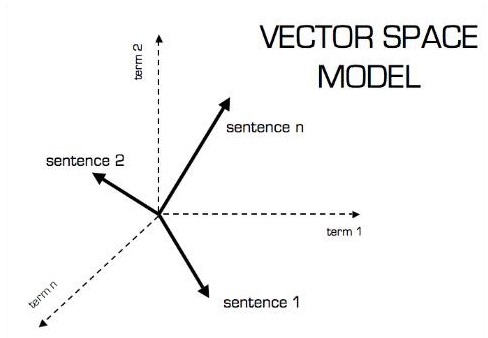
Skaler
Skaler, tek boyutlu vektör olarak tanımlanabilir. Skalarlar, yalnızca büyüklüğü içeren ve yön içermeyenlerdir. Skalerlerde sadece büyüklükle ilgileniyoruz.
Skaler örnekleri, çocukların ağırlık ve boy parametrelerini içerir.
Matris
Matris, satırlar ve sütunlar biçiminde düzenlenmiş çok boyutlu diziler olarak tanımlanabilir. Matrisin boyutu, satır uzunluğu ve sütun uzunluğu ile tanımlanır. Aşağıdaki şekil, belirli bir matrisin temsilini göstermektedir.
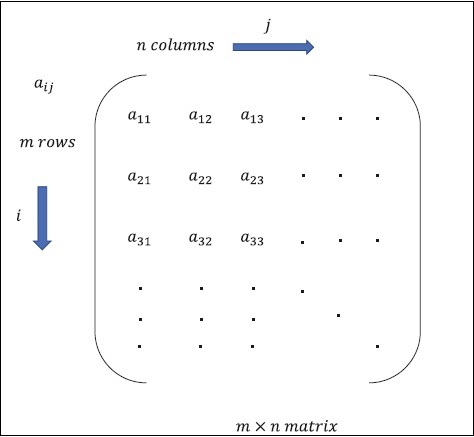
Yukarıda belirtildiği gibi “m” satırlı ve “n” sütunlu matrisi düşünün, matris gösterimi, matrisin uzunluğunu da tanımlayan “m * n matris” olarak belirtilecektir.
Matematiksel Hesaplamalar
Bu bölümde, TensorFlow'daki farklı Matematiksel Hesaplamalar hakkında bilgi edineceğiz.
Matrislerin eklenmesi
Matrisler aynı boyuttaysa iki veya daha fazla matrisin eklenmesi mümkündür. Ekleme, verilen konuma göre her elemanın eklenmesini ifade eder.
Matrislerin toplamasının nasıl çalıştığını anlamak için aşağıdaki örneği düşünün -
$$Example:A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:then\:A+B=\begin{bmatrix}1+5 & 2+6 \\3+7 & 4+8 \end{bmatrix}=\begin{bmatrix}6 & 8 \\10 & 12 \end{bmatrix}$$
Matrislerin çıkarılması
Matrislerin çıkarılması, iki matrisin toplanması gibi benzer şekilde çalışır. Kullanıcı, boyutların eşit olması koşuluyla iki matrisi çıkarabilir.
$$Example:A-\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B-\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:then\:A-B-\begin{bmatrix}1-5 & 2-6 \\3-7 & 4-8 \end{bmatrix}-\begin{bmatrix}-4 & -4 \\-4 & -4 \end{bmatrix}$$
Matrislerin çarpımı
A m * n ve B p * q matrislerinin çarpılabilir olması için, n eşit olmalıdır p. Ortaya çıkan matris -
C m * q
$$A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}$$
$$c_{11}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=1\times5+2\times7=19\:c_{12}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=1\times6+2\times8=22$$
$$c_{21}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=3\times5+4\times7=43\:c_{22}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=3\times6+4\times8=50$$
$$C=\begin{bmatrix}c_{11} & c_{12} \\c_{21} & c_{22} \end{bmatrix}=\begin{bmatrix}19 & 22 \\43 & 50 \end{bmatrix}$$
Matrisin devri
Bir A, m * n matrisinin devri genellikle AT (devrik) n * m ile temsil edilir ve sütun vektörlerinin sıra vektörleri olarak yer değiştirmesiyle elde edilir.
$$Example:A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}\:then\:A^{T}\begin{bmatrix}1 & 3 \\2 & 4 \end{bmatrix}$$
Vektörlerin nokta çarpımı
Herhangi bir n boyut vektörü, bir v = R ^ n * 1 matrisi olarak temsil edilebilir.
$$v_{1}=\begin{bmatrix}v_{11} \\v_{12} \\\cdot\\\cdot\\\cdot\\v_{1n}\end{bmatrix}v_{2}=\begin{bmatrix}v_{21} \\v_{22} \\\cdot\\\cdot\\\cdot\\v_{2n}\end{bmatrix}$$
İki vektörün iç çarpımı, karşılık gelen bileşenlerin çarpımının toplamıdır - Aynı boyuttaki bileşenler ve şu şekilde ifade edilebilir:
$$v_{1}\cdot v_{2}=v_1^Tv_{2}=v_2^Tv_{1}=v_{11}v_{21}+v_{12}v_{22}+\cdot\cdot+v_{1n}v_{2n}=\displaystyle\sum\limits_{k=1}^n v_{1k}v_{2k}$$
Vektörlerin nokta çarpımı örneği aşağıda belirtilmiştir -
$$Example:v_{1}=\begin{bmatrix}1 \\2 \\3\end{bmatrix}v_{2}=\begin{bmatrix}3 \\5 \\-1\end{bmatrix}v_{1}\cdot v_{2}=v_1^Tv_{2}=1\times3+2\times5-3\times1=10$$