AI - Các thuật toán tìm kiếm phổ biến
Tìm kiếm là kỹ thuật giải quyết vấn đề phổ biến trong AI. Có một số trò chơi một người chơi như trò chơi xếp hình, Sudoku, ô chữ, v.v. Các thuật toán tìm kiếm giúp bạn tìm kiếm một vị trí cụ thể trong các trò chơi đó.
Các vấn đề tìm kiếm tác nhân đơn lẻ
Các trò chơi như câu đố 3X3 tám ô, 4X4 mười lăm ô và 5X5 hai mươi bốn ô là những thử thách tìm đường cho một tác nhân. Chúng bao gồm một ma trận các ô với một ô trống. Người chơi được yêu cầu sắp xếp các ô bằng cách trượt một ô theo chiều dọc hoặc chiều ngang vào một khoảng trống với mục đích hoàn thành một số mục tiêu.
Các ví dụ khác về các bài toán tìm đường đại lý đơn lẻ là Bài toán người bán hàng đi du lịch, Khối lập phương Rubik và Chứng minh định lý.
Thuật ngữ Tìm kiếm
Problem Space- Đó là môi trường mà cuộc tìm kiếm diễn ra. (Một tập hợp các trạng thái và tập hợp các toán tử để thay đổi các trạng thái đó)
Problem Instance - Đó là Trạng thái ban đầu + Trạng thái mục tiêu.
Problem Space Graph- Nó thể hiện trạng thái vấn đề. Các trạng thái được hiển thị bằng các nút và các toán tử được hiển thị bằng các cạnh.
Depth of a problem - Độ dài của đường đi ngắn nhất hoặc chuỗi toán tử ngắn nhất từ Trạng thái ban đầu đến trạng thái mục tiêu.
Space Complexity - Số lượng nút tối đa được lưu trữ trong bộ nhớ.
Time Complexity - Số lượng nút tối đa được tạo.
Admissibility - Một tính chất của thuật toán để luôn tìm ra một giải pháp tối ưu.
Branching Factor - Số nút con trung bình trong đồ thị không gian bài toán.
Depth - Độ dài của đường đi ngắn nhất từ trạng thái ban đầu đến trạng thái mục tiêu.
Chiến lược tìm kiếm Brute-Force
Chúng đơn giản nhất, vì chúng không cần bất kỳ kiến thức nào về miền cụ thể. Chúng hoạt động tốt với một số trạng thái có thể có.
Yêu cầu -
- Mô tả trạng thái
- Một tập hợp các toán tử hợp lệ
- Trạng thái ban đầu
- Mô tả trạng thái mục tiêu
Breadth-First Search
Nó bắt đầu từ nút gốc, khám phá các nút lân cận trước và chuyển sang các nút lân cận cấp độ tiếp theo. Nó tạo ra từng cây một cho đến khi tìm ra giải pháp. Nó có thể được thực hiện bằng cách sử dụng cấu trúc dữ liệu hàng đợi FIFO. Phương pháp này cung cấp đường dẫn ngắn nhất đến giải pháp.
Nếu branching factor(số nút con trung bình của một nút nhất định) = b và độ sâu = d, khi đó số nút ở mức d = b d .
Tổng số nút được tạo trong trường hợp xấu nhất là b + b 2 + b 3 +… + b d .
Disadvantage- Vì mỗi mức nút được lưu để tạo nút tiếp theo nên nó tiêu tốn rất nhiều dung lượng bộ nhớ. Yêu cầu không gian để lưu trữ các nút là cấp số nhân.
Độ phức tạp của nó phụ thuộc vào số lượng nút. Nó có thể kiểm tra các nút trùng lặp.

Tìm kiếm sâu-đầu tiên
Nó được thực hiện trong đệ quy với cấu trúc dữ liệu ngăn xếp LIFO. Nó tạo cùng một tập hợp các nút như phương thức Breadth-First, chỉ khác thứ tự.
Vì các nút trên đường đơn được lưu trữ trong mỗi lần lặp từ nút gốc đến nút lá, yêu cầu về không gian để lưu trữ các nút là tuyến tính. Với hệ số phân nhánh b và chiều sâu là m , không gian lưu trữ là bm.
Disadvantage- Thuật toán này có thể không kết thúc và tiếp tục vô hạn trên một con đường. Giải pháp cho vấn đề này là chọn độ sâu cắt. Nếu ngưỡng lý tưởng là d và nếu ngưỡng được chọn nhỏ hơn d , thì thuật toán này có thể thất bại. Nếu giới hạn được chọn lớn hơn d , thì thời gian thực hiện sẽ tăng lên.
Độ phức tạp của nó phụ thuộc vào số lượng đường dẫn. Nó không thể kiểm tra các nút trùng lặp.

Tìm kiếm hai chiều
Nó tìm kiếm về phía trước từ trạng thái ban đầu và lùi lại từ trạng thái mục tiêu cho đến khi cả hai gặp nhau để xác định một trạng thái chung.
Đường dẫn từ trạng thái ban đầu được nối với đường dẫn nghịch đảo từ trạng thái mục tiêu. Mỗi lần tìm kiếm chỉ được thực hiện tối đa một nửa tổng số đường dẫn.
Tìm kiếm Chi phí Thống nhất
Việc sắp xếp được thực hiện làm tăng chi phí của đường dẫn đến một nút. Nó luôn luôn mở rộng nút có chi phí thấp nhất. Nó giống với tìm kiếm Breadth First nếu mỗi lần chuyển đổi có cùng chi phí.
Nó khám phá các con đường theo thứ tự tăng dần của chi phí.
Disadvantage- Có thể có nhiều đường đi dài với chi phí ≤ C *. Tìm kiếm Chi phí thống nhất phải khám phá tất cả chúng.
Độ sâu lặp đi lặp lại-Tìm kiếm đầu tiên
Nó thực hiện tìm kiếm theo chiều sâu đến cấp độ 1, bắt đầu lại, thực hiện tìm kiếm theo chiều sâu hoàn chỉnh đến cấp độ 2 và tiếp tục theo cách đó cho đến khi tìm ra giải pháp.
Nó không bao giờ tạo một nút cho đến khi tất cả các nút thấp hơn được tạo. Nó chỉ lưu một đống các nút. Thuật toán kết thúc khi nó tìm thấy lời giải ở độ sâu d . Số nút được tạo ra ở độ sâu d là b d và ở độ sâu d-1 là b d-1.
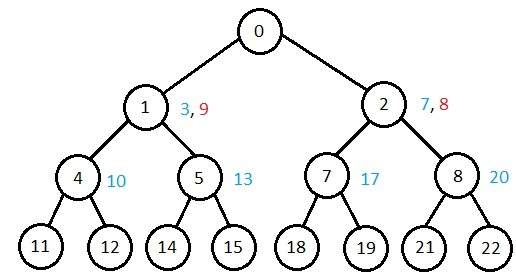
So sánh các thuật toán phức tạp khác nhau
Hãy để chúng tôi xem hiệu suất của các thuật toán dựa trên các tiêu chí khác nhau -
| Tiêu chuẩn | Bề rộng đầu tiên | Độ sâu đầu tiên | Hai chiều | Chi phí thống nhất | Đào sâu tương tác |
|---|---|---|---|---|---|
| Thời gian | b d | b m | b d / 2 | b d | b d |
| Không gian | b d | b m | b d / 2 | b d | b d |
| Sự tối ưu | Đúng | Không | Đúng | Đúng | Đúng |
| Sự hoàn chỉnh | Đúng | Không | Đúng | Đúng | Đúng |
Các chiến lược tìm kiếm được thông báo (Heuristic)
Để giải quyết các vấn đề lớn với số lượng lớn các trạng thái có thể xảy ra, kiến thức cụ thể về vấn đề cần được bổ sung để tăng hiệu quả của thuật toán tìm kiếm.
Các chức năng đánh giá Heuristic
Họ tính toán chi phí của con đường tối ưu giữa hai trạng thái. Một chức năng tính toán cho các trò chơi xếp hình trượt được tính bằng cách đếm số lần di chuyển mà mỗi ô thực hiện từ trạng thái mục tiêu của nó và cộng số lần di chuyển này cho tất cả các ô.
Tìm kiếm Heuristic thuần túy
Nó mở rộng các nút theo thứ tự các giá trị heuristic của chúng. Nó tạo ra hai danh sách, một danh sách đóng cho các nút đã được mở rộng và một danh sách mở cho các nút đã tạo nhưng chưa mở rộng.
Trong mỗi lần lặp, một nút có giá trị heuristic tối thiểu được mở rộng, tất cả các nút con của nó được tạo và đặt trong danh sách đóng. Sau đó, hàm heuristic được áp dụng cho các nút con và chúng được đặt trong danh sách mở theo giá trị heuristic của chúng. Những con đường ngắn hơn được lưu và những con đường dài hơn sẽ bị loại bỏ.
A * Tìm kiếm
Đây là hình thức tìm kiếm Tốt nhất được biết đến nhiều nhất. Nó tránh mở rộng các con đường vốn đã đắt đỏ, nhưng mở rộng hầu hết các con đường hứa hẹn trước.
f (n) = g (n) + h (n), trong đó
- g (n) chi phí (cho đến nay) để đến được nút
- h (n) chi phí ước tính để đi từ nút đến mục tiêu
- f (n) tổng chi phí ước tính của đường dẫn từ n đến mục tiêu. Nó được thực hiện bằng cách sử dụng hàng đợi ưu tiên bằng cách tăng f (n).
Greedy Best First Search
Nó mở rộng nút được ước tính là gần nhất với mục tiêu. Nó mở rộng các nút dựa trên f (n) = h (n). Nó được thực hiện bằng cách sử dụng hàng đợi ưu tiên.
Disadvantage- Nó có thể bị kẹt trong các vòng lặp. Nó không phải là tối ưu.
Thuật toán tìm kiếm cục bộ
Họ bắt đầu từ một giải pháp tương lai và sau đó chuyển sang một giải pháp lân cận. Họ có thể trả về một giải pháp hợp lệ ngay cả khi nó bị gián đoạn bất kỳ lúc nào trước khi chúng kết thúc.
Tìm kiếm leo đồi
Nó là một thuật toán lặp lại bắt đầu với một giải pháp tùy ý cho một vấn đề và cố gắng tìm ra giải pháp tốt hơn bằng cách thay đổi từng bước một phần tử của giải pháp. Nếu sự thay đổi tạo ra một giải pháp tốt hơn, một sự thay đổi gia tăng được coi là một giải pháp mới. Quá trình này được lặp lại cho đến khi không có cải tiến nào nữa.
hàm Hill-Climbing (sự cố), trả về trạng thái là mức tối đa cục bộ.
inputs: problem, a problem
local variables: current, a node
neighbor, a node
current <-Make_Node(Initial-State[problem])
loop
do neighbor <- a highest_valued successor of current
if Value[neighbor] ≤ Value[current] then
return State[current]
current <- neighbor
endDisadvantage - Thuật toán này không hoàn chỉnh, cũng không tối ưu.
Tìm kiếm chùm cục bộ
Trong thuật toán này, nó chứa k số trạng thái tại bất kỳ thời điểm nào. Khi bắt đầu, các trạng thái này được tạo ngẫu nhiên. Kế thừa của k trạng thái này được tính với sự trợ giúp của hàm mục tiêu. Nếu bất kỳ giá trị kế thừa nào là giá trị lớn nhất của hàm mục tiêu, thì thuật toán dừng lại.
Nếu không, (k trạng thái ban đầu và k số trạng thái kế tiếp của các trạng thái = 2k) trạng thái được đặt trong một nhóm. Pool sau đó được sắp xếp theo số. K trạng thái cao nhất được chọn làm trạng thái ban đầu mới. Quá trình này tiếp tục cho đến khi đạt đến giá trị lớn nhất.
hàm BeamSearch ( vấn đề, k ), trả về trạng thái giải pháp.
start with k randomly generated states
loop
generate all successors of all k states
if any of the states = solution, then return the state
else select the k best successors
endỦ mô phỏng
Ủ là quá trình làm nóng và làm lạnh một kim loại để thay đổi cấu trúc bên trong nhằm thay đổi các đặc tính vật lý của nó. Khi kim loại nguội đi, cấu trúc mới của nó được giữ lại và kim loại vẫn giữ được các đặc tính mới thu được. Trong quá trình ủ mô phỏng, nhiệt độ được giữ ở mức thay đổi.
Ban đầu, chúng tôi đặt nhiệt độ cao và sau đó để nhiệt độ 'nguội' từ từ khi thuật toán tiến hành. Khi nhiệt độ cao, thuật toán được phép chấp nhận các giải pháp kém hơn với tần số cao.
Khởi đầu
- Khởi tạo k = 0; L = số nguyên của biến;
- Từ i → j, tìm kiếm hiệu suất Δ.
- If Δ <= 0 then accept else if exp (-Δ / T (k))> random (0,1) then accept;
- Lặp lại các bước 1 và 2 cho các bước L (k).
- k = k + 1;
Lặp lại các bước từ 1 đến 4 cho đến khi các tiêu chí được đáp ứng.
Kết thúc
Vấn đề nhân viên bán hàng đi du lịch
Trong thuật toán này, mục tiêu là tìm một chuyến tham quan chi phí thấp bắt đầu từ một thành phố, thăm tất cả các thành phố trên đường bay chính xác một lần và kết thúc tại cùng một thành phố xuất phát.
Start
Find out all (n -1)! Possible solutions, where n is the total number of cities.
Determine the minimum cost by finding out the cost of each of these (n -1)! solutions.
Finally, keep the one with the minimum cost.
end