Lý thuyết tự động hóa - Hướng dẫn nhanh
Automata - Nó là gì?
Thuật ngữ "Automata" có nguồn gốc từ tiếng Hy Lạp "αὐτόματα" có nghĩa là "tự hoạt động". Automaton (Automata ở dạng số nhiều) là một thiết bị tính toán trừu tượng tự hành, tự động tuân theo một trình tự hoạt động định trước.
Một Automaton với một số trạng thái hữu hạn được gọi là Finite Automaton (FA) hoặc Finite State Machine (FSM).
Định nghĩa chính thức về Automaton hữu hạn
Một Automaton có thể được biểu diễn bằng 5 bộ (Q, ∑, δ, q 0 , F), trong đó -
Q là một tập hợp hữu hạn các trạng thái.
∑ là một tập hợp hữu hạn các ký hiệu, được gọi là alphabet của ô tô.
δ là hàm chuyển tiếp.
q0là trạng thái ban đầu mà từ đó bất kỳ đầu vào nào được xử lý (q 0 ∈ Q).
F là tập hợp các trạng thái / trạng thái cuối cùng của Q (F ⊆ Q).
Các thuật ngữ liên quan
Bảng chữ cái
Definition - An alphabet là bất kỳ bộ ký hiệu hữu hạn nào.
Example - ∑ = {a, b, c, d} là một alphabet set trong đó 'a', 'b', 'c' và 'd' là symbols.
Chuỗi
Definition - A string là một dãy hữu hạn các ký hiệu lấy từ ∑.
Example - 'cabcad' là một chuỗi hợp lệ trên bộ chữ cái ∑ = {a, b, c, d}
Độ dài của một chuỗi
Definition- Là số ký hiệu có trong một chuỗi. (Đóng góp bởi|S|).
Examples -
Nếu S = 'cabcad', | S | = 6
Nếu | S | = 0, nó được gọi là empty string (Đóng góp bởi λ hoặc là ε)
Kleene Star
Definition - Ngôi sao Kleene, ∑*, là một toán tử một ngôi trên một tập hợp các ký hiệu hoặc chuỗi, ∑, điều đó cung cấp cho tập hợp vô hạn tất cả các chuỗi có thể có tất cả các độ dài có thể ∑ kể cả λ.
Representation- ∑ * = ∑ 0 ∪ ∑ 1 ∪ ∑ 2 ∪ ……. trong đó ∑ p là tập hợp tất cả các chuỗi có thể có độ dài p.
Example - Nếu ∑ = {a, b}, ∑ * = {λ, a, b, aa, ab, ba, bb, ……… ..}
Kleene Closure / Plus
Definition - Bộ ∑+ là tập vô hạn của tất cả các chuỗi có thể có tất cả các độ dài có thể trên ∑ không bao gồm λ.
Representation- ∑ + = ∑ 1 ∪ ∑ 2 ∪ ∑ 3 ∪ …….
∑ + = ∑ * - {λ}
Example- Nếu ∑ = {a, b}, ∑ + = {a, b, aa, ab, ba, bb, ……… ..}
Ngôn ngữ
Definition- Một ngôn ngữ là một tập con của ∑ * cho một số bảng chữ cái ∑. Nó có thể là hữu hạn hoặc vô hạn.
Example - Nếu ngôn ngữ nhận tất cả các chuỗi có thể có độ dài 2 trên ∑ = {a, b} thì L = {ab, aa, ba, bb}
Automaton hữu hạn có thể được phân thành hai loại:
- Tự động hóa hữu hạn xác định (DFA)
- Automaton hữu hạn không xác định (NDFA / NFA)
Tự động hóa hữu hạn xác định (DFA)
Trong DFA, đối với mỗi ký hiệu đầu vào, người ta có thể xác định trạng thái mà máy sẽ di chuyển. Do đó, nó được gọi làDeterministic Automaton. Vì nó có một số trạng thái hữu hạn, máy được gọi làDeterministic Finite Machine hoặc là Deterministic Finite Automaton.
Định nghĩa chính thức về DFA
DFA có thể được biểu diễn bằng 5 bộ (Q, ∑, δ, q 0 , F) trong đó -
Q là một tập hợp hữu hạn các trạng thái.
∑ là một tập hợp hữu hạn các ký hiệu được gọi là bảng chữ cái.
δ là hàm chuyển đổi trong đó δ: Q × ∑ → Q
q0là trạng thái ban đầu mà từ đó bất kỳ đầu vào nào được xử lý (q 0 ∈ Q).
F là tập hợp các trạng thái / trạng thái cuối cùng của Q (F ⊆ Q).
Biểu diễn đồ họa của một DFA
DFA được biểu diễn bằng các đồ thị được gọi là state diagram.
- Các đỉnh đại diện cho các trạng thái.
- Các vòng cung được gắn nhãn bằng bảng chữ cái đầu vào hiển thị các chuyển đổi.
- Trạng thái ban đầu được biểu thị bằng một cung tới trống.
- Trạng thái cuối cùng được biểu thị bằng các vòng tròn đôi.
Thí dụ
Cho một tự động hữu hạn xác định là →
- Q = {a, b, c},
- ∑ = {0, 1},
- q 0 = {a},
- F = {c} và
Hàm chuyển đổi δ như bảng sau:
| Trạng thái hiện tại | Trạng thái tiếp theo cho đầu vào 0 | Trạng thái tiếp theo cho đầu vào 1 |
|---|---|---|
| a | a | b |
| b | c | a |
| c | b | c |
Biểu diễn đồ họa của nó sẽ như sau:

Trong NDFA, đối với một ký hiệu đầu vào cụ thể, máy có thể di chuyển đến bất kỳ tổ hợp trạng thái nào trong máy. Nói cách khác, không thể xác định chính xác trạng thái mà máy chuyển động. Do đó, nó được gọi làNon-deterministic Automaton. Vì nó có số trạng thái hữu hạn, máy được gọi làNon-deterministic Finite Machine hoặc là Non-deterministic Finite Automaton.
Định nghĩa chính thức của một NDFA
NDFA có thể được biểu diễn bằng 5 bộ (Q, ∑, δ, q 0 , F) trong đó -
Q là một tập hợp hữu hạn các trạng thái.
∑ là một tập hợp hữu hạn các ký hiệu được gọi là các bảng chữ cái.
δlà hàm chuyển tiếp trong đó δ: Q × ∑ → 2 Q
(Ở đây tập hợp lũy thừa của Q (2 Q ) đã được lấy vì trong trường hợp NDFA, từ một trạng thái, chuyển đổi có thể xảy ra thành bất kỳ sự kết hợp nào của Q trạng thái)
q0là trạng thái ban đầu mà từ đó bất kỳ đầu vào nào được xử lý (q 0 ∈ Q).
F là tập hợp các trạng thái / trạng thái cuối cùng của Q (F ⊆ Q).
Biểu diễn đồ họa của một NDFA: (giống như DFA)
NDFA được biểu diễn bằng các đồ thị được gọi là biểu đồ trạng thái.
- Các đỉnh đại diện cho các trạng thái.
- Các vòng cung được gắn nhãn bằng bảng chữ cái đầu vào hiển thị các chuyển đổi.
- Trạng thái ban đầu được biểu thị bằng một cung tới trống.
- Trạng thái cuối cùng được biểu thị bằng các vòng tròn đôi.
Example
Cho một tự động hữu hạn không xác định được →
- Q = {a, b, c}
- ∑ = {0, 1}
- q 0 = {a}
- F = {c}
Hàm chuyển đổi δ như hình dưới đây -
| Trạng thái hiện tại | Trạng thái tiếp theo cho đầu vào 0 | Trạng thái tiếp theo cho đầu vào 1 |
|---|---|---|
| a | a, b | b |
| b | c | AC |
| c | b, c | c |
Biểu diễn đồ họa của nó sẽ như sau:
DFA so với NDFA
Bảng sau liệt kê sự khác biệt giữa DFA và NDFA.
| DFA | NDFA |
|---|---|
| Sự chuyển đổi từ một trạng thái là một trạng thái tiếp theo cụ thể cho mỗi ký hiệu đầu vào. Do đó nó được gọi là xác định . | Việc chuyển đổi từ một trạng thái có thể là nhiều trạng thái tiếp theo cho mỗi ký hiệu đầu vào. Do đó nó được gọi là không xác định . |
| Chuyển đổi chuỗi trống không được nhìn thấy trong DFA. | NDFA cho phép chuyển đổi chuỗi trống. |
| Bẻ khóa ngược được phép trong DFA | Trong NDFA, không phải lúc nào cũng có thể bẻ khóa ngược. |
| Yêu cầu nhiều không gian hơn. | Yêu cầu ít không gian hơn. |
| Một chuỗi được chấp nhận bởi DFA, nếu nó chuyển sang trạng thái cuối cùng. | Một chuỗi được NDFA chấp nhận, nếu ít nhất một trong tất cả các chuyển đổi có thể kết thúc ở trạng thái cuối cùng. |
Bộ chấp nhận, bộ phân loại và bộ chuyển đổi
Người chấp nhận (Công nhận)
Một Automaton tính toán một hàm Boolean được gọi là acceptor. Tất cả các trạng thái của bộ chấp nhận là chấp nhận hoặc từ chối các đầu vào được cung cấp cho nó.
Phân loại
A classifier có nhiều hơn hai trạng thái cuối cùng và nó cho một đầu ra duy nhất khi nó kết thúc.
Đầu dò
Một Automaton tạo ra đầu ra dựa trên đầu vào hiện tại và / hoặc trạng thái trước đó được gọi là transducer. Đầu dò có thể có hai loại -
Mealy Machine - Đầu ra phụ thuộc cả vào trạng thái hiện tại và đầu vào hiện tại.
Moore Machine - Đầu ra chỉ phụ thuộc vào trạng thái hiện tại.
Khả năng chấp nhận của DFA và NDFA
Một chuỗi được chấp nhận bởi DFA / NDFA và DFA / NDFA bắt đầu ở trạng thái ban đầu sẽ kết thúc ở trạng thái chấp nhận (bất kỳ trạng thái cuối cùng nào) sau khi đọc toàn bộ chuỗi.
Chuỗi S được chấp nhận bởi DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S) ∈ F
Ngôn ngữ L được chấp nhận bởi DFA / NDFA là
{S | S ∈ ∑* and δ*(q0, S) ∈ F}
Chuỗi S ′ không được chấp nhận bởi DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S′) ∉ F
Ngôn ngữ L ′ không được DFA / NDFA chấp nhận (Bổ sung ngôn ngữ L được chấp nhận) là
{S | S ∈ ∑* and δ*(q0, S) ∉ F}
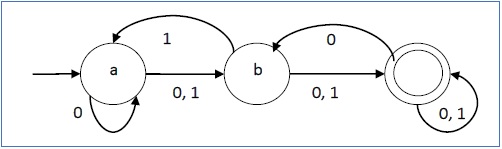
Example
Chúng ta hãy xem xét DFA được thể hiện trong Hình 1.3. Từ DFA, các chuỗi được chấp nhận có thể được rút ra.

Các chuỗi được chấp nhận bởi DFA ở trên: {0, 00, 11, 010, 101, ...........}
Các chuỗi không được DFA ở trên chấp nhận: {1, 011, 111, ........}
Báo cáo vấn đề
Để cho X = (Qx, ∑, δx, q0, Fx)là NDFA chấp nhận ngôn ngữ L (X). Chúng tôi phải thiết kế một DFA tương đươngY = (Qy, ∑, δy, q0, Fy) như vậy mà L(Y) = L(X). Quy trình sau đây chuyển đổi NDFA thành DFA tương đương của nó:
Thuật toán
Input - NDFA
Output - Một DFA tương đương
Step 1 - Tạo bảng trạng thái từ NDFA đã cho.
Step 2 - Tạo một bảng trạng thái trống dưới các bảng chữ cái đầu vào có thể có cho DFA tương đương.
Step 3 - Đánh dấu trạng thái bắt đầu của DFA bằng q0 (Giống như NDFA).
Step 4- Tìm ra sự kết hợp của các Bang {Q 0 , Q 1 , ..., Q n } cho mỗi bảng chữ cái đầu vào có thể có.
Step 5 - Mỗi khi chúng tôi tạo một trạng thái DFA mới dưới các cột bảng chữ cái đầu vào, chúng tôi phải áp dụng lại bước 4, nếu không thì chuyển sang bước 6.
Step 6 - Các trạng thái chứa bất kỳ trạng thái cuối cùng nào của NDFA là trạng thái cuối cùng của DFA tương đương.
Thí dụ
Chúng ta hãy xem xét NDFA được thể hiện trong hình bên dưới.

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| a | {a, b, c, d, e} | {d, e} |
| b | {c} | {e} |
| c | ∅ | {b} |
| d | {e} | ∅ |
| e | ∅ | ∅ |
Sử dụng thuật toán trên, chúng tôi tìm thấy DFA tương đương của nó. Bảng trạng thái của DFA được hiển thị bên dưới.
| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| [a] | [a, b, c, d, e] | [d, e] |
| [a, b, c, d, e] | [a, b, c, d, e] | [b, d, e] |
| [d, e] | [e] | ∅ |
| [b, d, e] | [c, e] | [e] |
| [e] | ∅ | ∅ |
| [c, e] | ∅ | [b] |
| [b] | [c] | [e] |
| [c] | ∅ | [b] |
Biểu đồ trạng thái của DFA như sau:

Giảm thiểu DFA bằng Định lý Myhill-Nerode
Thuật toán
Input - DFA
Output - DFA giảm thiểu
Step 1- Vẽ một bảng cho tất cả các cặp trạng thái (Q i , Q j ) không nhất thiết phải kết nối trực tiếp [Tất cả đều không được đánh dấu ban đầu]
Step 2- Xem xét mọi cặp trạng thái (Q i , Q j ) trong DFA trong đó Q i ∈ F và Q j ∉ F hoặc ngược lại và đánh dấu chúng. [Ở đây F là tập hợp các trạng thái cuối cùng]
Step 3 - Lặp lại bước này cho đến khi chúng ta không thể đánh dấu trạng thái nữa -
Nếu có một cặp chưa được đánh dấu (Q i , Q j ), hãy đánh dấu nó nếu cặp {δ (Q i , A), δ (Q i , A)} được đánh dấu cho một số bảng chữ cái đầu vào.
Step 4- Kết hợp tất cả các cặp không được đánh dấu (Q i , Q j ) và biến chúng thành một trạng thái duy nhất trong DFA giảm.
Thí dụ
Hãy để chúng tôi sử dụng Thuật toán 2 để giảm thiểu DFA được hiển thị bên dưới.

Step 1 - Chúng tôi vẽ một bảng cho tất cả các cặp trạng thái.
| a | b | c | d | e | f | |
| a | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| e | ||||||
| f |
Step 2 - Chúng tôi đánh dấu các cặp trạng thái.
| a | b | c | d | e | f | |
| a | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ |
Step 3- Chúng tôi sẽ cố gắng đánh dấu các cặp trạng thái, với dấu kiểm màu xanh lá cây, chuyển tiếp. Nếu chúng ta nhập 1 vào trạng thái 'a' và 'f', nó sẽ chuyển sang trạng thái 'c' và 'f' tương ứng. (c, f) đã được đánh dấu, do đó chúng ta sẽ đánh dấu cặp (a, f). Bây giờ, chúng ta nhập 1 vào trạng thái 'b' và 'f'; nó sẽ chuyển sang trạng thái 'd' và 'f' tương ứng. (d, f) đã được đánh dấu, do đó chúng ta sẽ đánh dấu cặp (b, f).
| a | b | c | d | e | f | |
| a | ||||||
| b | ||||||
| c | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| e | ✔ | ✔ | ||||
| f | ✔ | ✔ | ✔ | ✔ | ✔ |
Sau bước 3, chúng ta có các tổ hợp trạng thái {a, b} {c, d} {c, e} {d, e} không được đánh dấu.
Chúng ta có thể kết hợp lại {c, d} {c, e} {d, e} thành {c, d, e}
Do đó, chúng tôi có hai trạng thái kết hợp là - {a, b} và {c, d, e}
Vì vậy, DFA thu nhỏ cuối cùng sẽ chứa ba trạng thái {f}, {a, b} và {c, d, e}
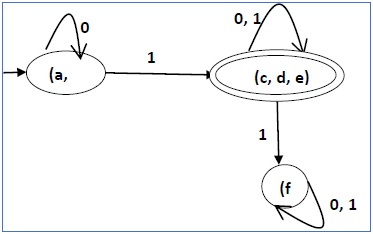
Giảm thiểu DFA sử dụng Định lý Tương đương
Nếu X và Y là hai trạng thái trong DFA, chúng ta có thể kết hợp hai trạng thái này thành {X, Y} nếu chúng không thể phân biệt được. Hai trạng thái có thể phân biệt được, nếu có ít nhất một chuỗi S, sao cho một trong số δ (X, S) và δ (Y, S) đang chấp nhận và một chuỗi khác không chấp nhận. Do đó, DFA là tối thiểu nếu và chỉ khi tất cả các trạng thái đều có thể phân biệt được.
Thuật toán 3
Step 1 - Tất cả các tiểu bang Q được chia thành hai phân vùng - final states và non-final states và được ký hiệu bởi P0. Tất cả các trạng thái trong một phân vùng là tương đương thứ 0 . Tính tiềnk và khởi tạo nó bằng 0.
Step 2- Tăng k bằng 1. Với mỗi phân hoạch trong P k , chia các trạng thái trong P k thành hai phân hoạch nếu chúng phân biệt được k. Hai trạng thái trong phân vùng này X và Y không phân biệt được nếu có một đầu vàoS như vậy mà δ(X, S) và δ(Y, S) là (k-1) -không thể phân biệt được.
Step 3- Nếu P k ≠ P k-1 , lặp lại Bước 2, nếu không thì chuyển sang Bước 4.
Step 4- Kết hợp k thứ bộ tương đương và làm cho họ các bang mới của giảm DFA.
Thí dụ
Chúng ta hãy xem xét DFA sau:

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| a | b | c |
| b | a | d |
| c | e | f |
| d | e | f |
| e | e | f |
| f | f | f |
Hãy để chúng tôi áp dụng thuật toán trên cho DFA ở trên -
- P 0 = {(c, d, e), (a, b, f)}
- P 1 = {(c, d, e), (a, b), (f)}
- P 2 = {(c, d, e), (a, b), (f)}
Do đó, P 1 = P 2 .
Có ba trạng thái trong DFA giảm. DFA giảm như sau:
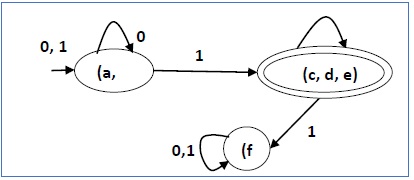
| Q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| (a, b) | (a, b) | (c, d, e) |
| (c, d, e) | (c, d, e) | (f) |
| (f) | (f) | (f) |
Dữ liệu tự động hữu hạn có thể có các đầu ra tương ứng với mỗi lần chuyển đổi. Có hai loại máy trạng thái hữu hạn tạo ra đầu ra -
- Máy Mealy
- Máy Moore
Máy Mealy
Máy Mealy là một FSM có đầu ra phụ thuộc vào trạng thái hiện tại cũng như đầu vào hiện tại.
Nó có thể được mô tả bằng 6 bộ (Q, ∑, O, δ, X, q 0 ) trong đó -
Q là một tập hợp hữu hạn các trạng thái.
∑ là một tập hợp hữu hạn các ký hiệu được gọi là bảng chữ cái đầu vào.
O là một tập hợp hữu hạn các ký hiệu được gọi là bảng chữ cái đầu ra.
δ là hàm chuyển đổi đầu vào trong đó δ: Q × ∑ → Q
X là hàm chuyển đổi đầu ra trong đó X: Q × ∑ → O
q0là trạng thái ban đầu mà từ đó bất kỳ đầu vào nào được xử lý (q 0 ∈ Q).
Bảng trạng thái của Máy Mealy được hiển thị bên dưới:
| Trạng thái hiện tại | Trạng thái tiếp theo | |||
|---|---|---|---|---|
| đầu vào = 0 | đầu vào = 1 | |||
| Tiểu bang | Đầu ra | Tiểu bang | Đầu ra | |
| → a | b | x 1 | c | x 1 |
| b | b | x 2 | d | x 3 |
| c | d | x 3 | c | x 1 |
| d | d | x 3 | d | x 2 |
Biểu đồ trạng thái của Máy Mealy ở trên là -

Máy Moore
Máy Moore là một FSM có đầu ra chỉ phụ thuộc vào trạng thái hiện tại.
Máy Moore có thể được mô tả bằng 6 bộ (Q, ∑, O, δ, X, q 0 ) trong đó -
Q là một tập hợp hữu hạn các trạng thái.
∑ là một tập hợp hữu hạn các ký hiệu được gọi là bảng chữ cái đầu vào.
O là một tập hợp hữu hạn các ký hiệu được gọi là bảng chữ cái đầu ra.
δ là hàm chuyển đổi đầu vào trong đó δ: Q × ∑ → Q
X là hàm chuyển đổi đầu ra trong đó X: Q → O
q0là trạng thái ban đầu mà từ đó bất kỳ đầu vào nào được xử lý (q 0 ∈ Q).
Bảng trạng thái của Máy Moore được hiển thị bên dưới:
| Trạng thái hiện tại | Trạng thái tiếp theo | Đầu ra | |
|---|---|---|---|
| Đầu vào = 0 | Đầu vào = 1 | ||
| → a | b | c | x 2 |
| b | b | d | x 1 |
| c | c | d | x 2 |
| d | d | d | x 3 |
Biểu đồ trạng thái của Máy Moore ở trên là -

Máy Mealy so với Máy Moore
Bảng sau đây nêu rõ những điểm phân biệt Máy Mealy với Máy Moore.
| Máy Mealy | Máy Moore |
|---|---|
| Đầu ra phụ thuộc cả vào trạng thái hiện tại và đầu vào hiện tại | Sản lượng chỉ phụ thuộc vào trạng thái hiện tại. |
| Nói chung, nó có ít trạng thái hơn Máy Moore. | Nói chung, nó có nhiều trạng thái hơn Mealy Machine. |
| Giá trị của hàm đầu ra là một hàm của các quá trình chuyển đổi và thay đổi, khi logic đầu vào ở trạng thái hiện tại được thực hiện. | Giá trị của hàm đầu ra là một hàm của trạng thái hiện tại và các thay đổi ở các cạnh đồng hồ, bất cứ khi nào xảy ra thay đổi trạng thái. |
| Máy Mealy phản ứng nhanh hơn với đầu vào. Chúng thường phản ứng trong cùng một chu kỳ đồng hồ. | Trong máy Moore, cần nhiều logic hơn để giải mã các đầu ra dẫn đến nhiều độ trễ mạch hơn. Chúng thường phản ứng sau một chu kỳ đồng hồ. |
Máy Moore đến Máy Mealy
Thuật toán 4
Input - Máy Moore
Output - Máy Mealy
Step 1 - Lấy định dạng bảng chuyển tiếp Mealy Machine trống.
Step 2 - Sao chép tất cả các trạng thái chuyển tiếp của Máy Moore vào định dạng bảng này.
Step 3- Kiểm tra trạng thái hiện tại và đầu ra tương ứng của chúng trong bảng trạng thái Máy Moore; nếu đối với trạng thái Q i đầu ra là m, hãy sao chép nó vào các cột đầu ra của bảng trạng thái Máy Mealy ở bất cứ nơi nào Q i xuất hiện ở trạng thái tiếp theo.
Thí dụ
Chúng ta hãy xem xét máy Moore sau:
| Trạng thái hiện tại | Trạng thái tiếp theo | Đầu ra | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | d | b | 1 |
| b | a | d | 0 |
| c | c | c | 0 |
| d | b | a | 1 |
Bây giờ chúng tôi áp dụng Thuật toán 4 để chuyển đổi nó thành Máy Mealy.
Step 1 & 2 -
| Trạng thái hiện tại | Trạng thái tiếp theo | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Tiểu bang | Đầu ra | Tiểu bang | Đầu ra | |
| → a | d | b | ||
| b | a | d | ||
| c | c | c | ||
| d | b | a | ||
Step 3 -
| Trạng thái hiện tại | Trạng thái tiếp theo | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Tiểu bang | Đầu ra | Tiểu bang | Đầu ra | |
| => a | d | 1 | b | 0 |
| b | a | 1 | d | 1 |
| c | c | 0 | c | 0 |
| d | b | 0 | a | 1 |
Máy Mealy đến Máy Moore
Thuật toán 5
Input - Máy Mealy
Output - Máy Moore
Step 1- Tính số lượng đầu ra khác nhau cho mỗi trạng thái (Q i ) có sẵn trong bảng trạng thái của máy Mealy.
Step 2- Nếu tất cả các đầu ra của Qi giống nhau, hãy sao chép trạng thái Q i . Nếu nó có n đầu ra riêng biệt, hãy ngắt Q i thành n trạng thái là Q trong đón = 0, 1, 2 .......
Step 3 - Nếu đầu ra của trạng thái ban đầu là 1, hãy chèn một trạng thái ban đầu mới vào đầu cho đầu ra 0.
Thí dụ
Chúng ta hãy xem xét Máy Mealy sau đây -
| Trạng thái hiện tại | Trạng thái tiếp theo | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Trạng thái tiếp theo | Đầu ra | Trạng thái tiếp theo | Đầu ra | |
| → a | d | 0 | b | 1 |
| b | a | 1 | d | 0 |
| c | c | 1 | c | 0 |
| d | b | 0 | a | 1 |
Ở đây, trạng thái 'a' và 'd' chỉ cho kết quả đầu ra tương ứng là 1 và 0, vì vậy chúng tôi giữ lại trạng thái 'a' và 'd'. Nhưng trạng thái 'b' và 'c' tạo ra các đầu ra khác nhau (1 và 0). Vì vậy, chúng tôi chiab thành b0, b1 và c thành c0, c1.
| Trạng thái hiện tại | Trạng thái tiếp theo | Đầu ra | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → a | d | b 1 | 1 |
| b 0 | a | d | 0 |
| b 1 | a | d | 1 |
| c 0 | c 1 | C 0 | 0 |
| c 1 | c 1 | C 0 | 1 |
| d | b 0 | a | 0 |
n theo nghĩa văn học của thuật ngữ, ngữ pháp biểu thị các quy tắc cú pháp cho hội thoại trong ngôn ngữ tự nhiên. Ngôn ngữ học đã cố gắng xác định ngữ pháp kể từ khi ra đời các ngôn ngữ tự nhiên như tiếng Anh, tiếng Phạn, tiếng Quan Thoại, v.v.
Lý thuyết về các ngôn ngữ hình thức có khả năng ứng dụng rộng rãi trong các lĩnh vực Khoa học Máy tính. Noam Chomsky đã đưa ra một mô hình toán học về ngữ pháp vào năm 1956 hiệu quả để viết ngôn ngữ máy tính.
Ngữ pháp
Một ngữ pháp G có thể được viết chính thức dưới dạng 4 bộ (N, T, S, P) trong đó -
N hoặc là VN là một tập hợp các biến hoặc các ký hiệu không đầu cuối.
T hoặc là ∑ là một tập hợp các ký hiệu Terminal.
S là một biến đặc biệt được gọi là ký hiệu Bắt đầu, S ∈ N
Plà Quy tắc sản xuất cho Thiết bị đầu cuối và Không thiết bị đầu cuối. Một nguyên tắc sản xuất có dạng α → β, nơi α và β là chuỗi trên V N ∪ Σ và một biểu tượng nhất của α thuộc về V N .
Thí dụ
Ngữ pháp G1 -
({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})
Đây,
S, A, và B là các ký hiệu không đầu cuối;
a và b là các ký hiệu đầu cuối
S là ký hiệu Bắt đầu, S ∈ N
Sản xuất, P : S → AB, A → a, B → b
Thí dụ
Ngữ pháp G2 -
(({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Đây,
S và A là các ký hiệu không đầu cuối.
a và b là các ký hiệu đầu cuối.
ε là một chuỗi rỗng.
S là ký hiệu Bắt đầu, S ∈ N
Sản xuất P : S → aAb, aA → aaAb, A → ε
Nguồn gốc từ ngữ pháp
Các chuỗi có thể bắt nguồn từ các chuỗi khác bằng cách sử dụng các sản phẩm trong một ngữ pháp. Nếu một ngữ phápG có một sản xuất α → β, chúng ta có thể nói về điều đó x α y dẫn xuất x β y trong G. Dẫn xuất này được viết là -
x α y ⇒G x β y
Thí dụ
Chúng ta hãy xem xét ngữ pháp -
G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Một số chuỗi có thể được dẫn xuất là:
S ⇒ aA b sử dụng sản xuất S → aAb
⇒ a aA bb sử dụng sản xuất aA → aAb
⇒ aaa A bbb sử dụng sản xuất aA → aAb
⇒ aaabbb sử dụng sản xuất A → ε
Tập hợp tất cả các chuỗi có thể bắt nguồn từ một ngữ pháp được cho là ngôn ngữ được tạo ra từ ngữ pháp đó. Một ngôn ngữ được tạo ra bởi một ngữ phápG là một tập hợp con được xác định chính thức bởi
L (G) = {W | W ∈ ∑ *, S ⇒ G W }
Nếu L(G1) = L(G2), ngữ pháp G1 tương đương với Ngữ pháp G2.
Thí dụ
Nếu có một ngữ pháp
G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}
Đây S sản xuất ABvà chúng tôi có thể thay thế A bởi avà B bởi b. Ở đây, chuỗi duy nhất được chấp nhận làab, I E,
L (G) = {ab}
Thí dụ
Giả sử chúng ta có ngữ pháp sau:
G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA | a, B → bB | b}
Ngôn ngữ do ngữ pháp này tạo ra -
L (G) = {ab, a 2 b, ab 2 , a 2 b 2 , ………}
= {a m b n | m ≥ 1 và n ≥ 1}
Xây dựng ngữ pháp Tạo ra một ngôn ngữ
Chúng tôi sẽ xem xét một số ngôn ngữ và chuyển nó thành ngữ pháp G để tạo ra các ngôn ngữ đó.
Thí dụ
Problem- Giả sử, L (G) = {a m b n | m ≥ 0 và n> 0}. Chúng ta phải tìm ra ngữ phápG sản xuất L(G).
Solution
Vì L (G) = {a m b n | m ≥ 0 và n> 0}
tập hợp các chuỗi được chấp nhận có thể được viết lại thành -
L (G) = {b, ab, bb, aab, abb, …….}
Ở đây, biểu tượng bắt đầu phải có ít nhất một chữ 'b' trước bất kỳ số 'a' nào kể cả null.
Để chấp nhận tập hợp chuỗi {b, ab, bb, aab, abb, …….}, Chúng tôi đã thực hiện các sản phẩm -
S → aS, S → B, B → b và B → bB
S → B → b (Được chấp nhận)
S → B → bB → bb (Được chấp nhận)
S → aS → aB → ab (Được chấp nhận)
S → aS → aaS → aaB → aab (Được chấp nhận)
S → aS → aB → abB → abb (Được chấp nhận)
Do đó, chúng ta có thể chứng minh rằng mọi chuỗi đơn trong L (G) đều được chấp nhận bởi ngôn ngữ do tập sản xuất tạo ra.
Do đó ngữ pháp -
G: ({S, A, B}, {a, b}, S, {S → aS | B, B → b | bB})
Thí dụ
Problem- Giả sử, L (G) = {a m b n | m> 0 và n ≥ 0}. Chúng ta phải tìm ra ngữ pháp G tạo ra L (G).
Solution -
Vì L (G) = {a m b n | m> 0 và n ≥ 0}, tập hợp các chuỗi được chấp nhận có thể được viết lại thành -
L (G) = {a, aa, ab, aaa, aab, abb, …….}
Ở đây, biểu tượng bắt đầu phải nhận ít nhất một chữ 'a' theo sau là bất kỳ số chữ 'b' nào kể cả null.
Để chấp nhận tập hợp chuỗi {a, aa, ab, aaa, aab, abb, …….}, Chúng tôi đã thực hiện các sản phẩm -
S → aA, A → aA, A → B, B → bB, B → λ
S → aA → aB → aλ → a (Được chấp nhận)
S → aA → aaA → aaB → aaλ → aa (Được chấp nhận)
S → aA → aB → abB → abλ → ab (Chấp nhận)
S → aA → aaA → aaaA → aaaB → aaaλ → aaa (Được chấp nhận)
S → aA → aaA → aaB → aabB → aabλ → aab (Được chấp nhận)
S → aA → aB → abB → abbB → abbλ → abb (Chấp nhận)
Do đó, chúng ta có thể chứng minh rằng mọi chuỗi đơn trong L (G) đều được chấp nhận bởi ngôn ngữ do tập sản xuất tạo ra.
Do đó ngữ pháp -
G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB})
Theo Noam Chomosky, có bốn loại ngữ pháp - Loại 0, Loại 1, Loại 2 và Loại 3. Bảng sau đây cho thấy chúng khác nhau như thế nào -
| Loại ngữ pháp | Ngữ pháp được chấp nhận | Ngôn ngữ được chấp nhận | Automaton |
|---|---|---|---|
| Loại 0 | Ngữ pháp không hạn chế | Ngôn ngữ liệt kê đệ quy | Máy turing |
| Loại 1 | Ngữ pháp nhạy cảm theo ngữ cảnh | Ngôn ngữ nhạy cảm với ngữ cảnh | Automaton giới hạn tuyến tính |
| Loại 2 | Ngữ pháp không theo ngữ cảnh | Ngôn ngữ không có ngữ cảnh | Tự động đẩy xuống |
| Loại 3 | Ngữ pháp thông thường | Ngôn ngữ thông thường | Automaton trạng thái hữu hạn |
Hãy xem hình minh họa sau đây. Nó cho thấy phạm vi của từng loại ngữ pháp -

Type - 3 Grammar
Type-3 grammars generate regular languages. Type-3 grammars must have a single non-terminal on the left-hand side and a right-hand side consisting of a single terminal or single terminal followed by a single non-terminal.
The productions must be in the form X → a or X → aY
where X, Y ∈ N (Non terminal)
and a ∈ T (Terminal)
The rule S → ε is allowed if S does not appear on the right side of any rule.
Example
X → ε
X → a | aY
Y → bType - 2 Grammar
Type-2 grammars generate context-free languages.
The productions must be in the form A → γ
where A ∈ N (Non terminal)
and γ ∈ (T ∪ N)* (String of terminals and non-terminals).
These languages generated by these grammars are be recognized by a non-deterministic pushdown automaton.
Example
S → X a
X → a
X → aX
X → abc
X → εType - 1 Grammar
Type-1 grammars generate context-sensitive languages. The productions must be in the form
α A β → α γ β
where A ∈ N (Non-terminal)
and α, β, γ ∈ (T ∪ N)* (Strings of terminals and non-terminals)
The strings α and β may be empty, but γ must be non-empty.
The rule S → ε is allowed if S does not appear on the right side of any rule. The languages generated by these grammars are recognized by a linear bounded automaton.
Example
AB → AbBc
A → bcA
B → bType - 0 Grammar
Type-0 grammars generate recursively enumerable languages. The productions have no restrictions. They are any phase structure grammar including all formal grammars.
They generate the languages that are recognized by a Turing machine.
The productions can be in the form of α → β where α is a string of terminals and nonterminals with at least one non-terminal and α cannot be null. β is a string of terminals and non-terminals.
Example
S → ACaB
Bc → acB
CB → DB
aD → DbA Regular Expression can be recursively defined as follows −
ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
φ is a Regular Expression denoting an empty language. (L (φ) = { })
x is a Regular Expression where L = {x}
If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then
X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).
X . Y is a Regular Expression corresponding to the language L(X) . L(Y) where L(X.Y) = L(X) . L(Y)
R* is a Regular Expression corresponding to the language L(R*)where L(R*) = (L(R))*
If we apply any of the rules several times from 1 to 5, they are Regular Expressions.
Some RE Examples
| Regular Expressions | Regular Set |
|---|---|
| (0 + 10*) | L = { 0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | L = {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | L = {ε, 0, 1, 01} |
| (a+b)* | Set of strings of a’s and b’s of any length including the null string. So L = { ε, a, b, aa , ab , bb , ba, aaa…….} |
| (a+b)*abb | Set of strings of a’s and b’s ending with the string abb. So L = {abb, aabb, babb, aaabb, ababb, …………..} |
| (11)* | Set consisting of even number of 1’s including empty string, So L= {ε, 11, 1111, 111111, ……….} |
| (aa)*(bb)*b | Set of strings consisting of even number of a’s followed by odd number of b’s , so L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..} |
| (aa + ab + ba + bb)* | String of a’s and b’s of even length can be obtained by concatenating any combination of the strings aa, ab, ba and bb including null, so L = {aa, ab, ba, bb, aaab, aaba, …………..} |
Any set that represents the value of the Regular Expression is called a Regular Set.
Properties of Regular Sets
Property 1. The union of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(aa)* and RE2 = (aa)*
So, L1 = {a, aaa, aaaaa,.....} (Strings of odd length excluding Null)
and L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}
(Strings of all possible lengths including Null)
RE (L1 ∪ L2) = a* (which is a regular expression itself)
Hence, proved.
Property 2. The intersection of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(a*) and RE2 = (aa)*
So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)
RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.
Hence, proved.
Property 3. The complement of a regular set is regular.
Proof −
Let us take a regular expression −
RE = (aa)*
So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)
Complement of L is all the strings that is not in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
RE (L’) = a(aa)* which is a regular expression itself.
Hence, proved.
Property 4. The difference of two regular set is regular.
Proof −
Let us take two regular expressions −
RE1 = a (a*) and RE2 = (aa)*
So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(Strings of all odd lengths excluding Null)
RE (L1 – L2) = a (aa)* which is a regular expression.
Hence, proved.
Property 5. The reversal of a regular set is regular.
Proof −
We have to prove LR is also regular if L is a regular set.
Let, L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10 which is regular
Hence, proved.
Property 6. The closure of a regular set is regular.
Proof −
If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)
i.e., RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)
RE (L*) = a (a)*
Hence, proved.
Property 7. The concatenation of two regular sets is regular.
Proof −
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
and L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
Identities Related to Regular Expressions
Given R, P, L, Q as regular expressions, the following identities hold −
- ∅* = ε
- ε* = ε
- RR* = R*R
- R*R* = R*
- (R*)* = R*
- RR* = R*R
- (PQ)*P =P(QP)*
- (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
- R + ∅ = ∅ + R = R (The identity for union)
- R ε = ε R = R (The identity for concatenation)
- ∅ L = L ∅ = ∅ (The annihilator for concatenation)
- R + R = R (Idempotent law)
- L (M + N) = LM + LN (Left distributive law)
- (M + N) L = ML + NL (Right distributive law)
- ε + RR* = ε + R*R = R*
In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.
Statement −
Let P and Q be two regular expressions.
If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*
Proof −
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the following equation −
R = Q + QP + QP2 + QP3…..
R = Q (ε + P + P2 + P3 + …. )
R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]
Hence, proved.
Assumptions for Applying Arden’s Theorem
- The transition diagram must not have NULL transitions
- It must have only one initial state
Method
Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q1.
q1 = q1R11 + q2R21 + … + qnRn1 + ε
q2 = q1R12 + q2R22 + … + qnRn2
…………………………
…………………………
…………………………
…………………………
qn = q1R1n + q2R2n + … + qnRnn
Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅
Step 2 − Solve these equations to get the equation for the final state in terms of Rij
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state and final state is q1.
The equations for the three states q1, q2, and q3 are as follows −
q1 = q1a + q3a + ε (ε move is because q1 is the initial state0
q2 = q1b + q2b + q3b
q3 = q2a
Now, we will solve these three equations −
q2 = q1b + q2b + q3b
= q1b + q2b + (q2a)b (Substituting value of q3)
= q1b + q2(b + ab)
= q1b (b + ab)* (Applying Arden’s Theorem)
q1 = q1a + q3a + ε
= q1a + q2aa + ε (Substituting value of q3)
= q1a + q1b(b + ab*)aa + ε (Substituting value of q2)
= q1(a + b(b + ab)*aa) + ε
= ε (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*.
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state is q1 and the final state is q2
Now we write down the equations −
q1 = q10 + ε
q2 = q11 + q20
q3 = q21 + q30 + q31
Now, we will solve these three equations −
q1 = ε0* [As, εR = R]
So, q1 = 0*
q2 = 0*1 + q20
So, q2 = 0*1(0)* [By Arden’s theorem]
Hence, the regular expression is 0*10*.
We can use Thompson's Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.
Some basic RA expressions are the following −
Case 1 − For a regular expression ‘a’, we can construct the following FA −

Case 2 − For a regular expression ‘ab’, we can construct the following FA −

Case 3 − For a regular expression (a+b), we can construct the following FA −

Case 4 − For a regular expression (a+b)*, we can construct the following FA −

Method
Step 1 Construct an NFA with Null moves from the given regular expression.
Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.
Problem
Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0
Solution
We will concatenate three expressions "1", "(0 + 1)*" and "0"

Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.
Finite Automata with Null Moves (NFA-ε)
A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.
An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of
Q − a finite set of states
∑ − a finite set of input symbols
δ − a transition function δ : Q × (∑ ∪ {ε}) → 2Q
q0 − an initial state q0 ∈ Q
F − a set of final state/states of Q (F⊆Q).

The above (FA-ε) accepts a string set − {0, 1, 01}
Removal of Null Moves from Finite Automata
If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −
- Find all the outgoing edges from Y.
- Copy all these edges starting from X without changing the edge labels.
- If X is an initial state, make Y also an initial state.
- If Y is a final state, make X also a final state.
Problem
Convert the following NFA-ε to NFA without Null move.

Solution
Step 1 −
Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.
Here the outgoing edges from qf is to qf for inputs 0 and 1.
Step 2 −
Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −

Step 3 −
Here q1 is an initial state, so we make qf also an initial state.
So the FA becomes −

Step 4 −
Here qf is a final state, so we make q1 also a final state.
So the FA becomes −

Theorem
Let L be a regular language. Then there exists a constant ‘c’ such that for every string w in L −
|w| ≥ c
We can break w into three strings, w = xyz, such that −
- |y| > 0
- |xy| ≤ c
- For all k ≥ 0, the string xykz is also in L.
Applications of Pumping Lemma
Pumping Lemma is to be applied to show that certain languages are not regular. It should never be used to show a language is regular.
If L is regular, it satisfies Pumping Lemma.
If L does not satisfy Pumping Lemma, it is non-regular.
Method to prove that a language L is not regular
At first, we have to assume that L is regular.
So, the pumping lemma should hold for L.
Use the pumping lemma to obtain a contradiction −
Select w such that |w| ≥ c
Select y such that |y| ≥ 1
Select x such that |xy| ≤ c
Assign the remaining string to z.
Select k such that the resulting string is not in L.
Hence L is not regular.
Problem
Prove that L = {aibi | i ≥ 0} is not regular.
Solution −
At first, we assume that L is regular and n is the number of states.
Let w = anbn. Thus |w| = 2n ≥ n.
By pumping lemma, let w = xyz, where |xy| ≤ n.
Let x = ap, y = aq, and z = arbn, where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
Let k = 2. Then xy2z = apa2qarbn.
Number of as = (p + 2q + r) = (p + q + r) + q = n + q
Hence, xy2z = an+q bn. Since q ≠ 0, xy2z is not of the form anbn.
Thus, xy2z is not in L. Hence L is not regular.
If (Q, ∑, δ, q0, F) be a DFA that accepts a language L, then the complement of the DFA can be obtained by swapping its accepting states with its non-accepting states and vice versa.
We will take an example and elaborate this below −

This DFA accepts the language
L = {a, aa, aaa , ............. }
over the alphabet
∑ = {a, b}
So, RE = a+.
Now we will swap its accepting states with its non-accepting states and vice versa and will get the following −

This DFA accepts the language
Ľ = {ε, b, ab ,bb,ba, ............... }
over the alphabet
∑ = {a, b}
Note − If we want to complement an NFA, we have to first convert it to DFA and then have to swap states as in the previous method.
Definition − A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where
N is a set of non-terminal symbols.
T is a set of terminals where N ∩ T = NULL.
P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.
S is the start symbol.
Example
- The grammar ({A}, {a, b, c}, P, A), P : A → aA, A → abc.
- The grammar ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- The grammar ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Generation of Derivation Tree
A derivation tree or parse tree is an ordered rooted tree that graphically represents the semantic information a string derived from a context-free grammar.
Representation Technique
Root vertex − Must be labeled by the start symbol.
Vertex − Labeled by a non-terminal symbol.
Leaves − Labeled by a terminal symbol or ε.
If S → x1x2 …… xn is a production rule in a CFG, then the parse tree / derivation tree will be as follows −

There are two different approaches to draw a derivation tree −
Top-down Approach −
Starts with the starting symbol S
Goes down to tree leaves using productions
Bottom-up Approach −
Starts from tree leaves
Proceeds upward to the root which is the starting symbol S
Derivation or Yield of a Tree
The derivation or the yield of a parse tree is the final string obtained by concatenating the labels of the leaves of the tree from left to right, ignoring the Nulls. However, if all the leaves are Null, derivation is Null.
Example
Let a CFG {N,T,P,S} be
N = {S}, T = {a, b}, Starting symbol = S, P = S → SS | aSb | ε
One derivation from the above CFG is “abaabb”
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Sentential Form and Partial Derivation Tree
A partial derivation tree is a sub-tree of a derivation tree/parse tree such that either all of its children are in the sub-tree or none of them are in the sub-tree.
Example
If in any CFG the productions are −
S → AB, A → aaA | ε, B → Bb| ε
the partial derivation tree can be the following −
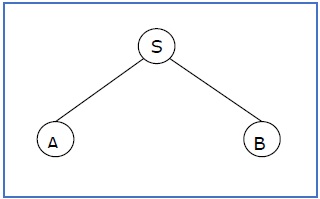
If a partial derivation tree contains the root S, it is called a sentential form. The above sub-tree is also in sentential form.
Leftmost and Rightmost Derivation of a String
Leftmost derivation − A leftmost derivation is obtained by applying production to the leftmost variable in each step.
Rightmost derivation − A rightmost derivation is obtained by applying production to the rightmost variable in each step.
Example
Let any set of production rules in a CFG be
X → X+X | X*X |X| a
over an alphabet {a}.
The leftmost derivation for the string "a+a*a" may be −
X → X+X → a+X → a + X*X → a+a*X → a+a*a
Dẫn xuất từng bước của chuỗi trên được hiển thị như sau:

Dẫn xuất ngoài cùng bên phải cho chuỗi trên "a+a*a" có thể là -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
Dẫn xuất từng bước của chuỗi trên được hiển thị như sau:

Ngữ pháp đệ quy trái và phải
Trong ngữ pháp không có ngữ cảnh G, nếu có sản xuất ở dạng X → Xa Ở đâu X không phải là thiết bị đầu cuối và ‘a’ là một chuỗi các thiết bị đầu cuối, nó được gọi là left recursive production. Ngữ pháp có sản xuất đệ quy bên trái được gọi làleft recursive grammar.
Và nếu trong ngữ pháp không có ngữ cảnh G, nếu có sản xuất thì ở dạng X → aX Ở đâu X không phải là thiết bị đầu cuối và ‘a’ là một chuỗi các thiết bị đầu cuối, nó được gọi là right recursive production. Ngữ pháp có sản xuất đệ quy đúng được gọi làright recursive grammar.
Nếu ngữ pháp không có ngữ cảnh G có nhiều hơn một cây dẫn xuất cho một số chuỗi w ∈ L(G), nó được gọi là ambiguous grammar. Tồn tại nhiều dẫn xuất ngoài cùng bên phải hoặc ngoài cùng bên trái cho một số chuỗi được tạo từ ngữ pháp đó.
Vấn đề
Kiểm tra xem ngữ pháp G với các quy tắc sản xuất -
X → X + X | X * X | X | a
là mơ hồ hay không.
Giải pháp
Hãy cùng tìm hiểu cây dẫn xuất cho chuỗi "a + a * a". Nó có hai nguồn gốc ngoài cùng bên trái.
Derivation 1- X → X + X → a + X → a + X * X → a + a * X → a + a * a
Parse tree 1 -

Derivation 2- X → X * X → X + X * X → a + X * X → a + a * X → a + a * a
Parse tree 2 -

Vì có hai cây phân tích cú pháp cho một chuỗi "a + a * a", ngữ pháp G là mơ hồ.
Ngôn ngữ không có ngữ cảnh là closed dưới -
- Union
- Concatenation
- Hoạt động của Kleene Star
liên hiệp
Cho L 1 và L 2 là hai ngôn ngữ không có ngữ cảnh. Khi đó L 1 ∪ L 2 cũng không có ngữ cảnh.
Thí dụ
Cho L 1 = {a n b n , n> 0}. Văn phạm tương ứng G 1 sẽ có P: S1 → aAb | ab
Cho L 2 = {c m d m , m ≥ 0}. Văn phạm G 2 tương ứng sẽ có P: S2 → cBb | ε
Liên hiệp của L 1 và L 2 , L = L 1 ∪ L 2 = {a n b n } ∪ {c m d m }
Văn phạm tương ứng G sẽ có thêm sản phẩm S → S1 | S2
Kết nối
Nếu L 1 và L 2 là ngôn ngữ không có ngữ cảnh thì L 1 L 2 cũng không có ngữ cảnh.
Thí dụ
Liên hợp các ngôn ngữ L 1 và L 2 , L = L 1 L 2 = {a n b n c m d m }
Văn phạm tương ứng G sẽ có sản lượng bổ sung S → S1 S2
Kleene Star
Nếu L là ngôn ngữ không có ngữ cảnh thì L * cũng không có ngữ cảnh.
Thí dụ
Cho L = {a n b n , n ≥ 0}. Văn phạm G tương ứng sẽ có P: S → aAb | ε
Kleene Star L 1 = {a n b n } *
Ngữ pháp tương ứng G 1 sẽ có thêm các xuất S1 → SS 1 | ε
Ngôn ngữ không có ngữ cảnh là not closed dưới -
Intersection - Nếu L1 và L2 là ngôn ngữ không có ngữ cảnh, thì L1 ∩ L2 không nhất thiết là ngôn ngữ không có ngữ cảnh.
Intersection with Regular Language - Nếu L1 là ngôn ngữ thông thường và L2 là ngôn ngữ không có ngữ cảnh thì L1 ∩ L2 là ngôn ngữ không có ngữ cảnh.
Complement - Nếu L1 là ngôn ngữ không có ngữ cảnh thì L1 'có thể không có ngữ cảnh.
Trong CFG, có thể xảy ra rằng tất cả các quy tắc sản xuất và ký hiệu không cần thiết cho việc lấy ra các chuỗi. Bên cạnh đó, có thể có một số sản phẩm rỗng và sản xuất đơn vị. Loại bỏ các sản phẩm và biểu tượng này được gọi làsimplification of CFGs. Đơn giản hóa về cơ bản bao gồm các bước sau:
- Giảm CFG
- Loại bỏ sản xuất đơn vị
- Loại bỏ các sản phẩm vô hiệu
Giảm CFG
CFG được giảm theo hai giai đoạn -
Phase 1 - Bắt nguồn từ một ngữ pháp tương đương, G’, từ CFG, G, sao cho mỗi biến dẫn xuất một số chuỗi đầu cuối.
Derivation Procedure -
Bước 1 - Bao gồm tất cả các ký hiệu, W1, dẫn xuất một số thiết bị đầu cuối và khởi tạo i=1.
Bước 2 - Bao gồm tất cả các ký hiệu, Wi+1, dẫn xuất Wi.
Bước 3 - Tăng dần i và lặp lại Bước 2, cho đến khi Wi+1 = Wi.
Bước 4 - Bao gồm tất cả các quy tắc sản xuất có Wi trong đó.
Phase 2 - Bắt nguồn từ một ngữ pháp tương đương, G”, từ CFG, G’, sao cho mỗi biểu tượng xuất hiện trong một biểu mẫu ủy nhiệm.
Derivation Procedure -
Bước 1 - Đưa biểu tượng bắt đầu vào Y1 và khởi tạo i = 1.
Bước 2 - Bao gồm tất cả các ký hiệu, Yi+1, có thể bắt nguồn từ Yi và bao gồm tất cả các quy tắc sản xuất đã được áp dụng.
Bước 3 - Tăng dần i và lặp lại Bước 2, cho đến khi Yi+1 = Yi.
Vấn đề
Tìm một văn phạm rút gọn tương đương với văn phạm G, có quy tắc sản xuất, P: S → AC | B, A → a, C → c | BC, E → aA | e
Giải pháp
Phase 1 -
T = {a, c, e}
W 1 = {A, C, E} từ các quy tắc A → a, C → c và E → aA
W 2 = {A, C, E} U {S} từ quy tắc S → AC
W 3 = {A, C, E, S} Ư ∅
Vì W 2 = W 3 , chúng ta có thể suy ra G 'là -
G '= {{A, C, E, S}, {a, c, e}, P, {S}}
trong đó P: S → AC, A → a, C → c, E → aA | e
Phase 2 -
Y 1 = {S}
Y 2 = {S, A, C} từ quy tắc S → AC
Y 3 = {S, A, C, a, c} từ các quy tắc A → a và C → c
Y 4 = {S, A, C, a, c}
Vì Y 3 = Y 4 , chúng ta có thể suy ra G ”là -
G ”= {{A, C, S}, {a, c}, P, {S}}
trong đó P: S → AC, A → a, C → c
Loại bỏ sản xuất đơn vị
Bất kỳ quy tắc sản xuất nào ở dạng A → B trong đó A, B ∈ Không đầu cuối được gọi là unit production..
Thủ tục loại bỏ -
Step 1 - Để loại bỏ A → B, thêm sản xuất A → x quy tắc ngữ pháp bất cứ khi nào B → xxảy ra trong ngữ pháp. [x ∈ Terminal, x có thể là Null]
Step 2 - Xóa A → B từ ngữ pháp.
Step 3 - Lặp lại từ bước 1 cho đến khi loại bỏ tất cả các sản phẩm đơn vị.
Problem
Xóa đơn vị sản xuất khỏi phần sau -
S → XY, X → a, Y → Z | b, Z → M, M → N, N → a
Solution -
Có 3 đơn vị sản xuất trong ngữ pháp -
Y → Z, Z → M và M → N
At first, we will remove M → N.
Khi N → a, chúng ta thêm M → a, và M → N bị loại bỏ.
Bộ sản xuất trở thành
S → XY, X → a, Y → Z | b, Z → M, M → a, N → a
Now we will remove Z → M.
Khi M → a, chúng ta thêm Z → a, và Z → M bị loại bỏ.
Bộ sản xuất trở thành
S → XY, X → a, Y → Z | b, Z → a, M → a, N → a
Now we will remove Y → Z.
Khi Z → a, chúng ta thêm Y → a, và Y → Z bị loại bỏ.
Bộ sản xuất trở thành
S → XY, X → a, Y → a | b, Z → a, M → a, N → a
Bây giờ Z, M và N không thể truy cập được, do đó chúng tôi có thể xóa chúng.
CFG cuối cùng là đơn vị sản xuất miễn phí -
S → XY, X → a, Y → a | b
Loại bỏ các sản phẩm vô hiệu
Trong CFG, một ký hiệu không phải đầu cuối ‘A’ là biến nullable nếu có sản xuất A → ε hoặc có một dẫn xuất bắt đầu từ A và cuối cùng kết thúc với
ε: A → .......… → ε
Thủ tục loại bỏ
Step 1 - Tìm ra các biến không đầu cuối có thể nullable mà suy ra ε.
Step 2 - Đối với mỗi lần sản xuất A → a, xây dựng tất cả các sản phẩm A → x Ở đâu x được lấy từ ‘a’ bằng cách xóa một hoặc nhiều thiết bị không phải thiết bị đầu cuối khỏi Bước 1.
Step 3 - Kết hợp các sản phẩm gốc với kết quả của bước 2 và loại bỏ ε - productions.
Problem
Xóa sản xuất rỗng khỏi phần sau -
S → ASA | aB | b, A → B, B → b | ∈
Solution -
Có hai biến nullable - A và B
At first, we will remove B → ε.
Sau khi loại bỏ B → ε, bộ sản xuất trở thành -
S → ASA | aB | b | a, A ε B | b | & epsilon, B → b
Now we will remove A → ε.
Sau khi loại bỏ A → ε, bộ sản xuất trở thành -
S → ASA | aB | b | a | SA | NHƯ | S, A → B | b, B → b
Đây là tập sản xuất cuối cùng không có quá trình chuyển đổi rỗng.
CFG ở dạng Chomsky Normal nếu Sản phẩm ở các dạng sau:
- A → a
- A → BC
- S → ε
trong đó A, B và C không phải là thiết bị đầu cuối và a là thiết bị đầu cuối.
Thuật toán chuyển thành dạng chuẩn Chomsky -
Step 1 - Nếu ký hiệu bắt đầu S xảy ra ở một số bên phải, tạo một biểu tượng bắt đầu mới S’ và một sản xuất mới S’→ S.
Step 2- Loại bỏ các sản phẩm Null. (Sử dụng thuật toán loại bỏ sản xuất Null đã thảo luận trước đó)
Step 3- Loại bỏ các sản phẩm đơn vị. (Sử dụng thuật toán loại bỏ sản xuất đơn vị đã thảo luận trước đó)
Step 4 - Thay thế từng sản xuất A → B1…Bn Ở đâu n > 2 với A → B1C Ở đâu C → B2 …Bn. Lặp lại bước này cho tất cả các sản phẩm có hai hoặc nhiều ký hiệu ở phía bên phải.
Step 5 - Nếu mặt phải của bất kỳ sản xuất nào ở dạng A → aB nơi a là thiết bị đầu cuối và A, B không phải là thiết bị đầu cuối, sau đó sản xuất được thay thế bằng A → XB và X → a. Lặp lại bước này cho mọi sản xuất ở dạngA → aB.
Vấn đề
Chuyển đổi CFG sau thành CNF
S → ASA | aB, A → B | S, B → b | ε
Giải pháp
(1) Từ S xuất hiện trong RHS, chúng tôi thêm một trạng thái mới S0 và S0→S được thêm vào bộ sản xuất và nó trở thành -
S 0 → S, S → ASA | aB, A → B | S, B → b | ∈
(2) Bây giờ chúng ta sẽ loại bỏ các sản phẩm rỗng -
B → ∈ và A → ∈
Sau khi loại bỏ B → ε, tập hợp sản xuất trở thành -
S 0 → S, S → ASA | aB | a, A → B | S | ∈, B → b
Sau khi loại bỏ A → ∈, tập sản xuất trở thành -
S 0 → S, S → ASA | aB | a | NHƯ | SA | S, A → B | S, B → b
(3) Bây giờ chúng tôi sẽ loại bỏ các sản phẩm đơn vị.
Sau khi loại bỏ S → S, bộ sản xuất trở thành -
S 0 → S, S → ASA | aB | a | NHƯ | SA, A → B | S, B → b
Sau khi loại bỏ S 0 → S, bộ sản xuất trở thành -
S 0 → ASA | aB | a | NHƯ | SA, S → ASA | aB | a | NHƯ | SA
A → B | S, B → b
Sau khi loại bỏ A → B, tập hợp sản xuất trở thành -
S 0 → ASA | aB | a | NHƯ | SA, S → ASA | aB | a | NHƯ | SA
A → S | b
B → b
Sau khi loại bỏ A → S, tập hợp sản xuất trở thành -
S 0 → ASA | aB | a | NHƯ | SA, S → ASA | aB | a | NHƯ | SA
A → b | ASA | aB | a | NHƯ | SA, B → b
(4) Bây giờ chúng ta sẽ tìm ra nhiều hơn hai biến trong RHS
Ở đây, S 0 → ASA, S → ASA, A → ASA vi phạm hai Non-terminal trong RHS
Do đó, chúng tôi sẽ áp dụng bước 4 và bước 5 để có được bộ sản xuất cuối cùng sau đây trong CNF -
S 0 → AX | aB | a | NHƯ | SA
S → AX | aB | a | NHƯ | SA
A → b | AX | aB | a | NHƯ | SA
B → b
X → SA
(5)Chúng ta phải thay đổi các sản phẩm S 0 → aB, S → aB, A → aB
Và tập hợp sản xuất cuối cùng trở thành -
S 0 → AX | YB | a | NHƯ | SA
S → AX | YB | a | NHƯ | SA
A → b A → b | AX | YB | a | NHƯ | SA
B → b
X → SA
Y → a
CFG ở dạng Greibach Normal nếu Sản phẩm ở các dạng sau:
A → b
A → bD 1 … D n
S → ε
trong đó A, D 1 , ...., D n là không đầu cuối và b là đầu cuối.
Thuật toán chuyển đổi CFG thành Dạng chuẩn Greibach
Step 1 - Nếu ký hiệu bắt đầu S xảy ra ở một số bên phải, tạo một biểu tượng bắt đầu mới S’ và một sản xuất mới S’ → S.
Step 2- Loại bỏ các sản phẩm Null. (Sử dụng thuật toán loại bỏ sản xuất Null đã thảo luận trước đó)
Step 3- Loại bỏ các sản phẩm đơn vị. (Sử dụng thuật toán loại bỏ sản xuất đơn vị đã thảo luận trước đó)
Step 4 - Loại bỏ tất cả các đệ quy trái trực tiếp và gián tiếp.
Step 5 - Thực hiện thay thế thích hợp các sản phẩm để chuyển nó thành dạng GNF thích hợp.
Vấn đề
Chuyển đổi CFG sau thành CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o
Giải pháp
Đây, Skhông xuất hiện ở phía bên phải của bất kỳ sản phẩm nào và không có đơn vị hoặc sản phẩm rỗng trong bộ quy tắc sản xuất. Vì vậy, chúng ta có thể bỏ qua Bước 1 đến Bước 3.
Step 4
Bây giờ sau khi thay thế
X trong S → XY | Xo so | p
với
mX | m
chúng tôi đạt được
S → mXY | mY | mXo | mo | p.
Và sau khi thay thế
X trong Y → X n | o
với phía bên phải của
X → mX | m
chúng tôi đạt được
Y → mXn | mn | o.
Hai sản phẩm mới O → o và P → p được thêm vào tập hợp sản xuất và sau đó chúng tôi đi đến GNF cuối cùng như sau:
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p
Bổ đề
Nếu L là một ngôn ngữ không có ngữ cảnh, có độ dài p sao cho bất kỳ chuỗi nào w ∈ L chiều dài ≥ p có thể được viết như w = uvxyz, Ở đâu vy ≠ ε, |vxy| ≤ pvà cho tất cả i ≥ 0, uvixyiz ∈ L.
Các ứng dụng của bổ đề bơm
Bổ đề Pumping được sử dụng để kiểm tra xem một ngữ pháp có phải là ngữ cảnh hay không. Hãy để chúng tôi lấy một ví dụ và chỉ ra cách nó được kiểm tra.
Vấn đề
Tìm hiểu liệu ngôn ngữ L = {xnynzn | n ≥ 1} có ngữ cảnh miễn phí hay không.
Giải pháp
Để cho Lkhông có ngữ cảnh. Sau đó,L phải thỏa mãn bổ đề bơm.
Lúc đầu, hãy chọn một số ncủa bổ đề bơm. Sau đó, lấy z là 0 n 1 n 2 n .
Phá vỡ z thành uvwxy, Ở đâu
|vwx| ≤ n and vx ≠ ε.
Vì thế vwxkhông thể liên quan đến cả 0 và 2, vì 0 cuối cùng và 2 đầu tiên cách nhau ít nhất (n + 1) vị trí. Có hai trường hợp -
Case 1 - vwxkhông có 2s. Sau đóvxchỉ có 0 và 1. Sau đóuwy, mà sẽ phải ở L, có n 2 giây, nhưng ít hơn n 0 hoặc 1s.
Case 2 - vwx không có số 0.
Tại đây xảy ra mâu thuẫn.
Vì thế, L không phải là một ngôn ngữ không có ngữ cảnh.
Cấu trúc cơ bản của PDA
Công cụ tự động đẩy xuống là một cách triển khai ngữ pháp không có ngữ cảnh theo cách tương tự như cách chúng tôi thiết kế DFA cho ngữ pháp thông thường. Một DFA có thể nhớ một lượng thông tin hữu hạn, nhưng một PDA có thể nhớ một lượng thông tin vô hạn.
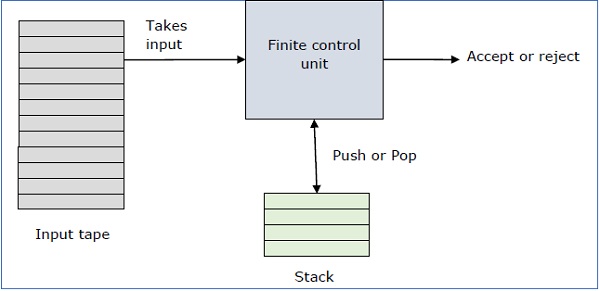
Về cơ bản một Automaton đẩy xuống là -
"Finite state machine" + "a stack"
Một ô tô tự động đẩy xuống có ba thành phần:
- một băng đầu vào,
- một đơn vị điều khiển, và
- một ngăn xếp có kích thước vô hạn.
Đầu ngăn xếp quét ký hiệu trên cùng của ngăn xếp.
Một ngăn xếp thực hiện hai hoạt động -
Push - một biểu tượng mới được thêm vào ở trên cùng.
Pop - biểu tượng trên cùng được đọc và loại bỏ.
PDA có thể đọc hoặc không đọc ký hiệu đầu vào, nhưng nó phải đọc phần trên cùng của ngăn xếp trong mọi quá trình chuyển đổi.
Một PDA có thể được mô tả chính thức là một bộ 7 (Q, ∑, S, δ, q 0 , I, F) -
Q là số trạng thái hữu hạn
∑ là bảng chữ cái đầu vào
S là ký hiệu ngăn xếp
δ là hàm chuyển tiếp: Q × (∑ ∪ {ε}) × S × Q × S *
q0là trạng thái ban đầu (q 0 ∈ Q)
I là ký hiệu đầu ngăn xếp ban đầu (I ∈ S)
F là một tập hợp các trạng thái chấp nhận (F ∈ Q)
Biểu đồ sau đây cho thấy sự chuyển đổi trong PDA từ trạng thái q 1 sang trạng thái q 2 , được gắn nhãn là a, b → c -

Điều này có nghĩa là ở trạng thái q1, nếu chúng ta gặp một chuỗi đầu vào ‘a’ và biểu tượng trên cùng của ngăn xếp là ‘b’, sau đó chúng tôi bật ‘b’, đẩy ‘c’ trên đầu ngăn xếp và chuyển sang trạng thái q2.
Các thuật ngữ liên quan đến PDA
Mô tả tức thời
Mô tả tức thời (ID) của PDA được biểu diễn bằng bộ ba (q, w, s) trong đó
q là trạng thái
w là đầu vào không tích lũy
s là nội dung ngăn xếp
Ký hiệu cửa quay
Ký hiệu "cửa quay" được sử dụng để kết nối các cặp ID đại diện cho một hoặc nhiều bước di chuyển của PDA. Quá trình chuyển đổi được biểu thị bằng ký hiệu cửa quay "⊢".
Xét một PDA (Q, ∑, S, δ, q 0 , I, F). Quá trình chuyển đổi có thể được biểu diễn toán học bằng ký hiệu cửa quay sau:
(p, aw, Tβ) ⊢ (q, w, αb)Điều này ngụ ý rằng trong khi chuyển đổi từ trạng thái p để nhà nước q, ký hiệu đầu vào ‘a’ được tiêu thụ và phần trên cùng của ngăn xếp ‘T’ được thay thế bằng một chuỗi mới ‘α’.
Note - Nếu chúng ta muốn không hoặc nhiều lần di chuyển của PDA, chúng ta phải sử dụng ký hiệu (⊢ *) cho nó.
Có hai cách khác nhau để xác định khả năng chấp nhận PDA.
Trạng thái cuối cùng được chấp nhận
Trong khả năng chấp nhận trạng thái cuối cùng, PDA chấp nhận một chuỗi khi, sau khi đọc toàn bộ chuỗi, PDA ở trạng thái cuối cùng. Từ trạng thái bắt đầu, chúng ta có thể thực hiện các bước di chuyển kết thúc ở trạng thái cuối cùng với bất kỳ giá trị ngăn xếp nào. Các giá trị ngăn xếp không liên quan miễn là chúng ta kết thúc ở trạng thái cuối cùng.
Đối với PDA (Q, ∑, S, δ, q 0 , I, F), ngôn ngữ được chấp nhận bởi tập các trạng thái cuối cùng F là:
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, x), q ∈ F}
cho bất kỳ chuỗi ngăn xếp đầu vào nào x.
Khả năng chấp nhận ngăn xếp trống
Ở đây PDA chấp nhận một chuỗi khi, sau khi đọc toàn bộ chuỗi, PDA đã làm trống ngăn xếp của nó.
Đối với PDA (Q, ∑, S, δ, q 0 , I, F), ngôn ngữ được ngăn xếp trống chấp nhận là:
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, ε), q ∈ Q}
Thí dụ
Xây dựng một PDA chấp nhận L = {0n 1n | n ≥ 0}
Giải pháp

Ngôn ngữ này chấp nhận L = {ε, 01, 0011, 000111, .............................}
Ở đây, trong ví dụ này, số lượng ‘a’ và ‘b’ phải giống nhau.
Ban đầu chúng tôi đặt một biểu tượng đặc biệt ‘$’ vào ngăn xếp trống.
Sau đó ở trạng thái q2, nếu chúng ta gặp đầu vào 0 và trên cùng là Null, chúng ta đẩy 0 vào ngăn xếp. Điều này có thể lặp lại. Và nếu chúng ta gặp đầu vào 1 và trên cùng là 0, chúng ta bật 0 này.
Sau đó ở trạng thái q3, nếu chúng ta gặp đầu vào 1 và đầu vào là 0, chúng ta bật giá trị này là 0. Điều này cũng có thể lặp lại. Và nếu chúng ta gặp đầu vào 1 và trên cùng là 0, chúng ta sẽ bật phần tử trên cùng.
Nếu ký hiệu đặc biệt '$' gặp ở trên cùng của ngăn xếp, nó sẽ xuất hiện và cuối cùng nó chuyển sang trạng thái chấp nhận q 4 .
Thí dụ
Xây dựng PDA chấp nhận L = {ww R | w = (a + b) *}
Solution

Ban đầu, chúng tôi đặt một ký hiệu đặc biệt '$' vào ngăn xếp trống. Tại trạng tháiq2, các wđang được đọc. Ở trạng tháiq3, mỗi 0 hoặc 1 sẽ xuất hiện khi khớp với đầu vào. Nếu bất kỳ đầu vào nào khác được đưa ra, PDA sẽ chuyển sang trạng thái chết. Khi chúng ta đạt đến biểu tượng đặc biệt '$', chúng ta chuyển đến trạng thái chấp nhậnq4.
Nếu một ngữ pháp G không có ngữ cảnh, chúng tôi có thể xây dựng một PDA không xác định tương đương chấp nhận ngôn ngữ được tạo ra bởi ngữ pháp không có ngữ cảnh G. Một trình phân tích cú pháp có thể được xây dựng cho ngữ phápG.
Còn nếu P là một trình tự động đẩy xuống, một ngữ pháp tương đương không có ngữ cảnh G có thể được xây dựng ở nơi
L(G) = L(P)
Trong hai chủ đề tiếp theo, chúng ta sẽ thảo luận về cách chuyển đổi từ PDA sang CFG và ngược lại.
Thuật toán tìm PDA tương ứng với CFG cho trước
Input - Một CFG, G = (V, T, P, S)
Output- PDA tương đương, P = (Q, ∑, S, δ, q 0 , I, F)
Step 1 - Chuyển đổi các sản phẩm của CFG thành GNF.
Step 2 - PDA sẽ chỉ có một trạng thái {q}.
Step 3 - Biểu tượng bắt đầu của CFG sẽ là biểu tượng bắt đầu trong PDA.
Step 4 - Tất cả các đầu cuối không phải của CFG sẽ là ký hiệu ngăn xếp của PDA và tất cả các đầu cuối của CFG sẽ là ký hiệu đầu vào của PDA.
Step 5 - Đối với mỗi lần sản xuất theo mẫu A → aX nơi a là thiết bị đầu cuối và A, X là sự kết hợp của thiết bị đầu cuối và không thiết bị đầu cuối, hãy thực hiện chuyển đổi δ (q, a, A).
Vấn đề
Xây dựng PDA từ CFG sau.
G = ({S, X}, {a, b}, P, S)
nơi sản xuất -
S → XS | ε , A → aXb | Ab | ab
Giải pháp
Để PDA tương đương,
P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)
ở đâu δ -
δ (q, ε, S) = {(q, XS), (q, ε)}
δ (q, ε, X) = {(q, aXb), (q, Xb), (q, ab)}
δ (q, a, a) = {(q, ε)}
δ (q, 1, 1) = {(q, ε)}
Thuật toán tìm CFG tương ứng với PDA cho trước
Input - Một CFG, G = (V, T, P, S)
Output- PDA tương đương, P = (Q, ∑, S, δ, q 0 , I, F) sao cho các đầu cuối của văn phạm G sẽ là {X wx | w, x ∈ Q} và trạng thái khởi đầu sẽ là Một q0, F .
Step 1- Với mọi w, x, y, z ∈ Q, m ∈ S và a, b ∈ ∑, nếu δ (w, a, ε) chứa (y, m) và (z, b, m) chứa (x, ε), thêm quy tắc sản xuất X wx → a X yz b trong ngữ pháp G.
Step 2- Với mọi w, x, y, z ∈ Q, thêm quy tắc sản xuất X wx → X wy X yx trong văn phạm G.
Step 3- Với w ∈ Q, thêm quy tắc sản xuất X ww → ε trong văn phạm G.
Phân tích cú pháp được sử dụng để lấy một chuỗi bằng cách sử dụng các quy tắc sản xuất của ngữ pháp. Nó được sử dụng để kiểm tra khả năng chấp nhận của một chuỗi. Trình biên dịch được sử dụng để kiểm tra xem một chuỗi có đúng cú pháp hay không. Một trình phân tích cú pháp lấy các đầu vào và xây dựng một cây phân tích cú pháp.
Trình phân tích cú pháp có thể có hai loại -
Top-Down Parser - Phân tích cú pháp từ trên xuống bắt đầu từ trên cùng với ký hiệu bắt đầu và dẫn xuất một chuỗi bằng cách sử dụng cây phân tích cú pháp.
Bottom-Up Parser - Phân tích cú pháp từ dưới lên bắt đầu từ dưới cùng với chuỗi và đến ký hiệu bắt đầu bằng cách sử dụng cây phân tích cú pháp.
Thiết kế trình phân tích cú pháp từ trên xuống
Để phân tích cú pháp từ trên xuống, PDA có bốn kiểu chuyển đổi sau:
Bật thiết bị đầu cuối không phải thiết bị đầu cuối ở phía bên trái của sản xuất ở trên cùng của ngăn xếp và đẩy chuỗi bên phải của nó.
Nếu biểu tượng trên cùng của ngăn xếp khớp với biểu tượng đầu vào đang được đọc, hãy bật nó lên.
Đẩy biểu tượng bắt đầu 'S' vào ngăn xếp.
Nếu chuỗi đầu vào được đọc hoàn toàn và ngăn xếp trống, hãy chuyển đến trạng thái cuối cùng 'F'.
Thí dụ
Thiết kế trình phân tích cú pháp từ trên xuống cho biểu thức "x + y * z" cho ngữ pháp G với các quy tắc sản xuất sau:
P: S → S + X | X, X → X * Y | Y, Y → (S) | Tôi
Solution
Nếu PDA là (Q, ∑, S, δ, q 0 , I, F), thì phân tích cú pháp từ trên xuống là -
(x + y * z, I) ⊢ (x + y * z, SI) ⊢ (x + y * z, S + XI) ⊢ (x + y * z, X + XI)
⊢ (x + y * z, Y + XI) ⊢ (x + y * z, x + XI) ⊢ (+ y * z, + XI) ⊢ (y * z, XI)
⊢ (y * z, X * YI) ⊢ (y * z, y * YI) ⊢ (* z, * YI) ⊢ (z, YI) ⊢ (z, zI) ⊢ (ε, I)
Thiết kế trình phân tích cú pháp từ dưới lên
Để phân tích cú pháp từ dưới lên, PDA có bốn kiểu chuyển đổi sau:
Đẩy biểu tượng đầu vào hiện tại vào ngăn xếp.
Thay thế phía bên phải của sản phẩm ở trên cùng của ngăn xếp bằng phía bên trái của nó.
Nếu phần trên cùng của phần tử ngăn xếp khớp với ký hiệu đầu vào hiện tại, hãy bật nó lên.
Nếu chuỗi đầu vào được đọc đầy đủ và chỉ khi ký hiệu bắt đầu 'S' vẫn còn trong ngăn xếp, hãy bật nó và chuyển đến trạng thái cuối cùng là 'F'.
Thí dụ
Thiết kế trình phân tích cú pháp từ trên xuống cho biểu thức "x + y * z" cho ngữ pháp G với các quy tắc sản xuất sau:
P: S → S + X | X, X → X * Y | Y, Y → (S) | Tôi
Solution
Nếu PDA là (Q, ∑, S, δ, q 0 , I, F), thì phân tích cú pháp từ dưới lên là -
(x + y * z, I) ⊢ (+ y * z, xI) ⊢ (+ y * z, YI) ⊢ (+ y * z, XI) ⊢ (+ y * z, SI)
⊢ (y * z, + SI) ⊢ (* z, y + SI) ⊢ (* z, Y + SI) ⊢ (* z, X + SI) ⊢ (z, * X + SI)
⊢ (ε, z * X + SI) ⊢ (ε, Y * X + SI) ⊢ (ε, X + SI) ⊢ (ε, SI)
Máy Turing là một thiết bị chấp nhận chấp nhận các ngôn ngữ (tập hợp có thể liệt kê một cách đệ quy) được tạo bởi các ngữ pháp loại 0. Nó được phát minh vào năm 1936 bởi Alan Turing.
Định nghĩa
Máy Turing (TM) là một mô hình toán học bao gồm một dải băng dài vô hạn được chia thành các ô mà đầu vào được đưa ra. Nó bao gồm một đầu đọc băng đầu vào. Thanh ghi trạng thái lưu trữ trạng thái của máy Turing. Sau khi đọc một ký hiệu đầu vào, nó được thay thế bằng một ký hiệu khác, trạng thái bên trong của nó bị thay đổi và nó di chuyển từ ô này sang phải hoặc trái. Nếu TM đạt đến trạng thái cuối cùng, chuỗi đầu vào được chấp nhận, nếu không sẽ bị từ chối.
Một TM có thể được mô tả chính thức là một bộ 7 (Q, X, ∑, δ, q 0 , B, F) trong đó -
Q là một tập hợp hữu hạn các trạng thái
X là bảng chữ cái băng
∑ là bảng chữ cái đầu vào
δlà một hàm chuyển tiếp; δ: Q × X → Q × X × {Left_shift, Right_shift}.
q0 là trạng thái ban đầu
B là biểu tượng trống
F là tập hợp các trạng thái cuối cùng
So sánh với automaton trước đó
Bảng sau đây cho thấy sự so sánh về cách một máy Turing khác với Finite Automaton và Pushdown Automaton.
| Máy móc | Cấu trúc dữ liệu ngăn xếp | Tính xác định? |
|---|---|---|
| Automaton hữu hạn | NA | Đúng |
| Pushdown Automaton | Cuối cùng trong lần xuất đầu tiên (LIFO) | Không |
| Máy turing | Băng vô hạn | Đúng |
Ví dụ về máy Turing
Máy turing M = (Q, X, ∑, δ, q 0 , B, F) với
- Q = {q 0 , q 1 , q 2 , q f }
- X = {a, b}
- ∑ = {1}
- q 0 = {q 0 }
- B = ký hiệu trống
- F = {q f }
δ được đưa ra bởi -
| Biểu tượng bảng chữ cái băng | Trạng thái hiện tại 'q 0 ' | Trạng thái hiện tại 'q 1 ' | Trạng thái hiện tại 'q 2 ' |
|---|---|---|---|
| a | 1Rq 1 | 1Lq 0 | 1Lq f |
| b | 1Lq 2 | 1Rq 1 | 1Rq f |
Ở đây sự chuyển đổi 1Rq 1 ngụ ý rằng ký hiệu ghi là 1, băng di chuyển sang phải, và trạng thái tiếp theo là q 1 . Tương tự, quá trình chuyển đổi 1Lq 2 ngụ ý rằng ký hiệu ghi là 1, băng di chuyển sang trái và trạng thái tiếp theo là q 2 .
Độ phức tạp về thời gian và không gian của một cỗ máy Turing
Đối với máy Turing, độ phức tạp thời gian dùng để chỉ số lần băng di chuyển khi máy được khởi tạo cho một số ký hiệu đầu vào và độ phức tạp không gian là số ô của băng được viết.
Thời gian phức tạp tất cả các chức năng hợp lý -
T(n) = O(n log n)
Độ phức tạp không gian của TM -
S(n) = O(n)
TM chấp nhận một ngôn ngữ nếu nó đi vào trạng thái cuối cùng cho bất kỳ chuỗi đầu vào w. Một ngôn ngữ có thể liệt kê một cách đệ quy (được tạo bởi ngữ pháp Kiểu-0) nếu nó được máy Turing chấp nhận.
TM quyết định một ngôn ngữ nếu nó chấp nhận nó và chuyển sang trạng thái từ chối đối với bất kỳ đầu vào nào không phải bằng ngôn ngữ đó. Một ngôn ngữ là đệ quy nếu nó được quyết định bởi máy Turing.
Có thể có một số trường hợp TM không dừng lại. TM như vậy chấp nhận ngôn ngữ, nhưng nó không quyết định nó.
Thiết kế máy Turing
Các hướng dẫn cơ bản về thiết kế máy Turing đã được giải thích dưới đây với sự trợ giúp của một số ví dụ.
ví dụ 1
Thiết kế một TM để nhận ra tất cả các chuỗi bao gồm một số lẻ của α.
Solution
Máy Turing M có thể được xây dựng bằng các bước sau:
Để cho q1 là trạng thái ban đầu.
Nếu M trong q1; khi quét α, nó chuyển sang trạng tháiq2 và viết B (chỗ trống).
Nếu M trong q2; khi quét α, nó chuyển sang trạng tháiq1 và viết B (chỗ trống).
Từ những động thái trên, chúng ta có thể thấy rằng M vào tiểu bang q1 nếu nó quét một số chẵn của α và nó đi vào trạng thái q2nếu nó quét một số lẻ của α. Vì thếq2 là trạng thái chấp nhận duy nhất.
Vì thế,
M = {{q 1 , q 2 }, {1}, {1, B}, δ, q 1 , B, {q 2 }}
trong đó δ được đưa ra bởi -
| Biểu tượng bảng chữ cái băng | Trạng thái hiện tại 'q 1 ' | Trạng thái hiện tại 'q 2 ' |
|---|---|---|
| α | BRq 2 | BRq 1 |
Ví dụ 2
Thiết kế một Máy Turing để đọc một chuỗi đại diện cho một số nhị phân và xóa tất cả các số 0 đứng đầu trong chuỗi. Tuy nhiên, nếu chuỗi chỉ bao gồm các số 0, nó sẽ giữ một số 0.
Solution
Giả sử rằng chuỗi đầu vào được kết thúc bởi một ký hiệu trống, B, ở mỗi đầu của chuỗi.
Máy Turing, M, có thể được xây dựng bằng các bước sau:
Để cho q0 là trạng thái ban đầu.
Nếu M trong q0, khi đọc 0, nó di chuyển sang phải, đi vào trạng thái q1 và xóa 0. Khi đọc 1, nó chuyển sang trạng thái q2 và di chuyển sang phải.
Nếu M trong q1, khi đọc số 0, nó di chuyển sang phải và xóa số 0, tức là nó thay thế số 0 bằng số B. Khi đến ngoài cùng bên trái 1, nó đi vàoq2và di chuyển sang phải. Nếu nó đến B, tức là, chuỗi chỉ bao gồm các số 0, nó sẽ di chuyển sang trái và đi vào trạng tháiq3.
Nếu M trong q2, khi đọc 0 hoặc 1, nó sẽ di chuyển sang phải. Khi đến B, nó di chuyển sang trái và đi vào trạng tháiq4. Điều này xác nhận rằng chuỗi chỉ bao gồm 0 và 1.
Nếu M trong q3, nó thay thế B bằng 0, di chuyển sang trái và đạt đến trạng thái cuối cùng qf.
Nếu M trong q4, khi đọc 0 hoặc 1, nó sẽ di chuyển sang trái. Khi đến đầu chuỗi, tức là khi nó đọc B, nó đạt đến trạng thái cuối cùngqf.
Vì thế,
M = {{q 0 , q 1 , q 2 , q 3 , q 4 , q f }, {0,1, B}, {1, B}, δ, q 0 , B, {q f }}
trong đó δ được đưa ra bởi -
| Biểu tượng bảng chữ cái băng | Trạng thái hiện tại 'q 0 ' | Trạng thái hiện tại 'q 1 ' | Trạng thái hiện tại 'q 2 ' | Trạng thái hiện tại 'q 3 ' | Trạng thái hiện tại 'q 4 ' |
|---|---|---|---|---|---|
| 0 | BRq 1 | BRq 1 | ORq 2 | - | OLq 4 |
| 1 | 1Rq 2 | 1Rq 2 | 1Rq 2 | - | 1Lq 4 |
| B | BRq 1 | BLq 3 | BLq 4 | OLq f | BRq f |
Máy Turing nhiều băng có nhiều băng trong đó mỗi băng được truy cập bằng một đầu riêng biệt. Mỗi đầu có thể di chuyển độc lập với các đầu khác. Ban đầu đầu vào nằm trên băng 1 và những đầu vào khác trống. Lúc đầu, băng đầu tiên bị chiếm bởi đầu vào và các băng khác được giữ trống. Tiếp theo, máy đọc các ký hiệu liên tiếp dưới đầu của nó và TM in một ký hiệu trên mỗi băng và di chuyển các đầu của nó.

Máy Turing nhiều băng có thể được mô tả chính thức như một bộ 6 bộ (Q, X, B, δ, q 0 , F) trong đó -
Q là một tập hợp hữu hạn các trạng thái
X là bảng chữ cái băng
B là biểu tượng trống
δ là một quan hệ về trạng thái và biểu tượng trong đó
δ: Q × X k → Q × (X × {Left_shift, Right_shift, No_shift}) k
ở đâu có k số lượng băng
q0 là trạng thái ban đầu
F là tập hợp các trạng thái cuối cùng
Note - Mỗi máy Turing nhiều băng đều có một máy Turing một băng tương đương.
Máy Turing nhiều rãnh, một loại cụ thể của Máy Turing nhiều băng, chứa nhiều rãnh nhưng chỉ một đầu băng đọc và ghi trên tất cả các rãnh. Ở đây, một đầu băng đơn đọc n ký hiệu từntheo dõi ở một bước. Nó chấp nhận các ngôn ngữ có thể liệt kê đệ quy giống như một Máy Turing băng đơn một rãnh thông thường chấp nhận.
Máy Turing nhiều rãnh có thể được mô tả chính thức là một bộ 6 bộ (Q, X, ∑, δ, q 0 , F) trong đó -
Q là một tập hợp hữu hạn các trạng thái
X là bảng chữ cái băng
∑ là bảng chữ cái đầu vào
δ là một quan hệ về trạng thái và biểu tượng trong đó
δ (Q i , [a 1 , a 2 , a 3 , ....]) = (Q j , [b 1 , b 2 , b 3 , ....], Left_shift hoặc Right_shift)
q0 là trạng thái ban đầu
F là tập hợp các trạng thái cuối cùng
Note - Đối với mọi Máy Turing đơn S, có một Máy Turing đa rãnh tương đương M như vậy mà L(S) = L(M).
Trong Máy điều chỉnh không xác định, đối với mọi trạng thái và biểu tượng, có một nhóm hành động mà TM có thể thực hiện. Vì vậy, ở đây các chuyển đổi không mang tính xác định. Tính toán của Máy điều chỉnh không xác định là một cây cấu hình có thể đạt được từ cấu hình bắt đầu.
Một đầu vào được chấp nhận nếu có ít nhất một nút của cây là cấu hình chấp nhận, nếu không thì nó không được chấp nhận. Nếu tất cả các nhánh của cây tính toán dừng lại trên tất cả các đầu vào, Máy điều chỉnh không xác định được gọi làDecider và nếu đối với một số đầu vào, tất cả các nhánh đều bị từ chối thì đầu vào cũng bị từ chối.
Máy Turing không xác định có thể được định nghĩa chính thức là một bộ 6 bộ (Q, X, ∑, δ, q 0 , B, F) trong đó -
Q là một tập hợp hữu hạn các trạng thái
X là bảng chữ cái băng
∑ là bảng chữ cái đầu vào
δ là một hàm chuyển tiếp;
δ: Q × X → P (Q × X × {Left_shift, Right_shift}).
q0 là trạng thái ban đầu
B là biểu tượng trống
F là tập hợp các trạng thái cuối cùng
Một Máy Turing có băng bán vô hạn có đầu bên trái nhưng không có đầu bên phải. Đầu bên trái được giới hạn bằng một điểm đánh dấu kết thúc.

Nó là một băng hai track -
Upper track - Nó đại diện cho các ô ở bên phải của vị trí đầu ban đầu.
Lower track - Nó đại diện cho các ô bên trái của vị trí đầu ban đầu theo thứ tự ngược lại.
Chuỗi đầu vào có độ dài vô hạn ban đầu được viết trên băng trong các ô băng liền nhau.
Máy bắt đầu từ trạng thái ban đầu q0và phần đầu quét từ điểm đánh dấu cuối bên trái 'End'. Trong mỗi bước, nó đọc ký hiệu trên băng dưới đầu nó. Nó viết một ký hiệu mới trên ô băng đó và sau đó nó di chuyển đầu sang trái hoặc phải một ô băng. Một chức năng chuyển tiếp xác định các hành động được thực hiện.
Nó có hai trạng thái đặc biệt được gọi là accept state và reject state. Nếu tại bất kỳ thời điểm nào nó chuyển sang trạng thái được chấp nhận, đầu vào được chấp nhận và nếu nó đi vào trạng thái từ chối, đầu vào sẽ bị TM từ chối. Trong một số trường hợp, nó tiếp tục chạy vô hạn mà không được chấp nhận hoặc bị từ chối đối với một số ký hiệu đầu vào nhất định.
Note - Máy Turing có băng bán vô hạn tương đương với máy Turing tiêu chuẩn.
Một máy tự động có giới hạn tuyến tính là một máy Turing đa rãnh không xác định với một dải băng có độ dài hữu hạn nhất định.
Length = function (Length of the initial input string, constant c)
Đây,
Memory information ≤ c × Input information
Việc tính toán bị giới hạn trong vùng giới hạn không đổi. Bảng chữ cái đầu vào chứa hai ký hiệu đặc biệt đóng vai trò là điểm đánh dấu cuối bên trái và điểm đánh dấu cuối bên phải, có nghĩa là các chuyển đổi không di chuyển sang trái của điểm đánh dấu cuối bên trái hoặc sang bên phải của điểm đánh dấu cuối bên phải của băng.
Một ô tô tự động giới hạn tuyến tính có thể được định nghĩa là một bộ 8 (Q, X, ∑, q 0 , ML, MR, δ, F) trong đó -
Q là một tập hợp hữu hạn các trạng thái
X là bảng chữ cái băng
∑ là bảng chữ cái đầu vào
q0 là trạng thái ban đầu
ML là điểm đánh dấu cuối bên trái
MRlà điểm đánh dấu cuối bên phải nơi M R ≠ M L
δ là một hàm chuyển đổi ánh xạ từng cặp (trạng thái, biểu tượng băng) sang (trạng thái, biểu tượng băng, Hằng số 'c') trong đó c có thể là 0 hoặc +1 hoặc -1
F là tập hợp các trạng thái cuối cùng

Automaton giới hạn tuyến tính xác định luôn là context-sensitive và automaton giới hạn tuyến tính với ngôn ngữ trống là undecidable..
Một ngôn ngữ được gọi là Decidable hoặc là Recursive nếu có một máy Turing chấp nhận và tạm dừng trên mọi chuỗi đầu vào w. Mọi ngôn ngữ quyết định đều là Turing-Acceptable.

Một vấn đề quyết định P là quyết định nếu ngôn ngữ L trong số tất cả các trường hợp có cho P là quyết định.
Đối với ngôn ngữ có thể phân giải, đối với mỗi chuỗi đầu vào, TM sẽ tạm dừng ở trạng thái chấp nhận hoặc từ chối như được mô tả trong sơ đồ sau:

ví dụ 1
Tìm hiểu xem vấn đề sau có phải là giải pháp hay không:
Một số 'm' có phải là số nguyên tố không?
Giải pháp
Số nguyên tố = {2, 3, 5, 7, 11, 13, ………… ..}
Chia số ‘m’ bởi tất cả các số từ '2' đến '√m' bắt đầu từ '2'.
Nếu bất kỳ con số nào trong số này tạo ra phần dư là 0, thì nó chuyển sang "Trạng thái bị từ chối", nếu không nó sẽ chuyển sang "Trạng thái được chấp nhận". Vì vậy, ở đây câu trả lời có thể là 'Có' hoặc 'Không'.
Hence, it is a decidable problem.
Ví dụ 2
Cho một ngôn ngữ thông thường L và chuỗi w, làm thế nào chúng tôi có thể kiểm tra nếu w ∈ L?
Giải pháp
Lấy DFA chấp nhận L và kiểm tra xem w được chấp nhận

Một số vấn đề khó giải quyết hơn là -
- DFA có chấp nhận ngôn ngữ trống không?
- L 1 ∩ L 2 = ∅ có phải là tập hợp chính quy không?
Note -
Nếu một ngôn ngữ L là quyết định, sau đó bổ sung của nó L' cũng có thể quyết định
Nếu một ngôn ngữ có thể phân biệt được thì sẽ có một điều tra viên cho nó.
Đối với một ngôn ngữ không thể quyết định, không có Máy Turing nào chấp nhận ngôn ngữ đó và đưa ra quyết định cho mọi chuỗi đầu vào w(TM có thể đưa ra quyết định cho một số chuỗi đầu vào). Một vấn đề quyết địnhP được gọi là "không thể quyết định" nếu ngôn ngữ L trong số tất cả các trường hợp có cho Pkhông phải là quyết định. Các ngôn ngữ không thể quyết định không phải là ngôn ngữ đệ quy, nhưng đôi khi, chúng có thể là ngôn ngữ có thể liệt kê một cách đệ quy.

Thí dụ
- Sự cố dừng của máy Turing
- Vấn đề tử vong
- Vấn đề ma trận sinh tử
- Bài báo vấn đề, v.v.
Input - Một máy Turing và một chuỗi đầu vào w.
Problem - Máy Turing có hoàn thành tính toán chuỗi không wtrong một số bước hữu hạn? Câu trả lời phải là có hoặc không.
Proof- Lúc đầu, chúng tôi sẽ cho rằng tồn tại một cỗ máy Turing như vậy để giải quyết vấn đề này và sau đó chúng tôi sẽ cho thấy nó đang mâu thuẫn với chính nó. Chúng tôi sẽ gọi máy Turing này làHalting machinetạo ra 'có' hoặc 'không' trong một khoảng thời gian hữu hạn. Nếu máy tạm dừng kết thúc trong một khoảng thời gian hữu hạn, kết quả đầu ra là "có", ngược lại là "không". Sau đây là sơ đồ khối của máy tạm dừng -

Bây giờ chúng tôi sẽ thiết kế một inverted halting machine (HM)’ như -
Nếu H trả về CÓ, sau đó lặp lại mãi mãi.
Nếu H trả về KHÔNG, sau đó dừng lại.
Sau đây là sơ đồ khối của 'Máy dừng ngược' -

Hơn nữa, một chiếc máy (HM)2 đầu vào nào chính nó được xây dựng như sau:
- Nếu (HM) 2 dừng trên đầu vào, lặp lại mãi mãi.
- Khác, dừng lại.
Ở đây, chúng tôi đã có một mâu thuẫn. Do đó, vấn đề tạm dừng làundecidable.
Định lý Rice nói rằng bất kỳ thuộc tính ngữ nghĩa không tầm thường nào của một ngôn ngữ được máy Turing nhận ra là không thể quyết định được. Thuộc tính, P, là ngôn ngữ của tất cả các máy Turing thỏa mãn thuộc tính đó.
Định nghĩa chính thức
Nếu P là một thuộc tính không tầm thường và ngôn ngữ chứa thuộc tính, L p , được máy Turing M nhận dạng, thì L p = {<M> | L (M) ∈ P} không xác định được.
Mô tả và Thuộc tính
Thuộc tính của ngôn ngữ, P, chỉ đơn giản là một tập hợp các ngôn ngữ. Nếu ngôn ngữ nào thuộc P (L ∈ P), thì nói rằng L thỏa mãn tính chất P.
A property is called to be trivial if either it is not satisfied by any recursively enumerable languages, or if it is satisfied by all recursively enumerable languages.
A non-trivial property is satisfied by some recursively enumerable languages and are not satisfied by others. Formally speaking, in a non-trivial property, where L ∈ P, both the following properties hold:
Property 1 − There exists Turing Machines, M1 and M2 that recognize the same language, i.e. either ( <M1>, <M2> ∈ L ) or ( <M1>,<M2> ∉ L )
Property 2 − There exists Turing Machines M1 and M2, where M1 recognizes the language while M2 does not, i.e. <M1> ∈ L and <M2> ∉ L
Proof
Suppose, a property P is non-trivial and φ ∈ P.
Since, P is non-trivial, at least one language satisfies P, i.e., L(M0) ∈ P , ∋ Turing Machine M0.
Let, w be an input in a particular instant and N is a Turing Machine which follows −
On input x
- Run M on w
- If M does not accept (or doesn't halt), then do not accept x (or do not halt)
- If M accepts w then run M0 on x. If M0 accepts x, then accept x.
A function that maps an instance ATM = {<M,w>| M accepts input w} to a N such that
- If M accepts w and N accepts the same language as M0, Then L(M) = L(M0) ∈ p
- If M does not accept w and N accepts φ, Then L(N) = φ ∉ p
Since ATM is undecidable and it can be reduced to Lp, Lp is also undecidable.
The Post Correspondence Problem (PCP), introduced by Emil Post in 1946, is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x1, x2, x3,………, xn)
N = (y1, y2, y3,………, yn)
We can say that there is a Post Correspondence Solution, if for some i1,i2,………… ik, where 1 ≤ ij ≤ n, the condition xi1 …….xik = yi1 …….yik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | Abb | aa | aaa |
| N | Bba | aaa | aa |
Here,
x2x1x3 = ‘aaabbaaa’
and y2y1y3 = ‘aaabbaaa’
We can see that
x2x1x3 = y2y1y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 2
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | ab | bab | bbaaa |
| N | a | ba | bab |
In this case, there is no solution because −
| x2x1x3 | ≠ | y2y1y3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.