Automaton hữu hạn không xác định

Trong NDFA, đối với một ký hiệu đầu vào cụ thể, máy có thể di chuyển đến bất kỳ tổ hợp trạng thái nào trong máy. Nói cách khác, không thể xác định chính xác trạng thái mà máy chuyển động. Do đó, nó được gọi làNon-deterministic Automaton. Vì nó có số trạng thái hữu hạn, máy được gọi làNon-deterministic Finite Machine hoặc là Non-deterministic Finite Automaton.

Định nghĩa chính thức về NDFA

NDFA có thể được biểu diễn bằng 5 bộ (Q, ∑, δ, q ₀ , F) trong đó -

Q là một tập hợp hữu hạn các trạng thái.
∑ là một tập hợp hữu hạn các ký hiệu được gọi là các bảng chữ cái.
δlà hàm chuyển tiếp trong đó δ: Q × ∑ → 2 ^Q

(Ở đây, tập hợp lũy thừa của Q (2 ^Q ) đã được lấy vì trong trường hợp NDFA, từ một trạng thái, chuyển đổi có thể xảy ra thành bất kỳ sự kết hợp nào của Q trạng thái)
q₀là trạng thái ban đầu mà từ đó bất kỳ đầu vào nào được xử lý (q ₀ ∈ Q).
F là tập hợp các trạng thái / trạng thái cuối cùng của Q (F ⊆ Q).

Biểu diễn đồ họa của một NDFA: (giống như DFA)

NDFA được biểu diễn bằng các đồ thị được gọi là biểu đồ trạng thái.

Các đỉnh đại diện cho các trạng thái.
Các cung được gắn nhãn với bảng chữ cái đầu vào hiển thị các chuyển đổi.
Trạng thái ban đầu được biểu thị bằng một cung tới trống.
Trạng thái cuối cùng được biểu thị bằng các vòng tròn đôi.

Example

Cho một tự động hữu hạn không xác định là →

Q = {a, b, c}
∑ = {0, 1}
q ₀ = {a}
F = {c}

Hàm chuyển đổi δ như hình dưới đây -

Trạng thái hiện tại	Trạng thái tiếp theo cho đầu vào 0	Trạng thái tiếp theo cho đầu vào 1
a	a, b	b
b	c	AC
c	b, c	c

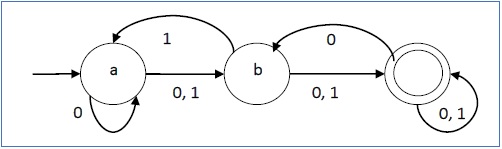
Biểu diễn đồ họa của nó sẽ như sau:

DFA so với NDFA

Bảng sau liệt kê sự khác biệt giữa DFA và NDFA.

DFA	NDFA
Việc chuyển đổi từ một trạng thái là một trạng thái tiếp theo cụ thể cho mỗi ký hiệu đầu vào. Do đó nó được gọi là xác định .	Việc chuyển đổi từ một trạng thái có thể là nhiều trạng thái tiếp theo cho mỗi ký hiệu đầu vào. Do đó nó được gọi là không xác định .
Chuyển đổi chuỗi trống không được nhìn thấy trong DFA.	NDFA cho phép chuyển đổi chuỗi trống.
Bẻ khóa ngược được cho phép trong DFA	Trong NDFA, không phải lúc nào cũng có thể bẻ khóa ngược.
Yêu cầu nhiều không gian hơn.	Yêu cầu ít không gian hơn.
Một chuỗi được DFA chấp nhận, nếu nó chuyển sang trạng thái cuối cùng.	Một chuỗi được NDFA chấp nhận, nếu ít nhất một trong tất cả các chuyển đổi có thể kết thúc ở trạng thái cuối cùng.

Bộ chấp nhận, bộ phân loại và bộ chuyển đổi

Người chấp nhận (Công nhận)

Một automaton tính toán một hàm Boolean được gọi là acceptor. Tất cả các trạng thái của bộ chấp nhận là chấp nhận hoặc từ chối các đầu vào được cung cấp cho nó.

Phân loại

A classifier có nhiều hơn hai trạng thái cuối cùng và nó cho một đầu ra duy nhất khi nó kết thúc.

Đầu dò

Một Automaton tạo ra đầu ra dựa trên đầu vào hiện tại và / hoặc trạng thái trước đó được gọi là transducer. Đầu dò có thể có hai loại -

Mealy Machine - Đầu ra phụ thuộc cả vào trạng thái hiện tại và đầu vào hiện tại.
Moore Machine - Đầu ra chỉ phụ thuộc vào trạng thái hiện tại.

Khả năng chấp nhận của DFA và NDFA

Một chuỗi được chấp nhận bởi DFA / NDFA và DFA / NDFA bắt đầu ở trạng thái ban đầu kết thúc ở trạng thái chấp nhận (bất kỳ trạng thái cuối cùng nào) sau khi đọc toàn bộ chuỗi.

Chuỗi S được chấp nhận bởi DFA / NDFA (Q, ∑, δ, q ₀ , F), iff

δ*(q₀, S) ∈ F

Ngôn ngữ L được chấp nhận bởi DFA / NDFA là

{S | S ∈ ∑* and δ*(q₀, S) ∈ F}

Chuỗi S ′ không được chấp nhận bởi DFA / NDFA (Q, ∑, δ, q ₀ , F), iff

δ*(q₀, S′) ∉ F

Ngôn ngữ L ′ không được DFA / NDFA chấp nhận (Bổ sung ngôn ngữ L được chấp nhận) là

{S | S ∈ ∑* and δ*(q₀, S) ∉ F}

Example

Chúng ta hãy xem xét DFA được thể hiện trong Hình 1.3. Từ DFA, các chuỗi được chấp nhận có thể được rút ra.