Truyền thông qua vệ tinh - Cơ học quỹ đạo

Chúng ta biết rằng đường đi của vệ tinh quay quanh trái đất được gọi là orbit. Đường dẫn này có thể được biểu diễn bằng các ký hiệu toán học. Cơ học quỹ đạo là nghiên cứu về chuyển động của các vệ tinh có trong quỹ đạo. Vì vậy, chúng ta có thể dễ dàng hiểu các hoạt động trong không gian với kiến thức về chuyển động quỹ đạo.

Yếu tố quỹ đạo

Yếu tố quỹ đạo là các tham số, giúp ích cho việc mô tả chuyển động quỹ đạo của vệ tinh. Sau đây làorbital elements.

Bán trục chính
Eccentricity
Có nghĩa là bất thường
Lập luận về sự nguy hiểm
Inclination
Sự thăng hoa bên phải của nút tăng dần

Sáu yếu tố quỹ đạo trên xác định quỹ đạo của vệ tinh trái đất. Do đó, có thể dễ dàng phân biệt một vệ tinh này với các vệ tinh khác dựa trên các giá trị của các phần tử quỹ đạo.

Bán trục chính

Chiều dài của Semi-major axis (a)xác định kích thước quỹ đạo của vệ tinh. Nó là một nửa của trục chính. Điều này chạy từ trung tâm qua tiêu điểm đến cạnh của hình elip. Vì vậy, nó là bán kính của quỹ đạo tại hai điểm xa nhất của quỹ đạo.

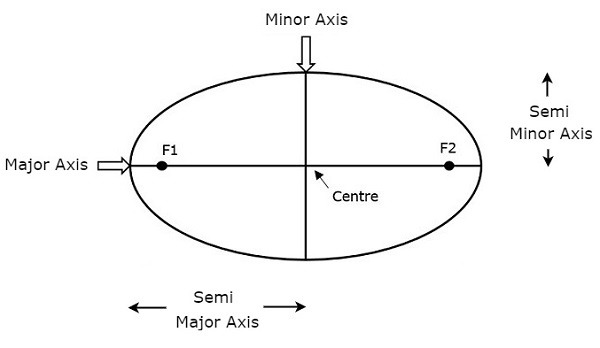
Cả hai trục bán chính và trục bán phụ được biểu diễn trong hình trên. Chiều dài của bánmajor axis (a) không chỉ xác định kích thước quỹ đạo của vệ tinh, mà còn là khoảng thời gian của cuộc cách mạng.

Nếu coi quỹ đạo tròn là trường hợp đặc biệt thì độ dài của bán trục chính sẽ bằng radius của quỹ đạo tròn đó.

Độ lệch tâm

Giá trị của Eccentricity (e)sửa hình dạng quỹ đạo của vệ tinh. Tham số này chỉ ra độ lệch của hình dạng quỹ đạo so với một đường tròn hoàn hảo.

Nếu độ dài của nửa trục chính và nửa trục nhỏ của quỹ đạo hình elip là a & b, thì biểu thức toán học cho eccentricity (e) sẽ là

$$ e = \ frac {\ sqrt {a ^ 2 - b ^ 2}} {a} $$

Giá trị của độ lệch tâm của quỹ đạo tròn là zero, vì cả a & b đều bằng nhau. Trong khi đó, giá trị độ lệch tâm của quỹ đạo hình elip nằm giữa 0 và 1.

Sau figure hiển thị các quỹ đạo vệ tinh khác nhau cho các giá trị độ lệch tâm (e) khác nhau

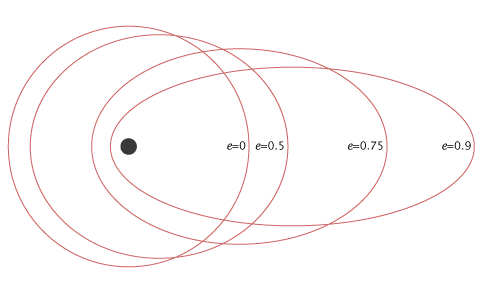
Trong hình trên, quỹ đạo vệ tinh ứng với giá trị độ lệch tâm (e) bằng 0 là quỹ đạo tròn. Và, ba quỹ đạo vệ tinh còn lại có dạng elip tương ứng với các giá trị độ lệch tâm (e) 0,5, 0,75 và 0,9.

Có nghĩa là bất thường

Đối với vệ tinh, điểm gần Trái đất nhất được gọi là Perigee. Mean anomaly (M) cho giá trị trung bình của vị trí góc của vệ tinh có tham chiếu đến perigee.

Nếu quỹ đạo là hình tròn thì dị thường Mean cho vị trí góc của vệ tinh trên quỹ đạo. Tuy nhiên, nếu quỹ đạo là hình elip thì việc tính toán vị trí chính xác là rất khó. Khi đó, Mean dị thường được sử dụng như một bước trung gian.

Lập luận của Perigee

Quỹ đạo vệ tinh cắt mặt phẳng xích đạo tại hai điểm. Điểm đầu tiên được gọi làdescending node, nơi vệ tinh đi từ Bắc bán cầu sang Nam bán cầu. Điểm thứ hai được gọi làascending node, nơi vệ tinh đi từ Nam bán cầu sang Bắc bán cầu.

Argument of perigee (ω)là góc giữa nút tăng dần và nút. Nếu cả nút perigee và nút tăng dần đều tồn tại tại cùng một điểm, thì đối số của perigee sẽ là 0 độ

Đối số của perigee được đo trong mặt phẳng quỹ đạo tại tâm trái đất theo hướng chuyển động của vệ tinh.

Độ nghiêng

Góc giữa mặt phẳng quỹ đạo và mặt phẳng xích đạo của trái đất được gọi là inclination (i). Nó được đo tại nút tăng dần với hướng từ đông sang bắc. Vì vậy, độ nghiêng xác định hướng của quỹ đạo bằng cách coi đường xích đạo của trái đất là tham chiếu.

Có bốn loại quỹ đạo dựa trên góc nghiêng.

Equatorial orbit - Góc nghiêng là 0 độ hoặc 180 độ.
Polar orbit - Góc nghiêng 90 độ.
Prograde orbit - Góc nghiêng nằm trong khoảng từ 0 đến 90 độ.
Retrograde orbit - Góc nghiêng nằm trong khoảng 90 - 180 độ.

Tăng lên bên phải của nút Tăng dần

Chúng ta biết rằng ascending node là điểm, nơi vệ tinh băng qua mặt phẳng xích đạo trong khi đi từ Nam bán cầu sang Bắc bán cầu.

Tăng lên bên phải của nút tăng dần (Ω)là góc giữa đường Bạch Dương và nút đi lên theo hướng đông trong mặt phẳng xích đạo. Bạch dương còn được gọi là vernal và phân.

Vệ tinh của ground tracklà đường đi trên bề mặt Trái đất, nằm chính xác bên dưới quỹ đạo của nó. Đường trên mặt đất của vệ tinh có thể có một số dạng khác nhau tùy thuộc vào giá trị của các phần tử quỹ đạo.

Phương trình quỹ đạo

Trong phần này, chúng ta hãy thảo luận về các phương trình liên quan đến chuyển động của quỹ đạo.

Lực lượng hành động trên vệ tinh

Một vệ tinh khi quay quanh trái đất thì nó phải chịu một lực kéo từ trái đất do lực hút của trái đất. Lực lượng này được gọi làCentripetal force(F ₁ ) vì lực này hướng vệ tinh về phía nó.

Về mặt toán học, Centripetal force(F ₁ ) tác động lên vệ tinh do trái đất có thể được viết là

$$ F_ {1} = \ frac {GMm} {R ^ 2} $$

Ở đâu,

Glà hằng số hấp dẫn phổ quát và nó bằng 6,673 x 10 ^-11 N ∙ m ² / kg ² .
Mlà khối lượng của trái đất và nó bằng 5,98 x 10 ²⁴ Kg.
m là khối lượng của vệ tinh.
R là khoảng cách từ vệ tinh đến tâm Trái đất.

Một vệ tinh, khi quay quanh trái đất, nó phải chịu một lực kéo từ mặt trời và mặt trăng do lực hấp dẫn của chúng. Lực lượng này được gọi làCentrifugal force(F ₂ ) vì lực này hướng vệ tinh ra xa trái đất.

Về mặt toán học, Centrifugal force(F ₂ ) tác động lên vệ tinh có thể được viết là

$$ F_ {2} = \ frac {mv ^ 2} {R} $$

Ở đâu, v là vận tốc quỹ đạo của vệ tinh.

Vận tốc quỹ đạo

Vận tốc quỹ đạo của vệ tinh là vận tốc mà vệ tinh quay quanh trái đất. Vệ tinh không bị lệch khỏi quỹ đạo của nó và chuyển động với vận tốc nhất định trong quỹ đạo đó, khi cả lực Hướng tâm và Lực ly tâm làbalance lẫn nhau.

Vì thế, equateLực hướng tâm (F ₁ ) và Lực ly tâm (F ₂ ).

$$ \ frac {GMm} {R ^ 2} = \ frac {mv ^ 2} {R} $$

$$ => \ frac {GM} {R} = v ^ 2 $$

$$ => v = \ sqrt {\ frac {GM} {R}} $$

Do đó, orbital velocity của vệ tinh là

$$ v = \ sqrt {\ frac {GM} {R}} $$

Ở đâu,