TensorFlow - Khái niệm cơ bản

Trong chương này, chúng ta sẽ tìm hiểu những kiến thức cơ bản về TensorFlow. Chúng ta sẽ bắt đầu bằng cách tìm hiểu cấu trúc dữ liệu của tensor.

Cấu trúc dữ liệu căng thẳng

Tensors được sử dụng làm cấu trúc dữ liệu cơ bản trong ngôn ngữ TensorFlow. Tensors đại diện cho các cạnh kết nối trong bất kỳ sơ đồ luồng nào được gọi là Biểu đồ luồng dữ liệu. Tensors được định nghĩa là mảng hoặc danh sách nhiều chiều.

Độ căng được xác định bởi ba tham số sau:

Cấp

Đơn vị kích thước được mô tả trong tensor được gọi là thứ hạng. Nó xác định số kích thước của tensor. Thứ hạng của một tensor có thể được mô tả là thứ tự hoặc thứ n của một tensor được xác định.

Hình dạng

Số lượng hàng và cột cùng nhau xác định hình dạng của Tensor.

Kiểu

Kiểu mô tả kiểu dữ liệu được gán cho các phần tử của Tensor.

Người dùng cần xem xét các hoạt động sau để xây dựng Tensor:

Xây dựng một mảng n chiều
Chuyển đổi mảng n-chiều.

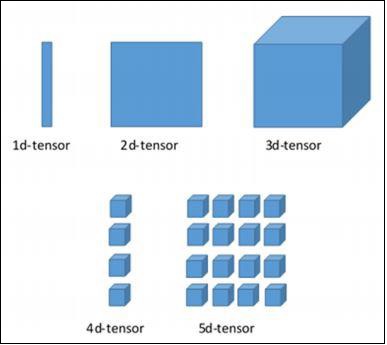
Các kích thước khác nhau của TensorFlow

TensorFlow bao gồm nhiều thứ nguyên khác nhau. Các kích thước được mô tả ngắn gọn bên dưới:

Tensor một chiều

Teo một chiều là một cấu trúc mảng bình thường bao gồm một bộ giá trị của cùng một kiểu dữ liệu.

Declaration

>>> import numpy as np
>>> tensor_1d = np.array([1.3, 1, 4.0, 23.99])
>>> print tensor_1d

Việc triển khai với đầu ra được hiển thị trong ảnh chụp màn hình bên dưới -

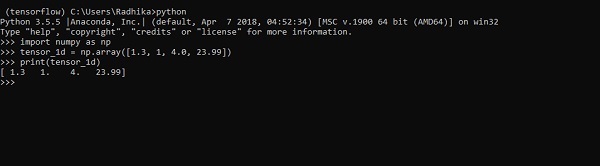
Việc lập chỉ mục các phần tử giống như danh sách Python. Phần tử đầu tiên bắt đầu với chỉ số 0; để in các giá trị thông qua chỉ mục, tất cả những gì bạn cần làm là đề cập đến số chỉ mục.

>>> print tensor_1d[0]
1.3
>>> print tensor_1d[2]
4.0

Hai chiều căng

Chuỗi các mảng được sử dụng để tạo ra "các tenxơ hai chiều".

Việc tạo ra các tenxơ hai chiều được mô tả dưới đây:

Sau đây là cú pháp hoàn chỉnh để tạo mảng hai chiều:

>>> import numpy as np
>>> tensor_2d = np.array([(1,2,3,4),(4,5,6,7),(8,9,10,11),(12,13,14,15)])
>>> print(tensor_2d)
[[ 1 2 3 4]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
>>>

Các phần tử cụ thể của bộ căng hai chiều có thể được theo dõi với sự trợ giúp của số hàng và số cột được chỉ định làm số chỉ mục.

>>> tensor_2d[3][2]
14

Xử lý và thao tác kéo căng

Trong phần này, chúng ta sẽ tìm hiểu về Xử lý và Thao tác kéo căng.

Để bắt đầu, chúng ta hãy xem xét đoạn mã sau:

import tensorflow as tf
import numpy as np

matrix1 = np.array([(2,2,2),(2,2,2),(2,2,2)],dtype = 'int32')
matrix2 = np.array([(1,1,1),(1,1,1),(1,1,1)],dtype = 'int32')

print (matrix1)
print (matrix2)

matrix1 = tf.constant(matrix1)
matrix2 = tf.constant(matrix2)
matrix_product = tf.matmul(matrix1, matrix2)
matrix_sum = tf.add(matrix1,matrix2)
matrix_3 = np.array([(2,7,2),(1,4,2),(9,0,2)],dtype = 'float32')
print (matrix_3)

matrix_det = tf.matrix_determinant(matrix_3)
with tf.Session() as sess:
   result1 = sess.run(matrix_product)
   result2 = sess.run(matrix_sum)
   result3 = sess.run(matrix_det)

print (result1)
print (result2)
print (result3)

Output

Đoạn mã trên sẽ tạo ra kết quả sau:

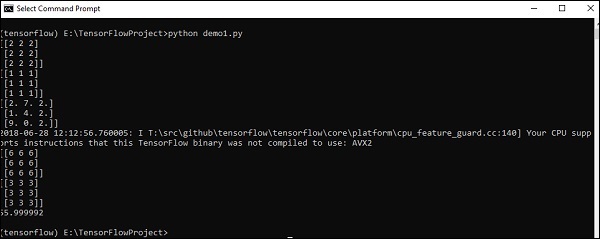
Giải trình

Chúng tôi đã tạo các mảng nhiều chiều trong mã nguồn trên. Bây giờ, điều quan trọng là phải hiểu rằng chúng tôi đã tạo biểu đồ và phiên để quản lý các Tensors và tạo ra đầu ra phù hợp. Với sự trợ giúp của đồ thị, chúng ta có đầu ra xác định các phép tính toán học giữa các Tensors.