TensorFlow - Cơ sở Toán học
Điều quan trọng là phải hiểu các khái niệm toán học cần thiết cho TensorFlow trước khi tạo ứng dụng cơ bản trong TensorFlow. Toán học được coi là trái tim của bất kỳ thuật toán học máy nào. Với sự trợ giúp của các khái niệm cốt lõi của Toán học, một giải pháp cho thuật toán học máy cụ thể được xác định.
Véc tơ
Một mảng số, liên tục hoặc rời rạc, được định nghĩa là một vectơ. Các thuật toán học máy xử lý các vectơ có độ dài cố định để tạo ra đầu ra tốt hơn.
Các thuật toán học máy xử lý dữ liệu đa chiều nên vectơ đóng một vai trò quan trọng.

Biểu diễn bằng hình ảnh của mô hình vectơ như hình dưới đây -
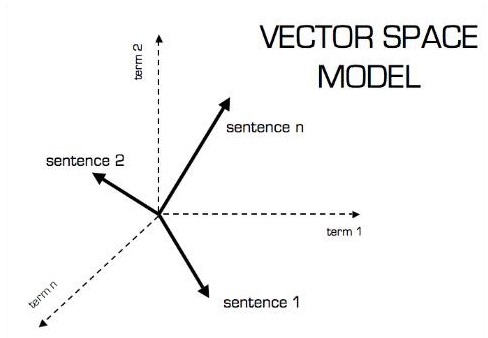
Vô hướng
Vô hướng có thể được định nghĩa là vectơ một chiều. Vô hướng là những cái chỉ bao gồm độ lớn và không có hướng. Với vô hướng, chúng ta chỉ quan tâm đến độ lớn.
Ví dụ về vô hướng bao gồm các thông số về cân nặng và chiều cao của trẻ em.
Ma trận
Ma trận có thể được định nghĩa là các mảng đa chiều, được sắp xếp theo định dạng hàng và cột. Kích thước của ma trận được xác định bởi độ dài hàng và độ dài cột. Hình sau cho thấy biểu diễn của bất kỳ ma trận cụ thể nào.
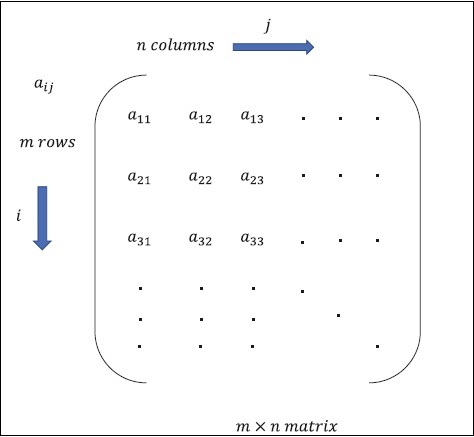
Hãy xem xét ma trận có hàng “m” và cột “n” như đã đề cập ở trên, biểu diễn ma trận sẽ được xác định là “ma trận m * n” cũng xác định độ dài của ma trận.
Tính toán toán học
Trong phần này, chúng ta sẽ tìm hiểu về các phép tính toán học khác nhau trong TensorFlow.
Phép cộng ma trận
Có thể cộng hai hoặc nhiều ma trận nếu các ma trận có cùng thứ nguyên. Phép cộng ngụ ý bổ sung từng phần tử theo vị trí đã cho.
Hãy xem xét ví dụ sau để hiểu cách hoạt động của phép cộng ma trận:
$$ Ví dụ: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: A + B = \ begin {bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \ end {bmatrix} = \ begin {bmatrix} 6 & 8 \\ 10 & 12 \ end {bmatrix} $$
Phép trừ ma trận
Phép trừ ma trận hoạt động theo kiểu tương tự như phép cộng hai ma trận. Người dùng có thể trừ hai ma trận miễn là các thứ nguyên bằng nhau.
$$ Ví dụ: A- \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B- \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: AB - \ begin {bmatrix} 1-5 & 2-6 \\ 3-7 & 4-8 \ end {bmatrix} - \ begin {bmatrix} -4 & -4 \\ - 4 & -4 \ end {bmatrix} $$
Phép nhân ma trận
Để hai ma trận A m * n và B p * q có thể nhân được, n nên bằng p. Ma trận kết quả là -
C m * q
$$ A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} $$
$$ c_ {11} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 1 \ times5 + 2 \ times7 = 19 \: c_ {12} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 1 \ times6 + 2 \ times8 = 22 $$
$$ c_ {21} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 3 \ times5 + 4 \ times7 = 43 \: c_ {22} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 3 \ times6 + 4 \ times8 = 50 $$
$$ C = \ begin {bmatrix} c_ {11} & c_ {12} \\ c_ {21} & c_ {22} \ end {bmatrix} = \ begin {bmatrix} 19 & 22 \\ 43 & 50 \ end {bmatrix} $$
Chuyển vị của ma trận
Chuyển vị của ma trận A, m * n thường được biểu diễn bằng AT (chuyển vị) n * m và thu được bằng cách chuyển các vectơ cột thành vectơ hàng.
$$ Ví dụ: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \: then \: A ^ {T} \ begin {bmatrix} 1 & 3 \\ 2 & 4 \ end { bmatrix} $$
Tích chấm của vectơ
Bất kỳ vectơ nào có chiều n có thể được biểu diễn dưới dạng ma trận v = R ^ n * 1.
$$ v_ {1} = \ begin {bmatrix} v_ {11} \\ v_ {12} \\\ cdot \\\ cdot \\\ cdot \\ v_ {1n} \ end {bmatrix} v_ {2} = \ begin {bmatrix} v_ {21} \\ v_ {22} \\\ cdot \\\ cdot \\\ cdot \\ v_ {2n} \ end {bmatrix} $$
Tích chấm của hai vectơ là tổng tích của các thành phần tương ứng - Các thành phần có cùng chiều và có thể được biểu thị bằng
$$ v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = v_2 ^ Tv_ {1} = v_ {11} v_ {21} + v_ {12} v_ {22} + \ cdot \ cdot + v_ {1n} v_ {2n} = \ displaystyle \ sum \ limit_ {k = 1} ^ n v_ {1k} v_ {2k} $$
Ví dụ về tích số chấm của vectơ được đề cập dưới đây:
$$ Ví dụ: v_ {1} = \ begin {bmatrix} 1 \\ 2 \\ 3 \ end {bmatrix} v_ {2} = \ begin {bmatrix} 3 \\ 5 \\ - 1 \ end {bmatrix} v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = 1 \ times3 + 2 \ times5-3 \ times1 = 10 $$