TensorFlow - Hướng dẫn nhanh
TensorFlow là một thư viện hoặc khung phần mềm, được nhóm Google thiết kế để triển khai các khái niệm học máy và học sâu một cách dễ dàng nhất. Nó kết hợp đại số tính toán của các kỹ thuật tối ưu hóa để dễ dàng tính toán nhiều biểu thức toán học.
Trang web chính thức của TensorFlow được đề cập dưới đây:
www.tensorflow.org
Bây giờ chúng ta hãy xem xét các tính năng quan trọng sau của TensorFlow:
Nó bao gồm một tính năng xác định, tối ưu hóa và tính toán các biểu thức toán học một cách dễ dàng với sự trợ giúp của các mảng đa chiều được gọi là tensors.
Nó bao gồm hỗ trợ lập trình của mạng nơ-ron sâu và các kỹ thuật máy học.
Nó bao gồm một tính năng tính toán có khả năng mở rộng cao với các bộ dữ liệu khác nhau.
TensorFlow sử dụng điện toán GPU, tự động hóa việc quản lý. Nó cũng bao gồm một tính năng độc đáo là tối ưu hóa cùng một bộ nhớ và dữ liệu được sử dụng.
Tại sao TensorFlow lại phổ biến như vậy?
TensorFlow được ghi chép đầy đủ và bao gồm nhiều thư viện máy học. Nó cung cấp một số chức năng và phương pháp quan trọng cho cùng một.
TensorFlow còn được gọi là sản phẩm của “Google”. Nó bao gồm một loạt các thuật toán học máy và học sâu. TensorFlow có thể đào tạo và chạy các mạng thần kinh sâu để phân loại chữ số viết tay, nhận dạng hình ảnh, nhúng từ và tạo các mô hình trình tự khác nhau.
Để cài đặt TensorFlow, điều quan trọng là phải cài đặt “Python” trong hệ thống của bạn. Phiên bản Python 3.4+ được coi là tốt nhất để bắt đầu với cài đặt TensorFlow.
Xem xét các bước sau để cài đặt TensorFlow trong hệ điều hành Windows.
Step 1 - Xác minh phiên bản python đang được cài đặt.
Step 2- Người dùng có thể chọn bất kỳ cơ chế nào để cài đặt TensorFlow trong hệ thống. Chúng tôi đề xuất "pip" và "Anaconda". Pip là một lệnh được sử dụng để thực thi và cài đặt các mô-đun bằng Python.
Trước khi cài đặt TensorFlow, chúng ta cần cài đặt Anaconda framework trong hệ thống của mình.
Sau khi cài đặt thành công, hãy kiểm tra dấu nhắc lệnh thông qua lệnh “conda”. Việc thực thi lệnh được hiển thị bên dưới:
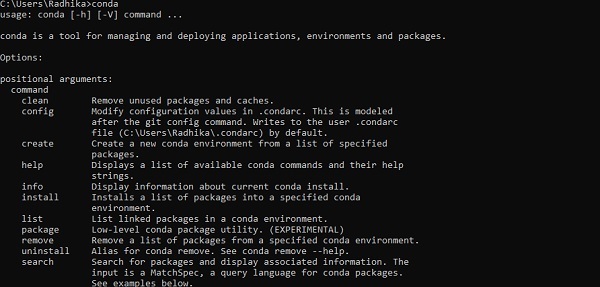
Step 3 - Thực hiện lệnh sau để khởi tạo cài đặt TensorFlow -
conda create --name tensorflow python = 3.5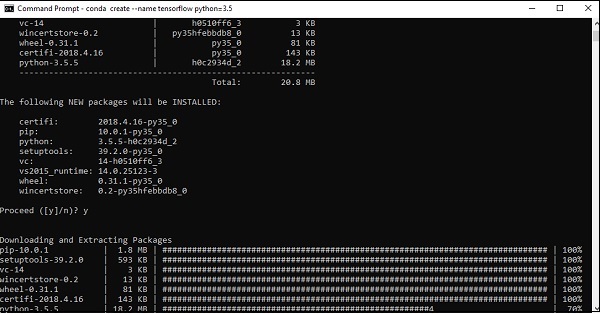
Nó tải xuống các gói cần thiết cần thiết để thiết lập TensorFlow.
Step 4 - Sau khi thiết lập môi trường thành công, điều quan trọng là phải kích hoạt mô-đun TensorFlow.
activate tensorflow
Step 5- Sử dụng pip để cài đặt “Tensorflow” trong hệ thống. Lệnh được sử dụng để cài đặt được đề cập như sau:
pip install tensorflowVà,
pip install tensorflow-gpu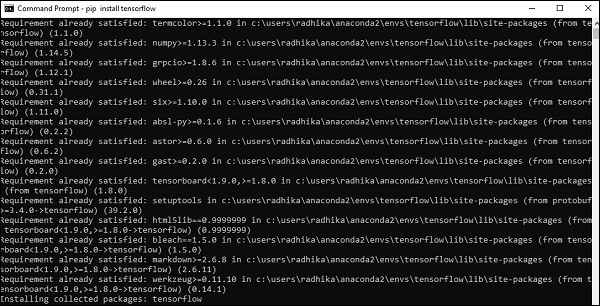
Sau khi cài đặt thành công, điều quan trọng là phải biết thực thi chương trình mẫu của TensorFlow.
Ví dụ sau giúp chúng ta hiểu cách tạo chương trình cơ bản “Hello World” trong TensorFlow.
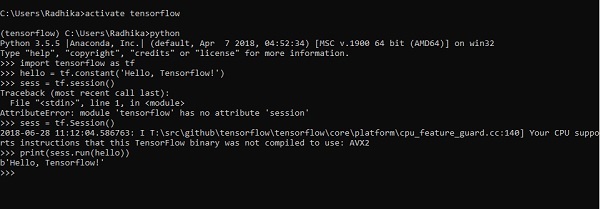
Mã để triển khai chương trình đầu tiên được đề cập dưới đây:
>> activate tensorflow
>> python (activating python shell)
>> import tensorflow as tf
>> hello = tf.constant(‘Hello, Tensorflow!’)
>> sess = tf.Session()
>> print(sess.run(hello))Trí tuệ nhân tạo bao gồm quá trình mô phỏng trí thông minh của con người bằng máy móc và các hệ thống máy tính đặc biệt. Các ví dụ về trí tuệ nhân tạo bao gồm học tập, suy luận và tự sửa chữa. Các ứng dụng của AI bao gồm nhận dạng giọng nói, hệ thống chuyên gia, nhận dạng hình ảnh và thị giác máy.
Học máy là nhánh của trí tuệ nhân tạo, liên quan đến các hệ thống và thuật toán có thể học bất kỳ dữ liệu và mẫu dữ liệu mới nào.
Chúng ta hãy tập trung vào biểu đồ Venn được đề cập bên dưới để hiểu các khái niệm về học máy và học sâu.
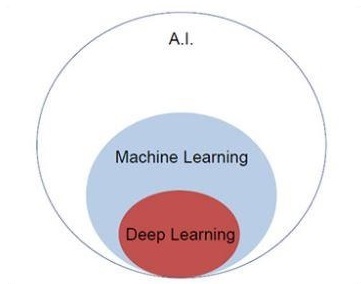
Học máy bao gồm một phần của học máy và học sâu là một phần của học máy. Khả năng của chương trình tuân theo các khái niệm học máy là cải thiện hiệu suất của dữ liệu quan sát được. Động cơ chính của việc chuyển đổi dữ liệu là nâng cao kiến thức để đạt được kết quả tốt hơn trong tương lai, cung cấp đầu ra gần với đầu ra mong muốn cho hệ thống cụ thể đó. Học máy bao gồm “nhận dạng mẫu” bao gồm khả năng nhận dạng các mẫu trong dữ liệu.
Các mẫu phải được đào tạo để hiển thị đầu ra theo cách mong muốn.
Học máy có thể được đào tạo theo hai cách khác nhau -
- Đào tạo có giám sát
- Đào tạo không giám sát
Học tập có giám sát
Học tập có giám sát hoặc đào tạo có giám sát bao gồm một thủ tục trong đó tập hợp đào tạo được đưa ra làm đầu vào cho hệ thống, trong đó, mỗi ví dụ được gắn nhãn với một giá trị đầu ra mong muốn. Việc đào tạo kiểu này được thực hiện bằng cách sử dụng tối thiểu hóa một hàm tổn thất cụ thể, hàm này biểu thị lỗi đầu ra đối với hệ thống đầu ra mong muốn.
Sau khi hoàn thành đào tạo, độ chính xác của mỗi mô hình được đo đối với các ví dụ rời rạc từ tập huấn luyện, còn được gọi là tập hợp lệ.
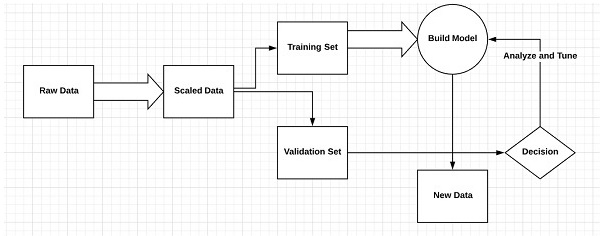
Ví dụ tốt nhất để minh họa cho “Học tập có giám sát” là với một loạt các bức ảnh được cung cấp kèm theo thông tin. Tại đây, người dùng có thể đào tạo một người mẫu để nhận ra các bức ảnh mới.
Học tập không giám sát
Trong học tập không có giám sát hoặc đào tạo không có giám sát, hãy bao gồm các ví dụ đào tạo, các ví dụ này không được hệ thống gắn nhãn cho lớp chúng thuộc về. Hệ thống tìm kiếm dữ liệu có chung đặc điểm và thay đổi chúng dựa trên các đặc điểm kiến thức nội bộ. Loại thuật toán học tập này về cơ bản được sử dụng trong các bài toán phân cụm.
Ví dụ tốt nhất để minh họa “Học không giám sát” là với một loạt ảnh không có thông tin và mô hình đào tạo người dùng với phân loại và phân cụm. Loại thuật toán huấn luyện này hoạt động với các giả định khi không có thông tin nào được đưa ra.

Điều quan trọng là phải hiểu các khái niệm toán học cần thiết cho TensorFlow trước khi tạo ứng dụng cơ bản trong TensorFlow. Toán học được coi là trái tim của bất kỳ thuật toán học máy nào. Với sự trợ giúp của các khái niệm cốt lõi của Toán học, một giải pháp cho thuật toán học máy cụ thể được xác định.
Véc tơ
Một mảng số, liên tục hoặc rời rạc, được định nghĩa là một vectơ. Các thuật toán học máy xử lý các vectơ có độ dài cố định để tạo ra đầu ra tốt hơn.
Các thuật toán học máy xử lý dữ liệu đa chiều nên vectơ đóng một vai trò quan trọng.

Biểu diễn bằng hình ảnh của mô hình vectơ như hình dưới đây -
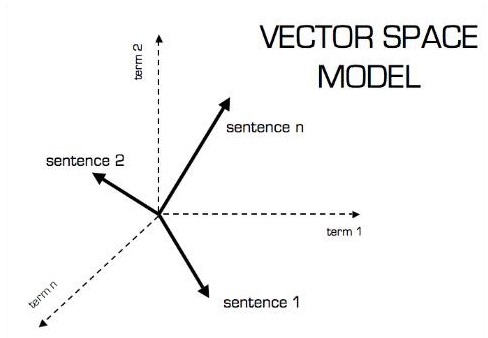
Vô hướng
Vô hướng có thể được định nghĩa là vectơ một chiều. Vô hướng là những cái chỉ bao gồm độ lớn và không có hướng. Với vô hướng, chúng ta chỉ quan tâm đến độ lớn.
Ví dụ về vô hướng bao gồm các thông số về cân nặng và chiều cao của trẻ em.
Ma trận
Ma trận có thể được định nghĩa là các mảng đa chiều, được sắp xếp theo định dạng hàng và cột. Kích thước của ma trận được xác định bởi độ dài hàng và độ dài cột. Hình sau cho thấy biểu diễn của bất kỳ ma trận cụ thể nào.
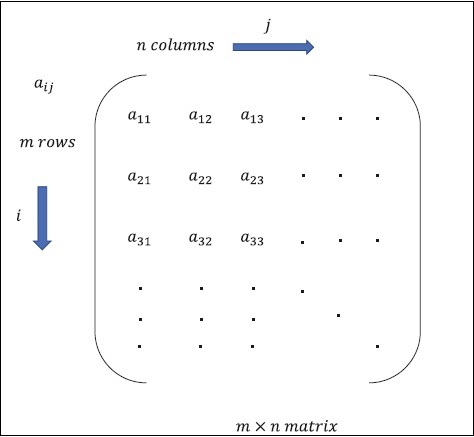
Hãy xem xét ma trận có hàng “m” và cột “n” như đã đề cập ở trên, biểu diễn ma trận sẽ được xác định là “ma trận m * n” cũng xác định độ dài của ma trận.
Tính toán toán học
Trong phần này, chúng ta sẽ tìm hiểu về các phép tính toán học khác nhau trong TensorFlow.
Phép cộng ma trận
Có thể cộng hai hoặc nhiều ma trận nếu các ma trận có cùng thứ nguyên. Phép cộng ngụ ý bổ sung từng phần tử theo vị trí đã cho.
Hãy xem xét ví dụ sau để hiểu cách hoạt động của phép cộng ma trận:
$$ Ví dụ: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: A + B = \ begin {bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \ end {bmatrix} = \ begin {bmatrix} 6 & 8 \\ 10 & 12 \ end {bmatrix} $$
Phép trừ ma trận
Phép trừ ma trận hoạt động theo kiểu tương tự như phép cộng hai ma trận. Người dùng có thể trừ hai ma trận miễn là các thứ nguyên bằng nhau.
$$ Ví dụ: A- \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B- \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: AB - \ begin {bmatrix} 1-5 & 2-6 \\ 3-7 & 4-8 \ end {bmatrix} - \ begin {bmatrix} -4 & -4 \\ - 4 & -4 \ end {bmatrix} $$
Phép nhân ma trận
Để hai ma trận A m * n và B p * q có thể nhân được, n nên bằng p. Ma trận kết quả là -
C m * q
$$ A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} $$
$$ c_ {11} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 1 \ times5 + 2 \ times7 = 19 \: c_ {12} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 1 \ times6 + 2 \ times8 = 22 $$
$$ c_ {21} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 3 \ times5 + 4 \ times7 = 43 \: c_ {22} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 3 \ times6 + 4 \ times8 = 50 $$
$$ C = \ begin {bmatrix} c_ {11} & c_ {12} \\ c_ {21} & c_ {22} \ end {bmatrix} = \ begin {bmatrix} 19 & 22 \\ 43 & 50 \ end {bmatrix} $$
Chuyển vị của ma trận
Chuyển vị của ma trận A, m * n thường được biểu diễn bằng AT (chuyển vị) n * m và thu được bằng cách chuyển các vectơ cột thành vectơ hàng.
$$ Ví dụ: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \: then \: A ^ {T} \ begin {bmatrix} 1 & 3 \\ 2 & 4 \ end { bmatrix} $$
Tích chấm của vectơ
Bất kỳ vectơ nào có chiều n có thể được biểu diễn dưới dạng ma trận v = R ^ n * 1.
$$ v_ {1} = \ begin {bmatrix} v_ {11} \\ v_ {12} \\\ cdot \\\ cdot \\\ cdot \\ v_ {1n} \ end {bmatrix} v_ {2} = \ begin {bmatrix} v_ {21} \\ v_ {22} \\\ cdot \\\ cdot \\\ cdot \\ v_ {2n} \ end {bmatrix} $$
Tích chấm của hai vectơ là tổng tích của các thành phần tương ứng - Các thành phần có cùng chiều và có thể được biểu thị bằng
$$ v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = v_2 ^ Tv_ {1} = v_ {11} v_ {21} + v_ {12} v_ {22} + \ cdot \ cdot + v_ {1n} v_ {2n} = \ displaystyle \ sum \ limit_ {k = 1} ^ n v_ {1k} v_ {2k} $$
Ví dụ về tích số chấm của vectơ được đề cập dưới đây:
$$ Ví dụ: v_ {1} = \ begin {bmatrix} 1 \\ 2 \\ 3 \ end {bmatrix} v_ {2} = \ begin {bmatrix} 3 \\ 5 \\ - 1 \ end {bmatrix} v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = 1 \ times3 + 2 \ times5-3 \ times1 = 10 $$
Trí tuệ nhân tạo là một trong những xu hướng phổ biến nhất trong thời gian gần đây. Học máy và học sâu tạo thành trí tuệ nhân tạo. Biểu đồ Venn được hiển thị bên dưới giải thích mối quan hệ của học máy và học sâu -

Học máy
Học máy là nghệ thuật khoa học giúp máy tính hoạt động theo các thuật toán được thiết kế và lập trình. Nhiều nhà nghiên cứu cho rằng học máy là cách tốt nhất để đạt được tiến bộ đối với AI ở cấp độ con người. Học máy bao gồm các loại mẫu sau
- Mô hình học tập có giám sát
- Mô hình học tập không giám sát
Học kĩ càng
Học sâu là một lĩnh vực con của học máy, trong đó các thuật toán liên quan được lấy cảm hứng từ cấu trúc và chức năng của não được gọi là mạng thần kinh nhân tạo.
Tất cả giá trị ngày nay của học sâu là thông qua học có giám sát hoặc học từ dữ liệu và thuật toán được gắn nhãn.
Mỗi thuật toán trong học sâu trải qua cùng một quá trình. Nó bao gồm một hệ thống phân cấp của phép biến đổi phi tuyến của đầu vào có thể được sử dụng để tạo ra một mô hình thống kê dưới dạng đầu ra.
Hãy xem xét các bước sau để xác định quy trình Học máy
- Xác định các tập dữ liệu có liên quan và chuẩn bị chúng để phân tích.
- Chọn loại thuật toán để sử dụng
- Xây dựng mô hình phân tích dựa trên thuật toán được sử dụng.
- Đào tạo mô hình trên các tập dữ liệu thử nghiệm, sửa đổi nó khi cần thiết.
- Chạy mô hình để tạo điểm kiểm tra.
Sự khác biệt giữa Học máy và Học sâu
Trong phần này, chúng ta sẽ tìm hiểu về sự khác biệt giữa Học máy và Học sâu.
Số lượng dữ liệu
Máy học hoạt động với lượng lớn dữ liệu. Nó cũng hữu ích cho một lượng nhỏ dữ liệu. Mặt khác, học sâu hoạt động hiệu quả nếu lượng dữ liệu tăng nhanh. Biểu đồ sau đây cho thấy hoạt động của học máy và học sâu với lượng dữ liệu:
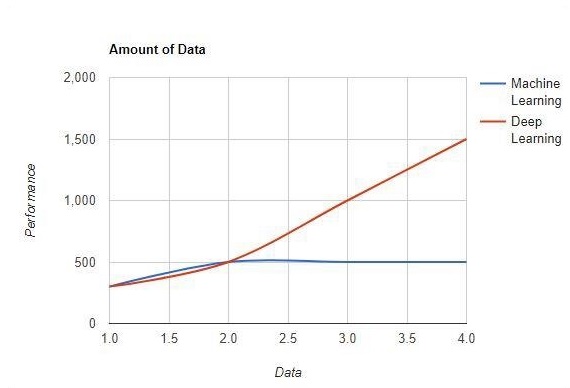
Phụ thuộc phần cứng
Các thuật toán học sâu được thiết kế để phụ thuộc nhiều vào các máy cao cấp không giống như các thuật toán học máy truyền thống. Các thuật toán học sâu thực hiện một số phép toán nhân ma trận, đòi hỏi một lượng lớn phần cứng hỗ trợ.
Kỹ thuật tính năng
Kỹ thuật tính năng là quá trình đưa kiến thức miền vào các tính năng cụ thể để giảm độ phức tạp của dữ liệu và làm cho các mẫu có thể nhìn thấy được đối với các thuật toán học mà nó hoạt động.
Ví dụ - Các mẫu máy học truyền thống tập trung vào pixel và các thuộc tính khác cần thiết cho quy trình kỹ thuật tính năng. Các thuật toán học sâu tập trung vào các tính năng cấp cao từ dữ liệu. Nó làm giảm nhiệm vụ phát triển trình trích xuất tính năng mới của mọi vấn đề mới.
Cách tiếp cận giải quyết vấn đề
Các thuật toán học máy truyền thống tuân theo một quy trình chuẩn để giải quyết vấn đề. Nó chia vấn đề thành nhiều phần, giải quyết từng phần và kết hợp chúng để có được kết quả cần thiết. Học sâu tập trung vào việc giải quyết vấn đề từ đầu đến cuối thay vì chia chúng thành nhiều phần.
Thời gian thực hiện
Thời gian thực thi là khoảng thời gian cần thiết để đào tạo một thuật toán. Học sâu đòi hỏi nhiều thời gian để đào tạo vì nó bao gồm rất nhiều tham số, mất nhiều thời gian hơn bình thường. Thuật toán học máy tương đối yêu cầu ít thời gian thực thi hơn.
Khả năng diễn giải
Khả năng diễn giải là yếu tố chính để so sánh giữa các thuật toán học máy và học sâu. Lý do chính là học sâu vẫn được quan tâm trước khi sử dụng nó trong ngành công nghiệp.
Các ứng dụng của Học máy và Học sâu
Trong phần này, chúng ta sẽ tìm hiểu về các ứng dụng khác nhau của Học máy và Học sâu.
Thị giác máy tính được sử dụng để nhận dạng khuôn mặt và đánh dấu điểm danh thông qua dấu vân tay hoặc nhận dạng phương tiện thông qua biển số.
Thông tin Lấy từ các công cụ tìm kiếm như tìm kiếm văn bản cho tìm kiếm hình ảnh.
Tiếp thị qua email tự động với xác định mục tiêu cụ thể.
Chẩn đoán y tế về khối u ung thư hoặc xác định bất thường của bất kỳ bệnh mãn tính nào.
Xử lý ngôn ngữ tự nhiên cho các ứng dụng như gắn thẻ ảnh. Ví dụ tốt nhất để giải thích tình huống này được sử dụng trong Facebook.
Quảng cáo trực tuyến.
Xu hướng tương lai
Với xu hướng ngày càng tăng của việc sử dụng khoa học dữ liệu và học máy trong ngành, việc khắc sâu học máy vào doanh nghiệp của họ sẽ trở nên quan trọng đối với mỗi tổ chức.
Học sâu đang trở nên quan trọng hơn học máy. Học sâu đang được chứng minh là một trong những kỹ thuật tốt nhất trong hoạt động biểu diễn hiện đại.
Học máy và học sâu sẽ tỏ ra có lợi trong lĩnh vực nghiên cứu và học thuật.
Phần kết luận
Trong bài viết này, chúng tôi đã có một cái nhìn tổng quan về học máy và học sâu với các hình ảnh minh họa và sự khác biệt cũng tập trung vào các xu hướng trong tương lai. Nhiều ứng dụng AI sử dụng các thuật toán máy học chủ yếu để thúc đẩy khả năng tự phục vụ, tăng năng suất của tác nhân và quy trình làm việc đáng tin cậy hơn. Các thuật toán học máy và học sâu bao gồm một triển vọng thú vị cho nhiều doanh nghiệp và các nhà lãnh đạo ngành.
Trong chương này, chúng ta sẽ tìm hiểu những kiến thức cơ bản về TensorFlow. Chúng ta sẽ bắt đầu bằng cách tìm hiểu cấu trúc dữ liệu của tensor.
Cấu trúc dữ liệu căng thẳng
Tensors được sử dụng làm cấu trúc dữ liệu cơ bản trong ngôn ngữ TensorFlow. Tensors đại diện cho các cạnh kết nối trong bất kỳ sơ đồ luồng nào được gọi là Biểu đồ luồng dữ liệu. Tensors được định nghĩa là mảng hoặc danh sách nhiều chiều.
Độ căng được xác định bởi ba tham số sau:
Cấp
Đơn vị kích thước được mô tả trong tensor được gọi là thứ hạng. Nó xác định số kích thước của tensor. Thứ hạng của một tensor có thể được mô tả là thứ tự hoặc thứ n của một tensor được xác định.
Hình dạng
Số lượng hàng và cột cùng nhau xác định hình dạng của Tensor.
Kiểu
Kiểu mô tả kiểu dữ liệu được gán cho các phần tử của Tensor.
Người dùng cần xem xét các hoạt động sau để xây dựng Tensor:
- Xây dựng một mảng n chiều
- Chuyển đổi mảng n-chiều.
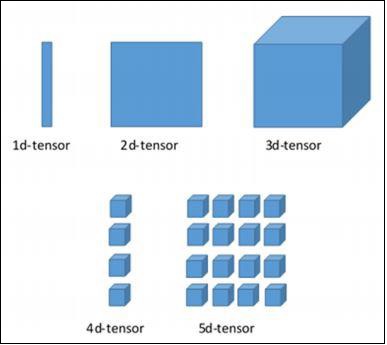
Các kích thước khác nhau của TensorFlow
TensorFlow bao gồm nhiều thứ nguyên khác nhau. Các kích thước được mô tả ngắn gọn bên dưới:
Tensor một chiều
Teo một chiều là một cấu trúc mảng bình thường bao gồm một bộ giá trị của cùng một kiểu dữ liệu.
Declaration
>>> import numpy as np
>>> tensor_1d = np.array([1.3, 1, 4.0, 23.99])
>>> print tensor_1dViệc triển khai với đầu ra được hiển thị trong ảnh chụp màn hình bên dưới -
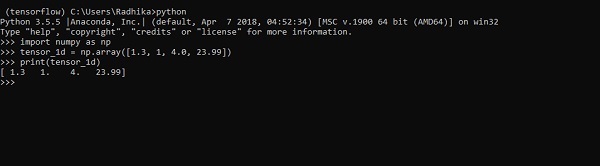
Việc lập chỉ mục các phần tử giống như danh sách Python. Phần tử đầu tiên bắt đầu với chỉ số 0; để in các giá trị thông qua chỉ mục, tất cả những gì bạn cần làm là đề cập đến số chỉ mục.
>>> print tensor_1d[0]
1.3
>>> print tensor_1d[2]
4.0
Hai chiều căng
Chuỗi các mảng được sử dụng để tạo ra "các tenxơ hai chiều".
Việc tạo ra các tenxơ hai chiều được mô tả dưới đây:

Sau đây là cú pháp hoàn chỉnh để tạo mảng hai chiều:
>>> import numpy as np
>>> tensor_2d = np.array([(1,2,3,4),(4,5,6,7),(8,9,10,11),(12,13,14,15)])
>>> print(tensor_2d)
[[ 1 2 3 4]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
>>>Các phần tử cụ thể của bộ căng hai chiều có thể được theo dõi với sự trợ giúp của số hàng và số cột được chỉ định làm số chỉ mục.
>>> tensor_2d[3][2]
14
Xử lý và thao tác kéo căng
Trong phần này, chúng ta sẽ tìm hiểu về Xử lý và Thao tác kéo căng.
Để bắt đầu, chúng ta hãy xem xét đoạn mã sau:
import tensorflow as tf
import numpy as np
matrix1 = np.array([(2,2,2),(2,2,2),(2,2,2)],dtype = 'int32')
matrix2 = np.array([(1,1,1),(1,1,1),(1,1,1)],dtype = 'int32')
print (matrix1)
print (matrix2)
matrix1 = tf.constant(matrix1)
matrix2 = tf.constant(matrix2)
matrix_product = tf.matmul(matrix1, matrix2)
matrix_sum = tf.add(matrix1,matrix2)
matrix_3 = np.array([(2,7,2),(1,4,2),(9,0,2)],dtype = 'float32')
print (matrix_3)
matrix_det = tf.matrix_determinant(matrix_3)
with tf.Session() as sess:
result1 = sess.run(matrix_product)
result2 = sess.run(matrix_sum)
result3 = sess.run(matrix_det)
print (result1)
print (result2)
print (result3)Output
Đoạn mã trên sẽ tạo ra kết quả sau:
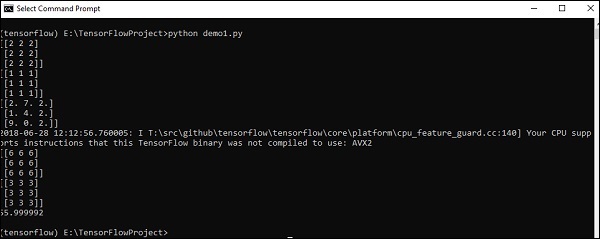
Giải trình
Chúng tôi đã tạo các mảng nhiều chiều trong mã nguồn trên. Bây giờ, điều quan trọng là phải hiểu rằng chúng tôi đã tạo biểu đồ và phiên để quản lý các Tensors và tạo ra đầu ra phù hợp. Với sự trợ giúp của đồ thị, chúng ta có đầu ra xác định các phép tính toán học giữa các Tensors.
Sau khi hiểu các khái niệm học máy, giờ đây chúng ta có thể chuyển trọng tâm sang các khái niệm học sâu. Học sâu là một bộ phận của học máy và được các nhà nghiên cứu coi là một bước quan trọng trong những thập kỷ gần đây. Các ví dụ về triển khai học sâu bao gồm các ứng dụng như nhận dạng hình ảnh và nhận dạng giọng nói.
Sau đây là hai loại mạng nơ-ron sâu quan trọng:
- Mạng thần kinh chuyển đổi
- Mạng thần kinh tái diễn
Trong chương này, chúng ta sẽ tập trung vào CNN, Mạng thần kinh chuyển đổi.
Mạng thần kinh chuyển đổi
Mạng Neural Convolutions được thiết kế để xử lý dữ liệu thông qua nhiều lớp mảng. Loại mạng nơ-ron này được sử dụng trong các ứng dụng như nhận dạng hình ảnh hoặc nhận dạng khuôn mặt. Sự khác biệt cơ bản giữa CNN và bất kỳ mạng nơ-ron thông thường nào khác là CNN nhận đầu vào dưới dạng mảng hai chiều và hoạt động trực tiếp trên hình ảnh thay vì tập trung vào việc trích xuất tính năng mà các mạng nơ-ron khác tập trung vào.
Cách tiếp cận chủ đạo của CNN bao gồm các giải pháp cho các vấn đề về nhận dạng. Các công ty hàng đầu như Google và Facebook đã đầu tư vào nghiên cứu và phát triển theo hướng các dự án công nhận để hoàn thành các hoạt động với tốc độ nhanh hơn.
Một mạng nơ-ron tích tụ sử dụng ba ý tưởng cơ bản:
- Các trường tương ứng địa phương
- Convolution
- Pooling
Hãy để chúng tôi hiểu những ý tưởng này một cách chi tiết.
CNN sử dụng các mối tương quan không gian tồn tại trong dữ liệu đầu vào. Mỗi lớp đồng thời của mạng nơ-ron kết nối một số nơ-ron đầu vào. Vùng cụ thể này được gọi là trường tiếp nhận cục bộ. Trường tiếp nhận cục bộ tập trung vào các tế bào thần kinh ẩn. Các nơ-ron ẩn xử lý dữ liệu đầu vào bên trong trường được đề cập không nhận ra những thay đổi bên ngoài ranh giới cụ thể.
Sau đây là biểu đồ biểu diễn tạo các trường tương ứng cục bộ:
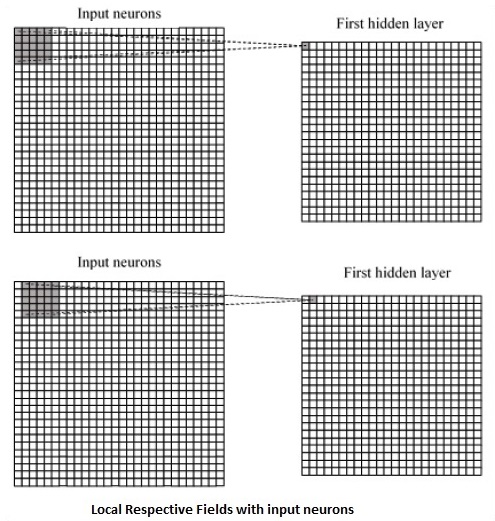
Nếu chúng ta quan sát sự biểu diễn ở trên, mỗi kết nối học được một trọng số của nơ-ron ẩn với một kết nối liên quan với chuyển động từ lớp này sang lớp khác. Tại đây, các tế bào thần kinh riêng lẻ thực hiện sự thay đổi theo thời gian. Quá trình này được gọi là "tích chập".
Ánh xạ các kết nối từ lớp đầu vào đến bản đồ đối tượng ẩn được định nghĩa là "trọng số được chia sẻ" và thiên vị bao gồm được gọi là "thiên vị được chia sẻ".
CNN hoặc mạng nơ-ron tích hợp sử dụng các lớp gộp, là các lớp, được định vị ngay sau khai báo CNN. Nó lấy dữ liệu đầu vào từ người dùng dưới dạng một bản đồ tính năng xuất phát từ các mạng phức hợp và chuẩn bị một bản đồ tính năng cô đọng. Việc gộp các lớp giúp tạo các lớp với các nơ-ron của các lớp trước đó.
Triển khai TensorFlow của CNN
Trong phần này, chúng ta sẽ tìm hiểu về việc triển khai TensorFlow của CNN. Các bước, yêu cầu thực hiện và kích thước thích hợp của toàn bộ mạng, như được minh họa bên dưới -
Step 1 - Bao gồm các mô-đun cần thiết cho TensorFlow và các mô-đun tập dữ liệu, cần thiết để tính toán mô hình CNN.
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_dataStep 2 - Khai báo một hàm được gọi là run_cnn(), bao gồm các tham số và biến tối ưu hóa khác nhau với khai báo các trình giữ chỗ dữ liệu. Các biến tối ưu hóa này sẽ khai báo mẫu đào tạo.
def run_cnn():
mnist = input_data.read_data_sets("MNIST_data/", one_hot = True)
learning_rate = 0.0001
epochs = 10
batch_size = 50Step 3 - Trong bước này, chúng tôi sẽ khai báo các trình giữ chỗ dữ liệu huấn luyện với các tham số đầu vào - cho 28 x 28 pixel = 784. Đây là dữ liệu hình ảnh phẳng được lấy từ mnist.train.nextbatch().
Chúng tôi có thể định hình lại tensor theo yêu cầu của chúng tôi. Giá trị đầu tiên (-1) cho hàm biết để định hình động thứ nguyên đó dựa trên lượng dữ liệu được truyền vào nó. Hai kích thước giữa được đặt thành kích thước hình ảnh (tức là 28 x 28).
x = tf.placeholder(tf.float32, [None, 784])
x_shaped = tf.reshape(x, [-1, 28, 28, 1])
y = tf.placeholder(tf.float32, [None, 10])Step 4 - Bây giờ điều quan trọng là tạo một số lớp phức hợp -
layer1 = create_new_conv_layer(x_shaped, 1, 32, [5, 5], [2, 2], name = 'layer1')
layer2 = create_new_conv_layer(layer1, 32, 64, [5, 5], [2, 2], name = 'layer2')Step 5- Hãy để chúng tôi làm phẳng đầu ra sẵn sàng cho giai đoạn đầu ra được kết nối đầy đủ - sau hai lớp của bước 2 gộp lại với kích thước 28 x 28, thành kích thước 14 x 14 hoặc tọa độ tối thiểu 7 x 7 x, y, nhưng với 64 các kênh đầu ra. Để tạo kết nối đầy đủ với lớp "dày đặc", hình dạng mới cần phải là [-1, 7 x 7 x 64]. Chúng ta có thể thiết lập một số trọng số và giá trị thiên vị cho lớp này, sau đó kích hoạt bằng ReLU.
flattened = tf.reshape(layer2, [-1, 7 * 7 * 64])
wd1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1000], stddev = 0.03), name = 'wd1')
bd1 = tf.Variable(tf.truncated_normal([1000], stddev = 0.01), name = 'bd1')
dense_layer1 = tf.matmul(flattened, wd1) + bd1
dense_layer1 = tf.nn.relu(dense_layer1)Step 6 - Một lớp khác với các kích hoạt softmax cụ thể với trình tối ưu hóa được yêu cầu xác định đánh giá độ chính xác, giúp thiết lập toán tử khởi tạo.
wd2 = tf.Variable(tf.truncated_normal([1000, 10], stddev = 0.03), name = 'wd2')
bd2 = tf.Variable(tf.truncated_normal([10], stddev = 0.01), name = 'bd2')
dense_layer2 = tf.matmul(dense_layer1, wd2) + bd2
y_ = tf.nn.softmax(dense_layer2)
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits = dense_layer2, labels = y))
optimiser = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
init_op = tf.global_variables_initializer()Step 7- Chúng ta nên thiết lập các biến ghi. Điều này bổ sung một bản tóm tắt để lưu trữ độ chính xác của dữ liệu.
tf.summary.scalar('accuracy', accuracy)
merged = tf.summary.merge_all()
writer = tf.summary.FileWriter('E:\TensorFlowProject')
with tf.Session() as sess:
sess.run(init_op)
total_batch = int(len(mnist.train.labels) / batch_size)
for epoch in range(epochs):
avg_cost = 0
for i in range(total_batch):
batch_x, batch_y = mnist.train.next_batch(batch_size = batch_size)
_, c = sess.run([optimiser, cross_entropy], feed_dict = {
x:batch_x, y: batch_y})
avg_cost += c / total_batch
test_acc = sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
mnist.test.labels})
summary = sess.run(merged, feed_dict = {x: mnist.test.images, y:
mnist.test.labels})
writer.add_summary(summary, epoch)
print("\nTraining complete!")
writer.add_graph(sess.graph)
print(sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
mnist.test.labels}))
def create_new_conv_layer(
input_data, num_input_channels, num_filters,filter_shape, pool_shape, name):
conv_filt_shape = [
filter_shape[0], filter_shape[1], num_input_channels, num_filters]
weights = tf.Variable(
tf.truncated_normal(conv_filt_shape, stddev = 0.03), name = name+'_W')
bias = tf.Variable(tf.truncated_normal([num_filters]), name = name+'_b')
#Out layer defines the output
out_layer =
tf.nn.conv2d(input_data, weights, [1, 1, 1, 1], padding = 'SAME')
out_layer += bias
out_layer = tf.nn.relu(out_layer)
ksize = [1, pool_shape[0], pool_shape[1], 1]
strides = [1, 2, 2, 1]
out_layer = tf.nn.max_pool(
out_layer, ksize = ksize, strides = strides, padding = 'SAME')
return out_layer
if __name__ == "__main__":
run_cnn()Sau đây là kết quả được tạo bởi đoạn mã trên:
See @{tf.nn.softmax_cross_entropy_with_logits_v2}.
2018-09-19 17:22:58.802268: I
T:\src\github\tensorflow\tensorflow\core\platform\cpu_feature_guard.cc:140]
Your CPU supports instructions that this TensorFlow binary was not compiled to
use: AVX2
2018-09-19 17:25:41.522845: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.
2018-09-19 17:25:44.630941: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 501760000 exceeds 10% of system memory.
Epoch: 1 cost = 0.676 test accuracy: 0.940
2018-09-19 17:26:51.987554: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.Mạng nơ-ron tuần hoàn là một loại thuật toán hướng đến học sâu, theo cách tiếp cận tuần tự. Trong mạng nơ-ron, chúng ta luôn giả định rằng mỗi đầu vào và đầu ra là độc lập với tất cả các lớp khác. Loại mạng nơ-ron này được gọi là mạng tái phát vì chúng thực hiện các phép tính toán học theo cách tuần tự.
Hãy xem xét các bước sau để đào tạo một mạng nơ-ron tuần hoàn:
Step 1 - Nhập một ví dụ cụ thể từ tập dữ liệu.
Step 2 - Mạng sẽ lấy một ví dụ và tính toán một số phép tính bằng cách sử dụng các biến được khởi tạo ngẫu nhiên.
Step 3 - Một kết quả dự đoán sau đó được tính toán.
Step 4 - Việc so sánh kết quả thực tế được tạo ra với giá trị mong đợi sẽ tạo ra lỗi.
Step 5 - Để theo dõi lỗi, nó được truyền thông qua cùng một đường dẫn nơi các biến cũng được điều chỉnh.
Step 6 - Các bước từ 1 đến 5 được lặp lại cho đến khi chúng ta tin chắc rằng các biến được khai báo để lấy đầu ra được định nghĩa đúng.
Step 7 - Một dự đoán có hệ thống được thực hiện bằng cách áp dụng các biến này để có được đầu vào mới chưa từng thấy.
Cách tiếp cận giản đồ của việc biểu diễn các mạng nơ-ron lặp lại được mô tả dưới đây:
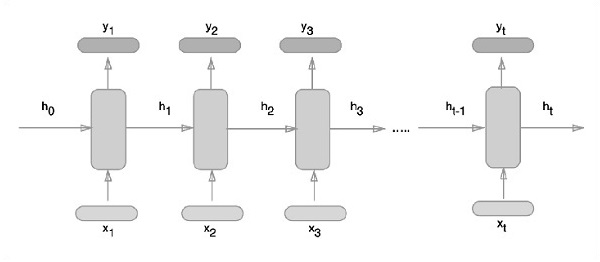
Triển khai mạng thần kinh định kỳ với TensorFlow
Trong phần này, chúng ta sẽ học cách triển khai mạng nơ-ron tuần hoàn với TensorFlow.
Step 1 - TensorFlow bao gồm các thư viện khác nhau để triển khai cụ thể mô-đun mạng nơ-ron tuần hoàn.
#Import necessary modules
from __future__ import print_function
import tensorflow as tf
from tensorflow.contrib import rnn
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)Như đã đề cập ở trên, các thư viện giúp xác định dữ liệu đầu vào, dữ liệu này tạo thành phần chính của việc triển khai mạng nơ-ron tuần hoàn.
Step 2- Động cơ chính của chúng tôi là phân loại hình ảnh bằng cách sử dụng mạng nơ-ron tuần hoàn, nơi chúng tôi coi mỗi hàng hình ảnh là một chuỗi pixel. Hình dạng hình ảnh MNIST được xác định cụ thể là 28 * 28 px. Bây giờ chúng ta sẽ xử lý 28 chuỗi gồm 28 bước cho mỗi mẫu được đề cập. Chúng tôi sẽ xác định các tham số đầu vào để hoàn thành mẫu tuần tự.
n_input = 28 # MNIST data input with img shape 28*28
n_steps = 28
n_hidden = 128
n_classes = 10
# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes]
weights = {
'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
'out': tf.Variable(tf.random_normal([n_classes]))
}Step 3- Tính toán kết quả bằng một hàm xác định trong RNN để có kết quả tốt nhất. Tại đây, mỗi hình dạng dữ liệu được so sánh với hình dạng đầu vào hiện tại và kết quả được tính toán để duy trì tỷ lệ chính xác.
def RNN(x, weights, biases):
x = tf.unstack(x, n_steps, 1)
# Define a lstm cell with tensorflow
lstm_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)
# Get lstm cell output
outputs, states = rnn.static_rnn(lstm_cell, x, dtype = tf.float32)
# Linear activation, using rnn inner loop last output
return tf.matmul(outputs[-1], weights['out']) + biases['out']
pred = RNN(x, weights, biases)
# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = pred, labels = y))
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)
# Evaluate model
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# Initializing the variables
init = tf.global_variables_initializer()Step 4- Ở bước này, chúng ta sẽ khởi chạy đồ thị để lấy kết quả tính toán. Điều này cũng giúp tính toán độ chính xác cho kết quả thử nghiệm.
with tf.Session() as sess:
sess.run(init)
step = 1
# Keep training until reach max iterations
while step * batch_size < training_iters:
batch_x, batch_y = mnist.train.next_batch(batch_size)
batch_x = batch_x.reshape((batch_size, n_steps, n_input))
sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
if step % display_step == 0:
# Calculate batch accuracy
acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
# Calculate batch loss
loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
print("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
step += 1
print("Optimization Finished!")
test_len = 128
test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
test_label = mnist.test.labels[:test_len]
print("Testing Accuracy:", \
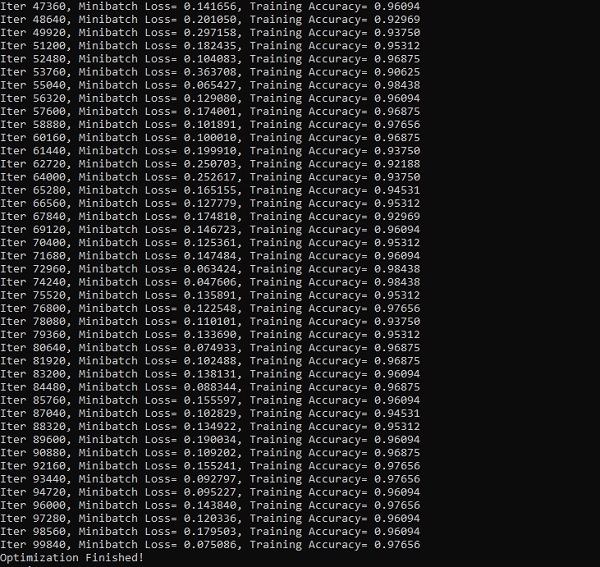
sess.run(accuracy, feed_dict={x: test_data, y: test_label}))Ảnh chụp màn hình bên dưới cho thấy kết quả được tạo -
TensorFlow bao gồm một công cụ trực quan hóa, được gọi là TensorBoard. Nó được sử dụng để phân tích Đồ thị luồng dữ liệu và cũng được sử dụng để hiểu các mô hình học máy. Tính năng quan trọng của TensorBoard bao gồm chế độ xem các loại thống kê khác nhau về các tham số và chi tiết của bất kỳ biểu đồ nào trong căn chỉnh dọc.
Mạng nơron sâu bao gồm lên đến 36.000 nút. TensorBoard giúp thu gọn các nút này trong các khối cấp cao và làm nổi bật các cấu trúc giống hệt nhau. Điều này cho phép phân tích tốt hơn biểu đồ tập trung vào các phần chính của biểu đồ tính toán. Hình ảnh TensorBoard được cho là rất tương tác, nơi người dùng có thể xoay, thu phóng và mở rộng các nút để hiển thị các chi tiết.
Biểu đồ sơ đồ sau cho thấy hoạt động hoàn chỉnh của trực quan hóa TensorBoard -
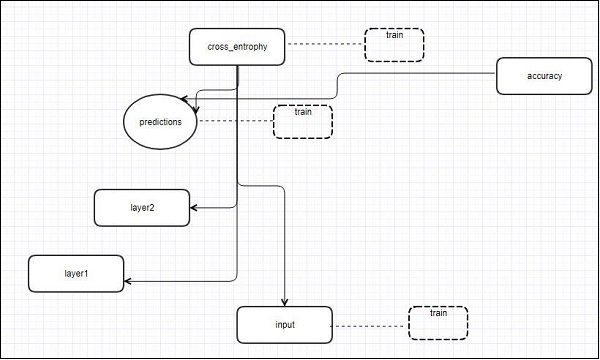
Các thuật toán thu gọn các nút thành các khối cấp cao và làm nổi bật các nhóm cụ thể có cấu trúc giống hệt nhau, phân tách các nút cấp cao. Do đó, TensorBoard được tạo ra rất hữu ích và được coi là quan trọng như nhau để điều chỉnh mô hình học máy. Công cụ trực quan hóa này được thiết kế cho tệp nhật ký cấu hình với thông tin tóm tắt và chi tiết cần được hiển thị.
Chúng ta hãy tập trung vào ví dụ demo của trực quan hóa TensorBoard với sự trợ giúp của đoạn mã sau:
import tensorflow as tf
# Constants creation for TensorBoard visualization
a = tf.constant(10,name = "a")
b = tf.constant(90,name = "b")
y = tf.Variable(a+b*2,name = 'y')
model = tf.initialize_all_variables() #Creation of model
with tf.Session() as session:
merged = tf.merge_all_summaries()
writer = tf.train.SummaryWriter("/tmp/tensorflowlogs",session.graph)
session.run(model)
print(session.run(y))Bảng sau đây cho thấy các ký hiệu khác nhau của trực quan hóa TensorBoard được sử dụng để biểu diễn nút:

Nhúng từ là khái niệm ánh xạ từ các đối tượng rời rạc như từ sang vectơ và số thực. Điều quan trọng là đầu vào cho học máy. Khái niệm này bao gồm các hàm tiêu chuẩn, biến đổi hiệu quả các đối tượng đầu vào rời rạc thành các vectơ hữu ích.
Hình minh họa mẫu về đầu vào của nhúng từ như hình dưới đây -
blue: (0.01359, 0.00075997, 0.24608, ..., -0.2524, 1.0048, 0.06259)
blues: (0.01396, 0.11887, -0.48963, ..., 0.033483, -0.10007, 0.1158)
orange: (-0.24776, -0.12359, 0.20986, ..., 0.079717, 0.23865, -0.014213)
oranges: (-0.35609, 0.21854, 0.080944, ..., -0.35413, 0.38511, -0.070976)Word2vec
Word2vec là cách tiếp cận phổ biến nhất được sử dụng cho kỹ thuật nhúng từ không có giám sát. Nó đào tạo mô hình theo cách mà một từ đầu vào nhất định dự đoán ngữ cảnh của từ đó bằng cách sử dụng bỏ qua gam.
TensorFlow cho phép nhiều cách để triển khai loại mô hình này với mức độ tinh vi và tối ưu hóa ngày càng tăng, đồng thời sử dụng các khái niệm đa luồng và trừu tượng cấp cao hơn.
import os
import math
import numpy as np
import tensorflow as tf
from tensorflow.contrib.tensorboard.plugins import projector
batch_size = 64
embedding_dimension = 5
negative_samples = 8
LOG_DIR = "logs/word2vec_intro"
digit_to_word_map = {
1: "One",
2: "Two",
3: "Three",
4: "Four",
5: "Five",
6: "Six",
7: "Seven",
8: "Eight",
9: "Nine"}
sentences = []
# Create two kinds of sentences - sequences of odd and even digits.
for i in range(10000):
rand_odd_ints = np.random.choice(range(1, 10, 2), 3)
sentences.append(" ".join([digit_to_word_map[r] for r in rand_odd_ints]))
rand_even_ints = np.random.choice(range(2, 10, 2), 3)
sentences.append(" ".join([digit_to_word_map[r] for r in rand_even_ints]))
# Map words to indices
word2index_map = {}
index = 0
for sent in sentences:
for word in sent.lower().split():
if word not in word2index_map:
word2index_map[word] = index
index += 1
index2word_map = {index: word for word, index in word2index_map.items()}
vocabulary_size = len(index2word_map)
# Generate skip-gram pairs
skip_gram_pairs = []
for sent in sentences:
tokenized_sent = sent.lower().split()
for i in range(1, len(tokenized_sent)-1):
word_context_pair = [[word2index_map[tokenized_sent[i-1]],
word2index_map[tokenized_sent[i+1]]], word2index_map[tokenized_sent[i]]]
skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][0]])
skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][1]])
def get_skipgram_batch(batch_size):
instance_indices = list(range(len(skip_gram_pairs)))
np.random.shuffle(instance_indices)
batch = instance_indices[:batch_size]
x = [skip_gram_pairs[i][0] for i in batch]
y = [[skip_gram_pairs[i][1]] for i in batch]
return x, y
# batch example
x_batch, y_batch = get_skipgram_batch(8)
x_batch
y_batch
[index2word_map[word] for word in x_batch] [index2word_map[word[0]] for word in y_batch]
# Input data, labels train_inputs = tf.placeholder(tf.int32, shape = [batch_size])
train_labels = tf.placeholder(tf.int32, shape = [batch_size, 1])
# Embedding lookup table currently only implemented in CPU with
tf.name_scope("embeddings"):
embeddings = tf.Variable(
tf.random_uniform([vocabulary_size, embedding_dimension], -1.0, 1.0),
name = 'embedding')
# This is essentialy a lookup table
embed = tf.nn.embedding_lookup(embeddings, train_inputs)
# Create variables for the NCE loss
nce_weights = tf.Variable(
tf.truncated_normal([vocabulary_size, embedding_dimension], stddev = 1.0 /
math.sqrt(embedding_dimension)))
nce_biases = tf.Variable(tf.zeros([vocabulary_size]))
loss = tf.reduce_mean(
tf.nn.nce_loss(weights = nce_weights, biases = nce_biases, inputs = embed,
labels = train_labels,num_sampled = negative_samples,
num_classes = vocabulary_size)) tf.summary.scalar("NCE_loss", loss)
# Learning rate decay
global_step = tf.Variable(0, trainable = False)
learningRate = tf.train.exponential_decay(learning_rate = 0.1,
global_step = global_step, decay_steps = 1000, decay_rate = 0.95, staircase = True)
train_step = tf.train.GradientDescentOptimizer(learningRate).minimize(loss)
merged = tf.summary.merge_all()
with tf.Session() as sess:
train_writer = tf.summary.FileWriter(LOG_DIR,
graph = tf.get_default_graph())
saver = tf.train.Saver()
with open(os.path.join(LOG_DIR, 'metadata.tsv'), "w") as metadata:
metadata.write('Name\tClass\n') for k, v in index2word_map.items():
metadata.write('%s\t%d\n' % (v, k))
config = projector.ProjectorConfig()
embedding = config.embeddings.add() embedding.tensor_name = embeddings.name
# Link this tensor to its metadata file (e.g. labels).
embedding.metadata_path = os.path.join(LOG_DIR, 'metadata.tsv')
projector.visualize_embeddings(train_writer, config)
tf.global_variables_initializer().run()
for step in range(1000):
x_batch, y_batch = get_skipgram_batch(batch_size) summary, _ = sess.run(
[merged, train_step], feed_dict = {train_inputs: x_batch, train_labels: y_batch})
train_writer.add_summary(summary, step)
if step % 100 == 0:
saver.save(sess, os.path.join(LOG_DIR, "w2v_model.ckpt"), step)
loss_value = sess.run(loss, feed_dict = {
train_inputs: x_batch, train_labels: y_batch})
print("Loss at %d: %.5f" % (step, loss_value))
# Normalize embeddings before using
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims = True))
normalized_embeddings = embeddings /
norm normalized_embeddings_matrix = sess.run(normalized_embeddings)
ref_word = normalized_embeddings_matrix[word2index_map["one"]]
cosine_dists = np.dot(normalized_embeddings_matrix, ref_word)
ff = np.argsort(cosine_dists)[::-1][1:10] for f in ff: print(index2word_map[f])
print(cosine_dists[f])Đầu ra
Đoạn mã trên tạo ra kết quả sau:
Để hiểu được perceptron lớp đơn, điều quan trọng là phải hiểu Mạng thần kinh nhân tạo (ANN). Mạng nơron nhân tạo là hệ thống xử lý thông tin mà cơ chế của nó được lấy cảm hứng từ các chức năng của các mạch thần kinh sinh học. Một mạng nơ-ron nhân tạo sở hữu nhiều đơn vị xử lý được kết nối với nhau. Sau đây là biểu diễn giản đồ của mạng nơron nhân tạo:
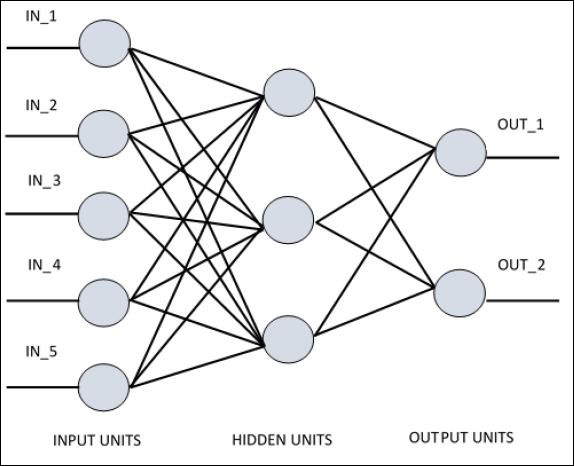
Biểu đồ cho thấy rằng các đơn vị ẩn giao tiếp với lớp bên ngoài. Trong khi các đơn vị đầu vào và đầu ra chỉ giao tiếp thông qua lớp ẩn của mạng.
Mô hình kết nối với các nút, tổng số lớp và mức độ của các nút giữa đầu vào và đầu ra với số lượng tế bào thần kinh trên mỗi lớp xác định kiến trúc của mạng thần kinh.
Có hai kiểu kiến trúc. Các loại này tập trung vào các mạng nơron nhân tạo có chức năng như sau:
- Perceptron một lớp
- Perceptron nhiều lớp
Perceptron một lớp
Perceptron lớp đơn là mô hình thần kinh được đề xuất đầu tiên được tạo ra. Nội dung của bộ nhớ cục bộ của nơ-ron bao gồm một vectơ trọng số. Việc tính toán một perceptron lớp đơn được thực hiện dựa trên phép tính tổng của từng vectơ đầu vào với giá trị nhân với phần tử tương ứng của vectơ của trọng số. Giá trị được hiển thị trong đầu ra sẽ là đầu vào của một chức năng kích hoạt.

Chúng ta hãy tập trung vào việc triển khai perceptron lớp đơn cho vấn đề phân loại ảnh bằng TensorFlow. Ví dụ tốt nhất để minh họa perceptron lớp đơn là thông qua biểu diễn "Hồi quy logistic".
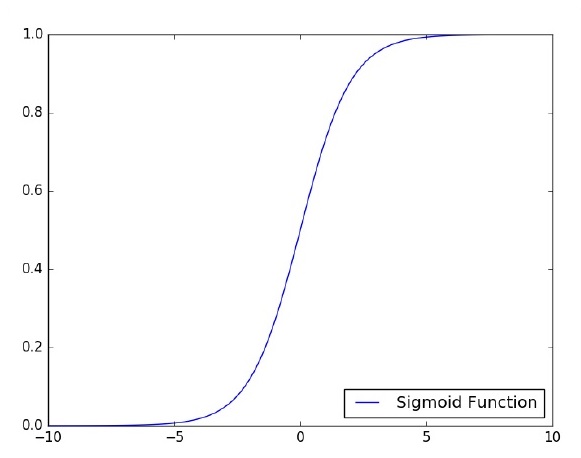
Bây giờ, chúng ta hãy xem xét các bước cơ bản sau đây của đào tạo hồi quy logistic -
Các trọng số được khởi tạo với các giá trị ngẫu nhiên khi bắt đầu huấn luyện.
Đối với mỗi phần tử của tập huấn luyện, sai số được tính toán với sự khác biệt giữa đầu ra mong muốn và đầu ra thực tế. Sai số được tính toán được sử dụng để điều chỉnh trọng số.
Quá trình được lặp lại cho đến khi lỗi thực hiện trên toàn bộ tập huấn luyện không nhỏ hơn ngưỡng đã chỉ định, cho đến khi đạt được số lần lặp tối đa.
Mã hoàn chỉnh để đánh giá hồi quy logistic được đề cập dưới đây:
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.01
training_epochs = 25
batch_size = 100
display_step = 1
# tf Graph Input
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes
# Create model
# Set model weights
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# Construct model
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax
# Minimize error using cross entropy
cross_entropy = y*tf.log(activation)
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1))
optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost)
#Plot settings
avg_set = []
epoch_set = []
# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
# Training cycle
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
# Fit training using batch data sess.run(optimizer, \ feed_dict = {
x: batch_xs, y: batch_ys})
# Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
x: batch_xs, \ y: batch_ys})/total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
avg_set.append(avg_cost) epoch_set.append(epoch+1)
print ("Training phase finished")
plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test model
correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1))
# Calculate accuracy
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print
("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))Đầu ra
Đoạn mã trên tạo ra kết quả sau:
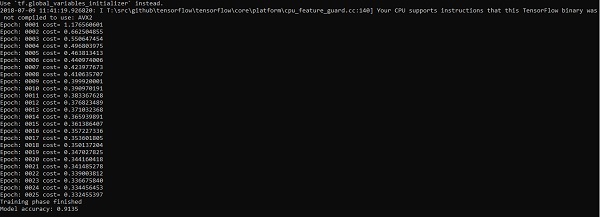
Hồi quy logistic được coi là một phân tích dự báo. Hồi quy logistic được sử dụng để mô tả dữ liệu và giải thích mối quan hệ giữa một biến nhị phân phụ thuộc và một hoặc nhiều biến danh nghĩa hoặc độc lập.
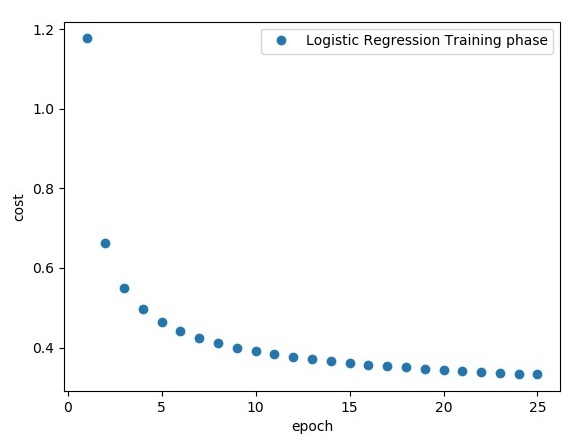
Trong chương này, chúng ta sẽ tập trung vào ví dụ cơ bản về triển khai hồi quy tuyến tính bằng TensorFlow. Hồi quy logistic hoặc hồi quy tuyến tính là một cách tiếp cận máy học có giám sát để phân loại các danh mục rời rạc theo thứ tự. Mục tiêu của chúng tôi trong chương này là xây dựng một mô hình mà qua đó người dùng có thể dự đoán mối quan hệ giữa các biến dự báo và một hoặc nhiều biến độc lập.
Mối quan hệ giữa hai biến này được coi là tuyến tính. Nếu y là biến phụ thuộc và x được coi là biến độc lập, thì mối quan hệ hồi quy tuyến tính của hai biến sẽ giống như phương trình sau:
Y = Ax+bChúng tôi sẽ thiết kế một thuật toán cho hồi quy tuyến tính. Điều này sẽ cho phép chúng ta hiểu hai khái niệm quan trọng sau:
- Chức năng ước lượng
- Các thuật toán giảm dần độ dốc
Biểu diễn giản đồ của hồi quy tuyến tính được đề cập dưới đây:

Hình ảnh đồ thị của phương trình hồi quy tuyến tính được đề cập dưới đây:
Các bước thiết kế một thuật toán cho hồi quy tuyến tính
Bây giờ chúng ta sẽ tìm hiểu về các bước giúp thiết kế một thuật toán cho hồi quy tuyến tính.
Bước 1
Điều quan trọng là nhập các mô-đun cần thiết để vẽ mô-đun hồi quy tuyến tính. Chúng tôi bắt đầu nhập thư viện Python NumPy và Matplotlib.
import numpy as np
import matplotlib.pyplot as pltBước 2
Xác định số lượng hệ số cần thiết cho hồi quy logistic.
number_of_points = 500
x_point = []
y_point = []
a = 0.22
b = 0.78Bước 3
Lặp lại các biến để tạo ra 300 điểm ngẫu nhiên xung quanh phương trình hồi quy -
Y = 0,22x + 0,78
for i in range(number_of_points):
x = np.random.normal(0.0,0.5)
y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x])
y_point.append([y])Bước 4
Xem các điểm được tạo bằng Matplotlib.
fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()Mã hoàn chỉnh cho hồi quy logistic như sau:
import numpy as np
import matplotlib.pyplot as plt
number_of_points = 500
x_point = []
y_point = []
a = 0.22
b = 0.78
for i in range(number_of_points):
x = np.random.normal(0.0,0.5)
y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x])
y_point.append([y])
plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend()
plt.show()Số điểm được lấy làm đầu vào được coi là dữ liệu đầu vào.
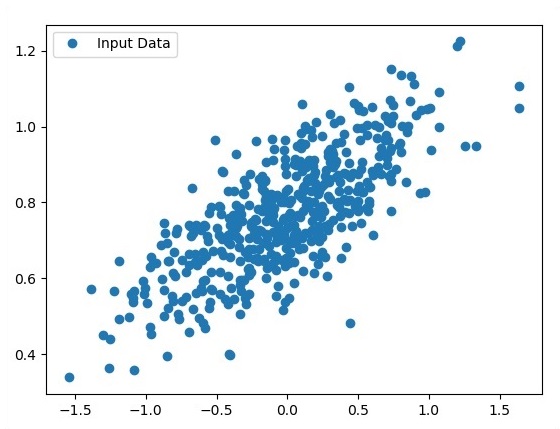
TFLearn có thể được định nghĩa là một khía cạnh học sâu mô-đun và minh bạch được sử dụng trong khuôn khổ TensorFlow. Động cơ chính của TFLearn là cung cấp API cấp cao hơn cho TensorFlow để tạo điều kiện và hiển thị các thử nghiệm mới.
Hãy xem xét các tính năng quan trọng sau của TFLearn:
TFLearn rất dễ sử dụng và dễ hiểu.
Nó bao gồm các khái niệm dễ dàng để xây dựng các lớp mạng mô-đun cao, trình tối ưu hóa và các số liệu khác nhau được nhúng bên trong chúng.
Nó bao gồm sự minh bạch đầy đủ với hệ thống làm việc TensorFlow.
Nó bao gồm các chức năng trợ giúp mạnh mẽ để huấn luyện các bộ căng tích hợp chấp nhận nhiều đầu vào, đầu ra và trình tối ưu hóa.
Nó bao gồm hình ảnh đồ thị dễ dàng và đẹp mắt.
Hình ảnh hóa biểu đồ bao gồm các chi tiết khác nhau về trọng số, độ dốc và kích hoạt.
Cài đặt TFLearn bằng cách thực hiện lệnh sau:
pip install tflearnKhi thực thi đoạn mã trên, kết quả sau sẽ được tạo:
Hình minh họa sau đây cho thấy việc triển khai TFLearn với bộ phân loại Rừng Ngẫu nhiên -
from __future__ import division, print_function, absolute_import
#TFLearn module implementation
import tflearn
from tflearn.estimators import RandomForestClassifier
# Data loading and pre-processing with respect to dataset
import tflearn.datasets.mnist as mnist
X, Y, testX, testY = mnist.load_data(one_hot = False)
m = RandomForestClassifier(n_estimators = 100, max_nodes = 1000)
m.fit(X, Y, batch_size = 10000, display_step = 10)
print("Compute the accuracy on train data:")
print(m.evaluate(X, Y, tflearn.accuracy_op))
print("Compute the accuracy on test set:")
print(m.evaluate(testX, testY, tflearn.accuracy_op))
print("Digits for test images id 0 to 5:")
print(m.predict(testX[:5]))
print("True digits:")
print(testY[:5])Trong chương này, chúng tôi sẽ tập trung vào sự khác biệt giữa CNN và RNN -
| CNN | RNN |
|---|---|
| Nó phù hợp với dữ liệu không gian như hình ảnh. | RNN phù hợp với dữ liệu tạm thời, còn được gọi là dữ liệu tuần tự. |
| CNN được coi là mạnh hơn RNN. | RNN bao gồm ít tính năng tương thích hơn khi so sánh với CNN. |
| Mạng này nhận các đầu vào có kích thước cố định và tạo ra các đầu ra có kích thước cố định. | RNN có thể xử lý độ dài đầu vào / đầu ra tùy ý. |
| CNN là một loại mạng nơ-ron nhân tạo chuyển tiếp với các biến thể của các perceptron nhiều lớp được thiết kế để sử dụng lượng tiền xử lý tối thiểu. | RNN không giống như các mạng nơ-ron chuyển tiếp nguồn cấp dữ liệu - có thể sử dụng bộ nhớ trong của chúng để xử lý các chuỗi đầu vào tùy ý. |
| CNN sử dụng mô hình kết nối giữa các nơ-ron. Điều này được lấy cảm hứng từ tổ chức của vỏ não động vật, có các tế bào thần kinh riêng lẻ được sắp xếp theo cách mà chúng phản ứng với các vùng chồng chéo lên nhau trong trường thị giác. | Các mạng nơ-ron lặp lại sử dụng thông tin chuỗi thời gian - những gì người dùng nói lần cuối sẽ ảnh hưởng đến những gì họ sẽ nói tiếp theo. |
| CNN rất lý tưởng để xử lý hình ảnh và video. | RNN rất lý tưởng để phân tích văn bản và giọng nói. |
Hình minh họa sau đây cho thấy biểu diễn giản đồ của CNN và RNN -
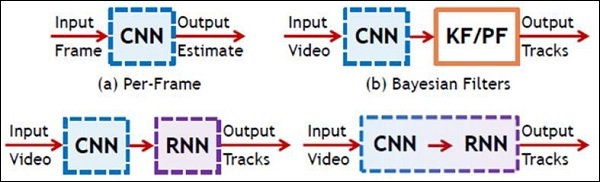
Keras nhỏ gọn, dễ học, thư viện Python cấp cao chạy trên khung công tác TensorFlow. Nó được thực hiện tập trung vào việc hiểu các kỹ thuật học sâu, chẳng hạn như tạo các lớp cho mạng nơ-ron duy trì các khái niệm về hình dạng và chi tiết toán học. Việc tạo tác phẩm tự do có thể thuộc hai loại sau:
- API tuần tự
- API chức năng
Hãy xem xét tám bước sau để tạo mô hình học sâu trong Keras:
- Đang tải dữ liệu
- Xử lý trước dữ liệu đã tải
- Định nghĩa mô hình
- Biên dịch mô hình
- Phù hợp với mô hình được chỉ định
- Đánh giá nó
- Đưa ra các dự đoán bắt buộc
- Lưu mô hình
Chúng tôi sẽ sử dụng Máy tính xách tay Jupyter để thực thi và hiển thị đầu ra như hình dưới đây -
Step 1 - Việc tải dữ liệu và xử lý trước dữ liệu đã tải được thực hiện đầu tiên để thực thi mô hình học sâu.
import warnings
warnings.filterwarnings('ignore')
import numpy as np
np.random.seed(123) # for reproducibility
from keras.models import Sequential
from keras.layers import Flatten, MaxPool2D, Conv2D, Dense, Reshape, Dropout
from keras.utils import np_utils
Using TensorFlow backend.
from keras.datasets import mnist
# Load pre-shuffled MNIST data into train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Y_train = np_utils.to_categorical(y_train, 10)
Y_test = np_utils.to_categorical(y_test, 10)Bước này có thể được định nghĩa là “Nhập thư viện và mô-đun” có nghĩa là tất cả các thư viện và mô-đun được nhập như một bước ban đầu.
Step 2 - Trong bước này, chúng ta sẽ xác định kiến trúc mô hình -
model = Sequential()
model.add(Conv2D(32, 3, 3, activation = 'relu', input_shape = (28,28,1)))
model.add(Conv2D(32, 3, 3, activation = 'relu'))
model.add(MaxPool2D(pool_size = (2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation = 'relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation = 'softmax'))Step 3 - Bây giờ chúng ta hãy biên dịch mô hình được chỉ định -
model.compile(loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['accuracy'])Step 4 - Bây giờ chúng tôi sẽ phù hợp với mô hình bằng cách sử dụng dữ liệu đào tạo -
model.fit(X_train, Y_train, batch_size = 32, epochs = 10, verbose = 1)Đầu ra của các lần lặp được tạo như sau:
Epoch 1/10 60000/60000 [==============================] - 65s -
loss: 0.2124 -
acc: 0.9345
Epoch 2/10 60000/60000 [==============================] - 62s -
loss: 0.0893 -
acc: 0.9740
Epoch 3/10 60000/60000 [==============================] - 58s -
loss: 0.0665 -
acc: 0.9802
Epoch 4/10 60000/60000 [==============================] - 62s -
loss: 0.0571 -
acc: 0.9830
Epoch 5/10 60000/60000 [==============================] - 62s -
loss: 0.0474 -
acc: 0.9855
Epoch 6/10 60000/60000 [==============================] - 59s -
loss: 0.0416 -
acc: 0.9871
Epoch 7/10 60000/60000 [==============================] - 61s -
loss: 0.0380 -
acc: 0.9877
Epoch 8/10 60000/60000 [==============================] - 63s -
loss: 0.0333 -
acc: 0.9895
Epoch 9/10 60000/60000 [==============================] - 64s -
loss: 0.0325 -
acc: 0.9898
Epoch 10/10 60000/60000 [==============================] - 60s -
loss: 0.0284 -
acc: 0.9910Chương này sẽ tập trung vào cách bắt đầu với TensorFlow phân tán. Mục đích là giúp các nhà phát triển hiểu các khái niệm TF phân tán cơ bản đang tái diễn, chẳng hạn như máy chủ TF. Chúng tôi sẽ sử dụng Jupyter Notebook để đánh giá TensorFlow phân tán. Việc triển khai tính toán phân tán với TensorFlow được đề cập dưới đây:
Step 1 - Nhập các mô-đun cần thiết bắt buộc cho tính toán phân tán -
import tensorflow as tfStep 2- Tạo một cụm TensorFlow với một nút. Hãy để nút này chịu trách nhiệm cho một công việc có tên "worker" và nó sẽ hoạt động một lần tại localhost: 2222.
cluster_spec = tf.train.ClusterSpec({'worker' : ['localhost:2222']})
server = tf.train.Server(cluster_spec)
server.targetCác đoạn mã trên tạo ra kết quả sau:
'grpc://localhost:2222'
The server is currently running.Step 3 - Cấu hình máy chủ với phiên tương ứng có thể được tính toán bằng cách thực hiện lệnh sau:
server.server_defLệnh trên tạo ra kết quả sau:
cluster {
job {
name: "worker"
tasks {
value: "localhost:2222"
}
}
}
job_name: "worker"
protocol: "grpc"Step 4- Khởi chạy một phiên TensorFlow với công cụ thực thi là máy chủ. Sử dụng TensorFlow để tạo máy chủ cục bộ và sử dụnglsof để tìm ra vị trí của máy chủ.
sess = tf.Session(target = server.target)
server = tf.train.Server.create_local_server()Step 5 - Xem các thiết bị có sẵn trong phiên này và đóng phiên tương ứng.
devices = sess.list_devices()
for d in devices:
print(d.name)
sess.close()Lệnh trên tạo ra kết quả sau:
/job:worker/replica:0/task:0/device:CPU:0Ở đây, chúng ta sẽ tập trung vào việc hình thành MetaGraph trong TensorFlow. Điều này sẽ giúp chúng tôi hiểu mô-đun xuất trong TensorFlow. MetaGraph chứa thông tin cơ bản, được yêu cầu để đào tạo, thực hiện đánh giá hoặc chạy suy luận trên một biểu đồ đã được đào tạo trước đó.
Sau đây là đoạn mã cho cùng một -
def export_meta_graph(filename = None, collection_list = None, as_text = False):
"""this code writes `MetaGraphDef` to save_path/filename.
Arguments:
filename: Optional meta_graph filename including the path. collection_list:
List of string keys to collect. as_text: If `True`,
writes the meta_graph as an ASCII proto.
Returns:
A `MetaGraphDef` proto. """Một trong những mô hình sử dụng điển hình cho điều tương tự được đề cập dưới đây:
# Build the model ...
with tf.Session() as sess:
# Use the model ...
# Export the model to /tmp/my-model.meta.
meta_graph_def = tf.train.export_meta_graph(filename = '/tmp/my-model.meta')Multi-Layer perceptron định nghĩa kiến trúc phức tạp nhất của mạng nơ-ron nhân tạo. Về cơ bản, nó được hình thành từ nhiều lớp perceptron.
Biểu diễn sơ đồ của việc học perceptron nhiều lớp như hình dưới đây:
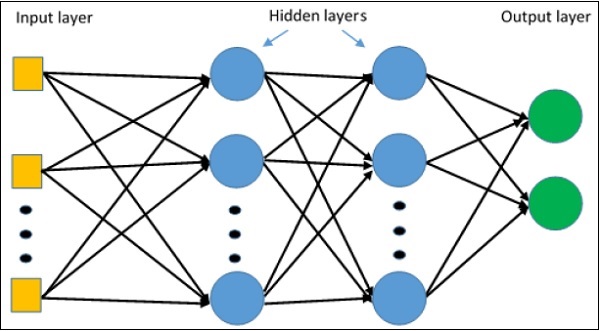
Mạng MLP thường được sử dụng cho định dạng học có giám sát. Một thuật toán học điển hình cho mạng MLP còn được gọi là thuật toán lan truyền ngược.
Bây giờ, chúng ta sẽ tập trung vào việc triển khai với MLP cho một bài toán phân loại hình ảnh.
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.001
training_epochs = 20
batch_size = 100
display_step = 1
# Network Parameters
n_hidden_1 = 256
# 1st layer num features
n_hidden_2 = 256 # 2nd layer num features
n_input = 784 # MNIST data input (img shape: 28*28) n_classes = 10
# MNIST total classes (0-9 digits)
# tf Graph input
x = tf.placeholder("float", [None, n_input])
y = tf.placeholder("float", [None, n_classes])
# weights layer 1
h = tf.Variable(tf.random_normal([n_input, n_hidden_1])) # bias layer 1
bias_layer_1 = tf.Variable(tf.random_normal([n_hidden_1]))
# layer 1 layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, h), bias_layer_1))
# weights layer 2
w = tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2]))
# bias layer 2
bias_layer_2 = tf.Variable(tf.random_normal([n_hidden_2]))
# layer 2
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w), bias_layer_2))
# weights output layer
output = tf.Variable(tf.random_normal([n_hidden_2, n_classes]))
# biar output layer
bias_output = tf.Variable(tf.random_normal([n_classes])) # output layer
output_layer = tf.matmul(layer_2, output) + bias_output
# cost function
cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
logits = output_layer, labels = y))
#cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(output_layer, y))
# optimizer
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)
# optimizer = tf.train.GradientDescentOptimizer(
learning_rate = learning_rate).minimize(cost)
# Plot settings
avg_set = []
epoch_set = []
# Initializing the variables
init = tf.global_variables_initializer()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
# Training cycle
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples / batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# Fit training using batch data sess.run(optimizer, feed_dict = {
x: batch_xs, y: batch_ys})
# Compute average loss
avg_cost += sess.run(cost, feed_dict = {x: batch_xs, y: batch_ys}) / total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print
Epoch:", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(avg_cost)
avg_set.append(avg_cost)
epoch_set.append(epoch + 1)
print
"Training phase finished"
plt.plot(epoch_set, avg_set, 'o', label = 'MLP Training phase')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test model
correct_prediction = tf.equal(tf.argmax(output_layer, 1), tf.argmax(y, 1))
# Calculate accuracy
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print
"Model Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels})Dòng mã trên tạo ra kết quả sau:
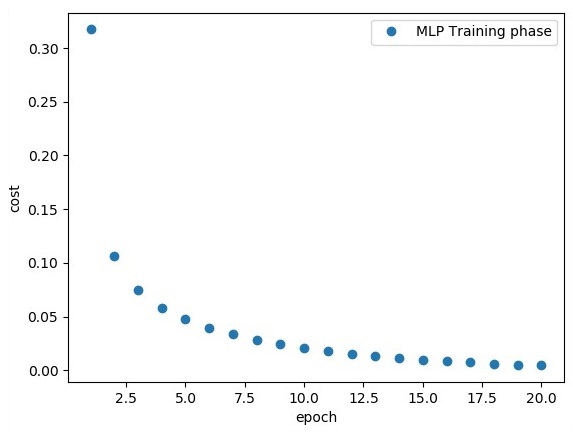
Trong chương này, chúng ta sẽ tập trung vào mạng mà chúng ta sẽ phải học từ tập hợp các điểm đã biết được gọi là x và f (x). Một lớp ẩn duy nhất sẽ xây dựng mạng đơn giản này.
Mã giải thích về các lớp ẩn của perceptron như hình dưới đây:
#Importing the necessary modules
import tensorflow as tf
import numpy as np
import math, random
import matplotlib.pyplot as plt
np.random.seed(1000)
function_to_learn = lambda x: np.cos(x) + 0.1*np.random.randn(*x.shape)
layer_1_neurons = 10
NUM_points = 1000
#Training the parameters
batch_size = 100
NUM_EPOCHS = 1500
all_x = np.float32(np.random.uniform(-2*math.pi, 2*math.pi, (1, NUM_points))).T
np.random.shuffle(all_x)
train_size = int(900)
#Training the first 700 points in the given set x_training = all_x[:train_size]
y_training = function_to_learn(x_training)
#Training the last 300 points in the given set x_validation = all_x[train_size:]
y_validation = function_to_learn(x_validation)
plt.figure(1)
plt.scatter(x_training, y_training, c = 'blue', label = 'train')
plt.scatter(x_validation, y_validation, c = 'pink', label = 'validation')
plt.legend()
plt.show()
X = tf.placeholder(tf.float32, [None, 1], name = "X")
Y = tf.placeholder(tf.float32, [None, 1], name = "Y")
#first layer
#Number of neurons = 10
w_h = tf.Variable(
tf.random_uniform([1, layer_1_neurons],\ minval = -1, maxval = 1, dtype = tf.float32))
b_h = tf.Variable(tf.zeros([1, layer_1_neurons], dtype = tf.float32))
h = tf.nn.sigmoid(tf.matmul(X, w_h) + b_h)
#output layer
#Number of neurons = 10
w_o = tf.Variable(
tf.random_uniform([layer_1_neurons, 1],\ minval = -1, maxval = 1, dtype = tf.float32))
b_o = tf.Variable(tf.zeros([1, 1], dtype = tf.float32))
#build the model
model = tf.matmul(h, w_o) + b_o
#minimize the cost function (model - Y)
train_op = tf.train.AdamOptimizer().minimize(tf.nn.l2_loss(model - Y))
#Start the Learning phase
sess = tf.Session() sess.run(tf.initialize_all_variables())
errors = []
for i in range(NUM_EPOCHS):
for start, end in zip(range(0, len(x_training), batch_size),\
range(batch_size, len(x_training), batch_size)):
sess.run(train_op, feed_dict = {X: x_training[start:end],\ Y: y_training[start:end]})
cost = sess.run(tf.nn.l2_loss(model - y_validation),\ feed_dict = {X:x_validation})
errors.append(cost)
if i%100 == 0:
print("epoch %d, cost = %g" % (i, cost))
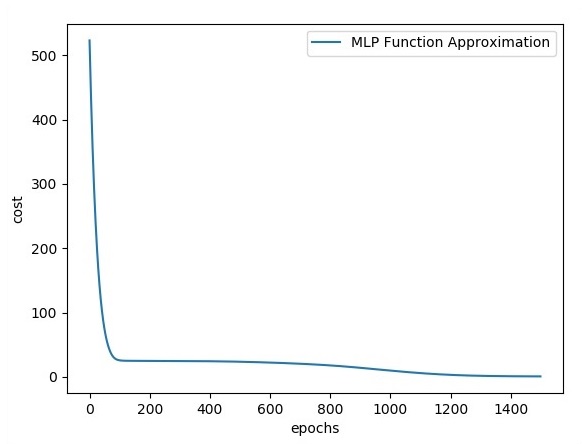
plt.plot(errors,label='MLP Function Approximation') plt.xlabel('epochs')
plt.ylabel('cost')
plt.legend()
plt.show()Đầu ra
Sau đây là biểu diễn của xấp xỉ lớp chức năng:
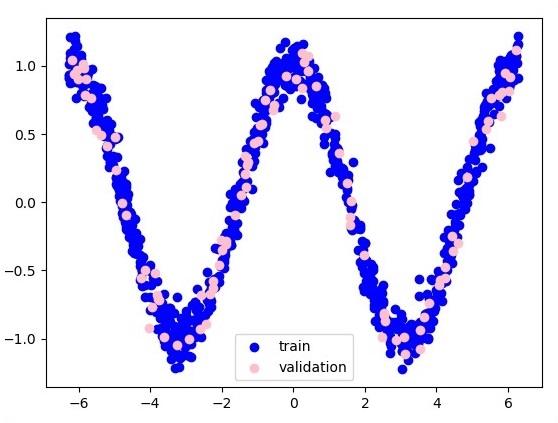
Ở đây hai dữ liệu được biểu diễn dưới dạng chữ W. Hai dữ liệu là: train và validation được thể hiện bằng các màu riêng biệt có thể nhìn thấy trong phần chú giải.
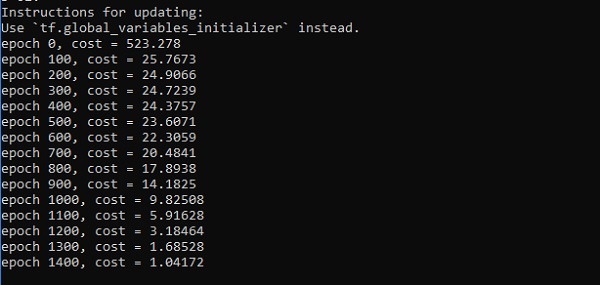
Trình tối ưu hóa là lớp mở rộng, bao gồm thông tin bổ sung để đào tạo một mô hình cụ thể. Lớp tối ưu hóa được khởi tạo với các tham số đã cho nhưng điều quan trọng cần nhớ là không cần Tensor. Bộ tối ưu hóa được sử dụng để cải thiện tốc độ và hiệu suất để đào tạo một mô hình cụ thể.
Trình tối ưu hóa cơ bản của TensorFlow là:
tf.train.OptimizerLớp này được định nghĩa trong đường dẫn cụ thể của tensorflow / python / training / Optimizer.py.
Sau đây là một số trình tối ưu hóa trong Tensorflow -
- Stochastic Gradient descent
- Đổ dốc Stochastic Gradient với cắt gradient
- Momentum
- Động lượng Nesterov
- Adagrad
- Adadelta
- RMSProp
- Adam
- Adamax
- SMORMS3
Chúng tôi sẽ tập trung vào gốc Stochastic Gradient. Hình minh họa để tạo trình tối ưu hóa tương tự được đề cập bên dưới:
def sgd(cost, params, lr = np.float32(0.01)):
g_params = tf.gradients(cost, params)
updates = []
for param, g_param in zip(params, g_params):
updates.append(param.assign(param - lr*g_param))
return updatesCác tham số cơ bản được xác định trong hàm cụ thể. Trong chương tiếp theo của chúng tôi, chúng tôi sẽ tập trung vào Tối ưu hóa Gradient Descent với việc triển khai các trình tối ưu hóa.
Trong chương này, chúng ta sẽ tìm hiểu về việc triển khai XOR bằng TensorFlow. Trước khi bắt đầu triển khai XOR trong TensorFlow, chúng ta hãy xem các giá trị bảng XOR. Điều này sẽ giúp chúng tôi hiểu quá trình mã hóa và giải mã.
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Phương pháp mã hóa XOR Cipher về cơ bản được sử dụng để mã hóa dữ liệu khó bị bẻ khóa bằng phương pháp brute force, tức là bằng cách tạo các khóa mã hóa ngẫu nhiên khớp với khóa thích hợp.
Khái niệm triển khai với XOR Cipher là xác định khóa mã hóa XOR và sau đó thực hiện thao tác XOR của các ký tự trong chuỗi được chỉ định với khóa này mà người dùng cố gắng mã hóa. Bây giờ chúng ta sẽ tập trung vào việc triển khai XOR bằng cách sử dụng TensorFlow, được đề cập bên dưới:
#Declaring necessary modules
import tensorflow as tf
import numpy as np
"""
A simple numpy implementation of a XOR gate to understand the backpropagation
algorithm
"""
x = tf.placeholder(tf.float64,shape = [4,2],name = "x")
#declaring a place holder for input x
y = tf.placeholder(tf.float64,shape = [4,1],name = "y")
#declaring a place holder for desired output y
m = np.shape(x)[0]#number of training examples
n = np.shape(x)[1]#number of features
hidden_s = 2 #number of nodes in the hidden layer
l_r = 1#learning rate initialization
theta1 = tf.cast(tf.Variable(tf.random_normal([3,hidden_s]),name = "theta1"),tf.float64)
theta2 = tf.cast(tf.Variable(tf.random_normal([hidden_s+1,1]),name = "theta2"),tf.float64)
#conducting forward propagation
a1 = tf.concat([np.c_[np.ones(x.shape[0])],x],1)
#the weights of the first layer are multiplied by the input of the first layer
z1 = tf.matmul(a1,theta1)
#the input of the second layer is the output of the first layer, passed through the
activation function and column of biases is added
a2 = tf.concat([np.c_[np.ones(x.shape[0])],tf.sigmoid(z1)],1)
#the input of the second layer is multiplied by the weights
z3 = tf.matmul(a2,theta2)
#the output is passed through the activation function to obtain the final probability
h3 = tf.sigmoid(z3)
cost_func = -tf.reduce_sum(y*tf.log(h3)+(1-y)*tf.log(1-h3),axis = 1)
#built in tensorflow optimizer that conducts gradient descent using specified
learning rate to obtain theta values
optimiser = tf.train.GradientDescentOptimizer(learning_rate = l_r).minimize(cost_func)
#setting required X and Y values to perform XOR operation
X = [[0,0],[0,1],[1,0],[1,1]]
Y = [[0],[1],[1],[0]]
#initializing all variables, creating a session and running a tensorflow session
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
#running gradient descent for each iteration and printing the hypothesis
obtained using the updated theta values
for i in range(100000):
sess.run(optimiser, feed_dict = {x:X,y:Y})#setting place holder values using feed_dict
if i%100==0:
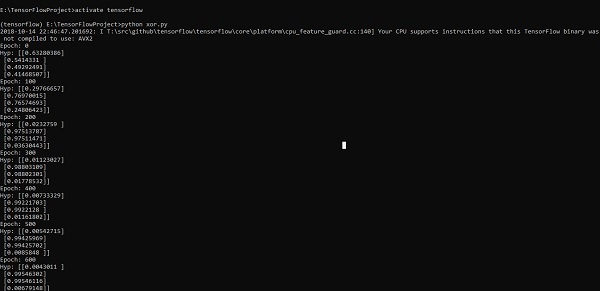
print("Epoch:",i)
print("Hyp:",sess.run(h3,feed_dict = {x:X,y:Y}))Dòng mã trên tạo ra một đầu ra như được hiển thị trong ảnh chụp màn hình bên dưới -
Tối ưu hóa gradient descent được coi là một khái niệm quan trọng trong khoa học dữ liệu.
Hãy xem xét các bước được hiển thị bên dưới để hiểu việc triển khai tối ưu hóa dốc gradient -
Bước 1
Bao gồm các mô-đun cần thiết và khai báo các biến x và y mà qua đó chúng ta sẽ xác định tối ưu hóa gradient descent.
import tensorflow as tf
x = tf.Variable(2, name = 'x', dtype = tf.float32)
log_x = tf.log(x)
log_x_squared = tf.square(log_x)
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(log_x_squared)Bước 2
Khởi tạo các biến cần thiết và gọi trình tối ưu hóa để xác định và gọi nó với chức năng tương ứng.
init = tf.initialize_all_variables()
def optimize():
with tf.Session() as session:
session.run(init)
print("starting at", "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
for step in range(10):
session.run(train)
print("step", step, "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
optimize()Dòng mã trên tạo ra một đầu ra như được hiển thị trong ảnh chụp màn hình bên dưới -
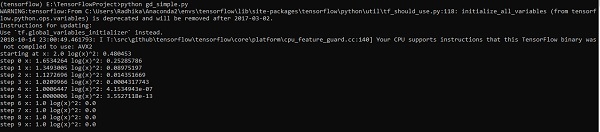
Chúng ta có thể thấy rằng các kỷ nguyên và số lần lặp cần thiết được tính toán như trong đầu ra.
Phương trình vi phân riêng (PDE) là một phương trình vi phân, bao gồm các đạo hàm riêng với hàm chưa biết của một số biến độc lập. Với tham chiếu đến các phương trình đạo hàm riêng, chúng tôi sẽ tập trung vào việc tạo các đồ thị mới.
Giả sử có một cái ao với kích thước 500 * 500 vuông -
N = 500
Bây giờ, chúng ta sẽ tính toán phương trình vi phân riêng và tạo thành đồ thị tương ứng bằng cách sử dụng nó. Hãy xem xét các bước được đưa ra dưới đây cho đồ thị tính toán.
Step 1 - Nhập thư viện để mô phỏng.
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as pltStep 2 - Bao gồm các hàm để biến đổi mảng 2D thành một nhân tích chập và phép toán tích chập 2D đơn giản.
def make_kernel(a):
a = np.asarray(a)
a = a.reshape(list(a.shape) + [1,1])
return tf.constant(a, dtype=1)
def simple_conv(x, k):
"""A simplified 2D convolution operation"""
x = tf.expand_dims(tf.expand_dims(x, 0), -1)
y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding = 'SAME')
return y[0, :, :, 0]
def laplace(x):
"""Compute the 2D laplacian of an array"""
laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]])
return simple_conv(x, laplace_k)
sess = tf.InteractiveSession()Step 3 - Bao gồm số lần lặp và tính toán biểu đồ để hiển thị các bản ghi cho phù hợp.
N = 500
# Initial Conditions -- some rain drops hit a pond
# Set everything to zero
u_init = np.zeros([N, N], dtype = np.float32)
ut_init = np.zeros([N, N], dtype = np.float32)
# Some rain drops hit a pond at random points
for n in range(100):
a,b = np.random.randint(0, N, 2)
u_init[a,b] = np.random.uniform()
plt.imshow(u_init)
plt.show()
# Parameters:
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape = ())
damping = tf.placeholder(tf.float32, shape = ())
# Create variables for simulation state
U = tf.Variable(u_init)
Ut = tf.Variable(ut_init)
# Discretized PDE update rules
U_ = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)
# Operation to update the state
step = tf.group(U.assign(U_), Ut.assign(Ut_))
# Initialize state to initial conditions
tf.initialize_all_variables().run()
# Run 1000 steps of PDE
for i in range(1000):
# Step simulation
step.run({eps: 0.03, damping: 0.04})
# Visualize every 50 steps
if i % 500 == 0:
plt.imshow(U.eval())
plt.show()Các đồ thị được vẽ như hình dưới đây -
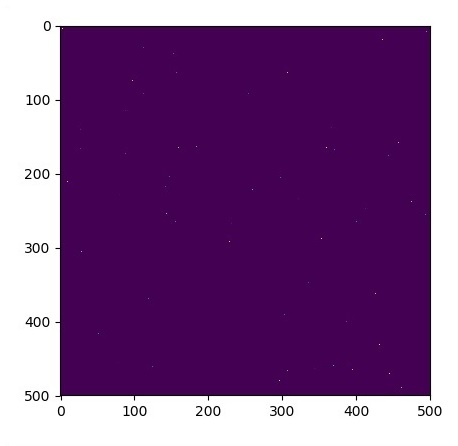
TensorFlow bao gồm một tính năng đặc biệt là nhận dạng hình ảnh và những hình ảnh này được lưu trữ trong một thư mục cụ thể. Với các hình ảnh tương đối giống nhau, sẽ dễ dàng thực hiện logic này cho các mục đích bảo mật.
Cấu trúc thư mục của việc triển khai mã nhận dạng hình ảnh như dưới đây:
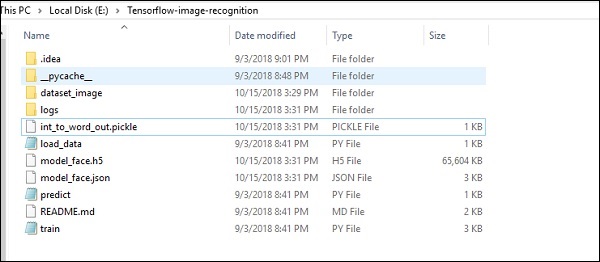
Dataset_image bao gồm các hình ảnh liên quan cần được tải. Chúng tôi sẽ tập trung vào nhận dạng hình ảnh với logo của chúng tôi được xác định trong đó. Các hình ảnh được tải bằng tập lệnh “load_data.py”, giúp ghi chú về các mô-đun nhận dạng hình ảnh khác nhau bên trong chúng.
import pickle
from sklearn.model_selection import train_test_split
from scipy import misc
import numpy as np
import os
label = os.listdir("dataset_image")
label = label[1:]
dataset = []
for image_label in label:
images = os.listdir("dataset_image/"+image_label)
for image in images:
img = misc.imread("dataset_image/"+image_label+"/"+image)
img = misc.imresize(img, (64, 64))
dataset.append((img,image_label))
X = []
Y = []
for input,image_label in dataset:
X.append(input)
Y.append(label.index(image_label))
X = np.array(X)
Y = np.array(Y)
X_train,y_train, = X,Y
data_set = (X_train,y_train)
save_label = open("int_to_word_out.pickle","wb")
pickle.dump(label, save_label)
save_label.close()Việc đào tạo các hình ảnh giúp lưu trữ các mẫu dễ nhận biết trong thư mục được chỉ định.
import numpy
import matplotlib.pyplot as plt
from keras.layers import Dropout
from keras.layers import Flatten
from keras.constraints import maxnorm
from keras.optimizers import SGD
from keras.layers import Conv2D
from keras.layers.convolutional import MaxPooling2D
from keras.utils import np_utils
from keras import backend as K
import load_data
from keras.models import Sequential
from keras.layers import Dense
import keras
K.set_image_dim_ordering('tf')
# fix random seed for reproducibility
seed = 7
numpy.random.seed(seed)
# load data
(X_train,y_train) = load_data.data_set
# normalize inputs from 0-255 to 0.0-1.0
X_train = X_train.astype('float32')
#X_test = X_test.astype('float32')
X_train = X_train / 255.0
#X_test = X_test / 255.0
# one hot encode outputs
y_train = np_utils.to_categorical(y_train)
#y_test = np_utils.to_categorical(y_test)
num_classes = y_train.shape[1]
# Create the model
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape = (64, 64, 3), padding = 'same',
activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.2))
model.add(Conv2D(32, (3, 3), activation = 'relu', padding = 'same',
kernel_constraint = maxnorm(3)))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Flatten())
model.add(Dense(512, activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation = 'softmax'))
# Compile model
epochs = 10
lrate = 0.01
decay = lrate/epochs
sgd = SGD(lr = lrate, momentum = 0.9, decay = decay, nesterov = False)
model.compile(loss = 'categorical_crossentropy', optimizer = sgd, metrics = ['accuracy'])
print(model.summary())
#callbacks = [keras.callbacks.EarlyStopping(
monitor = 'val_loss', min_delta = 0, patience = 0, verbose = 0, mode = 'auto')]
callbacks = [keras.callbacks.TensorBoard(log_dir='./logs',
histogram_freq = 0, batch_size = 32, write_graph = True, write_grads = False,
write_images = True, embeddings_freq = 0, embeddings_layer_names = None,
embeddings_metadata = None)]
# Fit the model
model.fit(X_train, y_train, epochs = epochs,
batch_size = 32,shuffle = True,callbacks = callbacks)
# Final evaluation of the model
scores = model.evaluate(X_train, y_train, verbose = 0)
print("Accuracy: %.2f%%" % (scores[1]*100))
# serialize model to JSONx
model_json = model.to_json()
with open("model_face.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model.save_weights("model_face.h5")
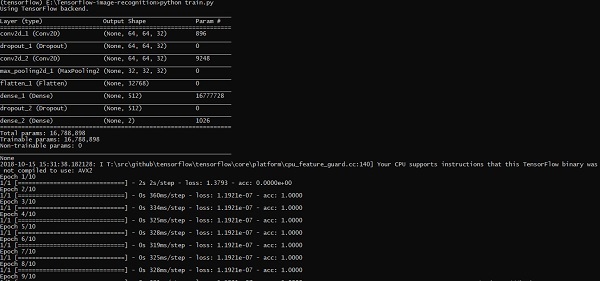
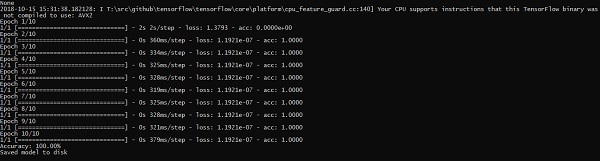
print("Saved model to disk")Dòng mã trên tạo ra kết quả như hình dưới đây:
Trong chương này, chúng ta sẽ hiểu các khía cạnh khác nhau của đào tạo mạng nơron có thể được thực hiện bằng cách sử dụng khung TensorFlow.
Sau đây là mười khuyến nghị, có thể được đánh giá:
Lan truyền ngược
Truyền ngược là một phương pháp đơn giản để tính các đạo hàm riêng, bao gồm dạng cấu tạo cơ bản phù hợp nhất với mạng nơron.
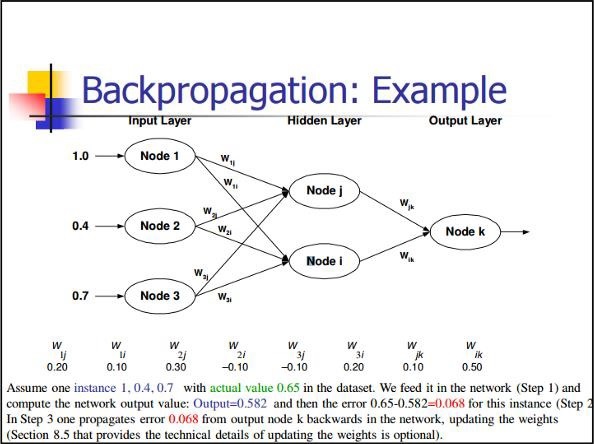
Stochastic Gradient Descent
Trong dốc nghiêng ngẫu nhiên, a batchlà tổng số ví dụ mà người dùng sử dụng để tính toán gradient trong một lần lặp. Cho đến nay, người ta cho rằng lô là toàn bộ tập dữ liệu. Minh họa tốt nhất là hoạt động ở quy mô Google; tập dữ liệu thường chứa hàng tỷ hoặc thậm chí hàng trăm tỷ ví dụ.
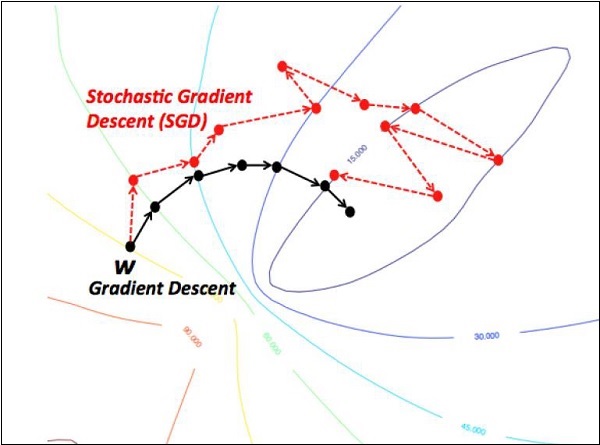
Tỷ lệ học tập giảm sút
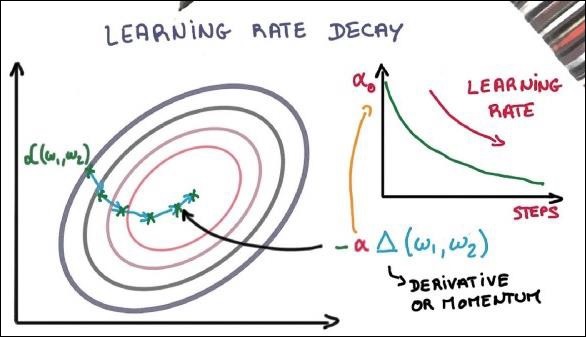
Điều chỉnh tốc độ học tập là một trong những tính năng quan trọng nhất của tối ưu hóa độ dốc. Điều này rất quan trọng đối với việc triển khai TensorFlow.
Rơi ra ngoài
Lưới thần kinh sâu với một số lượng lớn các tham số tạo thành hệ thống học máy mạnh mẽ. Tuy nhiên, quá phù hợp là một vấn đề nghiêm trọng trong các mạng như vậy.

Tổng hợp tối đa
Tổng hợp tối đa là một quá trình tùy biến dựa trên mẫu. Đối tượng là lấy mẫu xuống một biểu diễn đầu vào, điều này làm giảm kích thước với các giả định bắt buộc.

Bộ nhớ ngắn hạn dài hạn (LSTM)
LSTM kiểm soát quyết định về những đầu vào nào nên được thực hiện trong nơ-ron được chỉ định. Nó bao gồm việc kiểm soát việc quyết định những gì nên được tính toán và những gì đầu ra nên được tạo ra.