TensorFlow - Perceptron một lớp

Để hiểu được perceptron lớp đơn, điều quan trọng là phải hiểu Mạng thần kinh nhân tạo (ANN). Mạng nơron nhân tạo là hệ thống xử lý thông tin mà cơ chế của nó được lấy cảm hứng từ các chức năng của các mạch thần kinh sinh học. Một mạng nơ-ron nhân tạo sở hữu nhiều đơn vị xử lý được kết nối với nhau. Sau đây là biểu diễn giản đồ của mạng nơron nhân tạo:

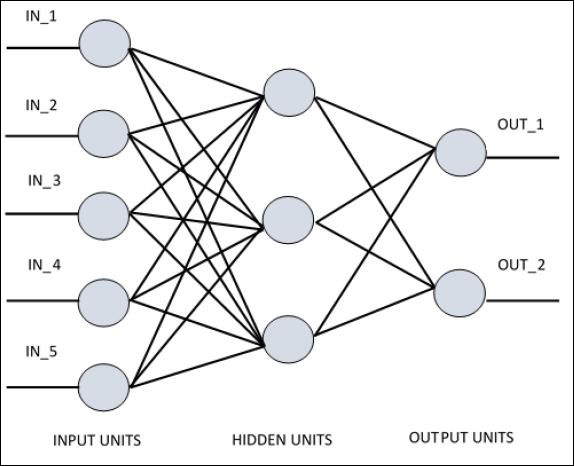
Biểu đồ cho thấy rằng các đơn vị ẩn giao tiếp với lớp bên ngoài. Trong khi các đơn vị đầu vào và đầu ra chỉ giao tiếp thông qua lớp ẩn của mạng.

Mô hình kết nối với các nút, tổng số lớp và mức độ của các nút giữa đầu vào và đầu ra với số lượng tế bào thần kinh trên mỗi lớp xác định kiến trúc của mạng thần kinh.

Có hai kiểu kiến trúc. Các loại này tập trung vào các mạng nơron nhân tạo có chức năng như sau:

Perceptron một lớp
Perceptron nhiều lớp

Perceptron một lớp

Perceptron lớp đơn là mô hình thần kinh được đề xuất đầu tiên được tạo ra. Nội dung của bộ nhớ cục bộ của nơ-ron bao gồm một vectơ trọng số. Việc tính toán một perceptron lớp đơn được thực hiện dựa trên phép tính tổng của mỗi vectơ đầu vào với giá trị nhân với phần tử tương ứng của vectơ của các trọng số. Giá trị được hiển thị trong đầu ra sẽ là đầu vào của một chức năng kích hoạt.

Chúng ta hãy tập trung vào việc triển khai perceptron lớp đơn cho vấn đề phân loại ảnh bằng TensorFlow. Ví dụ tốt nhất để minh họa perceptron lớp đơn là thông qua biểu diễn "Hồi quy logistic".

Bây giờ, chúng ta hãy xem xét các bước cơ bản sau đây của đào tạo hồi quy logistic -

Các trọng số được khởi tạo với các giá trị ngẫu nhiên khi bắt đầu huấn luyện.
Đối với mỗi phần tử của tập huấn luyện, sai số được tính toán với sự khác biệt giữa đầu ra mong muốn và đầu ra thực tế. Sai số được tính toán được sử dụng để điều chỉnh trọng số.
Quá trình được lặp lại cho đến khi lỗi thực hiện trên toàn bộ tập huấn luyện không nhỏ hơn ngưỡng đã chỉ định, cho đến khi đạt đến số lần lặp tối đa.

Mã hoàn chỉnh để đánh giá hồi quy logistic được đề cập dưới đây:

# Import MINST data 
from tensorflow.examples.tutorials.mnist import input_data 
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True) 

import tensorflow as tf 
import matplotlib.pyplot as plt 

# Parameters 
learning_rate = 0.01 
training_epochs = 25 
batch_size = 100 
display_step = 1 

# tf Graph Input 
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784 
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes 

# Create model 
# Set model weights 
W = tf.Variable(tf.zeros([784, 10])) 
b = tf.Variable(tf.zeros([10])) 

# Construct model 
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax 

# Minimize error using cross entropy 
cross_entropy = y*tf.log(activation) 
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1)) 

optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost) 

#Plot settings 
avg_set = [] 
epoch_set = [] 

# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph 
with tf.Session() as sess:
   sess.run(init)
   
   # Training cycle
   for epoch in range(training_epochs):
      avg_cost = 0.
      total_batch = int(mnist.train.num_examples/batch_size)
      
      # Loop over all batches
      for i in range(total_batch):
         batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
         # Fit training using batch data sess.run(optimizer, \ feed_dict = {
            x: batch_xs, y: batch_ys}) 
         # Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
            x: batch_xs, \ y: batch_ys})/total_batch
      # Display logs per epoch step
      if epoch % display_step == 0:
         print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
            avg_set.append(avg_cost) epoch_set.append(epoch+1)
   print ("Training phase finished")
    
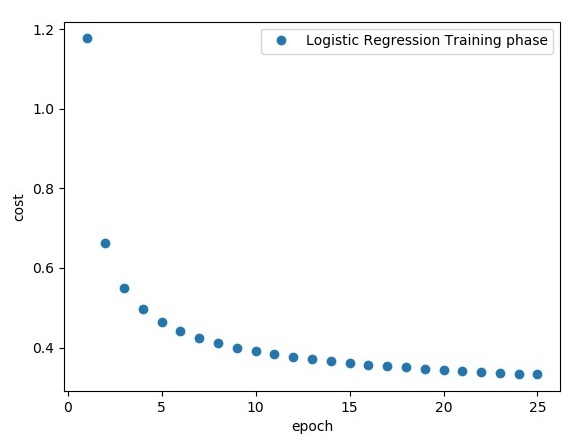
   plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase') 
   plt.ylabel('cost') 
   plt.xlabel('epoch') 
   plt.legend() 
   plt.show() 
    
   # Test model 
   correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1)) 
   
   # Calculate accuracy 
   accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print 
      ("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))

Đầu ra

Đoạn mã trên tạo ra kết quả sau:

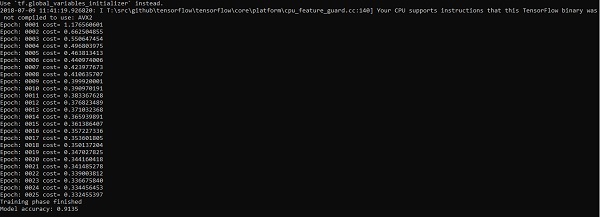
Hồi quy logistic được coi là một phân tích dự báo. Hồi quy logistic được sử dụng để mô tả dữ liệu và giải thích mối quan hệ giữa một biến nhị phân phụ thuộc và một hoặc nhiều biến danh nghĩa hoặc độc lập.