Apache MXNet - Python-Pakete
In diesem Kapitel erfahren Sie mehr über die in Apache MXNet verfügbaren Python-Pakete.
Wichtige MXNet Python-Pakete
MXNet verfügt über die folgenden wichtigen Python-Pakete, die wir einzeln diskutieren werden:
Autograd (automatische Differenzierung)
NDArray
KVStore
Gluon
Visualization
Beginnen wir zuerst mit Autograd Python-Paket für Apache MXNet.
Autograd
Autograd steht für automatic differentiationwird verwendet, um die Gradienten von der Verlustmetrik zurück zu jedem der Parameter zu propagieren. Zusammen mit der Backpropagation wird ein dynamischer Programmieransatz verwendet, um die Gradienten effizient zu berechnen. Es wird auch als automatische Differenzierung im umgekehrten Modus bezeichnet. Diese Technik ist sehr effizient in Fan-In-Situationen, in denen viele Parameter eine einzelne Verlustmetrik beeinflussen.
Was sind Farbverläufe?
Gradienten sind die Grundlagen für den Prozess des neuronalen Netzwerktrainings. Sie erklären uns im Grunde, wie wir die Parameter des Netzwerks ändern können, um seine Leistung zu verbessern.
Wie wir wissen, bestehen neuronale Netze (NN) aus Operatoren wie Summen, Produkten, Faltungen usw. Diese Operatoren verwenden für ihre Berechnungen Parameter wie die Gewichte in Faltungskernen. Wir sollten die optimalen Werte für diese Parameter finden müssen, und Gradienten zeigen uns den Weg und führen uns auch zur Lösung.
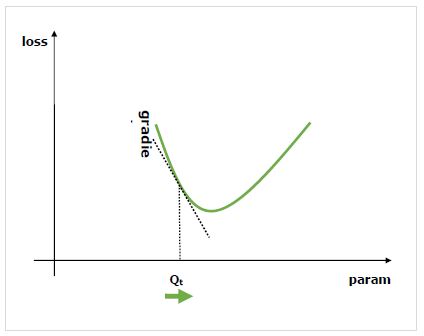
Wir sind an der Auswirkung der Änderung eines Parameters auf die Leistung des Netzwerks interessiert, und Gradienten geben an, um wie viel eine bestimmte Variable zunimmt oder abnimmt, wenn wir eine Variable ändern, von der sie abhängt. Die Leistung wird normalerweise mithilfe einer Verlustmetrik definiert, die wir zu minimieren versuchen. Zum Beispiel könnten wir für die Regression versuchen, zu minimierenL2 Verlust zwischen unseren Vorhersagen und dem genauen Wert, während wir für die Klassifizierung die minimieren könnten cross-entropy loss.
Sobald wir den Gradienten jedes Parameters in Bezug auf den Verlust berechnet haben, können wir einen Optimierer verwenden, z. B. den stochastischen Gradientenabstieg.
Wie berechnet man Farbverläufe?
Wir haben die folgenden Optionen, um Farbverläufe zu berechnen:
Symbolic Differentiation- Die allererste Option ist die symbolische Differenzierung, bei der die Formeln für jeden Gradienten berechnet werden. Der Nachteil dieser Methode ist, dass sie schnell zu unglaublich langen Formeln führt, wenn das Netzwerk tiefer und die Bediener komplexer werden.
Finite Differencing- Eine andere Möglichkeit besteht darin, eine endliche Differenzierung zu verwenden, bei der geringfügige Unterschiede für jeden Parameter versucht werden und die Reaktion der Verlustmetrik überprüft wird. Der Nachteil dieses Verfahrens besteht darin, dass es rechenintensiv wäre und möglicherweise eine schlechte numerische Genauigkeit aufweist.
Automatic differentiation- Die Lösung für die Nachteile der oben genannten Methoden besteht darin, die Gradienten von der Verlustmetrik zurück zu jedem der Parameter zu verwenden, indem eine automatische Differenzierung verwendet wird. Die Ausbreitung ermöglicht uns einen dynamischen Programmieransatz zur effizienten Berechnung der Gradienten. Diese Methode wird auch als automatische Differenzierung im umgekehrten Modus bezeichnet.
Automatische Differenzierung (autograd)
Hier werden wir die Arbeitsweise von Autograd im Detail verstehen. Es funktioniert grundsätzlich in zwei Schritten:
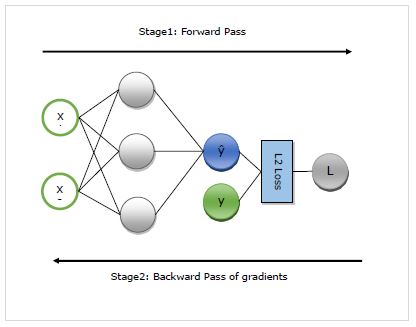
Stage 1 - Diese Stufe heißt ‘Forward Pass’des Trainings. Wie der Name schon sagt, wird in dieser Phase die Aufzeichnung des Betreibers erstellt, der vom Netzwerk verwendet wird, um Vorhersagen zu treffen und die Verlustmetrik zu berechnen.
Stage 2 - Diese Stufe heißt ‘Backward Pass’des Trainings. Wie der Name schon sagt, funktioniert es in dieser Phase rückwärts durch diesen Datensatz. Wenn Sie rückwärts gehen, werden die partiellen Ableitungen jedes Operators bis zum Netzwerkparameter ausgewertet.
Vorteile von Autograd
Im Folgenden sind die Vorteile der automatischen Differenzierung (Autograd) aufgeführt:
Flexible- Flexibilität, die wir bei der Definition unseres Netzwerks erhalten, ist einer der großen Vorteile der Verwendung von Autograd. Wir können die Operationen bei jeder Iteration ändern. Diese werden als dynamische Diagramme bezeichnet, deren Implementierung in Frameworks, die statische Diagramme erfordern, viel komplexer ist. Selbst in solchen Fällen kann Autograd die Farbverläufe immer noch korrekt zurückpropagieren.
Automatic- Autograd ist automatisch, dh die Komplexität des Backpropagation-Verfahrens wird von Ihnen für Sie erledigt. Wir müssen nur angeben, welche Verläufe wir berechnen möchten.
Efficient - Autogard berechnet die Farbverläufe sehr effizient.
Can use native Python control flow operators- Wir können die nativen Python-Steuerungsflussoperatoren verwenden, z. B. if-Bedingung und while-Schleife. Der Autograd kann die Gradienten weiterhin effizient und korrekt zurückpropagieren.
Verwenden von Autograd in MXNet Gluon
Hier sehen wir anhand eines Beispiels, wie wir es verwenden können autograd in MXNet Gluon.
Implementierungsbeispiel
Im folgenden Beispiel implementieren wir das Regressionsmodell mit zwei Ebenen. Nach der Implementierung verwenden wir Autograd, um den Gradienten des Verlusts unter Bezugnahme auf jeden der Gewichtsparameter automatisch zu berechnen.
Importieren Sie zuerst den Autogrard und andere erforderliche Pakete wie folgt:
from mxnet import autograd
import mxnet as mx
from mxnet.gluon.nn import HybridSequential, Dense
from mxnet.gluon.loss import L2LossJetzt müssen wir das Netzwerk wie folgt definieren:
N_net = HybridSequential()
N_net.add(Dense(units=3))
N_net.add(Dense(units=1))
N_net.initialize()Jetzt müssen wir den Verlust wie folgt definieren:
loss_function = L2Loss()Als nächstes müssen wir die Dummy-Daten wie folgt erstellen:
x = mx.nd.array([[0.5, 0.9]])
y = mx.nd.array([[1.5]])Jetzt sind wir bereit für unseren ersten Vorwärtsdurchlauf durch das Netzwerk. Wir möchten, dass Autograd den Rechengraphen aufzeichnet, damit wir die Gradienten berechnen können. Dazu müssen wir den Netzwerkcode im Umfang von ausführenautograd.record Kontext wie folgt -
with autograd.record():
y_hat = N_net(x)
loss = loss_function(y_hat, y)Jetzt sind wir bereit für den Rückwärtsdurchlauf, bei dem wir zunächst die Rückwärtsmethode für die interessierende Menge aufrufen. Die Quatität des Interesses in unserem Beispiel ist Verlust, weil wir versuchen, den Verlustgradienten unter Bezugnahme auf die Parameter zu berechnen -
loss.backward()Jetzt haben wir Gradienten für jeden Parameter des Netzwerks, die vom Optimierer verwendet werden, um den Parameterwert für eine verbesserte Leistung zu aktualisieren. Schauen wir uns die Farbverläufe der 1. Ebene wie folgt an:
N_net[0].weight.grad()Output
Die Ausgabe ist wie folgt
[[-0.00470527 -0.00846948]
[-0.03640365 -0.06552657]
[ 0.00800354 0.01440637]]
<NDArray 3x2 @cpu(0)>Vollständiges Implementierungsbeispiel
Im Folgenden finden Sie das vollständige Implementierungsbeispiel.
from mxnet import autograd
import mxnet as mx
from mxnet.gluon.nn import HybridSequential, Dense
from mxnet.gluon.loss import L2Loss
N_net = HybridSequential()
N_net.add(Dense(units=3))
N_net.add(Dense(units=1))
N_net.initialize()
loss_function = L2Loss()
x = mx.nd.array([[0.5, 0.9]])
y = mx.nd.array([[1.5]])
with autograd.record():
y_hat = N_net(x)
loss = loss_function(y_hat, y)
loss.backward()
N_net[0].weight.grad()