Grundlagen von Computern - Zahlensystem
Die Technik zum Darstellen und Arbeiten mit Zahlen wird aufgerufen number system. Decimal number systemist das gebräuchlichste Zahlensystem. Andere beliebte Zahlensysteme umfassen binary number system, octal number system, hexadecimal number system, etc.
Dezimalzahlensystem
Das Dezimalzahlensystem ist a base 10Zahlensystem mit 10 Ziffern von 0 bis 9. Dies bedeutet, dass jede numerische Größe mit diesen 10 Ziffern dargestellt werden kann. Das Dezimalzahlensystem ist auch einpositional value system. Dies bedeutet, dass der Wert der Ziffern von seiner Position abhängt. Nehmen wir ein Beispiel, um dies zu verstehen.
Angenommen, wir haben drei Zahlen - 734, 971 und 207. Der Wert 7 in allen drei Zahlen ist unterschiedlich
- In 734 beträgt der Wert 7 7 Hundert oder 700 oder 7 × 100 oder 7 × 10 2
- In 971 beträgt der Wert 7 7 Zehner oder 70 oder 7 × 10 oder 7 × 10 1
- In 207 ist der Wert 0f 7 7 Einheiten oder 7 oder 7 × 1 oder 7 × 10 0
Die Gewichtung jeder Position kann wie folgt dargestellt werden:

In digitalen Systemen werden Anweisungen durch elektrische Signale gegeben; Die Variation erfolgt durch Variation der Spannung des Signals. Es ist schwierig, 10 verschiedene Spannungen zu haben, um ein Dezimalzahlensystem in digitalen Geräten zu implementieren. Daher wurden viele Zahlensysteme entwickelt, die einfacher digital zu implementieren sind. Schauen wir sie uns genauer an.
Binärzahlensystem
Der einfachste Weg, Anweisungen durch elektrische Signale zu variieren, ist das Zwei-Zustands-System - Ein und Aus. Ein wird als 1 und Aus als 0 dargestellt, obwohl 0 eigentlich kein Signal ist, sondern ein Signal mit einer niedrigeren Spannung. Das Zahlensystem mit nur diesen beiden Ziffern - 0 und 1 - wird aufgerufenbinary number system.
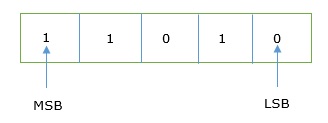
Jede Binärziffer wird auch als a bezeichnet bit. Das Binärzahlensystem ist auch ein Positionswertsystem, bei dem jede Ziffer einen Wert in Zweierpotenzen hat, wie hier angezeigt.

In jeder Binärzahl wird die am weitesten rechts stehende Ziffer aufgerufen least significant bit (LSB) und die am weitesten links stehende Ziffer wird aufgerufen most significant bit (MSB).
Das Dezimaläquivalent dieser Zahl ist die Summe der Produkte jeder Ziffer mit ihrem Positionswert.
11010 2 = 1 × 2 4 + 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
= 16 + 8 + 0 + 2 + 0
= 26 10
Der Computerspeicher wird anhand der Anzahl der gespeicherten Bits gemessen. Hier ist ein Diagramm für die Konvertierung der Speicherkapazität.
- 1 Byte (B) = 8 Bits
- 1 Kilobyte (KB) = 1024 Byte
- 1 Megabyte (MB) = 1024 KB
- 1 Gigabyte (GB) = 1024 MB
- 1 Terabyte (TB) = 1024 GB
- 1 Exabyte (EB) = 1024 PB
- 1 Zettabyte = 1024 EB
- 1 Yottabyte (YB) = 1024 ZB
Oktalzahlensystem
Octal number system hat acht Ziffern - 0, 1, 2, 3, 4, 5, 6 und 7. Das Oktalzahlensystem ist auch ein Positionswertsystem, bei dem jede Ziffer ihren Wert in Potenzen von 8 ausdrückt, wie hier gezeigt -

Das Dezimaläquivalent einer Oktalzahl ist die Summe der Produkte jeder Ziffer mit ihrem Positionswert.
726 8 = 7 × 8 2 + 2 × 8 1 + 6 × 8 0
= 448 + 16 + 6
= 470 10
Hexadezimalzahlensystem
Octal number system hat 16 Symbole - 0 bis 9 und A bis F, wobei A gleich 10 ist, B gleich 11 ist und so weiter bis F. Das Hexadezimalzahlensystem ist auch ein Positionswertsystem, bei dem jede Ziffer ihren Wert in Potenzen von 16 ausgedrückt hat , wie hier gezeigt -

Das Dezimaläquivalent einer Hexadezimalzahl ist die Summe der Produkte jeder Ziffer mit ihrem Positionswert.
27FB 16 = 2 × 16 3 + 7 × 16 2 + 15 × 16 1 + 10 × 16 0
= 8192 + 1792 + 240 + 10
= 10234 10
Zahlensystembeziehung
Die folgende Tabelle zeigt die Beziehung zwischen Dezimal-, Binär-, Oktal- und Hexadezimalzahlensystemen.
| HEXADEZIMAL | DEZIMAL | OKTAL | BINÄR |
|---|---|---|---|
| 0 | 0 | 0 | 0000 |
| 1 | 1 | 1 | 0001 |
| 2 | 2 | 2 | 0010 |
| 3 | 3 | 3 | 0011 |
| 4 | 4 | 4 | 0100 |
| 5 | 5 | 5 | 0101 |
| 6 | 6 | 6 | 0110 |
| 7 | 7 | 7 | 0111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| EIN | 10 | 12 | 1010 |
| B. | 11 | 13 | 1011 |
| C. | 12 | 14 | 1100 |
| D. | 13 | 15 | 1101 |
| E. | 14 | 16 | 1110 |
| F. | 15 | 17 | 1111 |
ASCII
Neben numerischen Daten muss der Computer in der Lage sein, Alphabete, Satzzeichen, mathematische Operatoren, spezielle Symbole usw. zu verarbeiten, die den vollständigen Zeichensatz der englischen Sprache bilden. Der gesamte Satz von Zeichen oder Symbolen wird als alphanumerische Codes bezeichnet. Der vollständige alphanumerische Code enthält normalerweise -
- 26 Großbuchstaben
- 26 Kleinbuchstaben
- 10 Ziffern
- 7 Satzzeichen
- 20 bis 40 Sonderzeichen
Jetzt versteht ein Computer nur numerische Werte, unabhängig vom verwendeten Zahlensystem. Daher müssen alle Zeichen ein numerisches Äquivalent haben, das als alphanumerischer Code bezeichnet wird. Der am häufigsten verwendete alphanumerische Code ist der amerikanische Standardcode für den Informationsaustausch (ASCII). ASCII ist ein 7-Bit-Code mit 128 (27) möglichen Codes.

ISCII
ISCII steht für Indian Script Code for Information Interchange. IISCII wurde entwickelt, um indische Sprachen am Computer zu unterstützen. Zu den von IISCI unterstützten Sprachen gehören Devanagari, Tamil, Bangla, Gujarati, Gurmukhi, Tamil, Telugu usw. IISCI wird hauptsächlich von Regierungsabteilungen verwendet und bevor es sich durchsetzen kann, wird ein neuer universeller Kodierungsstandard genanntUnicode wurde vorgestellt.
Unicode
Unicode ist ein internationales Codierungssystem, das für die Verwendung mit verschiedenen Sprachskripten entwickelt wurde. Jedem Zeichen oder Symbol wird ein eindeutiger numerischer Wert zugewiesen, weitgehend im Rahmen von ASCII. Zuvor hatte jedes Skript ein eigenes Codierungssystem, das miteinander in Konflikt stehen konnte.
Im Gegensatz dazu ist dies das, was Unicode offiziell anstrebt - Unicode bietet eine eindeutige Nummer für jeden Charakter, unabhängig von der Plattform, unabhängig vom Programm und der Sprache .