Fläche eines Kreises
Die Fläche eines Kreises ist die Ausdehnung des Inneren eines Kreises.
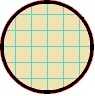
Die Fläche eines Kreises ist die Anzahl der quadratischen Einheiten innerhalb dieses Kreises. Wenn jedes Quadrat im Kreis unten eine Fläche von 1 cm 2 hat , können wir die Gesamtzahl der Quadrate zählen, um die Fläche dieses Kreises zu erhalten. Wenn es also insgesamt 28,24 Quadrate gäbe, wäre die Fläche dieses Kreises 28,24 cm 2
Es ist jedoch einfacher, eine der folgenden Formeln zu verwenden:
Formula for Area of a Circle
Die Fläche eines Kreises ist durch die Formel A = πr 2 gegeben, wobei π = 3,14 und r der Radius des Kreises ist.
Fläche eines Kreises ist durch die Formel A = & pgr; D gegeben 2 /4 , wobei π = 3,14 und d der Durchmesser des Kreises ist.
Suchen Sie den Bereich des folgenden Kreises. Verwenden Sie π = 3,14

Lösung
Step 1:
Gegebener Durchmesser = 13; Radius r = 13/2 = 6,5 Einheiten
Step 2:
Kreisfläche = πr 2 = (3,14) (6,5) (6,5) = 132,67 quadratische Einheiten
Suchen Sie den Bereich des folgenden Kreises. Verwenden Sie π = 3,14
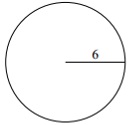
Lösung
Step 1:
Gegebener Radius r = 6 Einheiten
Step 2:
Kreisfläche = πr 2 = (3,14) (6) (6) = 113,04 quadratische Einheiten