Deep Learning mit Keras - Kurzanleitung

Deep Learning ist in den letzten Tagen zu einem Schlagwort auf dem Gebiet der künstlichen Intelligenz (KI) geworden. Seit vielen Jahren verwenden wir maschinelles Lernen (ML), um Maschinen Intelligenz zu vermitteln. In den letzten Tagen ist Deep Learning aufgrund seiner Überlegenheit bei Vorhersagen im Vergleich zu herkömmlichen ML-Techniken immer beliebter geworden.

Deep Learning bedeutet im Wesentlichen, ein künstliches neuronales Netzwerk (ANN) mit einer großen Datenmenge zu trainieren. Beim Deep Learning lernt das Netzwerk von selbst und benötigt daher riesige Daten zum Lernen. Während traditionelles maschinelles Lernen im Wesentlichen eine Reihe von Algorithmen ist, die Daten analysieren und daraus lernen. Sie nutzten dieses Lernen dann, um intelligente Entscheidungen zu treffen.

Bei Keras handelt es sich um eine API für neuronale Netze auf hoher Ebene, die auf TensorFlow ausgeführt wird - einer durchgängigen Open-Source-Plattform für maschinelles Lernen. Mit Keras können Sie auf einfache Weise komplexe ANN-Architekturen definieren, um mit Ihren Big Data zu experimentieren. Keras unterstützt auch die GPU, die für die Verarbeitung großer Datenmengen und die Entwicklung von Modellen für maschinelles Lernen unerlässlich ist.

In diesem Tutorial lernen Sie die Verwendung von Keras beim Aufbau tiefer neuronaler Netze. Wir werden uns die praktischen Beispiele für den Unterricht ansehen. Das vorliegende Problem besteht darin, handgeschriebene Ziffern mithilfe eines neuronalen Netzwerks zu erkennen, das mit tiefem Lernen trainiert wird.

Im Folgenden finden Sie einen Screenshot der Google-Trends zum Thema Deep Learning.

Wie Sie dem Diagramm entnehmen können, wächst das Interesse an Deep Learning in den letzten Jahren stetig. Es gibt viele Bereiche wie Computer Vision, Verarbeitung natürlicher Sprache, Spracherkennung, Bioinformatik, Arzneimitteldesign usw., in denen das tiefe Lernen erfolgreich angewendet wurde. Mit diesem Tutorial können Sie schnell mit dem vertieften Lernen beginnen.

Also lies weiter!

Wie in der Einleitung erwähnt, ist Deep Learning ein Prozess zum Trainieren eines künstlichen neuronalen Netzwerks mit einer großen Datenmenge. Nach dem Training kann das Netzwerk uns Vorhersagen zu unsichtbaren Daten geben. Bevor ich weiter erkläre, was tiefes Lernen ist, lassen Sie uns kurz einige Begriffe durchgehen, die beim Training eines neuronalen Netzwerks verwendet werden.

Neuronale Netze

Die Idee des künstlichen neuronalen Netzwerks wurde von neuronalen Netzwerken in unserem Gehirn abgeleitet. Ein typisches neuronales Netzwerk besteht aus drei Schichten - Eingabe, Ausgabe und versteckte Schicht, wie in der folgenden Abbildung gezeigt.

Dies wird auch als a bezeichnet shallowneuronales Netzwerk, da es nur eine verborgene Schicht enthält. Sie fügen der obigen Architektur mehr versteckte Ebenen hinzu, um eine komplexere Architektur zu erstellen.

Tiefe Netzwerke

Das folgende Diagramm zeigt ein tiefes Netzwerk, das aus vier verborgenen Schichten, einer Eingangsschicht und einer Ausgangsschicht besteht.

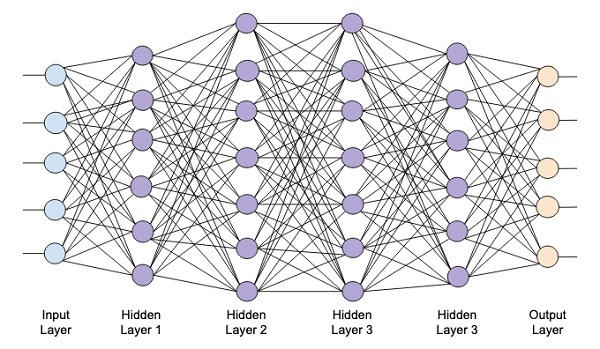
Wenn dem Netzwerk die Anzahl der verborgenen Schichten hinzugefügt wird, wird das Training in Bezug auf die erforderlichen Ressourcen und die Zeit, die zum vollständigen Trainieren des Netzwerks erforderlich ist, komplexer.

Netzwerktraining

Nachdem Sie die Netzwerkarchitektur definiert haben, trainieren Sie sie für bestimmte Arten von Vorhersagen. Das Trainieren eines Netzwerks ist ein Prozess zum Finden der richtigen Gewichte für jede Verbindung im Netzwerk. Während des Trainings fließen die Daten von den Eingabe- zu den Ausgabeebenen durch verschiedene verborgene Ebenen. Da sich die Daten von Eingabe zu Ausgabe immer in eine Richtung bewegen, bezeichnen wir dieses Netzwerk als Feed-Forward-Netzwerk und die Datenausbreitung als Forward-Propagation.

Aktivierungsfunktion

Auf jeder Ebene berechnen wir die gewichtete Summe der Eingaben und geben sie an eine Aktivierungsfunktion weiter. Die Aktivierungsfunktion bringt Nichtlinearität in das Netzwerk. Es ist einfach eine mathematische Funktion, die die Ausgabe diskretisiert. Einige der am häufigsten verwendeten Aktivierungsfunktionen sind Sigmoid, Hyperbolic, Tangent (Tanh), ReLU und Softmax.

Backpropagation

Backpropagation ist ein Algorithmus für überwachtes Lernen. Bei der Backpropagation breiten sich die Fehler von der Ausgabe zur Eingabeebene rückwärts aus. Bei gegebener Fehlerfunktion berechnen wir den Gradienten der Fehlerfunktion in Bezug auf die bei jeder Verbindung zugewiesenen Gewichte. Die Berechnung des Gradienten erfolgt rückwärts durch das Netzwerk. Der Gradient der letzten Gewichtsschicht wird zuerst berechnet und der Gradient der ersten Gewichtsschicht wird zuletzt berechnet.

In jeder Schicht werden die Teilberechnungen des Gradienten bei der Berechnung des Gradienten für die vorherige Schicht wiederverwendet. Dies wird als Gradientenabstieg bezeichnet.

In diesem projektbasierten Lernprogramm definieren Sie ein tiefes neuronales Feed-Forward-Netzwerk und trainieren es mit Backpropagation- und Gradientenabstiegstechniken. Glücklicherweise bietet Keras uns alle APIs auf hoher Ebene, um die Netzwerkarchitektur zu definieren und sie mithilfe des Gradientenabfalls zu trainieren. Als Nächstes erfahren Sie, wie Sie dies in Keras tun.

Handschriftliches Ziffernerkennungssystem

In diesem Miniprojekt wenden Sie die zuvor beschriebenen Techniken an. Sie erstellen ein tief lernendes neuronales Netzwerk, das für das Erkennen handgeschriebener Ziffern trainiert wird. In jedem maschinellen Lernprojekt besteht die erste Herausforderung darin, die Daten zu sammeln. Insbesondere für Deep-Learning-Netzwerke benötigen Sie umfangreiche Daten. Glücklicherweise hat für das Problem, das wir zu lösen versuchen, bereits jemand einen Datensatz für das Training erstellt. Dies wird als mnist bezeichnet und ist als Teil der Keras-Bibliotheken verfügbar. Der Datensatz besteht aus mehreren 28x28-Pixel-Bildern handgeschriebener Ziffern. Sie trainieren Ihr Modell auf dem Hauptteil dieses Datensatzes und der Rest der Daten wird zur Validierung Ihres trainierten Modells verwendet.

Projektbeschreibung

Das mnistDer Datensatz besteht aus 70000 Bildern handgeschriebener Ziffern. Einige Beispielbilder werden hier als Referenz wiedergegeben

Jedes Bild hat eine Größe von 28 x 28 Pixel, sodass es insgesamt 768 Pixel mit verschiedenen Graustufen aufweist. Die meisten Pixel tendieren zu Schwarz, während nur wenige zu Weiß tendieren. Wir werden die Verteilung dieser Pixel in ein Array oder einen Vektor einfügen. Beispielsweise ist die Verteilung der Pixel für ein typisches Bild der Ziffern 4 und 5 in der folgenden Abbildung dargestellt.

Sie können deutlich sehen, dass die Verteilung der Pixel (insbesondere derjenigen, die zum Weißton tendieren) unterschiedlich ist. Dies unterscheidet die Ziffern, die sie darstellen. Wir werden diese Verteilung von 784 Pixeln als Eingabe in unser Netzwerk einspeisen. Die Ausgabe des Netzwerks besteht aus 10 Kategorien, die eine Ziffer zwischen 0 und 9 darstellen.

Unser Netzwerk wird aus 4 Schichten bestehen - einer Eingangsschicht, einer Ausgangsschicht und zwei versteckten Schichten. Jede verborgene Ebene enthält 512 Knoten. Jede Schicht ist vollständig mit der nächsten Schicht verbunden. Wenn wir das Netzwerk trainieren, berechnen wir die Gewichte für jede Verbindung. Wir trainieren das Netzwerk durch Anwendung von Backpropagation und Gradientenabstieg, die wir zuvor besprochen haben.

Lassen Sie uns vor diesem Hintergrund nun mit der Erstellung des Projekts beginnen.

Projekt einrichten

Wir werden verwenden Jupyter durch AnacondaNavigator für unser Projekt. Da unser Projekt TensorFlow und Keras verwendet, müssen Sie diese im Anaconda-Setup installieren. Führen Sie zum Installieren von Tensorflow den folgenden Befehl in Ihrem Konsolenfenster aus:

>conda install -c anaconda tensorflow

Verwenden Sie den folgenden Befehl, um Keras zu installieren:

>conda install -c anaconda keras

Sie können jetzt Jupyter starten.

Jupyter starten

Wenn Sie den Anaconda-Navigator starten, wird der folgende Startbildschirm angezeigt.

Klicken ‘Jupyter’um es zu starten. Auf dem Bildschirm werden ggf. die vorhandenen Projekte auf Ihrem Laufwerk angezeigt.

Ein neues Projekt starten

Starten Sie ein neues Python 3-Projekt in Anaconda, indem Sie die folgende Menüoption auswählen:

File | New Notebook | Python 3

Der Screenshot der Menüauswahl wird als Kurzreferenz angezeigt -

Ein neues leeres Projekt wird wie unten gezeigt auf Ihrem Bildschirm angezeigt -

Ändern Sie den Projektnamen in DeepLearningDigitRecognition durch Klicken und Bearbeiten des Standardnamens “UntitledXX”.

Wir importieren zuerst die verschiedenen Bibliotheken, die für den Code in unserem Projekt erforderlich sind.

Array-Handhabung und Plotten

Als typisch verwenden wir numpy für Array-Handling und matplotlibzum Plotten. Diese Bibliotheken werden wie folgt in unser Projekt importiertimport Aussagen

import numpy as np
import matplotlib
import matplotlib.pyplot as plot

Warnungen unterdrücken

Da sowohl Tensorflow als auch Keras ständig überarbeitet werden, werden zur Laufzeit zahlreiche Warnfehler angezeigt, wenn Sie die entsprechenden Versionen im Projekt nicht synchronisieren. Da sie Ihre Aufmerksamkeit vom Lernen ablenken, werden wir alle Warnungen in diesem Projekt unterdrücken. Dies geschieht mit den folgenden Codezeilen:

# silent all warnings
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
import warnings
warnings.filterwarnings('ignore')
from tensorflow.python.util import deprecation
deprecation._PRINT_DEPRECATION_WARNINGS = False

Keras

Wir verwenden Keras-Bibliotheken, um Datasets zu importieren. Wir werden die verwendenmnistDatensatz für handschriftliche Ziffern. Wir importieren das erforderliche Paket mit der folgenden Anweisung

from keras.datasets import mnist

Wir werden unser tief lernendes neuronales Netzwerk mithilfe von Keras-Paketen definieren. Wir importieren dieSequential, Dense, Dropout und ActivationPakete zur Definition der Netzwerkarchitektur. Wir gebrauchenload_modelPaket zum Speichern und Abrufen unseres Modells. Wir benützen auchnp_utilsfür ein paar Dienstprogramme, die wir in unserem Projekt benötigen. Diese Importe werden mit den folgenden Programmanweisungen ausgeführt:

from keras.models import Sequential, load_model
from keras.layers.core import Dense, Dropout, Activation
from keras.utils import np_utils

Wenn Sie diesen Code ausführen, wird auf der Konsole eine Meldung angezeigt, dass Keras im Backend TensorFlow verwendet. Der Screenshot zu diesem Zeitpunkt wird hier gezeigt -

Da wir nun alle für unser Projekt erforderlichen Importe haben, werden wir die Architektur für unser Deep Learning-Netzwerk definieren.

Unser neuronales Netzwerkmodell wird aus einem linearen Stapel von Schichten bestehen. Um ein solches Modell zu definieren, nennen wir dasSequential Funktion -

model = Sequential()

Eingabeebene

Wir definieren die Eingabeebene, die die erste Ebene in unserem Netzwerk ist, mithilfe der folgenden Programmanweisung:

model.add(Dense(512, input_shape=(784,)))

Dadurch wird eine Ebene mit 512 Knoten (Neuronen) mit 784 Eingangsknoten erstellt. Dies ist in der folgenden Abbildung dargestellt -

Beachten Sie, dass alle Eingangsknoten vollständig mit der Schicht 1 verbunden sind, dh jeder Eingangsknoten ist mit allen 512 Knoten der Schicht 1 verbunden.

Als nächstes müssen wir die Aktivierungsfunktion für die Ausgabe von Schicht 1 hinzufügen. Wir werden ReLU als unsere Aktivierung verwenden. Die Aktivierungsfunktion wird mit der folgenden Programmanweisung hinzugefügt:

model.add(Activation('relu'))

Als nächstes fügen wir mit der folgenden Anweisung einen Ausfall von 20% hinzu. Dropout ist eine Technik, mit der verhindert wird, dass das Modell überpasst.

model.add(Dropout(0.2))

Zu diesem Zeitpunkt ist unsere Eingabeebene vollständig definiert. Als nächstes werden wir eine versteckte Ebene hinzufügen.

Versteckte Ebene

Unsere verborgene Schicht wird aus 512 Knoten bestehen. Die Eingabe in die verborgene Ebene stammt von unserer zuvor definierten Eingabeebene. Alle Knoten sind wie im vorherigen Fall vollständig verbunden. Die Ausgabe der verborgenen Ebene geht an die nächste Ebene im Netzwerk, die unsere letzte und Ausgabeebene sein wird. Wir werden die gleiche ReLU-Aktivierung wie für die vorherige Schicht und einen Ausfall von 20% verwenden. Der Code zum Hinzufügen dieser Ebene ist hier angegeben -

model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))

Das Netzwerk in dieser Phase kann wie folgt visualisiert werden:

Als nächstes fügen wir die letzte Schicht zu unserem Netzwerk hinzu, die die Ausgabeschicht ist. Beachten Sie, dass Sie mit dem Code, der dem hier verwendeten ähnlich ist, beliebig viele versteckte Ebenen hinzufügen können. Das Hinzufügen weiterer Schichten würde das Netzwerk für das Training komplex machen. In vielen Fällen, wenn auch nicht in allen Fällen, wird ein deutlicher Vorteil aus besseren Ergebnissen erzielt.

Ausgabeschicht

Die Ausgabeebene besteht aus nur 10 Knoten, da wir die angegebenen Bilder in 10 verschiedene Ziffern klassifizieren möchten. Wir fügen diese Ebene mit der folgenden Anweisung hinzu:

model.add(Dense(10))

Da wir die Ausgabe in 10 verschiedene Einheiten klassifizieren möchten, verwenden wir die Softmax-Aktivierung. Bei ReLU ist die Ausgabe binär. Wir fügen die Aktivierung mit der folgenden Anweisung hinzu:

model.add(Activation('softmax'))

Zu diesem Zeitpunkt kann unser Netzwerk wie in der folgenden Abbildung dargestellt visualisiert werden.

Zu diesem Zeitpunkt ist unser Netzwerkmodell vollständig in der Software definiert. Führen Sie die Codezelle aus. Wenn keine Fehler vorliegen, wird auf dem Bildschirm eine Bestätigungsmeldung angezeigt (siehe Abbildung unten).

Als nächstes müssen wir das Modell kompilieren.

Die Kompilierung wird mit einem einzigen aufgerufenen Methodenaufruf durchgeführt compile.

model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')

Das compileMethode erfordert mehrere Parameter. Der Verlustparameter wird als Typ angegeben'categorical_crossentropy'. Der Metrikparameter ist auf eingestellt'accuracy' und schließlich benutzen wir die adamOptimierer für das Training des Netzwerks. Die Ausgabe in dieser Phase ist unten dargestellt -

Jetzt können wir die Daten in unser Netzwerk einspeisen.

Lade Daten

Wie bereits erwähnt, werden wir die verwenden mnistDatensatz von Keras zur Verfügung gestellt. Wenn wir die Daten in unser System laden, teilen wir sie in die Trainings- und Testdaten auf. Die Daten werden durch Aufrufen von geladenload_data Methode wie folgt -

(X_train, y_train), (X_test, y_test) = mnist.load_data()

Die Ausgabe in dieser Phase sieht wie folgt aus:

Nun lernen wir die Struktur des geladenen Datensatzes.

Die Daten, die uns zur Verfügung gestellt werden, sind grafische Bilder mit einer Größe von 28 x 28 Pixel, die jeweils eine einzelne Ziffer zwischen 0 und 9 enthalten. Die ersten zehn Bilder werden auf der Konsole angezeigt. Der Code dafür ist unten angegeben -

# printing first 10 images
for i in range(10):

plot.subplot(3,5,i+1)
plot.tight_layout()
plot.imshow(X_train[i], cmap='gray', interpolation='none')
plot.title("Digit: {}".format(y_train[i]))
plot.xticks([])
plot.yticks([])

In einer iterativen Schleife von 10 Zählungen erstellen wir bei jeder Iteration eine Unterzeichnung und zeigen ein Bild von X_trainVektor darin. Wir benennen jedes Bild aus dem entsprechendeny_trainVektor. Notiere dass dery_train Der Vektor enthält die tatsächlichen Werte für das entsprechende Bild in X_trainVektor. Wir entfernen die Markierungen der x- und y-Achse, indem wir die beiden Methoden aufrufenxticks und yticksmit null Argument. Wenn Sie den Code ausführen, wird die folgende Ausgabe angezeigt:

Als nächstes bereiten wir Daten für die Einspeisung in unser Netzwerk vor.

Bevor wir die Daten in unser Netzwerk einspeisen, müssen sie in das vom Netzwerk benötigte Format konvertiert werden. Dies wird als Vorbereiten von Daten für das Netzwerk bezeichnet. Es besteht im Allgemeinen darin, eine mehrdimensionale Eingabe in einen eindimensionalen Vektor umzuwandeln und die Datenpunkte zu normalisieren.

Eingangsvektor umformen

Die Bilder in unserem Datensatz bestehen aus 28 x 28 Pixel. Dies muss in einen eindimensionalen Vektor der Größe 28 * 28 = 784 umgewandelt werden, um ihn in unser Netzwerk einzuspeisen. Wir tun dies, indem wir die anrufenreshape Methode auf dem Vektor.

X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)

Jetzt besteht unser Trainingsvektor aus 60000 Datenpunkten, die jeweils aus einem eindimensionalen Vektor der Größe 784 bestehen. In ähnlicher Weise besteht unser Testvektor aus 10000 Datenpunkten eines eindimensionalen Vektors der Größe 784.

Daten normalisieren

Die Daten, die der Eingabevektor enthält, haben derzeit einen diskreten Wert zwischen 0 und 255 - die Graustufen. Das Normalisieren dieser Pixelwerte zwischen 0 und 1 hilft, das Training zu beschleunigen. Da wir einen stochastischen Gradientenabstieg verwenden, hilft die Normalisierung der Daten auch dabei, die Wahrscheinlichkeit zu verringern, dass sie in lokalen Optima stecken bleiben.

Um die Daten zu normalisieren, stellen wir sie als Float-Typ dar und teilen sie durch 255, wie im folgenden Code-Snippet gezeigt -

X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255

Schauen wir uns nun an, wie die normalisierten Daten aussehen.

Untersuchen normalisierter Daten

Um die normalisierten Daten anzuzeigen, rufen wir die hier gezeigte Histogrammfunktion auf -

plot.hist(X_train[0])
plot.title("Digit: {}".format(y_train[0]))

Hier zeichnen wir das Histogramm des ersten Elements der X_trainVektor. Wir drucken auch die durch diesen Datenpunkt dargestellte Ziffer. Die Ausgabe des Ausführens des obigen Codes wird hier gezeigt -

Sie werden eine dicke Punktdichte mit einem Wert nahe Null bemerken. Dies sind die schwarzen Punkte im Bild, die offensichtlich den Hauptteil des Bildes ausmachen. Die restlichen Graustufenpunkte, die nahe an der weißen Farbe liegen, repräsentieren die Ziffer. Sie können die Pixelverteilung für eine andere Ziffer überprüfen. Der folgende Code druckt das Histogramm einer Ziffer mit dem Index 2 im Trainingsdatensatz.

plot.hist(X_train[2])
plot.title("Digit: {}".format(y_train[2])

Die Ausgabe des Ausführens des obigen Codes wird unten gezeigt -

Wenn Sie die beiden obigen Abbildungen vergleichen, werden Sie feststellen, dass die Verteilung der weißen Pixel in zwei Bildern unterschiedlich ist, was auf eine Darstellung einer anderen Ziffer hinweist - "5" und "4" in den beiden obigen Bildern.

Als nächstes werden wir die Verteilung der Daten in unserem vollständigen Trainingsdatensatz untersuchen.

Untersuchen der Datenverteilung

Bevor wir unser Modell für maschinelles Lernen in unserem Datensatz trainieren, sollten wir die Verteilung der eindeutigen Ziffern in unserem Datensatz kennen. Unsere Bilder repräsentieren 10 verschiedene Ziffern im Bereich von 0 bis 9. Wir möchten die Anzahl der Ziffern 0, 1 usw. in unserem Datensatz wissen. Wir können diese Informationen über dieunique Methode von Numpy.

Verwenden Sie den folgenden Befehl, um die Anzahl der eindeutigen Werte und die Anzahl der Vorkommen jedes einzelnen zu drucken

print(np.unique(y_train, return_counts=True))

Wenn Sie den obigen Befehl ausführen, wird die folgende Ausgabe angezeigt:

(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([5923, 6742, 5958, 6131, 5842, 5421, 5918, 6265, 5851, 5949]))

Es zeigt, dass es 10 verschiedene Werte gibt - 0 bis 9. Es gibt 5923 Vorkommen von Ziffer 0, 6742 Vorkommen von Ziffer 1 und so weiter. Der Screenshot der Ausgabe wird hier gezeigt -

Als letzten Schritt bei der Datenaufbereitung müssen wir unsere Daten verschlüsseln.

Daten codieren

Wir haben zehn Kategorien in unserem Datensatz. Wir werden daher unsere Ausgabe in diesen zehn Kategorien mit One-Hot-Codierung codieren. Wir verwenden die to_categorial-Methode von Numpy-Dienstprogrammen, um die Codierung durchzuführen. Nachdem die Ausgabedaten codiert wurden, würde jeder Datenpunkt in einen eindimensionalen Vektor der Größe 10 konvertiert. Beispielsweise wird die Ziffer 5 nun als [0,0,0,0,0,1,0,0,0 "dargestellt , 0].

Codieren Sie die Daten mit dem folgenden Code:

n_classes = 10
Y_train = np_utils.to_categorical(y_train, n_classes)

Sie können das Ergebnis der Codierung überprüfen, indem Sie die ersten 5 Elemente des kategorisierten Y_train-Vektors drucken.

Verwenden Sie den folgenden Code, um die ersten 5 Vektoren zu drucken -

for i in range(5):
   print (Y_train[i])

Sie sehen die folgende Ausgabe -

[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]

Das erste Element repräsentiert die Ziffer 5, das zweite die Ziffer 0 und so weiter.

Schließlich müssen Sie auch die Testdaten kategorisieren, was mit der folgenden Anweisung erfolgt:

Y_test = np_utils.to_categorical(y_test, n_classes)

Zu diesem Zeitpunkt sind Ihre Daten vollständig für die Einspeisung in das Netzwerk vorbereitet.

Als nächstes kommt der wichtigste Teil und das ist das Training unseres Netzwerkmodells.

Das Modelltraining wird in einem einzigen Methodenaufruf namens fit durchgeführt, der nur wenige Parameter benötigt, wie im folgenden Code dargestellt.

history = model.fit(X_train, Y_train,
   batch_size=128, epochs=20,
   verbose=2,
   validation_data=(X_test, Y_test)))

Die ersten beiden Parameter der Anpassungsmethode geben die Merkmale und die Ausgabe des Trainingsdatensatzes an.

Das epochsist auf 20 eingestellt; Wir gehen davon aus, dass das Training in maximal 20 Epochen konvergiert - den Iterationen. Das trainierte Modell wird anhand der Testdaten validiert, wie im letzten Parameter angegeben.

Die Teilausgabe der Ausführung des obigen Befehls wird hier angezeigt -

Train on 60000 samples, validate on 10000 samples
Epoch 1/20
- 9s - loss: 0.2488 - acc: 0.9252 - val_loss: 0.1059 - val_acc: 0.9665
Epoch 2/20
- 9s - loss: 0.1004 - acc: 0.9688 - val_loss: 0.0850 - val_acc: 0.9715
Epoch 3/20
- 9s - loss: 0.0723 - acc: 0.9773 - val_loss: 0.0717 - val_acc: 0.9765
Epoch 4/20
- 9s - loss: 0.0532 - acc: 0.9826 - val_loss: 0.0665 - val_acc: 0.9795
Epoch 5/20
- 9s - loss: 0.0457 - acc: 0.9856 - val_loss: 0.0695 - val_acc: 0.9792

Der Screenshot der Ausgabe dient unten als Kurzreferenz -

Wenn das Modell nun anhand unserer Trainingsdaten trainiert wird, werden wir seine Leistung bewerten.

Um die Modellleistung zu bewerten, rufen wir an evaluate Methode wie folgt -

loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)

Um die Modellleistung zu bewerten, rufen wir an evaluate Methode wie folgt -

loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)

Wir werden den Verlust und die Genauigkeit anhand der folgenden zwei Aussagen drucken:

print("Test Loss", loss_and_metrics[0])
print("Test Accuracy", loss_and_metrics[1])

Wenn Sie die obigen Anweisungen ausführen, wird die folgende Ausgabe angezeigt:

Test Loss 0.08041584826191042
Test Accuracy 0.9837

Dies zeigt eine Testgenauigkeit von 98%, die für uns akzeptabel sein sollte. Was es für uns bedeutet, dass in 2% der Fälle die handschriftlichen Ziffern nicht korrekt klassifiziert werden. Wir werden auch Genauigkeits- und Verlustmetriken zeichnen, um zu sehen, wie sich das Modell auf die Testdaten auswirkt.

Zeichnen von Genauigkeitsmetriken

Wir verwenden die aufgezeichneten historywährend unseres Trainings, um ein Diagramm der Genauigkeitsmetriken zu erhalten. Der folgende Code zeigt die Genauigkeit für jede Epoche. Wir erfassen die Genauigkeit der Trainingsdaten ("acc") und die Genauigkeit der Validierungsdaten ("val_acc") zum Plotten.

plot.subplot(2,1,1)
plot.plot(history.history['acc'])
plot.plot(history.history['val_acc'])
plot.title('model accuracy')
plot.ylabel('accuracy')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='lower right')

Das Ausgabediagramm ist unten dargestellt -

Wie Sie im Diagramm sehen können, steigt die Genauigkeit in den ersten beiden Epochen schnell an, was darauf hinweist, dass das Netzwerk schnell lernt. Danach flacht die Kurve ab, was darauf hinweist, dass nicht zu viele Epochen erforderlich sind, um das Modell weiter zu trainieren. Wenn sich die Genauigkeit der Trainingsdaten („acc“) weiter verbessert, während sich die Genauigkeit der Validierungsdaten („val_acc“) verschlechtert, tritt im Allgemeinen eine Überanpassung auf. Es zeigt an, dass das Modell beginnt, die Daten zu speichern.

Wir werden auch die Verlustmetriken zeichnen, um die Leistung unseres Modells zu überprüfen.

Verlustmetriken zeichnen

Auch hier zeichnen wir den Verlust sowohl für die Trainingsdaten („Verlust“) als auch für die Testdaten („val_loss“) auf. Dies geschieht mit dem folgenden Code:

plot.subplot(2,1,2)
plot.plot(history.history['loss'])
plot.plot(history.history['val_loss'])
plot.title('model loss')
plot.ylabel('loss')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='upper right')

Die Ausgabe dieses Codes wird unten gezeigt -

Wie Sie im Diagramm sehen können, nimmt der Verlust des Trainingssatzes in den ersten beiden Epochen schnell ab. Für den Testsatz nimmt der Verlust nicht mit der gleichen Geschwindigkeit ab wie für den Trainingssatz, sondern bleibt für mehrere Epochen nahezu flach. Dies bedeutet, dass unser Modell gut auf unsichtbare Daten verallgemeinert werden kann.

Jetzt werden wir unser trainiertes Modell verwenden, um die Ziffern in unseren Testdaten vorherzusagen.

Die Ziffern in unsichtbaren Daten vorherzusagen ist sehr einfach. Sie müssen nur die anrufenpredict_classes Methode der model indem Sie es an einen Vektor übergeben, der aus Ihren unbekannten Datenpunkten besteht.

predictions = model.predict_classes(X_test)

Der Methodenaufruf gibt die Vorhersagen in einem Vektor zurück, der auf Nullen und Einsen gegen die tatsächlichen Werte getestet werden kann. Dies geschieht mit den folgenden zwei Anweisungen:

correct_predictions = np.nonzero(predictions == y_test)[0]
incorrect_predictions = np.nonzero(predictions != y_test)[0]

Schließlich werden wir die Anzahl der richtigen und falschen Vorhersagen mit den folgenden zwei Programmanweisungen drucken:

print(len(correct_predictions)," classified correctly")
print(len(incorrect_predictions)," classified incorrectly")

Wenn Sie den Code ausführen, erhalten Sie die folgende Ausgabe:

9837 classified correctly
163 classified incorrectly

Nachdem Sie das Modell zufriedenstellend trainiert haben, werden wir es für die zukünftige Verwendung aufbewahren.

Wir speichern das trainierte Modell auf unserem lokalen Laufwerk im Ordner models in unserem aktuellen Arbeitsverzeichnis. Führen Sie den folgenden Code aus, um das Modell zu speichern:

directory = "./models/"
name = 'handwrittendigitrecognition.h5'
path = os.path.join(save_dir, name)
model.save(path)
print('Saved trained model at %s ' % path)

Die Ausgabe nach dem Ausführen des Codes wird unten gezeigt -

Nachdem Sie ein trainiertes Modell gespeichert haben, können Sie es später zur Verarbeitung Ihrer unbekannten Daten verwenden.

Um die unsichtbaren Daten vorherzusagen, müssen Sie zuerst das trainierte Modell in den Speicher laden. Dies erfolgt mit dem folgenden Befehl:

model = load_model ('./models/handwrittendigitrecognition.h5')

Beachten Sie, dass wir einfach die .h5-Datei in den Speicher laden. Dadurch wird das gesamte neuronale Netzwerk im Speicher zusammen mit den jeder Schicht zugewiesenen Gewichten eingerichtet.

Um nun Ihre Vorhersagen für unsichtbare Daten zu treffen, laden Sie die Daten, lassen Sie es ein oder mehrere Elemente sein, in den Speicher. Verarbeiten Sie die Daten so, dass sie den Eingabeanforderungen unseres Modells entsprechen, wie Sie es bei Ihren Trainings- und Testdaten oben getan haben. Geben Sie es nach der Vorverarbeitung an Ihr Netzwerk weiter. Das Modell gibt seine Vorhersage aus.

Keras bietet eine High-Level-API zum Erstellen eines tiefen neuronalen Netzwerks. In diesem Tutorial haben Sie gelernt, ein tiefes neuronales Netzwerk zu erstellen, das darauf trainiert wurde, die Ziffern in handgeschriebenem Text zu finden. Zu diesem Zweck wurde ein mehrschichtiges Netzwerk erstellt. Mit Keras können Sie auf jeder Ebene eine Aktivierungsfunktion Ihrer Wahl definieren. Unter Verwendung des Gradientenabstiegs wurde das Netzwerk anhand der Trainingsdaten trainiert. Die Genauigkeit des trainierten Netzwerks bei der Vorhersage der unsichtbaren Daten wurde an den Testdaten getestet. Sie haben gelernt, die Genauigkeits- und Fehlermetriken zu zeichnen. Nachdem das Netzwerk vollständig trainiert wurde, haben Sie das Netzwerkmodell für die zukünftige Verwendung gespeichert.