LISP - Zahlen
Common Lisp definiert verschiedene Arten von Zahlen. Dasnumber Der Datentyp enthält verschiedene Arten von Nummern, die von LISP unterstützt werden.
Die von LISP unterstützten Nummerntypen sind -
- Integers
- Ratios
- Gleitkommazahlen
- Komplexe Zahlen
Das folgende Diagramm zeigt die Zahlenhierarchie und verschiedene numerische Datentypen, die in LISP verfügbar sind -
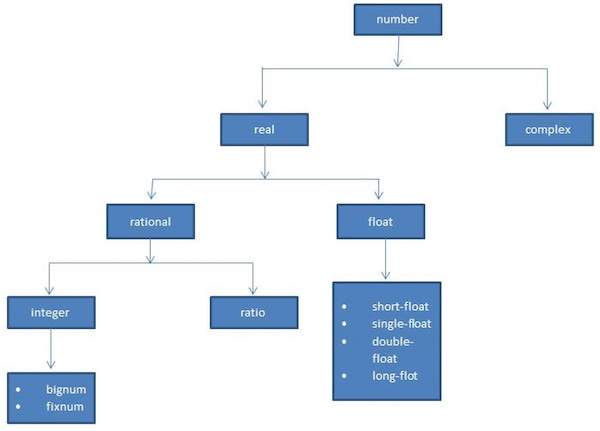
Verschiedene numerische Typen in LISP
In der folgenden Tabelle werden verschiedene in LISP verfügbare Nummerntypdaten beschrieben.
| Sr.Nr. | Datentyp & Beschreibung |
|---|---|
| 1 | fixnum Dieser Datentyp stellt Ganzzahlen dar, die nicht zu groß sind und meist im Bereich von -215 bis 215-1 liegen (er ist maschinenabhängig). |
| 2 | bignum Dies sind sehr große Zahlen, deren Größe durch die für LISP zugewiesene Speichermenge begrenzt ist. Es handelt sich nicht um feste Zahlen. |
| 3 | ratio Stellt das Verhältnis zweier Zahlen in der Zähler / Nenner-Form dar. Die / -Funktion erzeugt das Ergebnis immer in Verhältnissen, wenn ihre Argumente ganze Zahlen sind. |
| 4 | float Es repräsentiert nicht ganzzahlige Zahlen. Es gibt vier Float-Datentypen mit zunehmender Genauigkeit. |
| 5 | complex Es stellt komplexe Zahlen dar, die mit #c bezeichnet sind. Der Realteil und der Imaginärteil können entweder rationale oder Gleitkommazahlen sein. |
Beispiel
Erstellen Sie eine neue Quellcodedatei mit dem Namen main.lisp und geben Sie den folgenden Code ein.
(write (/ 1 2))
(terpri)
(write ( + (/ 1 2) (/ 3 4)))
(terpri)
(write ( + #c( 1 2) #c( 3 -4)))Wenn Sie den Code ausführen, wird das folgende Ergebnis zurückgegeben:
1/2
5/4
#C(4 -2)Zahlenfunktionen
In der folgenden Tabelle werden einige häufig verwendete numerische Funktionen beschrieben.
| Sr.Nr. | Bedienungsanleitung |
|---|---|
| 1 | +, -, *, / Entsprechende arithmetische Operationen |
| 2 | sin, cos, tan, acos, asin, atan Jeweils trigonometrische Funktionen. |
| 3 | sinh, cosh, tanh, acosh, asinh, atanh Entsprechende hyperbolische Funktionen. |
| 4 | exp Exponentiationsfunktion. Berechnet e x |
| 5 | expt Exponentiationsfunktion, nimmt Basis und Macht beide. |
| 6 | sqrt Es berechnet die Quadratwurzel einer Zahl. |
| 7 | log Logarithmische Funktion. Wenn ein Parameter angegeben wird, berechnet er seinen natürlichen Logarithmus, andernfalls wird der zweite Parameter als Basis verwendet. |
| 8 | conjugate Es berechnet das komplexe Konjugat einer Zahl. Bei einer reellen Zahl wird die Zahl selbst zurückgegeben. |
| 9 | abs Es gibt den absoluten Wert (oder die Größe) einer Zahl zurück. |
| 10 | gcd Es berechnet den größten gemeinsamen Teiler der angegebenen Zahlen. |
| 11 | lcm Es berechnet das kleinste gemeinsame Vielfache der angegebenen Zahlen. |
| 12 | isqrt Es gibt die größte ganze Zahl, die kleiner oder gleich der exakten Quadratwurzel einer gegebenen natürlichen Zahl ist. |
| 13 | floor, ceiling, truncate, round Alle diese Funktionen verwenden zwei Argumente als Zahl und geben den Quotienten zurück. floor Gibt die größte Ganzzahl zurück, die nicht größer als das Verhältnis ist. ceiling wählt die kleinere ganze Zahl, die größer als das Verhältnis ist, truncate wählt die ganze Zahl mit dem gleichen Vorzeichen wie das Verhältnis mit dem größten absoluten Wert, der kleiner als der absolute Wert des Verhältnisses ist, und round wählt eine Ganzzahl, die dem Verhältnis am nächsten kommt. |
| 14 | ffloor, fceiling, ftruncate, fround Funktioniert wie oben, gibt jedoch den Quotienten als Gleitkommazahl zurück. |
| 15 | mod, rem Gibt den Rest in einer Divisionsoperation zurück. |
| 16 | float Konvertiert eine reelle Zahl in eine Gleitkommazahl. |
| 17 | rational, rationalize Wandelt eine reelle Zahl in eine rationale Zahl um. |
| 18 | numerator, denominator Gibt die jeweiligen Teile einer rationalen Zahl zurück. |
| 19 | realpart, imagpart Gibt den Real- und Imaginärteil einer komplexen Zahl zurück. |
Beispiel
Erstellen Sie eine neue Quellcodedatei mit dem Namen main.lisp und geben Sie den folgenden Code ein.
(write (/ 45 78))
(terpri)
(write (floor 45 78))
(terpri)
(write (/ 3456 75))
(terpri)
(write (floor 3456 75))
(terpri)
(write (ceiling 3456 75))
(terpri)
(write (truncate 3456 75))
(terpri)
(write (round 3456 75))
(terpri)
(write (ffloor 3456 75))
(terpri)
(write (fceiling 3456 75))
(terpri)
(write (ftruncate 3456 75))
(terpri)
(write (fround 3456 75))
(terpri)
(write (mod 3456 75))
(terpri)
(setq c (complex 6 7))
(write c)
(terpri)
(write (complex 5 -9))
(terpri)
(write (realpart c))
(terpri)
(write (imagpart c))Wenn Sie den Code ausführen, wird das folgende Ergebnis zurückgegeben:
15/26
0
1152/25
46
47
46
46
46.0
47.0
46.0
46.0
6
#C(6 7)
#C(5 -9)
6
7