LISP - Baum

Sie können Baumdatenstrukturen aus Cons-Zellen als Listen von Listen erstellen.

Um Baumstrukturen zu implementieren, müssen Sie Funktionen entwerfen, die die Nachteile-Zellen in einer bestimmten Reihenfolge durchlaufen, z. B. in der Reihenfolge vor, in der Reihenfolge und nach der Reihenfolge für Binärbäume.

Baum als Listenliste

Betrachten wir eine Baumstruktur aus Cons-Zellen, die die folgende Liste von Listen bilden:

((1 2) (3 4) (5 6)).

Diagrammatisch könnte es ausgedrückt werden als -

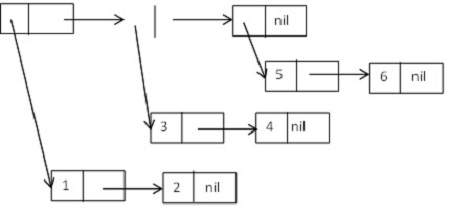
Baumfunktionen in LISP

Obwohl Sie meistens Ihre eigenen Baumfunktionen entsprechend Ihren spezifischen Anforderungen schreiben müssen, bietet LISP einige Baumfunktionen, die Sie verwenden können.

Abgesehen von allen Listenfunktionen funktionieren die folgenden Funktionen insbesondere für Baumstrukturen:

Sr.Nr.	Bedienungsanleitung
1	copy-tree x & optional vecp Es wird eine Kopie des Baums der Nachteilezellen x zurückgegeben. Es kopiert rekursiv sowohl die Auto- als auch die CDR-Richtung. Wenn x keine Nachteilezelle ist, gibt die Funktion x einfach unverändert zurück. Wenn das optionale vecp-Argument wahr ist, kopiert diese Funktion sowohl Vektoren (rekursiv) als auch Nachteile-Zellen.
2	tree-equal xy & key: test: test-not: key Es vergleicht zwei Bäume von Nachteilezellen. Wenn x und y beide Nachteile sind, werden ihre Autos und CDs rekursiv verglichen. Wenn weder x noch y eine Nachteilezelle sind, werden sie nach Gleichung oder gemäß dem angegebenen Test verglichen. Die Funktion: key wird, falls angegeben, auf die Elemente beider Bäume angewendet.
3	subst neuer alter Baum & Schlüssel: Test: Test-nicht: Schlüssel Es ersetzt das Auftreten eines bestimmten alten Elements durch ein neues Element im Baum , der ein Baum von Nachteilezellen ist.
4	nsubst neuer alter Baum & Schlüssel: Test: Test-nicht: Schlüssel Es funktioniert genauso wie subst, zerstört jedoch den ursprünglichen Baum.
5	sublis Alist Tree & Key: Test: Test-Not: Key Es funktioniert wie subst, außer dass eine Zuordnungsliste mit alten und neuen Paaren erstellt wird. Jedes Element des Baums (nach Anwendung der Funktion: key, falls vorhanden) wird mit den Autos von alist verglichen. Wenn es übereinstimmt, wird es durch die entsprechende CDR ersetzt.
6	nsublis Alist Tree & Key: Test: Test-Not: Key Es funktioniert genauso wie Sublis, ist jedoch eine destruktive Version.

Beispiel 1

Erstellen Sie eine neue Quellcodedatei mit dem Namen main.lisp und geben Sie den folgenden Code ein.

(setq lst (list '(1 2) '(3 4) '(5 6)))
(setq mylst (copy-list lst))
(setq tr (copy-tree lst))

(write lst)
(terpri)
(write mylst)
(terpri)
(write tr)

Wenn Sie den Code ausführen, wird das folgende Ergebnis zurückgegeben:

((1 2) (3 4) (5 6))
((1 2) (3 4) (5 6))
((1 2) (3 4) (5 6))

Beispiel 2

Erstellen Sie eine neue Quellcodedatei mit dem Namen main.lisp und geben Sie den folgenden Code ein.

(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9)))))
(write tr)
(setq trs (subst 7 1 tr))
(terpri)
(write trs)

Wenn Sie den Code ausführen, wird das folgende Ergebnis zurückgegeben:

((1 2 (3 4 5) ((7 8) (7 8 9))))
((7 2 (3 4 5) ((7 8) (7 8 9))))

Bauen Sie Ihren eigenen Baum

Versuchen wir, mithilfe der in LISP verfügbaren Listenfunktionen einen eigenen Baum zu erstellen.

Lassen Sie uns zunächst einen neuen Knoten erstellen, der einige Daten enthält

(defun make-tree (item)
   "it creates a new node with item."
   (cons (cons item nil) nil)
)

Als nächstes fügen wir dem Baum einen untergeordneten Knoten hinzu - es werden zwei Baumknoten benötigt und der zweite Baum als untergeordnetes Element des ersten Baums hinzugefügt.

(defun add-child (tree child)
   (setf (car tree) (append (car tree) child))
   tree)

Diese Funktion gibt dem ersten Kind einen bestimmten Baum zurück - sie nimmt einen Baumknoten und gibt das erste Kind dieses Knotens zurück, oder null, wenn dieser Knoten keinen untergeordneten Knoten hat.

(defun first-child (tree)
   (if (null tree)
      nil
      (cdr (car tree))
   )
)

Diese Funktion gibt das nächste Geschwister eines bestimmten Knotens zurück - sie verwendet einen Baumknoten als Argument und gibt einen Verweis auf den nächsten Geschwisterknoten oder null zurück, wenn der Knoten keinen hat.

(defun next-sibling (tree)
   (cdr tree)
)

Zuletzt benötigen wir eine Funktion, um die Informationen in einem Knoten zurückzugeben -

(defun data (tree)
   (car (car tree))
)

Beispiel

In diesem Beispiel werden die oben genannten Funktionen verwendet -

Erstellen Sie eine neue Quellcodedatei mit dem Namen main.lisp und geben Sie den folgenden Code ein.

(defun make-tree (item)
   "it creates a new node with item."
   (cons (cons item nil) nil)
)
(defun first-child (tree)
   (if (null tree)
      nil
      (cdr (car tree))
   )
)

(defun next-sibling (tree)
   (cdr tree)
)
(defun data (tree)
   (car (car tree))
)
(defun add-child (tree child)
   (setf (car tree) (append (car tree) child))
   tree
)

(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9)))))
(setq mytree (make-tree 10))

(write (data mytree))
(terpri)
(write (first-child tr))
(terpri)
(setq newtree (add-child tr mytree))
(terpri)
(write newtree)

Wenn Sie den Code ausführen, wird das folgende Ergebnis zurückgegeben:

10
(2 (3 4 5) ((7 8) (7 8 9)))

((1 2 (3 4 5) ((7 8) (7 8 9)) (10)))