Plotly - Box Plot Geigenplot und Konturplot

Dieses Kapitel konzentriert sich auf das Detailverständnis über verschiedene Diagramme, einschließlich Box-Diagramm, Geigen-Diagramm, Kontur-Diagramm und Köcher-Diagramm. Zunächst beginnen wir mit dem Box Plot.

Box-Plot

Ein Box-Plot zeigt eine Zusammenfassung eines Datensatzes an, der das Minimum enthält. first quartile, median, third quartile, und maximum. In einem Boxplot zeichnen wir eine Box vom ersten bis zum dritten Quartil. Eine vertikale Linie verläuft im Median durch das Feld. Die Linien, die sich vertikal von den Feldern erstrecken und die Variabilität außerhalb des oberen und unteren Quartils anzeigen, werden als Whisker bezeichnet. Daher wird Box-Plot auch als Box und bezeichnetwhisker plot. Die Whisker gehen von jedem Quartil zum Minimum oder Maximum.

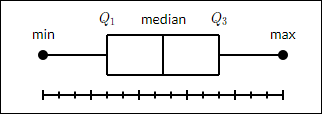
Um ein Box-Diagramm zu zeichnen, müssen wir verwenden go.Box()Funktion. Die Datenreihen können dem Parameter x oder y zugeordnet werden. Dementsprechend wird das Box-Diagramm horizontal oder vertikal gezeichnet. Im folgenden Beispiel werden die Verkaufszahlen eines bestimmten Unternehmens in seinen verschiedenen Niederlassungen in ein horizontales Boxplot umgewandelt. Es zeigt den Median des Minimal- und Maximalwerts.

trace1 = go.Box(y = [1140,1460,489,594,502,508,370,200])
data = [trace1]
fig = go.Figure(data)
iplot(fig)

Die Ausgabe desselben wird wie folgt sein:

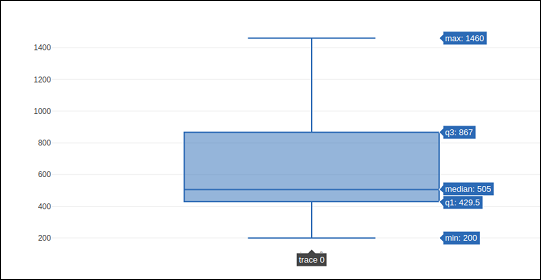
Das go.Box()Der Funktion können verschiedene andere Parameter zugewiesen werden, um das Erscheinungsbild und Verhalten des Boxplots zu steuern. Ein solcher ist der Boxmean-Parameter.

Das boxmeanDer Parameter ist standardmäßig auf true gesetzt. Infolgedessen wird der Mittelwert der zugrunde liegenden Verteilung der Boxen als gestrichelte Linie innerhalb der Boxen gezeichnet. Wenn sd eingestellt ist, wird auch die Standardabweichung der Verteilung gezeichnet.

Das boxpoints Parameter ist standardmäßig gleich "outliers". Es werden nur die außerhalb der Whisker liegenden Probenpunkte angezeigt. Bei" vermuteten Ausreißern "werden die Ausreißerpunkte angezeigt und Punkte, die entweder kleiner als 4" Q1-3 "Q3 oder größer als 4" Q3-3 "Q1 sind, werden hervorgehoben. False ", nur die Kästchen werden ohne Beispielpunkte angezeigt.

Im folgenden Beispiel wird die box trace wird mit Standardabweichung und Ausreißerpunkten gezeichnet.

trc = go.Box(
   y = [
      0.75, 5.25, 5.5, 6, 6.2, 6.6, 6.80, 7.0, 7.2, 7.5, 7.5, 7.75, 8.15,
      8.15, 8.65, 8.93, 9.2, 9.5, 10, 10.25, 11.5, 12, 16, 20.90, 22.3, 23.25
   ],
   boxpoints = 'suspectedoutliers', boxmean = 'sd'
)
data = [trc]
fig = go.Figure(data)
iplot(fig)

Die Ausgabe derselben ist unten angegeben -

Geigenplot

Violin-Plots ähneln Box-Plots, zeigen jedoch auch die Wahrscheinlichkeitsdichte der Daten bei verschiedenen Werten. Violin-Plots enthalten eine Markierung für den Median der Daten und ein Feld, das den Interquartilbereich angibt, wie in Standard-Box-Plots. Diesem Boxplot ist eine Schätzung der Kerneldichte überlagert. Geigenplots werden wie Box-Plots verwendet, um den Vergleich einer variablen Verteilung (oder Stichprobenverteilung) über verschiedene "Kategorien" darzustellen.

Eine Geigenhandlung ist informativer als eine einfache Boxhandlung. Während in einem Box-Plot nur zusammenfassende Statistiken wie Mittelwert / Median und Interquartil angezeigt werden, zeigt das Geigen-Plot diefull distribution of the data.

Das Violin-Trace-Objekt wird von zurückgegeben go.Violin() Funktion in graph_objectsModul. Um das zugrunde liegende Box-Diagramm anzuzeigen, wird dieboxplot_visibleAttribut ist auf True gesetzt. Ebenso durch Einstellenmeanline_visible Eigenschaft auf wahr, wird innerhalb der Geigen eine Linie angezeigt, die dem Mittelwert der Probe entspricht.

Das folgende Beispiel zeigt, wie der Violin-Plot mithilfe der Plotly-Funktionalität angezeigt wird.

import numpy as np
np.random.seed(10)
c1 = np.random.normal(100, 10, 200)
c2 = np.random.normal(80, 30, 200)
trace1 = go.Violin(y = c1, meanline_visible = True)
trace2 = go.Violin(y = c2, box_visible = True)
data = [trace1, trace2]
fig = go.Figure(data = data)
iplot(fig)

Die Ausgabe ist wie folgt -

Konturdiagramm

Ein 2D-Konturdiagramm zeigt die Konturlinien eines numerischen 2D-Arrays z, dh interpolierte Linien von isovaluesvon z. Eine Konturlinie einer Funktion aus zwei Variablen ist eine Kurve, entlang der die Funktion einen konstanten Wert hat, so dass die Kurve gleichwertige Punkte verbindet.

Ein Konturdiagramm ist geeignet, wenn Sie sehen möchten, wie sich ein Wert Z in Abhängigkeit von zwei Eingaben ändert. X und Y so dass Z = f(X,Y). Eine Konturlinie oder Isolinie einer Funktion zweier Variablen ist eine Kurve, entlang der die Funktion einen konstanten Wert hat.

Die unabhängigen Variablen x und y sind normalerweise auf ein reguläres Gitter namens Meshgrid beschränkt. Das numpy.meshgrid erstellt ein rechteckiges Gitter aus einem Array von x-Werten und einem Array von y-Werten.

Erstellen wir zunächst Datenwerte für x, y und z mit linspace()Funktion aus der Numpy-Bibliothek. Wir schaffen einemeshgrid aus x- und y-Werten und erhalten Sie ein z-Array bestehend aus Quadratwurzel von x2+y2

Wir haben go.Contour() Funktion in graph_objects Modul, das x nimmt,y und zAttribute. Das folgende Code-Snippet zeigt das Konturdiagramm von x an.y und z Werte wie oben berechnet.

import numpy as np
xlist = np.linspace(-3.0, 3.0, 100)
ylist = np.linspace(-3.0, 3.0, 100)
X, Y = np.meshgrid(xlist, ylist)
Z = np.sqrt(X**2 + Y**2)
trace = go.Contour(x = xlist, y = ylist, z = Z)
data = [trace]
fig = go.Figure(data)
iplot(fig)

Die Ausgabe ist wie folgt -

Das Konturdiagramm kann durch einen oder mehrere der folgenden Parameter angepasst werden:

• Transpose (boolean) - Transponiert die z-Daten.

Wenn xtype (oder ytype) gleich "Array", x / y-Koordinaten sind durch "x" / "y" gegeben. Wenn "skaliert", werden x-Koordinaten durch "x0" und "dx".

• Das connectgaps Der Parameter bestimmt, ob Lücken in den z-Daten ausgefüllt werden.

• Standardwert von ncontoursParameter ist 15. Die tatsächliche Anzahl der Konturen wird automatisch so gewählt, dass sie kleiner oder gleich dem Wert von "ncontours" ist. Wirkt sich nur aus, wenn "Autokontur" "Wahr" ist.

Der Konturtyp ist standardmäßig: "levels"Die Daten werden also als Konturdiagramm mit mehreren Ebenen dargestellt. Wenn constrainwerden die Daten als Einschränkungen dargestellt, wobei der ungültige Bereich gemäß den Angaben in schattiert ist operation und value Parameter.

showlines - Legt fest, ob die Konturlinien gezeichnet werden.

zauto ist True Standardmäßig und bestimmt, ob die Farbdomäne in Bezug auf die Eingabedaten (hier in "z") oder die in "festgelegten Grenzen" berechnet wirdzmin`und`zmax`Standardmäßig`False`wenn` zmin` und` zmax` vom Benutzer eingestellt werden.

Köcherplot

Köcherplot ist auch bekannt als velocity plot. Es zeigt Geschwindigkeitsvektoren als Pfeile mit Komponenten an (u,v) an den Punkten (x, y). Um einen Köcherplot zu zeichnen, werden wir verwendencreate_quiver() Funktion definiert in figure_factory Modul in Plotly.

Die Python-API von Plotly enthält ein Figure Factory-Modul, das viele Wrapper-Funktionen enthält, mit denen eindeutige Diagrammtypen erstellt werden, die noch nicht enthalten sind plotly.js, Plotlys Open-Source-Grafikbibliothek.

Die Funktion create_quiver () akzeptiert folgende Parameter:

• x - x Koordinaten der Pfeilpositionen

• y - y Koordinaten der Pfeilpositionen

• u - x Komponenten der Pfeilvektoren

• v - y Komponenten der Pfeilvektoren

• scale - Skaliert die Größe der Pfeile

• arrow_scale - Länge der Pfeilspitze.

• angle - Winkel der Pfeilspitze.

Der folgende Code rendert einen einfachen Köcherplot im Jupyter-Notizbuch -

import plotly.figure_factory as ff
import numpy as np
x,y = np.meshgrid(np.arange(-2, 2, .2), np.arange(-2, 2, .25))
z = x*np.exp(-x**2 - y**2)
v, u = np.gradient(z, .2, .2)

# Create quiver figure
fig = ff.create_quiver(x, y, u, v,
scale = .25, arrow_scale = .4,
name = 'quiver', line = dict(width = 1))
iplot(fig)

Die Ausgabe des Codes ist wie folgt: