Amplitudenmodulation
Unter den Arten von Modulationstechniken ist die Hauptklassifikation die Dauerstrichmodulation und die Pulsmodulation. Die Dauerstrichmodulationstechniken sind weiter unterteilt inAmplitude Modulation und Angle Modulation.
Eine kontinuierliche Welle läuft kontinuierlich ohne Intervalle weiter und es ist das Basisband-Nachrichtensignal, das die Informationen enthält. Diese Welle muss moduliert werden.
Gemäß der Standarddefinition "variiert die Amplitude des Trägersignals entsprechend der momentanen Amplitude des Modulationssignals." Das heißt, die Amplitude des Trägersignals, das keine Informationen enthält, ändert sich zu jedem Zeitpunkt gemäß der Amplitude des Signals, das Informationen enthält. Dies kann durch die folgenden Abbildungen gut erklärt werden.
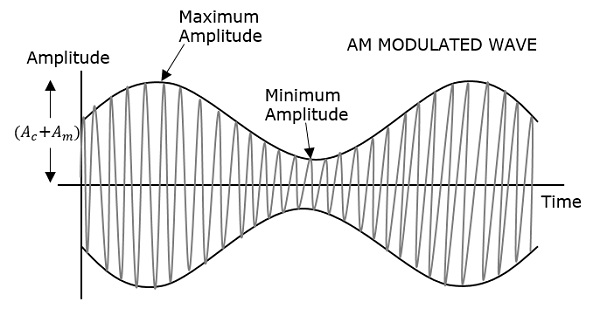
Die zuerst gezeigte Modulationswelle ist das Nachrichtensignal. Die nächste ist die Trägerwelle, die nur ein Hochfrequenzsignal ist und keine Informationen enthält. Während die letzte die resultierende modulierte Welle ist.
Es kann beobachtet werden, dass die positiven und negativen Spitzen der Trägerwelle mit einer imaginären Linie verbunden sind. Diese Linie hilft dabei, die genaue Form des Modulationssignals wiederherzustellen. Diese imaginäre Linie auf der Trägerwelle wird als bezeichnetEnvelope. Es ist dasselbe wie das Nachrichtensignal.
Mathematischer Ausdruck
Es folgt der mathematische Ausdruck für diese Wellen.
Zeitbereichsdarstellung der Wellen
Das Modulationssignal sei -
$$ m (t) = A_mcos (2 \ pi f_mt) $$
Das Trägersignal sei -
$$ c (t) = A_ccos (2 \ pi f_ct) $$
Wo Am = maximale Amplitude des Modulationssignals
Ac = maximale Amplitude des Trägersignals
Die Standardform einer amplitudenmodulierten Welle ist definiert als -
$$ S (t) = A_c [1 + K_am (t)] cos (2 \ pi f_ct) $$
$$ S (t) = A_c [1+ \ mu cos (2 \ pi f_mt)] cos (2 \ pi f_ct) $$
$$ Wobei \ mu = K_aA_m $$
Modulationsgrad
Eine Trägerwelle wird nach der Modulation, wenn der modulierte Pegel berechnet wird, als ein solcher Versuch bezeichnet als Modulation Index oder Modulation Depth. Es gibt den Modulationsgrad an, den eine Trägerwelle erfährt.
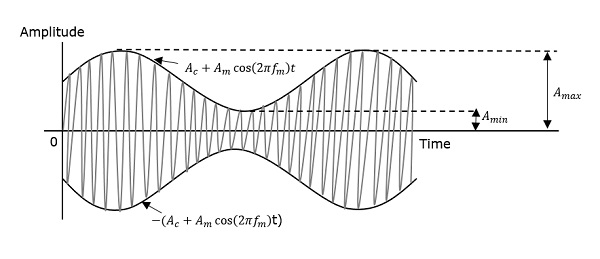
Die Maximal- und Minimalwerte der Hüllkurve der modulierten Welle werden durch A max bzw. A min dargestellt .
Versuchen wir, eine Gleichung für den Modulationsindex zu entwickeln.
$$ A_ {max} = A_c (1+ \ mu) $$
Da bei A max der Wert von cos θ 1 ist
$$ A_ {min} = A_c (1- \ mu) $$
Da bei A min der Wert von cos θ -1 ist
$$ \ frac {A_ {max}} {A_ {min}} = \ frac {1+ \ mu} {1- \ mu} $$
$$ A_ {max} - \ mu A_ {max} = A_ {min} + \ mu A_ {min} $$
$$ - \ mu (A_ {max} + A_ {min}) = A_ {min} -A_ {max} $$
$$ \ mu = \ frac {A_ {max} -A_ {min}} {A_ {max} + A_ {min}} $$
Daher wird die Gleichung für den Modulationsindex erhalten. µbezeichnet den Modulationsindex oder die Modulationstiefe. Dies wird oft in Prozent angegeben, die als bezeichnet werdenPercentage Modulation. Es ist das Ausmaß der Modulation, angegeben in Prozent, und wird mit bezeichnetm.
Für eine perfekte Modulation sollte der Wert des Modulationsindex 1 sein, was bedeutet, dass die Modulationstiefe 100% betragen sollte.
Wenn dieser Wert beispielsweise kleiner als 1 ist, dh der Modulationsindex 0,5 beträgt, sieht der modulierte Ausgang wie in der folgenden Abbildung aus. Es wird als Untermodulation bezeichnet. Eine solche Welle wird alsunder-modulated wave.
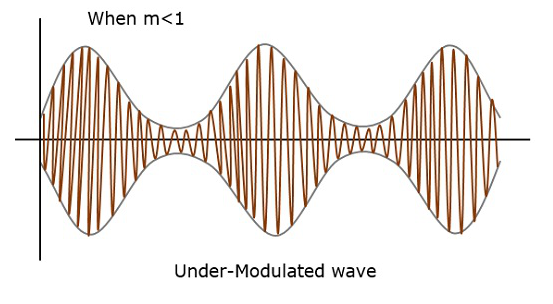
Wenn der Wert des Modulationsindex größer als 1 ist, dh 1,5 oder so, ist die Welle eine over-modulated wave. Es würde wie in der folgenden Abbildung aussehen.

Wenn der Wert des Modulationsindex zunimmt, erfährt der Träger eine 180 ° -Phasenumkehr, die zusätzliche Seitenbänder verursacht und daher die Welle verzerrt wird. Eine solche übermodulierte Welle verursacht Interferenzen, die nicht beseitigt werden können.
Bandbreite der Amplitudenmodulation
Die Bandbreite ist die Differenz zwischen der niedrigsten und der höchsten Frequenz des Signals.
Für amplitudenmodulierte Wellen ist die Bandbreite gegeben durch
$$ BW = f_ {USB} -f_ {LSB} $$
$$ (f_c + f_m) - (f_c-f_m) $$
$$ = 2f_m = 2W $$
Wo W ist die Nachrichtenbandbreite
Daher haben wir erfahren, dass die für die amplitudenmodulierte Welle erforderliche Bandbreite doppelt so hoch ist wie die Frequenz des modulierenden Signals.