Pulsmodulation
Bisher haben wir über Dauerstrichmodulation diskutiert. Jetzt ist es Zeit für diskrete Signale. DasPulse modulationTechniken, befasst sich mit diskreten Signalen. Lassen Sie uns sehen, wie ein kontinuierliches Signal in ein diskretes umgewandelt wird. Der Prozess namens Sampling hilft uns dabei.
Probenahme
Der Prozess der Umwandlung kontinuierlicher Zeitsignale in äquivalente diskrete Zeitsignale kann als bezeichnet werden Sampling. Ein bestimmter Zeitpunkt der Daten wird während des Abtastvorgangs kontinuierlich abgetastet.
Die folgende Abbildung zeigt ein zeitkontinuierliches Signal x(t) und ein abgetastetes Signal xs(t). Wannx(t) wird mit einer periodischen Impulsfolge multipliziert, dem abgetasteten Signal xs(t) erhalten wird.
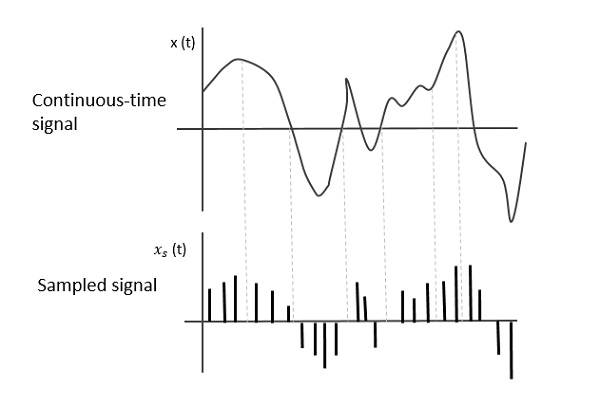
EIN sampling signal ist eine periodische Folge von Impulsen mit unit amplitude, in gleichen Zeitintervallen abgetastet Ts, die als die bezeichnet wird Sampling time. Diese Daten werden zu den Zeitpunkten übertragenTs und das Trägersignal wird zur verbleibenden Zeit übertragen.
Abtastrate
Um die Signale zu diskretisieren, sollte der Abstand zwischen den Abtastwerten festgelegt werden. Diese Lücke kann als die bezeichnet werdensampling period Ts.
$$ Sampling \: Frequenz = \ frac {1} {T_s} = f_s $$
Wo,
Ts = die Abtastzeit
fs = Abtastfrequenz oder Abtastrate
Abtasttheorem
Bei der Betrachtung der Abtastrate sollte ein wichtiger Punkt in Bezug auf die Höhe der Rate berücksichtigt werden. Dasrate of sampling sollte so sein, dass die Daten im Nachrichtensignal weder verloren gehen noch überlappen.
Das sampling theorem heißt es: „Ein Signal kann exakt wiedergegeben werden, wenn es mit der Rate abgetastet wird fs das größer oder gleich der doppelten maximalen Frequenz W ist. “
Einfacher ausgedrückt sollte die Abtastrate für die effektive Wiedergabe des Originalsignals doppelt so hoch sein wie die höchste Frequenz.
Was bedeutet,
$$ f_s \ geq 2W $$
Wo,
fs = die Abtastfrequenz
W ist die höchste Frequenz
Diese Abtastrate wird als bezeichnet Nyquist rate.
Der Abtastsatz, der auch als bezeichnet wird Nyquist theoremliefert die Theorie einer ausreichenden Abtastrate in Bezug auf die Bandbreite für die Klasse von Funktionen, die bandbegrenzt sind.
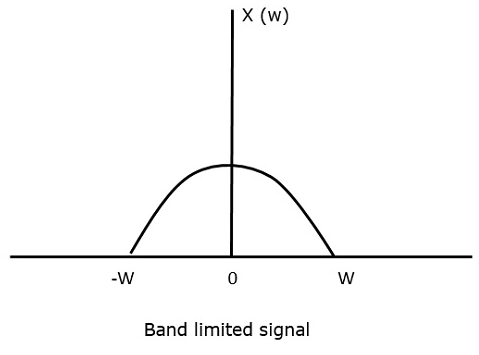
Für das zeitkontinuierliche Signal x(t)Das bandbegrenzte Signal im Frequenzbereich kann wie in der folgenden Abbildung dargestellt dargestellt werden.
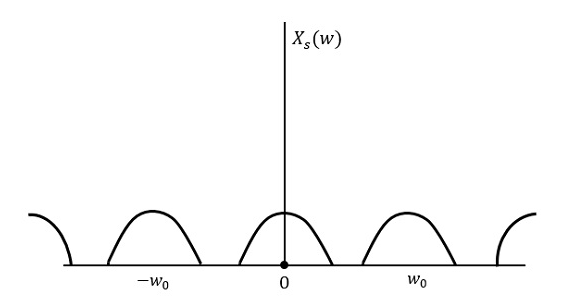
Wenn das Signal oberhalb der Nyquist-Rate abgetastet wird, kann das ursprüngliche Signal wiederhergestellt werden. Die folgende Abbildung erläutert ein Signal, wenn es im Frequenzbereich mit einer höheren Rate als 2 W abgetastet wird.
Wenn dasselbe Signal mit einer Rate von weniger als 2 W abgetastet wird, sieht das abgetastete Signal wie in der folgenden Abbildung aus.
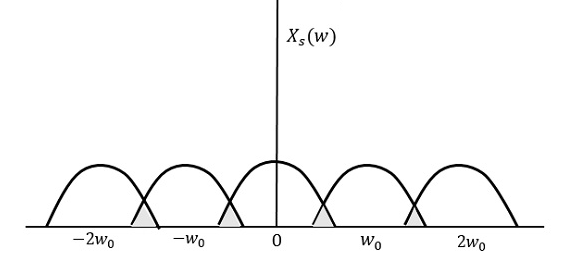
Aus dem obigen Muster können wir beobachten, dass das Überlappen von Informationen erfolgt, was zu Verwechslungen und Informationsverlust führt. Dieses unerwünschte Phänomen des Überlappens wird als bezeichnetAliasing.
Aliasing kann als "das Phänomen einer Hochfrequenzkomponente im Spektrum eines Signals bezeichnet werden, das im Spektrum seiner abgetasteten Version die Identität einer Niederfrequenzkomponente annimmt".
Daher wird die Abtastung des Signals so gewählt, dass sie mit der Nyquist-Rate erfolgt, wie im Abtasttheorem angegeben. Wenn die Abtastrate doppelt so hoch ist wie die höchste Frequenz (2 W).
Das bedeutet,
$$ f_s = 2W $$
Wo,
fs = die Abtastfrequenz
W ist die höchste Frequenz

Das Ergebnis ist wie in der obigen Abbildung gezeigt. Die Informationen werden ohne Verlust ersetzt. Daher ist dies eine gute Abtastrate.