Teoría de los autómatas - Guía rápida
Autómatas - ¿Qué es?
El término "Autómatas" se deriva de la palabra griega "αὐτόματα" que significa "autoactiva". Un autómata (Automata en plural) es un dispositivo informático autopropulsado abstracto que sigue una secuencia predeterminada de operaciones automáticamente.
Un autómata con un número finito de estados se llama Finite Automaton (FA) o Finite State Machine (FSM).
Definición formal de un autómata finito
Un autómata puede representarse mediante una tupla de 5 (Q, ∑, δ, q 0 , F), donde -
Q es un conjunto finito de estados.
∑ es un conjunto finito de símbolos, llamado alphabet del autómata.
δ es la función de transición.
q0es el estado inicial desde donde se procesa cualquier entrada (q 0 ∈ Q).
F es un conjunto de estados finales de Q (F ⊆ Q).
Terminologías relacionadas
Alfabeto
Definition - un alphabet es cualquier conjunto finito de símbolos.
Example - ∑ = {a, b, c, d} es una alphabet set donde 'a', 'b', 'c' y 'd' son symbols.
Cuerda
Definition - A string es una secuencia finita de símbolos tomados de ∑.
Example - 'cabcad' es una cadena válida en el conjunto alfabético ∑ = {a, b, c, d}
Longitud de una cuerda
Definition- Es el número de símbolos presentes en una cadena. (Denotado por|S|).
Examples -
Si S = 'cabcad', | S | = 6
Si | S | = 0, se llama empty string (Denotado por λ o ε)
Estrella de Kleene
Definition - La estrella de Kleene, ∑*, es un operador unario en un conjunto de símbolos o cadenas, ∑, que da el conjunto infinito de todas las cadenas posibles de todas las longitudes posibles en ∑ incluso λ.
Representation- ∑ * = ∑ 0 ∪ ∑ 1 ∪ ∑ 2 ∪ ……. donde ∑ p es el conjunto de todas las cadenas posibles de longitud p.
Example - Si ∑ = {a, b}, ∑ * = {λ, a, b, aa, ab, ba, bb, ……… ..}
Cierre Kleene / Plus
Definition - El conjunto ∑+ es el conjunto infinito de todas las cadenas posibles de todas las longitudes posibles sobre ∑ excluyendo λ.
Representation- ∑ + = ∑ 1 ∪ ∑ 2 ∪ ∑ 3 ∪ …….
∑ + = ∑ * - {λ}
Example- Si ∑ = {a, b}, ∑ + = {a, b, aa, ab, ba, bb, ……… ..}
Idioma
Definition- Un idioma es un subconjunto de ∑ * para algún alfabeto ∑. Puede ser finito o infinito.
Example - Si el lenguaje toma todas las cadenas posibles de longitud 2 sobre ∑ = {a, b}, entonces L = {ab, aa, ba, bb}
El autómata finito se puede clasificar en dos tipos:
- Autómata finito determinista (DFA)
- Autómata finito no determinista (NDFA / NFA)
Autómata finito determinista (DFA)
En DFA, para cada símbolo de entrada, se puede determinar el estado al que se moverá la máquina. Por lo tanto, se llamaDeterministic Automaton. Como tiene un número finito de estados, la máquina se llamaDeterministic Finite Machine o Deterministic Finite Automaton.
Definición formal de un DFA
Un DFA puede estar representado por una tupla de 5 (Q, ∑, δ, q 0 , F) donde -
Q es un conjunto finito de estados.
∑ es un conjunto finito de símbolos llamado alfabeto.
δ es la función de transición donde δ: Q × ∑ → Q
q0es el estado inicial desde donde se procesa cualquier entrada (q 0 ∈ Q).
F es un conjunto de estados finales de Q (F ⊆ Q).
Representación gráfica de un DFA
Un DFA está representado por dígrafos llamados state diagram.
- Los vértices representan los estados.
- Los arcos etiquetados con un alfabeto de entrada muestran las transiciones.
- El estado inicial se denota por un solo arco entrante vacío.
- El estado final está indicado por círculos dobles.
Ejemplo
Sea un autómata finito determinista →
- Q = {a, b, c},
- ∑ = {0, 1},
- q 0 = {a},
- F = {c} y
Función de transición δ como se muestra en la siguiente tabla -
| Estado actual | Siguiente estado para la entrada 0 | Siguiente estado para la entrada 1 |
|---|---|---|
| a | un | segundo |
| b | C | un |
| c | segundo | C |
Su representación gráfica sería la siguiente:

En NDFA, para un símbolo de entrada particular, la máquina puede moverse a cualquier combinación de estados en la máquina. En otras palabras, no se puede determinar el estado exacto al que se mueve la máquina. Por lo tanto, se llamaNon-deterministic Automaton. Como tiene un número finito de estados, la máquina se llamaNon-deterministic Finite Machine o Non-deterministic Finite Automaton.
Definición formal de un NDFA
Un NDFA se puede representar por una tupla de 5 (Q, ∑, δ, q 0 , F) donde -
Q es un conjunto finito de estados.
∑ es un conjunto finito de símbolos llamados alfabetos.
δes la función de transición donde δ: Q × ∑ → 2 Q
(Aquí se ha tomado el conjunto de potencias de Q (2 Q ) porque en el caso de NDFA, desde un estado, puede ocurrir una transición a cualquier combinación de estados Q)
q0es el estado inicial desde donde se procesa cualquier entrada (q 0 ∈ Q).
F es un conjunto de estados finales de Q (F ⊆ Q).
Representación gráfica de un NDFA: (igual que DFA)
Un NDFA está representado por dígrafos llamados diagrama de estado.
- Los vértices representan los estados.
- Los arcos etiquetados con un alfabeto de entrada muestran las transiciones.
- El estado inicial se denota por un solo arco entrante vacío.
- El estado final está indicado por círculos dobles.
Example
Sea un autómata finito no determinista →
- Q = {a, b, c}
- ∑ = {0, 1}
- q 0 = {a}
- F = {c}
La función de transición δ como se muestra a continuación:
| Estado actual | Siguiente estado para la entrada 0 | Siguiente estado para la entrada 1 |
|---|---|---|
| un | a, b | segundo |
| segundo | C | a, c |
| C | antes de Cristo | C |
Su representación gráfica sería la siguiente:
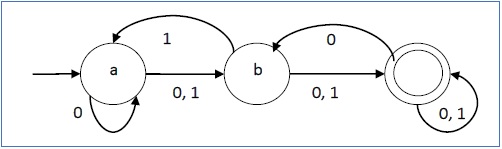
DFA frente a NDFA
La siguiente tabla enumera las diferencias entre DFA y NDFA.
| DFA | NDFA |
|---|---|
| La transición de un estado es a un único estado siguiente en particular para cada símbolo de entrada. Por eso se llama determinista . | La transición de un estado puede ser a varios estados siguientes para cada símbolo de entrada. Por eso se le llama no determinista . |
| Las transiciones de cadenas vacías no se ven en DFA. | NDFA permite transiciones de cadenas vacías. |
| El retroceso está permitido en DFA | En NDFA, el retroceso no siempre es posible. |
| Requiere más espacio. | Requiere menos espacio. |
| Una cadena es aceptada por un DFA, si pasa a un estado final. | Una cadena es aceptada por un NDFA, si al menos una de todas las posibles transiciones termina en un estado final. |
Aceptadores, clasificadores y transductores
Aceptador (reconocedor)
Un autómata que calcula una función booleana se llama acceptor. Todos los estados de un aceptor son aceptar o rechazar las entradas que se le dan.
Clasificador
UN classifier tiene más de dos estados finales y da una única salida cuando termina.
Transductor
Un autómata que produce salidas basadas en la entrada actual y / o el estado anterior se llama transducer. Los transductores pueden ser de dos tipos:
Mealy Machine - La salida depende tanto del estado actual como de la entrada actual.
Moore Machine - La salida depende solo del estado actual.
Aceptabilidad por DFA y NDFA
Una cadena es aceptada por un DFA / NDFA si el DFA / NDFA que comienza en el estado inicial termina en un estado de aceptación (cualquiera de los estados finales) después de leer la cadena por completo.
Una cadena S es aceptada por un DFA / NDFA (Q, ∑, δ, q 0 , F), si
δ*(q0, S) ∈ F
El idioma L aceptado por DFA / NDFA es
{S | S ∈ ∑* and δ*(q0, S) ∈ F}
Una cadena S ′ no es aceptada por un DFA / NDFA (Q, ∑, δ, q 0 , F), iff
δ*(q0, S′) ∉ F
El idioma L ′ no aceptado por DFA / NDFA (Complemento del idioma aceptado L) es
{S | S ∈ ∑* and δ*(q0, S) ∉ F}
Example
Consideremos el DFA que se muestra en la Figura 1.3. Del DFA, se pueden derivar las cadenas aceptables.

Cadenas aceptadas por el DFA anterior: {0, 00, 11, 010, 101, ...........}
Cadenas no aceptadas por el DFA anterior: {1, 011, 111, ........}
Planteamiento del problema
Dejar X = (Qx, ∑, δx, q0, Fx)Ser un NDFA que acepte el lenguaje L (X). Tenemos que diseñar un DFA equivalenteY = (Qy, ∑, δy, q0, Fy) tal que L(Y) = L(X). El siguiente procedimiento convierte el NDFA en su DFA equivalente:
Algoritmo
Input - Un NDFA
Output - Un DFA equivalente
Step 1 - Crear tabla de estado a partir del NDFA dado.
Step 2 - Cree una tabla de estado en blanco bajo posibles alfabetos de entrada para el DFA equivalente.
Step 3 - Marque el estado de inicio del DFA con q0 (Igual que el NDFA).
Step 4- Descubra la combinación de estados {Q 0 , Q 1 , ..., Q n } para cada posible alfabeto de entrada.
Step 5 - Cada vez que generamos un nuevo estado DFA bajo las columnas del alfabeto de entrada, tenemos que aplicar el paso 4 nuevamente; de lo contrario, vaya al paso 6.
Step 6 - Los estados que contienen cualquiera de los estados finales del NDFA son los estados finales del DFA equivalente.
Ejemplo
Consideremos el NDFA que se muestra en la figura siguiente.

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| un | {a B C D e} | {Delaware} |
| segundo | {C} | {mi} |
| C | ∅ | {segundo} |
| re | {mi} | ∅ |
| mi | ∅ | ∅ |
Usando el algoritmo anterior, encontramos su DFA equivalente. La tabla de estado del DFA se muestra a continuación.
| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| [un] | [a B C D e] | [Delaware] |
| [a B C D e] | [a B C D e] | [b, d, e] |
| [Delaware] | [mi] | ∅ |
| [b, d, e] | [c, e] | [mi] |
| [mi] | ∅ | ∅ |
| [c, e] | ∅ | [segundo] |
| [segundo] | [C] | [mi] |
| [C] | ∅ | [segundo] |
El diagrama de estado del DFA es el siguiente:

Minimización de DFA mediante el teorema de Myhill-Nerode
Algoritmo
Input - DFA
Output - DFA minimizado
Step 1- Dibuje una tabla para todos los pares de estados (Q i , Q j ) no necesariamente conectados directamente [Todos están sin marcar inicialmente]
Step 2- Considere cada par de estados (Q i , Q j ) en el DFA donde Q i ∈ F y Q j ∉ F o viceversa y márquelos. [Aquí F es el conjunto de estados finales]
Step 3 - Repita este paso hasta que no podamos marcar más estados -
Si hay un par sin marcar (Q i , Q j ), márquelo si el par {δ (Q i , A), δ (Q i , A)} está marcado para algún alfabeto de entrada.
Step 4- Combinar todos los pares sin marcar (Q i , Q j ) y convertirlos en un solo estado en el DFA reducido.
Ejemplo
Usemos el algoritmo 2 para minimizar el DFA que se muestra a continuación.

Step 1 - Dibujamos una tabla para todos los pares de estados.
| un | segundo | C | re | mi | F | |
| un | ||||||
| segundo | ||||||
| C | ||||||
| re | ||||||
| mi | ||||||
| F |
Step 2 - Marcamos los pares de estados.
| un | segundo | C | re | mi | F | |
| un | ||||||
| segundo | ||||||
| C | ✔ | ✔ | ||||
| re | ✔ | ✔ | ||||
| mi | ✔ | ✔ | ||||
| F | ✔ | ✔ | ✔ |
Step 3- Intentaremos marcar los pares de estados, con una marca de verificación de color verde, de forma transitiva. Si ingresamos 1 para indicar 'a' y 'f', irá al estado 'c' y 'f' respectivamente. (c, f) ya está marcado, por lo tanto marcaremos el par (a, f). Ahora, ingresamos 1 para indicar 'b' y 'f'; irá al estado 'd' y 'f' respectivamente. (d, f) ya está marcado, por lo que marcaremos el par (b, f).
| un | segundo | C | re | mi | F | |
| un | ||||||
| segundo | ||||||
| C | ✔ | ✔ | ||||
| re | ✔ | ✔ | ||||
| mi | ✔ | ✔ | ||||
| F | ✔ | ✔ | ✔ | ✔ | ✔ |
Después del paso 3, tenemos combinaciones de estados {a, b} {c, d} {c, e} {d, e} que no están marcadas.
Podemos recombinar {c, d} {c, e} {d, e} en {c, d, e}
Por lo tanto, obtuvimos dos estados combinados como: {a, b} y {c, d, e}
Por lo tanto, el DFA minimizado final contendrá tres estados {f}, {a, b} y {c, d, e}
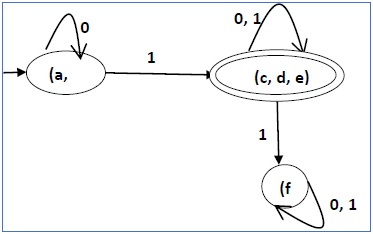
Minimización de DFA mediante el teorema de equivalencia
Si X e Y son dos estados en un DFA, podemos combinar estos dos estados en {X, Y} si no son distinguibles. Se pueden distinguir dos estados, si hay al menos una cadena S, de modo que uno de δ (X, S) y δ (Y, S) acepta y otro no acepta. Por lo tanto, un DFA es mínimo si y solo si todos los estados son distinguibles.
Algoritmo 3
Step 1 - Todos los estados Q están divididos en dos particiones - final states y non-final states y se denotan por P0. Todos los estados de una partición son 0º equivalentes. Tomar un contadork e inicializarlo con 0.
Step 2- Incrementar k en 1. Para cada partición en P k , divida los estados en P k en dos particiones si son k-distinguibles. Dos estados dentro de esta partición X e Y son k-distinguibles si hay una entradaS tal que δ(X, S) y δ(Y, S) son (k-1) -distinguible.
Step 3- Si P k ≠ P k-1 , repita el paso 2; de lo contrario, vaya al paso 4.
Step 4- Combinar k- ésimo conjuntos equivalentes y convertirlos en los nuevos estados del DFA reducido.
Ejemplo
Consideremos el siguiente DFA:

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| un | segundo | C |
| segundo | un | re |
| C | mi | F |
| re | mi | F |
| mi | mi | F |
| F | F | F |
Apliquemos el algoritmo anterior al DFA anterior:
- P 0 = {(c, d, e), (a, b, f)}
- P 1 = {(c, d, e), (a, b), (f)}
- P 2 = {(c, d, e), (a, b), (f)}
Por tanto, P 1 = P 2 .
Hay tres estados en el DFA reducido. El DFA reducido es el siguiente:
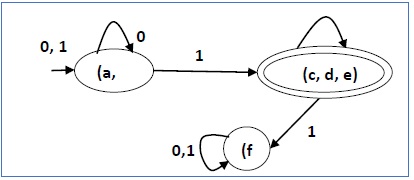
| Q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| (a, b) | (a, b) | (c, d, e) |
| (c, d, e) | (c, d, e) | (F) |
| (F) | (F) | (F) |
Los autómatas finitos pueden tener salidas correspondientes a cada transición. Hay dos tipos de máquinas de estados finitos que generan resultados:
- Máquina harinosa
- Máquina de moore
Máquina harinosa
Una Mealy Machine es un FSM cuya salida depende tanto del estado actual como de la entrada actual.
Puede ser descrito por una tupla 6 (Q, ∑, O, δ, X, q 0 ) donde -
Q es un conjunto finito de estados.
∑ es un conjunto finito de símbolos llamado alfabeto de entrada.
O es un conjunto finito de símbolos llamado alfabeto de salida.
δ es la función de transición de entrada donde δ: Q × ∑ → Q
X es la función de transición de salida donde X: Q × ∑ → O
q0es el estado inicial desde donde se procesa cualquier entrada (q 0 ∈ Q).
La tabla de estado de una máquina de harina se muestra a continuación:
| Estado actual | Siguiente estado | |||
|---|---|---|---|---|
| entrada = 0 | entrada = 1 | |||
| Estado | Salida | Estado | Salida | |
| → un | segundo | x 1 | C | x 1 |
| segundo | segundo | x 2 | re | x 3 |
| C | re | x 3 | C | x 1 |
| re | re | x 3 | re | x 2 |
El diagrama de estado de la Mealy Machine anterior es:

Máquina de Moore
La máquina de Moore es una FSM cuyas salidas dependen únicamente del estado actual.
Una máquina de Moore se puede describir mediante una tupla de 6 (Q, ∑, O, δ, X, q 0 ) donde -
Q es un conjunto finito de estados.
∑ es un conjunto finito de símbolos llamado alfabeto de entrada.
O es un conjunto finito de símbolos llamado alfabeto de salida.
δ es la función de transición de entrada donde δ: Q × ∑ → Q
X es la función de transición de salida donde X: Q → O
q0es el estado inicial desde donde se procesa cualquier entrada (q 0 ∈ Q).
La tabla de estado de una máquina Moore se muestra a continuación:
| Estado actual | Estado siguiente | Salida | |
|---|---|---|---|
| Entrada = 0 | Entrada = 1 | ||
| → un | segundo | C | x 2 |
| segundo | segundo | re | x 1 |
| C | C | re | x 2 |
| re | re | re | x 3 |
El diagrama de estado de la máquina de Moore anterior es:

Mealy Machine vs.Moore Machine
La siguiente tabla destaca los puntos que diferencian una máquina harinosa de una máquina Moore.
| Máquina harinosa | Máquina de Moore |
|---|---|
| La salida depende tanto del estado actual como de la entrada actual | La salida depende solo del estado actual. |
| Generalmente, tiene menos estados que Moore Machine. | Generalmente, tiene más estados que Mealy Machine. |
| El valor de la función de salida es una función de las transiciones y los cambios, cuando se realiza la lógica de entrada en el estado actual. | El valor de la función de salida es una función del estado actual y los cambios en los bordes del reloj, siempre que ocurren cambios de estado. |
| Las máquinas harinosas reaccionan más rápido a las entradas. Generalmente reaccionan en el mismo ciclo de reloj. | En las máquinas Moore, se requiere más lógica para decodificar las salidas, lo que genera más retrasos en el circuito. Generalmente reaccionan un ciclo de reloj más tarde. |
Máquina Moore a Máquina harinosa
Algoritmo 4
Input - Máquina de Moore
Output - Máquina harinosa
Step 1 - Tome un formato de tabla de transición de Mealy Machine en blanco.
Step 2 - Copie todos los estados de transición de Moore Machine en este formato de tabla.
Step 3- Verificar los estados actuales y sus correspondientes salidas en la tabla de estados de Moore Machine; si para un estado Q i la salida es m, cópiela en las columnas de salida de la tabla de estado de Mealy Machine dondequiera que Q i aparezca en el siguiente estado.
Ejemplo
Consideremos la siguiente máquina de Moore:
| Estado actual | Estado siguiente | Salida | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → un | re | segundo | 1 |
| segundo | un | re | 0 |
| C | C | C | 0 |
| re | segundo | un | 1 |
Ahora aplicamos el algoritmo 4 para convertirlo en Mealy Machine.
Step 1 & 2 -
| Estado actual | Estado siguiente | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Estado | Salida | Estado | Salida | |
| → un | re | segundo | ||
| segundo | un | re | ||
| C | C | C | ||
| re | segundo | un | ||
Step 3 -
| Estado actual | Estado siguiente | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Estado | Salida | Estado | Salida | |
| => a | re | 1 | segundo | 0 |
| segundo | un | 1 | re | 1 |
| C | C | 0 | C | 0 |
| re | segundo | 0 | un | 1 |
Mealy Machine a Moore Machine
Algoritmo 5
Input - Máquina harinosa
Output - Máquina de Moore
Step 1- Calcule el número de salidas diferentes para cada estado (Q i ) que están disponibles en la tabla de estados de la máquina Mealy.
Step 2- Si todas las salidas de Qi son iguales, copie el estado Q i . Si tiene n salidas distintas, divida Q i en n estados como Q en donden = 0, 1, 2 .......
Step 3 - Si la salida del estado inicial es 1, inserte un nuevo estado inicial al principio que da una salida 0.
Ejemplo
Consideremos la siguiente máquina harinosa:
| Estado actual | Estado siguiente | |||
|---|---|---|---|---|
| a = 0 | a = 1 | |||
| Estado siguiente | Salida | Estado siguiente | Salida | |
| → un | re | 0 | segundo | 1 |
| segundo | un | 1 | re | 0 |
| C | C | 1 | C | 0 |
| re | segundo | 0 | un | 1 |
Aquí, los estados 'a' y 'd' dan solo salidas 1 y 0 respectivamente, por lo que retenemos los estados 'a' y 'd'. Pero los estados 'b' y 'c' producen salidas diferentes (1 y 0). Entonces, dividimosb dentro b0, b1 y c dentro c0, c1.
| Estado actual | Estado siguiente | Salida | |
|---|---|---|---|
| a = 0 | a = 1 | ||
| → un | re | b 1 | 1 |
| b 0 | un | re | 0 |
| b 1 | un | re | 1 |
| c 0 | c 1 | C 0 | 0 |
| c 1 | c 1 | C 0 | 1 |
| re | b 0 | un | 0 |
En el sentido literario del término, las gramáticas denotan reglas sintácticas para la conversación en lenguajes naturales. La lingüística ha intentado definir las gramáticas desde el inicio de los lenguajes naturales como el inglés, el sánscrito, el mandarín, etc.
La teoría de los lenguajes formales encuentra su aplicabilidad ampliamente en los campos de la informática. Noam Chomsky dio un modelo matemático de gramática en 1956 que es eficaz para escribir lenguajes informáticos.
Gramática
Una gramática G se puede escribir formalmente como una tupla de 4 (N, T, S, P) donde -
N o VN es un conjunto de variables o símbolos no terminales.
T o ∑ es un conjunto de símbolos de Terminal.
S es una variable especial llamada símbolo de inicio, S ∈ N
Pes reglas de producción para terminales y no terminales. Una regla de producción tiene la forma α → β, donde α y β son cuerdas en V N ∪ Σ y menos un símbolo de α pertenece a V N .
Ejemplo
Gramática G1 -
({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})
Aquí,
S, A, y B son símbolos no terminales;
a y b son símbolos de terminal
S es el símbolo de Inicio, S ∈ N
Producciones, P : S → AB, A → a, B → b
Ejemplo
Gramática G2 -
(({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Aquí,
S y A son símbolos no terminales.
a y b son símbolos terminales.
ε es una cadena vacía.
S es el símbolo de Inicio, S ∈ N
Producción P : S → aAb, aA → aaAb, A → ε
Derivaciones de una gramática
Las cadenas pueden derivarse de otras cadenas utilizando las producciones en una gramática. Si una gramáticaG tiene una produccion α → β, podemos decir eso x α y deriva x β y en G. Esta derivación se escribe como:
x α y ⇒G x β y
Ejemplo
Consideremos la gramática:
G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})
Algunas de las cadenas que se pueden derivar son:
S ⇒ aA b usando producción S → aAb
⇒ a aA bb usando producción aA → aAb
⇒ aaa A bbb usando producción aA → aAb
⇒ aaabbb usando producción A → ε
Se dice que el conjunto de todas las cadenas que se pueden derivar de una gramática es el lenguaje generado a partir de esa gramática. Un lenguaje generado por una gramáticaG es un subconjunto definido formalmente por
L (G) = {W | W ∈ ∑ *, S ⇒ G W }
Si L(G1) = L(G2), la gramática G1 es equivalente a la gramática G2.
Ejemplo
Si hay una gramática
G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}
aquí S produce ABy podemos reemplazar A por ay B por b. Aquí, la única cadena aceptada esab, es decir,
L (G) = {ab}
Ejemplo
Supongamos que tenemos la siguiente gramática:
G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA | a, B → bB | b}
El lenguaje generado por esta gramática -
L (G) = {ab, a 2 b, ab 2 , a 2 b 2 , ………}
= {a m b n | m ≥ 1 yn ≥ 1}
Construcción de una gramática que genera un lenguaje
Consideraremos algunos idiomas y los convertiremos en una gramática G que produce esos idiomas.
Ejemplo
Problem- Suponga, L (G) = {a m b n | m ≥ 0 yn> 0}. Tenemos que averiguar la gramáticaG que produce L(G).
Solution
Dado que L (G) = {a m b n | m ≥ 0 y n> 0}
el conjunto de cadenas aceptadas se puede reescribir como -
L (G) = {b, ab, bb, aab, abb, …….}
Aquí, el símbolo de inicio debe tener al menos una 'b' precedida de cualquier número de 'a', incluido el nulo.
Para aceptar el conjunto de cadenas {b, ab, bb, aab, abb, …….}, Hemos tomado las producciones -
S → aS, S → B, B → by B → bB
S → B → b (aceptado)
S → B → bB → bb (aceptado)
S → aS → aB → ab (Aceptado)
S → aS → aaS → aaB → aab (Aceptado)
S → aS → aB → abB → abb (Aceptado)
Por lo tanto, podemos probar que cada cadena en L (G) es aceptada por el lenguaje generado por el conjunto de producción.
De ahí la gramática:
G: ({S, A, B}, {a, b}, S, {S → aS | B, B → b | bB})
Ejemplo
Problem- Suponga, L (G) = {a m b n | m> 0 y n ≥ 0}. Tenemos que averiguar la gramática G que produce L (G).
Solution -
Dado que L (G) = {a m b n | m> 0 y n ≥ 0}, el conjunto de cadenas aceptadas se puede reescribir como -
L (G) = {a, aa, ab, aaa, aab, abb, …….}
Aquí, el símbolo de inicio tiene que tomar al menos una 'a' seguida de cualquier número de 'b', incluido el nulo.
Para aceptar el conjunto de cadenas {a, aa, ab, aaa, aab, abb, …….}, Hemos tomado las producciones -
S → aA, A → aA, A → B, B → bB, B → λ
S → aA → aB → aλ → a (Aceptado)
S → aA → aaA → aaB → aaλ → aa (Aceptado)
S → aA → aB → abB → abλ → ab (Aceptado)
S → aA → aaA → aaaA → aaaB → aaaλ → aaa (Aceptado)
S → aA → aaA → aaB → aabB → aabλ → aab (Aceptado)
S → aA → aB → abB → abbB → abbλ → abb (Aceptado)
Por lo tanto, podemos probar que cada cadena en L (G) es aceptada por el lenguaje generado por el conjunto de producción.
De ahí la gramática:
G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB})
Según Noam Chomosky, hay cuatro tipos de gramáticas: tipo 0, tipo 1, tipo 2 y tipo 3. La siguiente tabla muestra cómo se diferencian entre sí:
| Tipo de gramática | Gramática aceptada | Idioma aceptado | Autómata |
|---|---|---|---|
| Tipo 0 | Gramática sin restricciones | Lenguaje recursivamente enumerable | Máquina de Turing |
| Tipo 1 | Gramática sensible al contexto | Lenguaje sensible al contexto | Autómata delimitado lineal |
| Tipo 2 | Gramática libre de contexto | Lenguaje libre de contexto | Autómata de empuje |
| Tipo 3 | Gramática regular | Lengua regular | Autómata de estado finito |
Observe la siguiente ilustración. Muestra el alcance de cada tipo de gramática:

Tipo - 3 gramática
Type-3 grammarsgenerar lenguajes regulares. Las gramáticas de tipo 3 deben tener un solo no terminal en el lado izquierdo y un lado derecho que consta de un solo terminal o un solo terminal seguido de un solo no terminal.
Las producciones deben estar en la forma X → a or X → aY
dónde X, Y ∈ N (No terminal)
y a ∈ T (Terminal)
La regla S → ε está permitido si S no aparece en el lado derecho de ninguna regla.
Ejemplo
X → ε
X → a | aY
Y → bTipo - 2 gramática
Type-2 grammars generar lenguajes libres de contexto.
The productions must be in the form A → γ
where A ∈ N (Non terminal)
and γ ∈ (T ∪ N)* (String of terminals and non-terminals).
These languages generated by these grammars are be recognized by a non-deterministic pushdown automaton.
Example
S → X a
X → a
X → aX
X → abc
X → εType - 1 Grammar
Type-1 grammars generate context-sensitive languages. The productions must be in the form
α A β → α γ β
where A ∈ N (Non-terminal)
and α, β, γ ∈ (T ∪ N)* (Strings of terminals and non-terminals)
The strings α and β may be empty, but γ must be non-empty.
The rule S → ε is allowed if S does not appear on the right side of any rule. The languages generated by these grammars are recognized by a linear bounded automaton.
Example
AB → AbBc
A → bcA
B → bType - 0 Grammar
Type-0 grammars generate recursively enumerable languages. The productions have no restrictions. They are any phase structure grammar including all formal grammars.
They generate the languages that are recognized by a Turing machine.
The productions can be in the form of α → β where α is a string of terminals and nonterminals with at least one non-terminal and α cannot be null. β is a string of terminals and non-terminals.
Example
S → ACaB
Bc → acB
CB → DB
aD → DbA Regular Expression can be recursively defined as follows −
ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
φ is a Regular Expression denoting an empty language. (L (φ) = { })
x is a Regular Expression where L = {x}
If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then
X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).
X . Y is a Regular Expression corresponding to the language L(X) . L(Y) where L(X.Y) = L(X) . L(Y)
R* is a Regular Expression corresponding to the language L(R*)where L(R*) = (L(R))*
If we apply any of the rules several times from 1 to 5, they are Regular Expressions.
Some RE Examples
| Regular Expressions | Regular Set |
|---|---|
| (0 + 10*) | L = { 0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | L = {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | L = {ε, 0, 1, 01} |
| (a+b)* | Set of strings of a’s and b’s of any length including the null string. So L = { ε, a, b, aa , ab , bb , ba, aaa…….} |
| (a+b)*abb | Set of strings of a’s and b’s ending with the string abb. So L = {abb, aabb, babb, aaabb, ababb, …………..} |
| (11)* | Set consisting of even number of 1’s including empty string, So L= {ε, 11, 1111, 111111, ……….} |
| (aa)*(bb)*b | Set of strings consisting of even number of a’s followed by odd number of b’s , so L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..} |
| (aa + ab + ba + bb)* | String of a’s and b’s of even length can be obtained by concatenating any combination of the strings aa, ab, ba and bb including null, so L = {aa, ab, ba, bb, aaab, aaba, …………..} |
Any set that represents the value of the Regular Expression is called a Regular Set.
Properties of Regular Sets
Property 1. The union of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(aa)* and RE2 = (aa)*
So, L1 = {a, aaa, aaaaa,.....} (Strings of odd length excluding Null)
and L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}
(Strings of all possible lengths including Null)
RE (L1 ∪ L2) = a* (which is a regular expression itself)
Hence, proved.
Property 2. The intersection of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(a*) and RE2 = (aa)*
So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)
RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.
Hence, proved.
Property 3. The complement of a regular set is regular.
Proof −
Let us take a regular expression −
RE = (aa)*
So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)
Complement of L is all the strings that is not in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
RE (L’) = a(aa)* which is a regular expression itself.
Hence, proved.
Property 4. The difference of two regular set is regular.
Proof −
Let us take two regular expressions −
RE1 = a (a*) and RE2 = (aa)*
So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(Strings of all odd lengths excluding Null)
RE (L1 – L2) = a (aa)* which is a regular expression.
Hence, proved.
Property 5. The reversal of a regular set is regular.
Proof −
We have to prove LR is also regular if L is a regular set.
Let, L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10 which is regular
Hence, proved.
Property 6. The closure of a regular set is regular.
Proof −
If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)
i.e., RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)
RE (L*) = a (a)*
Hence, proved.
Property 7. The concatenation of two regular sets is regular.
Proof −
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
and L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
Identities Related to Regular Expressions
Given R, P, L, Q as regular expressions, the following identities hold −
- ∅* = ε
- ε* = ε
- RR* = R*R
- R*R* = R*
- (R*)* = R*
- RR* = R*R
- (PQ)*P =P(QP)*
- (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
- R + ∅ = ∅ + R = R (The identity for union)
- R ε = ε R = R (The identity for concatenation)
- ∅ L = L ∅ = ∅ (The annihilator for concatenation)
- R + R = R (Idempotent law)
- L (M + N) = LM + LN (Left distributive law)
- (M + N) L = ML + NL (Right distributive law)
- ε + RR* = ε + R*R = R*
In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.
Statement −
Let P and Q be two regular expressions.
If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*
Proof −
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the following equation −
R = Q + QP + QP2 + QP3…..
R = Q (ε + P + P2 + P3 + …. )
R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]
Hence, proved.
Assumptions for Applying Arden’s Theorem
- The transition diagram must not have NULL transitions
- It must have only one initial state
Method
Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q1.
q1 = q1R11 + q2R21 + … + qnRn1 + ε
q2 = q1R12 + q2R22 + … + qnRn2
…………………………
…………………………
…………………………
…………………………
qn = q1R1n + q2R2n + … + qnRnn
Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅
Step 2 − Solve these equations to get the equation for the final state in terms of Rij
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state and final state is q1.
The equations for the three states q1, q2, and q3 are as follows −
q1 = q1a + q3a + ε (ε move is because q1 is the initial state0
q2 = q1b + q2b + q3b
q3 = q2a
Now, we will solve these three equations −
q2 = q1b + q2b + q3b
= q1b + q2b + (q2a)b (Substituting value of q3)
= q1b + q2(b + ab)
= q1b (b + ab)* (Applying Arden’s Theorem)
q1 = q1a + q3a + ε
= q1a + q2aa + ε (Substituting value of q3)
= q1a + q1b(b + ab*)aa + ε (Substituting value of q2)
= q1(a + b(b + ab)*aa) + ε
= ε (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*.
Problem
Construct a regular expression corresponding to the automata given below −

Solution −
Here the initial state is q1 and the final state is q2
Now we write down the equations −
q1 = q10 + ε
q2 = q11 + q20
q3 = q21 + q30 + q31
Now, we will solve these three equations −
q1 = ε0* [As, εR = R]
So, q1 = 0*
q2 = 0*1 + q20
So, q2 = 0*1(0)* [By Arden’s theorem]
Hence, the regular expression is 0*10*.
We can use Thompson's Construction to find out a Finite Automaton from a Regular Expression. We will reduce the regular expression into smallest regular expressions and converting these to NFA and finally to DFA.
Some basic RA expressions are the following −
Case 1 − For a regular expression ‘a’, we can construct the following FA −

Case 2 − For a regular expression ‘ab’, we can construct the following FA −

Case 3 − For a regular expression (a+b), we can construct the following FA −

Case 4 − For a regular expression (a+b)*, we can construct the following FA −

Method
Step 1 Construct an NFA with Null moves from the given regular expression.
Step 2 Remove Null transition from the NFA and convert it into its equivalent DFA.
Problem
Convert the following RA into its equivalent DFA − 1 (0 + 1)* 0
Solution
We will concatenate three expressions "1", "(0 + 1)*" and "0"

Now we will remove the ε transitions. After we remove the ε transitions from the NDFA, we get the following −

It is an NDFA corresponding to the RE − 1 (0 + 1)* 0. If you want to convert it into a DFA, simply apply the method of converting NDFA to DFA discussed in Chapter 1.
Finite Automata with Null Moves (NFA-ε)
A Finite Automaton with null moves (FA-ε) does transit not only after giving input from the alphabet set but also without any input symbol. This transition without input is called a null move.
An NFA-ε is represented formally by a 5-tuple (Q, ∑, δ, q0, F), consisting of
Q − a finite set of states
∑ − a finite set of input symbols
δ − a transition function δ : Q × (∑ ∪ {ε}) → 2Q
q0 − an initial state q0 ∈ Q
F − a set of final state/states of Q (F⊆Q).

The above (FA-ε) accepts a string set − {0, 1, 01}
Removal of Null Moves from Finite Automata
If in an NDFA, there is ϵ-move between vertex X to vertex Y, we can remove it using the following steps −
- Find all the outgoing edges from Y.
- Copy all these edges starting from X without changing the edge labels.
- If X is an initial state, make Y also an initial state.
- If Y is a final state, make X also a final state.
Problem
Convert the following NFA-ε to NFA without Null move.

Solution
Step 1 −
Here the ε transition is between q1 and q2, so let q1 is X and qf is Y.
Here the outgoing edges from qf is to qf for inputs 0 and 1.
Step 2 −
Now we will Copy all these edges from q1 without changing the edges from qf and get the following FA −

Step 3 −
Here q1 is an initial state, so we make qf also an initial state.
So the FA becomes −

Step 4 −
Here qf is a final state, so we make q1 also a final state.
So the FA becomes −

Theorem
Let L be a regular language. Then there exists a constant ‘c’ such that for every string w in L −
|w| ≥ c
We can break w into three strings, w = xyz, such that −
- |y| > 0
- |xy| ≤ c
- For all k ≥ 0, the string xykz is also in L.
Applications of Pumping Lemma
Pumping Lemma is to be applied to show that certain languages are not regular. It should never be used to show a language is regular.
If L is regular, it satisfies Pumping Lemma.
If L does not satisfy Pumping Lemma, it is non-regular.
Method to prove that a language L is not regular
At first, we have to assume that L is regular.
So, the pumping lemma should hold for L.
Use the pumping lemma to obtain a contradiction −
Select w such that |w| ≥ c
Select y such that |y| ≥ 1
Select x such that |xy| ≤ c
Assign the remaining string to z.
Select k such that the resulting string is not in L.
Hence L is not regular.
Problem
Prove that L = {aibi | i ≥ 0} is not regular.
Solution −
At first, we assume that L is regular and n is the number of states.
Let w = anbn. Thus |w| = 2n ≥ n.
By pumping lemma, let w = xyz, where |xy| ≤ n.
Let x = ap, y = aq, and z = arbn, where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
Let k = 2. Then xy2z = apa2qarbn.
Number of as = (p + 2q + r) = (p + q + r) + q = n + q
Hence, xy2z = an+q bn. Since q ≠ 0, xy2z is not of the form anbn.
Thus, xy2z is not in L. Hence L is not regular.
If (Q, ∑, δ, q0, F) be a DFA that accepts a language L, then the complement of the DFA can be obtained by swapping its accepting states with its non-accepting states and vice versa.
We will take an example and elaborate this below −

This DFA accepts the language
L = {a, aa, aaa , ............. }
over the alphabet
∑ = {a, b}
So, RE = a+.
Now we will swap its accepting states with its non-accepting states and vice versa and will get the following −

This DFA accepts the language
Ľ = {ε, b, ab ,bb,ba, ............... }
over the alphabet
∑ = {a, b}
Note − If we want to complement an NFA, we have to first convert it to DFA and then have to swap states as in the previous method.
Definition − A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where
N is a set of non-terminal symbols.
T is a set of terminals where N ∩ T = NULL.
P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.
S is the start symbol.
Example
- The grammar ({A}, {a, b, c}, P, A), P : A → aA, A → abc.
- The grammar ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- The grammar ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Generation of Derivation Tree
A derivation tree or parse tree is an ordered rooted tree that graphically represents the semantic information a string derived from a context-free grammar.
Representation Technique
Root vertex − Must be labeled by the start symbol.
Vertex − Labeled by a non-terminal symbol.
Leaves − Labeled by a terminal symbol or ε.
If S → x1x2 …… xn is a production rule in a CFG, then the parse tree / derivation tree will be as follows −

There are two different approaches to draw a derivation tree −
Top-down Approach −
Starts with the starting symbol S
Goes down to tree leaves using productions
Bottom-up Approach −
Starts from tree leaves
Proceeds upward to the root which is the starting symbol S
Derivation or Yield of a Tree
The derivation or the yield of a parse tree is the final string obtained by concatenating the labels of the leaves of the tree from left to right, ignoring the Nulls. However, if all the leaves are Null, derivation is Null.
Example
Let a CFG {N,T,P,S} be
N = {S}, T = {a, b}, Starting symbol = S, P = S → SS | aSb | ε
One derivation from the above CFG is “abaabb”
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Sentential Form and Partial Derivation Tree
A partial derivation tree is a sub-tree of a derivation tree/parse tree such that either all of its children are in the sub-tree or none of them are in the sub-tree.
Example
If in any CFG the productions are −
S → AB, A → aaA | ε, B → Bb| ε
the partial derivation tree can be the following −
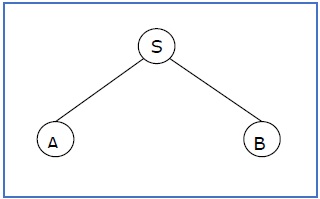
If a partial derivation tree contains the root S, it is called a sentential form. The above sub-tree is also in sentential form.
Leftmost and Rightmost Derivation of a String
Leftmost derivation − A leftmost derivation is obtained by applying production to the leftmost variable in each step.
Rightmost derivation − A rightmost derivation is obtained by applying production to the rightmost variable in each step.
Example
Let any set of production rules in a CFG be
X → X+X | X*X |X| a
over an alphabet {a}.
The leftmost derivation for the string "a+a*a" may be −
X → X+X → a+X → a + X*X → a+a*X → a+a*a
La derivación paso a paso de la cadena anterior se muestra a continuación:

La derivación más a la derecha de la cadena anterior "a+a*a" puede ser -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
La derivación paso a paso de la cadena anterior se muestra a continuación:

Gramáticas recursivas izquierda y derecha
En una gramática libre de contexto G, si hay una producción en forma X → Xa dónde X es un no terminal y ‘a’ es una cadena de terminales, se llama left recursive production. La gramática que tiene una producción recursiva a la izquierda se llamaleft recursive grammar.
Y si en una gramática libre de contexto G, si hay una producción está en la forma X → aX dónde X es un no terminal y ‘a’ es una cadena de terminales, se llama right recursive production. La gramática que tiene una producción recursiva correcta se llamaright recursive grammar.
Si una gramática libre de contexto G tiene más de un árbol de derivación para alguna cadena w ∈ L(G), se llama ambiguous grammar. Existen múltiples derivaciones hacia la derecha o hacia la izquierda para alguna cadena generada a partir de esa gramática.
Problema
Compruebe si la gramática G con reglas de producción -
X → X + X | X * X | X | un
es ambiguo o no.
Solución
Averigüemos el árbol de derivación de la cadena "a + a * a". Tiene dos derivaciones más a la izquierda.
Derivation 1- X → X + X → a + X → a + X * X → a + a * X → a + a * a
Parse tree 1 -

Derivation 2- X → X * X → X + X * X → a + X * X → a + a * X → a + a * a
Parse tree 2 -

Como hay dos árboles de análisis para una sola cadena "a + a * a", la gramática G es ambiguo.
Los lenguajes libres de contexto son closed bajo -
- Union
- Concatenation
- Operación Kleene Star
Unión
Sean L 1 y L 2 dos lenguajes libres de contexto. Entonces L 1 ∪ L 2 también está libre de contexto.
Ejemplo
Sea L 1 = {a n b n , n> 0}. La gramática correspondiente G 1 tendrá P: S1 → aAb | ab
Sea L 2 = {c m d m , m ≥ 0}. La gramática correspondiente G 2 tendrá P: S2 → cBb | ε
Unión de L 1 y L 2 , L = L 1 ∪ L 2 = {a n b n } ∪ {c m d m }
La gramática correspondiente G tendrá la producción adicional S → S1 | S2
Concatenación
Si L 1 y L 2 son lenguajes libres de contexto, entonces L 1 L 2 también lo está.
Ejemplo
Unión de las lenguas L 1 y L 2 , L = L 1 L 2 = {a n b n c m d m }
La gramática correspondiente G tendrá la producción adicional S → S1 S2
Estrella de Kleene
Si L es un lenguaje sin contexto, entonces L * también lo está.
Ejemplo
Sea L = {a n b n , n ≥ 0}. La gramática correspondiente G tendrá P: S → aAb | ε
Estrella de Kleene L 1 = {a n b n } *
La gramática correspondiente G 1 tendrá producciones adicionales S1 → SS 1 | ε
Los lenguajes libres de contexto son not closed bajo -
Intersection - Si L1 y L2 son lenguajes libres de contexto, entonces L1 ∩ L2 no es necesariamente libre de contexto.
Intersection with Regular Language - Si L1 es un idioma regular y L2 es un idioma sin contexto, entonces L1 ∩ L2 es un idioma sin contexto.
Complement - Si L1 es un lenguaje sin contexto, entonces L1 'puede no estar libre de contexto.
En un CFG, puede suceder que no se necesiten todas las reglas y símbolos de producción para la derivación de cadenas. Además, puede haber algunas producciones nulas y producciones unitarias. La eliminación de estas producciones y símbolos se llamasimplification of CFGs. La simplificación se compone esencialmente de los siguientes pasos:
- Reducción de CFG
- Eliminación de unidades de producción
- Eliminación de producciones nulas
Reducción de CFG
Los CFG se reducen en dos fases:
Phase 1 - Derivación de una gramática equivalente, G’, del CFG, G, de modo que cada variable derive alguna cadena terminal.
Derivation Procedure -
Paso 1: incluya todos los símbolos, W1, que derivan algún terminal e inicializan i=1.
Paso 2: incluye todos los símbolos, Wi+1, que derivan Wi.
Paso 3 - Incremento i y repita el Paso 2, hasta Wi+1 = Wi.
Paso 4: incluya todas las reglas de producción que Wi en eso.
Phase 2 - Derivación de una gramática equivalente, G”, del CFG, G’, de modo que cada símbolo aparece en forma de oración.
Derivation Procedure -
Paso 1: incluya el símbolo de inicio en Y1 e inicializar i = 1.
Paso 2: incluye todos los símbolos, Yi+1, que puede derivarse de Yi e incluir todas las reglas de producción que se hayan aplicado.
Paso 3 - Incremento i y repita el Paso 2, hasta Yi+1 = Yi.
Problema
Encuentre una gramática reducida equivalente a la gramática G, que tenga reglas de producción, P: S → AC | B, A → a, C → c | BC, E → aA | mi
Solución
Phase 1 -
T = {a, c, e}
W 1 = {A, C, E} de las reglas A → a, C → cy E → aA
W 2 = {A, C, E} U {S} de la regla S → AC
W 3 = {A, C, E, S} U ∅
Dado que W 2 = W 3 , podemos derivar G 'como -
G '= {{A, C, E, S}, {a, c, e}, P, {S}}
donde P: S → AC, A → a, C → c, E → aA | mi
Phase 2 -
Y 1 = {S}
Y 2 = {S, A, C} de la regla S → AC
Y 3 = {S, A, C, a, c} de las reglas A → a y C → c
Y 4 = {S, A, C, a, c}
Como Y 3 = Y 4 , podemos derivar G ”como -
G ”= {{A, C, S}, {a, c}, P, {S}}
donde P: S → AC, A → a, C → c
Eliminación de unidades de producción
Cualquier regla de producción en la forma A → B donde A, B ∈ No terminal se llama unit production..
Procedimiento de remoción -
Step 1 - Para eliminar A → B, agregar producción A → x a la regla gramatical siempre que B → xocurre en la gramática. [x ∈ Terminal, x puede ser nulo]
Step 2 - eliminar A → B de la gramática.
Step 3 - Repita desde el paso 1 hasta eliminar todas las unidades de producción.
Problem
Elimine la producción unitaria de lo siguiente:
S → XY, X → a, Y → Z | b, Z → M, M → N, N → a
Solution -
Hay 3 unidades de producción en la gramática:
Y → Z, Z → M y M → N
At first, we will remove M → N.
Como N → a, agregamos M → a, y M → N se elimina.
El conjunto de producción se convierte
S → XY, X → a, Y → Z | b, Z → M, M → a, N → a
Now we will remove Z → M.
Como M → a, agregamos Z → a, y Z → M se elimina.
El conjunto de producción se convierte
S → XY, X → a, Y → Z | b, Z → a, M → a, N → a
Now we will remove Y → Z.
Como Z → a, agregamos Y → a, y Y → Z se elimina.
El conjunto de producción se convierte
S → XY, X → a, Y → a | b, Z → a, M → a, N → a
Ahora Z, M y N son inalcanzables, por lo tanto, podemos eliminarlos.
El CFG final está libre de producción unitaria -
S → XY, X → a, Y → a | segundo
Eliminación de producciones nulas
En un CFG, un símbolo no terminal ‘A’ es una variable que acepta valores NULL si hay una producción A → ε o hay una derivación que comienza en A y finalmente termina con
ε: A → .......… → ε
Procedimiento de remoción
Step 1 - Descubra las variables no terminales que aceptan valores NULL que derivan ε.
Step 2 - Para cada producción A → a, construye todas las producciones A → x dónde x se obtiene de ‘a’ quitando uno o varios no terminales del Paso 1.
Step 3 - Combinar las producciones originales con el resultado del paso 2 y eliminar ε - productions.
Problem
Elimine la producción nula de lo siguiente:
S → ASA | aB | b, A → B, B → b | ∈
Solution -
Hay dos variables que aceptan valores NULL: A y B
At first, we will remove B → ε.
Después de quitar B → ε, el conjunto de producción se convierte en -
S → ASA | aB | b | a, A ε B | b | & épsilon, B → b
Now we will remove A → ε.
Después de quitar A → ε, el conjunto de producción se convierte en -
S → ASA | aB | b | a | SA | AS | S, A → B | b, B → b
Este es el conjunto de producción final sin transición nula.
Un CFG está en la forma normal de Chomsky si las producciones están en las siguientes formas:
- A → a
- A → BC
- S → ε
donde A, B y C son no terminales y a es terminal.
Algoritmo para convertir en forma normal de Chomsky -
Step 1 - Si el símbolo de inicio S ocurre en algún lado derecho, crea un nuevo símbolo de inicio S’ y una nueva producción S’→ S.
Step 2- Eliminar producciones nulas. (Usando el algoritmo de eliminación de producción nula que se discutió anteriormente)
Step 3- Eliminar producciones unitarias. (Usando el algoritmo de eliminación de producción de unidades discutido anteriormente)
Step 4 - Reemplazar cada producción A → B1…Bn dónde n > 2 con A → B1C dónde C → B2 …Bn. Repita este paso para todas las producciones que tengan dos o más símbolos en el lado derecho.
Step 5 - Si el lado derecho de alguna producción está en el formulario A → aB donde a es una terminal y A, B son no terminales, entonces la producción se reemplaza por A → XB y X → a. Repita este paso para cada producción que tenga el formularioA → aB.
Problema
Convierta el siguiente CFG en CNF
S → ASA | aB, A → B | S, B → b | ε
Solución
(1) Ya que S aparece en RHS, agregamos un nuevo estado S0 y S0→S se agrega al conjunto de producción y se convierte en -
S 0 → S, S → ASA | aB, A → B | S, B → b | ∈
(2) Ahora eliminaremos las producciones nulas -
B → ∈ y A → ∈
Después de eliminar B → ε, el conjunto de producción se convierte en -
S 0 → S, S → ASA | aB | a, A → B | S | ∈, B → b
Después de eliminar A → ∈, el conjunto de producción se convierte en -
S 0 → S, S → ASA | aB | a | AS | SA | S, A → B | S, B → b
(3) Ahora eliminaremos las producciones unitarias.
Después de eliminar S → S, el conjunto de producción se convierte en -
S 0 → S, S → ASA | aB | a | AS | SA, A → B | S, B → b
Después de eliminar S 0 → S, el conjunto de producción se convierte en -
S 0 → ASA | aB | a | AS | SA, S → ASA | aB | a | AS | SA
A → B | S, B → b
Después de eliminar A → B, el conjunto de producción se convierte en -
S 0 → ASA | aB | a | AS | SA, S → ASA | aB | a | AS | SA
A → S | segundo
B → b
Después de eliminar A → S, el conjunto de producción se convierte en -
S 0 → ASA | aB | a | AS | SA, S → ASA | aB | a | AS | SA
A → b | ASA | aB | a | AS | SA, B → b
(4) Ahora encontraremos más de dos variables en el RHS
Aquí, S 0 → ASA, S → ASA, A → ASA viola dos no terminales en RHS
Por lo tanto, aplicaremos el paso 4 y el paso 5 para obtener el siguiente conjunto de producción final que está en CNF:
S 0 → AX | aB | a | AS | SA
S → AX | aB | a | AS | SA
A → b | AX | aB | a | AS | SA
B → b
X → SA
(5)Tenemos que cambiar las producciones S 0 → aB, S → aB, A → aB
Y el conjunto de producción final se convierte en ...
S 0 → AX | YB | a | AS | SA
S → AX | YB | a | AS | SA
A → b A → b | AX | YB | a | AS | SA
B → b
X → SA
Y → a
Un CFG está en la forma normal de Greibach si las producciones están en las siguientes formas:
A → b
A → bD 1 … D n
S → ε
donde A, D 1 , ...., D n son no terminales y b es un terminal.
Algoritmo para convertir un CFG en forma normal de Greibach
Step 1 - Si el símbolo de inicio S ocurre en algún lado derecho, crea un nuevo símbolo de inicio S’ y una nueva producción S’ → S.
Step 2- Eliminar producciones nulas. (Usando el algoritmo de eliminación de producción nula que se discutió anteriormente)
Step 3- Eliminar producciones unitarias. (Usando el algoritmo de eliminación de producción de unidades discutido anteriormente)
Step 4 - Eliminar todas las recursiones por la izquierda directas e indirectas.
Step 5 - Hacer sustituciones adecuadas de producciones para convertirlo en la forma adecuada de GNF.
Problema
Convierta el siguiente CFG en CNF
S → XY | Xn | pags
X → mX | metro
Y → Xn | o
Solución
Aquí, Sno aparece en el lado derecho de ninguna producción y no hay unidades o producciones nulas en el conjunto de reglas de producción. Entonces, podemos saltarnos del Paso 1 al Paso 3.
Step 4
Ahora, después de reemplazar
X en S → XY | Xo | pags
con
mX | metro
obtenemos
S → mXY | mY | mXo | mo | pags.
Y después de reemplazar
X en Y → X n | o
con el lado derecho de
X → mX | metro
obtenemos
Y → mXn | mn | o.
Se agregan dos nuevas producciones O → o y P → p al conjunto de producción y luego llegamos al GNF final de la siguiente manera:
S → mXY | mY | mXC | mC | pags
X → mX | metro
Y → mXD | mD | o
O → o
P → p
Lema
Si L es un lenguaje libre de contexto, hay una duración de bombeo p tal que cualquier cuerda w ∈ L de longitud ≥ p Se puede escribir como w = uvxyz, dónde vy ≠ ε, |vxy| ≤ py para todos i ≥ 0, uvixyiz ∈ L.
Aplicaciones de la lema de bombeo
El lema de bombeo se utiliza para comprobar si una gramática está libre de contexto o no. Tomemos un ejemplo y mostremos cómo se verifica.
Problema
Descubra si el idioma L = {xnynzn | n ≥ 1} es libre de contexto o no.
Solución
Dejar Les libre de contexto. Luego,L debe satisfacer el lema de bombeo.
Primero, elige un número ndel lema de bombeo. Luego, toma z como 0 n 1 n 2 n .
Romper z dentro uvwxy, dónde
|vwx| ≤ n and vx ≠ ε.
Por lo tanto vwxno puede involucrar 0 y 2, ya que el último 0 y los primeros 2 están separados por al menos (n + 1) posiciones. Hay dos casos:
Case 1 - vwxno tiene 2. Luegovxtiene solo 0 y 1. Luegouwy, que tendría que estar en L, tiene n 2 s, pero menos de n 0 o 1.
Case 2 - vwx no tiene ceros.
Aquí ocurre la contradicción.
Por lo tanto, L no es un lenguaje libre de contexto.
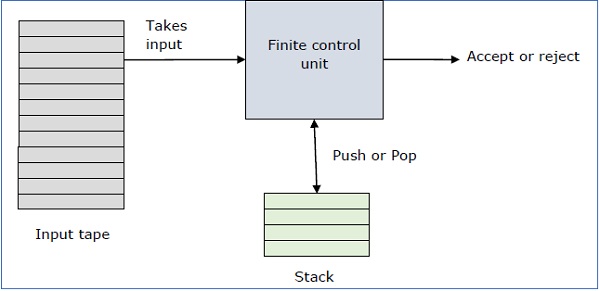
Estructura básica de PDA
Un autómata pushdown es una forma de implementar una gramática libre de contexto de una manera similar a la que diseñamos DFA para una gramática regular. Un DFA puede recordar una cantidad finita de información, pero un PDA puede recordar una cantidad infinita de información.
Básicamente, un autómata pushdown es ...
"Finite state machine" + "a stack"
Un autómata de empuje tiene tres componentes:
- una cinta de entrada,
- una unidad de control, y
- una pila de tamaño infinito.
El cabezal de la pila escanea el símbolo superior de la pila.
Una pila hace dos operaciones:
Push - se agrega un nuevo símbolo en la parte superior.
Pop - el símbolo superior se lee y se elimina.
Una PDA puede leer o no un símbolo de entrada, pero tiene que leer la parte superior de la pila en cada transición.
Una PDA se puede describir formalmente como una tupla de 7 (Q, ∑, S, δ, q 0 , I, F) -
Q es el número finito de estados
∑ es el alfabeto de entrada
S son símbolos de pila
δ es la función de transición: Q × (∑ ∪ {ε}) × S × Q × S *
q0es el estado inicial (q 0 ∈ Q)
I es el símbolo inicial de la parte superior de la pila (I ∈ S)
F es un conjunto de estados de aceptación (F ∈ Q)
El siguiente diagrama muestra una transición en un PDA de un estado q 1 al estado q 2 , etiquetado como a, b → c -

Esto significa en el estado q1, si encontramos una cadena de entrada ‘a’ y el símbolo superior de la pila es ‘b’, luego hacemos estallar ‘b’, empujar ‘c’ en la parte superior de la pila y pasar al estado q2.
Terminologías relacionadas con PDA
Descripción instantánea
La descripción instantánea (ID) de un PDA está representada por un triplete (q, w, s) donde
q es el estado
w es entrada no consumida
s es el contenido de la pila
Notación de torniquete
La notación "torniquete" se utiliza para conectar pares de ID que representan uno o varios movimientos de una PDA. El proceso de transición se indica con el símbolo del torniquete "⊢".
Considere un PDA (Q, ∑, S, δ, q 0 , I, F). Una transición se puede representar matemáticamente mediante la siguiente notación de torniquete:
(p, aw, Tβ) ⊢ (q, w, αb)Esto implica que mientras se realiza una transición de estado p a estado q, el símbolo de entrada ‘a’ se consume, y la parte superior de la pila ‘T’ es reemplazado por una nueva cadena ‘α’.
Note - Si queremos cero o más movimientos de una PDA, tenemos que usar el símbolo (⊢ *) para ello.
Hay dos formas diferentes de definir la aceptabilidad de PDA.
Aceptabilidad final del estado
En la aceptabilidad del estado final, una PDA acepta una cadena cuando, después de leer la cadena completa, la PDA está en un estado final. Desde el estado inicial, podemos hacer movimientos que terminen en un estado final con cualquier valor de pila. Los valores de la pila son irrelevantes siempre que terminemos en un estado final.
Para un PDA (Q, ∑, S, δ, q 0 , I, F), el lenguaje aceptado por el conjunto de estados finales F es -
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, x), q ∈ F}
para cualquier cadena de pila de entrada x.
Aceptabilidad de pila vacía
Aquí una PDA acepta una cadena cuando, después de leer la cadena completa, la PDA ha vaciado su pila.
Para un PDA (Q, ∑, S, δ, q 0 , I, F), el lenguaje aceptado por la pila vacía es -
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, ε), q ∈ Q}
Ejemplo
Construya una PDA que acepte L = {0n 1n | n ≥ 0}
Solución

Este idioma acepta L = {ε, 01, 0011, 000111, .............................}
Aquí, en este ejemplo, el número de ‘a’ y ‘b’ tiene que ser el mismo.
Inicialmente ponemos un símbolo especial ‘$’ en la pila vacía.
Entonces en el estado q2, si encontramos la entrada 0 y top es Null, empujamos 0 a la pila. Esto puede repetirse. Y si encontramos la entrada 1 y la parte superior es 0, sacamos este 0.
Entonces en el estado q3, si encontramos la entrada 1 y la parte superior es 0, sacamos este 0. Esto también puede iterar. Y si encontramos la entrada 1 y top es 0, sacamos el elemento superior.
Si el símbolo especial '$' se encuentra en la parte superior de la pila, se abre y finalmente pasa al estado de aceptación q 4 .
Ejemplo
Construya una PDA que acepte L = {ww R | w = (a + b) *}
Solution

Inicialmente colocamos un símbolo especial '$' en la pila vacía. En el estadoq2, la wse está leyendo. En el estadoq3, cada 0 o 1 aparece cuando coincide con la entrada. Si se proporciona cualquier otra entrada, la PDA pasará a un estado inactivo. Cuando llegamos a ese símbolo especial '$', vamos al estado de aceptaciónq4.
Si una gramática G es libre de contexto, podemos construir un PDA no determinista equivalente que acepte el lenguaje producido por la gramática libre de contexto G. Se puede construir un analizador para la gramáticaG.
También si P es un autómata pushdown, se puede construir una gramática libre de contexto equivalente G donde
L(G) = L(P)
En los siguientes dos temas, discutiremos cómo convertir de PDA a CFG y viceversa.
Algoritmo para encontrar PDA correspondiente a un CFG dado
Input - Un CFG, G = (V, T, P, S)
Output- PDA equivalente, P = (Q, ∑, S, δ, q 0 , I, F)
Step 1 - Convertir las producciones del CFG en GNF.
Step 2 - La PDA tendrá un solo estado {q}.
Step 3 - El símbolo de inicio de CFG será el símbolo de inicio en la PDA.
Step 4 - Todos los no terminales del CFG serán los símbolos de pila del PDA y todos los terminales del CFG serán los símbolos de entrada del PDA.
Step 5 - Para cada producción en forma A → aX donde a es terminal y A, X son una combinación de terminales y no terminales, haga una transición δ (q, a, A).
Problema
Construya un PDA a partir del siguiente CFG.
G = ({S, X}, {a, b}, P, S)
donde están las producciones -
S → XS | ε , A → aXb | Ab | ab
Solución
Deje que el PDA equivalente,
P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)
donde δ -
δ (q, ε, S) = {(q, XS), (q, ε)}
δ (q, ε, X) = {(q, aXb), (q, Xb), (q, ab)}
δ (q, a, a) = {(q, ε)}
δ (q, 1, 1) = {(q, ε)}
Algoritmo para encontrar CFG correspondiente a un PDA dado
Input - Un CFG, G = (V, T, P, S)
Output- PDA equivalente, P = (Q, ∑, S, δ, q 0 , I, F) tal que los no terminales de la gramática G serán {X wx | w, x ∈ Q} y el estado de inicio será un q0, F .
Step 1- Para cada w, x, y, z ∈ Q, m ∈ S y a, b ∈ ∑, si δ (w, a, ε) contiene (y, m) y (z, b, m) contiene (x, ε), agregue la regla de producción X wx → a X yz b en la gramática G.
Step 2- Para cada w, x, y, z ∈ Q, agregue la regla de producción X wx → X wy X yx en la gramática G.
Step 3- Para w ∈ Q, agregue la regla de producción X ww → ε en la gramática G.
El análisis se usa para derivar una cadena usando las reglas de producción de una gramática. Se utiliza para comprobar la aceptabilidad de una cadena. El compilador se utiliza para comprobar si una cadena es sintácticamente correcta o no. Un analizador toma las entradas y crea un árbol de análisis.
Un analizador puede ser de dos tipos:
Top-Down Parser - El análisis de arriba hacia abajo comienza desde arriba con el símbolo de inicio y deriva una cadena usando un árbol de análisis.
Bottom-Up Parser - El análisis de abajo hacia arriba comienza desde abajo con la cadena y llega al símbolo de inicio usando un árbol de análisis.
Diseño de analizador de arriba hacia abajo
Para el análisis de arriba hacia abajo, una PDA tiene los siguientes cuatro tipos de transiciones:
Haga estallar el no terminal en el lado izquierdo de la producción en la parte superior de la pila y empuje su cuerda del lado derecho.
Si el símbolo superior de la pila coincide con el símbolo de entrada que se está leyendo, páselo.
Empuje el símbolo de inicio 'S' en la pila.
Si la cadena de entrada se lee por completo y la pila está vacía, vaya al estado final 'F'.
Ejemplo
Diseñe un analizador de arriba hacia abajo para la expresión "x + y * z" para la gramática G con las siguientes reglas de producción:
P: S → S + X | X, X → X * Y | Y, Y → (S) | carné de identidad
Solution
Si el PDA es (Q, ∑, S, δ, q 0 , I, F), entonces el análisis sintáctico descendente es -
(x + y * z, I) ⊢ (x + y * z, SI) ⊢ (x + y * z, S + XI) ⊢ (x + y * z, X + XI)
⊢ (x + y * z, Y + XI) ⊢ (x + y * z, x + XI) ⊢ (+ y * z, + XI) ⊢ (y * z, XI)
⊢ (y * z, X * YI) ⊢ (y * z, y * YI) ⊢ (* z, * YI) ⊢ (z, YI) ⊢ (z, zI) ⊢ (ε, I)
Diseño de un analizador ascendente
Para el análisis de abajo hacia arriba, una PDA tiene los siguientes cuatro tipos de transiciones:
Empuje el símbolo de entrada actual en la pila.
Reemplace el lado derecho de una producción en la parte superior de la pila con su lado izquierdo.
Si la parte superior del elemento de la pila coincide con el símbolo de entrada actual, sáquelo.
Si la cadena de entrada se lee por completo y solo si el símbolo de inicio 'S' permanece en la pila, páselo y vaya al estado final 'F'.
Ejemplo
Diseñe un analizador de arriba hacia abajo para la expresión "x + y * z" para la gramática G con las siguientes reglas de producción:
P: S → S + X | X, X → X * Y | Y, Y → (S) | carné de identidad
Solution
Si el PDA es (Q, ∑, S, δ, q 0 , I, F), entonces el análisis sintáctico ascendente es -
(x + y * z, I) ⊢ (+ y * z, xI) ⊢ (+ y * z, YI) ⊢ (+ y * z, XI) ⊢ (+ y * z, SI)
⊢ (y * z, + SI) ⊢ (* z, y + SI) ⊢ (* z, Y + SI) ⊢ (* z, X + SI) ⊢ (z, * X + SI)
⊢ (ε, z * X + SI) ⊢ (ε, Y * X + SI) ⊢ (ε, X + SI) ⊢ (ε, SI)
Una máquina de Turing es un dispositivo de aceptación que acepta los idiomas (conjunto enumerable recursivamente) generados por gramáticas de tipo 0. Fue inventado en 1936 por Alan Turing.
Definición
Una máquina de Turing (TM) es un modelo matemático que consiste en una cinta de longitud infinita dividida en celdas en las que se da entrada. Consiste en un cabezal que lee la cinta de entrada. Un registro estatal almacena el estado de la máquina de Turing. Después de leer un símbolo de entrada, se reemplaza con otro símbolo, se cambia su estado interno y se mueve de una celda a la derecha o la izquierda. Si la TM alcanza el estado final, se acepta la cadena de entrada, de lo contrario se rechaza.
Una TM se puede describir formalmente como una tupla de 7 (Q, X, ∑, δ, q 0 , B, F) donde -
Q es un conjunto finito de estados
X es el alfabeto de la cinta
∑ es el alfabeto de entrada
δes una función de transición; δ: Q × X → Q × X × {Left_shift, Right_shift}.
q0 es el estado inicial
B es el símbolo en blanco
F es el conjunto de estados finales
Comparación con el autómata anterior
La siguiente tabla muestra una comparación de cómo una máquina de Turing se diferencia de Finite Automaton y Pushdown Automaton.
| Máquina | Estructura de datos de pila | Determinista? |
|---|---|---|
| Autómata finito | N / A | si |
| Autómata de empuje | Último en entrar, primero en salir (LIFO) | No |
| Máquina de Turing | Cinta infinita | si |
Ejemplo de máquina de Turing
Máquina de Turing M = (Q, X, ∑, δ, q 0 , B, F) con
- Q = {q 0 , q 1 , q 2 , q f }
- X = {a, b}
- ∑ = {1}
- q 0 = {q 0 }
- B = símbolo en blanco
- F = {q f }
δ está dado por -
| Símbolo del alfabeto de cinta | Estado actual 'q 0 ' | Estado actual 'q 1 ' | Estado actual 'q 2 ' |
|---|---|---|---|
| un | 1Rq 1 | 1Lq 0 | 1Lq f |
| segundo | 1Lq 2 | 1Rq 1 | 1Rq f |
Aquí la transición 1Rq 1 implica que el símbolo de escritura es 1, la cinta se mueve hacia la derecha y el siguiente estado es q 1 . De manera similar, la transición 1Lq 2 implica que el símbolo de escritura es 1, la cinta se mueve hacia la izquierda y el siguiente estado es q 2 .
Complejidad temporal y espacial de una máquina de Turing
Para una máquina de Turing, la complejidad del tiempo se refiere a la medida del número de veces que se mueve la cinta cuando la máquina se inicializa para algunos símbolos de entrada y la complejidad del espacio es el número de celdas de la cinta escritas.
Complejidad temporal todas las funciones razonables -
T(n) = O(n log n)
Complejidad espacial de TM -
S(n) = O(n)
Una TM acepta un idioma si entra en un estado final para cualquier cadena de entrada w. Un idioma es enumerable de forma recursiva (generado por la gramática de tipo 0) si es aceptado por una máquina de Turing.
Una TM decide un idioma si lo acepta y entra en un estado de rechazo para cualquier entrada que no esté en el idioma. Un idioma es recursivo si lo decide una máquina de Turing.
Puede haber algunos casos en los que una MT no se detenga. Tal MT acepta el idioma, pero no lo decide.
Diseñar una máquina de Turing
Las pautas básicas para diseñar una máquina de Turing se explican a continuación con la ayuda de un par de ejemplos.
Ejemplo 1
Diseñe una TM para reconocer todas las cadenas que constan de un número impar de α.
Solution
La máquina de Turing M se puede construir mediante los siguientes movimientos:
Dejar q1 ser el estado inicial.
Si M es en q1; al escanear α, entra en el estadoq2 y escribe B (blanco).
Si M es en q2; al escanear α, entra en el estadoq1 y escribe B (blanco).
De los movimientos anteriores, podemos ver que M entra al estado q1 si escanea un número par de α, y entra en el estado q2si escanea un número impar de α. Por lo tantoq2 es el único estado que acepta.
Por lo tanto,
M = {{q 1 , q 2 }, {1}, {1, B}, δ, q 1 , B, {q 2 }}
donde δ está dado por -
| Símbolo del alfabeto de cinta | Estado actual 'q 1 ' | Present State ‘q2’ |
|---|---|---|
| α | BRq2 | BRq1 |
Example 2
Design a Turing Machine that reads a string representing a binary number and erases all leading 0’s in the string. However, if the string comprises of only 0’s, it keeps one 0.
Solution
Let us assume that the input string is terminated by a blank symbol, B, at each end of the string.
The Turing Machine, M, can be constructed by the following moves −
Let q0 be the initial state.
If M is in q0, on reading 0, it moves right, enters the state q1 and erases 0. On reading 1, it enters the state q2 and moves right.
If M is in q1, on reading 0, it moves right and erases 0, i.e., it replaces 0’s by B’s. On reaching the leftmost 1, it enters q2 and moves right. If it reaches B, i.e., the string comprises of only 0’s, it moves left and enters the state q3.
If M is in q2, on reading either 0 or 1, it moves right. On reaching B, it moves left and enters the state q4. This validates that the string comprises only of 0’s and 1’s.
If M is in q3, it replaces B by 0, moves left and reaches the final state qf.
If M is in q4, on reading either 0 or 1, it moves left. On reaching the beginning of the string, i.e., when it reads B, it reaches the final state qf.
Hence,
M = {{q0, q1, q2, q3, q4, qf}, {0,1, B}, {1, B}, δ, q0, B, {qf}}
where δ is given by −
| Tape alphabet symbol | Present State ‘q0’ | Present State ‘q1’ | Present State ‘q2’ | Present State ‘q3’ | Present State ‘q4’ |
|---|---|---|---|---|---|
| 0 | BRq1 | BRq1 | ORq2 | - | OLq4 |
| 1 | 1Rq2 | 1Rq2 | 1Rq2 | - | 1Lq4 |
| B | BRq1 | BLq3 | BLq4 | OLqf | BRqf |
Multi-tape Turing Machines have multiple tapes where each tape is accessed with a separate head. Each head can move independently of the other heads. Initially the input is on tape 1 and others are blank. At first, the first tape is occupied by the input and the other tapes are kept blank. Next, the machine reads consecutive symbols under its heads and the TM prints a symbol on each tape and moves its heads.

A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −
Q is a finite set of states
X is the tape alphabet
B is the blank symbol
δ is a relation on states and symbols where
δ: Q × Xk → Q × (X × {Left_shift, Right_shift, No_shift })k
where there is k number of tapes
q0 is the initial state
F is the set of final states
Note − Every Multi-tape Turing machine has an equivalent single-tape Turing machine.
Multi-track Turing machines, a specific type of Multi-tape Turing machine, contain multiple tracks but just one tape head reads and writes on all tracks. Here, a single tape head reads n symbols from n tracks at one step. It accepts recursively enumerable languages like a normal single-track single-tape Turing Machine accepts.
A Multi-track Turing machine can be formally described as a 6-tuple (Q, X, ∑, δ, q0, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a relation on states and symbols where
δ(Qi, [a1, a2, a3,....]) = (Qj, [b1, b2, b3,....], Left_shift or Right_shift)
q0 is the initial state
F is the set of final states
Note − For every single-track Turing Machine S, there is an equivalent multi-track Turing Machine M such that L(S) = L(M).
In a Non-Deterministic Turing Machine, for every state and symbol, there are a group of actions the TM can have. So, here the transitions are not deterministic. The computation of a non-deterministic Turing Machine is a tree of configurations that can be reached from the start configuration.
An input is accepted if there is at least one node of the tree which is an accept configuration, otherwise it is not accepted. If all branches of the computational tree halt on all inputs, the non-deterministic Turing Machine is called a Decider and if for some input, all branches are rejected, the input is also rejected.
A non-deterministic Turing machine can be formally defined as a 6-tuple (Q, X, ∑, δ, q0, B, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
δ is a transition function;
δ : Q × X → P(Q × X × {Left_shift, Right_shift}).
q0 is the initial state
B is the blank symbol
F is the set of final states
A Turing Machine with a semi-infinite tape has a left end but no right end. The left end is limited with an end marker.

It is a two-track tape −
Upper track − It represents the cells to the right of the initial head position.
Lower track − It represents the cells to the left of the initial head position in reverse order.
The infinite length input string is initially written on the tape in contiguous tape cells.
The machine starts from the initial state q0 and the head scans from the left end marker ‘End’. In each step, it reads the symbol on the tape under its head. It writes a new symbol on that tape cell and then it moves the head either into left or right one tape cell. A transition function determines the actions to be taken.
It has two special states called accept state and reject state. If at any point of time it enters into the accepted state, the input is accepted and if it enters into the reject state, the input is rejected by the TM. In some cases, it continues to run infinitely without being accepted or rejected for some certain input symbols.
Note − Turing machines with semi-infinite tape are equivalent to standard Turing machines.
A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some bounded finite length.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The computation is restricted to the constant bounded area. The input alphabet contains two special symbols which serve as left end markers and right end markers which mean the transitions neither move to the left of the left end marker nor to the right of the right end marker of the tape.
A linear bounded automaton can be defined as an 8-tuple (Q, X, ∑, q0, ML, MR, δ, F) where −
Q is a finite set of states
X is the tape alphabet
∑ is the input alphabet
q0 is the initial state
ML is the left end marker
MR is the right end marker where MR ≠ ML
δ is a transition function which maps each pair (state, tape symbol) to (state, tape symbol, Constant ‘c’) where c can be 0 or +1 or -1
F is the set of final states

A deterministic linear bounded automaton is always context-sensitive and the linear bounded automaton with empty language is undecidable..
A language is called Decidable or Recursive if there is a Turing machine which accepts and halts on every input string w. Every decidable language is Turing-Acceptable.

A decision problem P is decidable if the language L of all yes instances to P is decidable.
For a decidable language, for each input string, the TM halts either at the accept or the reject state as depicted in the following diagram −

Example 1
Find out whether the following problem is decidable or not −
Is a number ‘m’ prime?
Solution
Prime numbers = {2, 3, 5, 7, 11, 13, …………..}
Divide the number ‘m’ by all the numbers between ‘2’ and ‘√m’ starting from ‘2’.
If any of these numbers produce a remainder zero, then it goes to the “Rejected state”, otherwise it goes to the “Accepted state”. So, here the answer could be made by ‘Yes’ or ‘No’.
Hence, it is a decidable problem.
Example 2
Given a regular language L and string w, how can we check if w ∈ L?
Solution
Take the DFA that accepts L and check if w is accepted

Some more decidable problems are −
- Does DFA accept the empty language?
- Is L1 ∩ L2 = ∅ for regular sets?
Note −
If a language L is decidable, then its complement L' is also decidable
If a language is decidable, then there is an enumerator for it.
For an undecidable language, there is no Turing Machine which accepts the language and makes a decision for every input string w (TM can make decision for some input string though). A decision problem P is called “undecidable” if the language L of all yes instances to P is not decidable. Undecidable languages are not recursive languages, but sometimes, they may be recursively enumerable languages.

Example
- The halting problem of Turing machine
- The mortality problem
- The mortal matrix problem
- The Post correspondence problem, etc.
Input − A Turing machine and an input string w.
Problem − Does the Turing machine finish computing of the string w in a finite number of steps? The answer must be either yes or no.
Proof − At first, we will assume that such a Turing machine exists to solve this problem and then we will show it is contradicting itself. We will call this Turing machine as a Halting machine that produces a ‘yes’ or ‘no’ in a finite amount of time. If the halting machine finishes in a finite amount of time, the output comes as ‘yes’, otherwise as ‘no’. The following is the block diagram of a Halting machine −

Now we will design an inverted halting machine (HM)’ as −
If H returns YES, then loop forever.
If H returns NO, then halt.
The following is the block diagram of an ‘Inverted halting machine’ −

Further, a machine (HM)2 which input itself is constructed as follows −
- If (HM)2 halts on input, loop forever.
- Else, halt.
Here, we have got a contradiction. Hence, the halting problem is undecidable.
Rice theorem states that any non-trivial semantic property of a language which is recognized by a Turing machine is undecidable. A property, P, is the language of all Turing machines that satisfy that property.
Formal Definition
If P is a non-trivial property, and the language holding the property, Lp , is recognized by Turing machine M, then Lp = {<M> | L(M) ∈ P} is undecidable.
Description and Properties
Property of languages, P, is simply a set of languages. If any language belongs to P (L ∈ P), it is said that L satisfies the property P.
A property is called to be trivial if either it is not satisfied by any recursively enumerable languages, or if it is satisfied by all recursively enumerable languages.
A non-trivial property is satisfied by some recursively enumerable languages and are not satisfied by others. Formally speaking, in a non-trivial property, where L ∈ P, both the following properties hold:
Property 1 − There exists Turing Machines, M1 and M2 that recognize the same language, i.e. either ( <M1>, <M2> ∈ L ) or ( <M1>,<M2> ∉ L )
Property 2 − There exists Turing Machines M1 and M2, where M1 recognizes the language while M2 does not, i.e. <M1> ∈ L and <M2> ∉ L
Proof
Suppose, a property P is non-trivial and φ ∈ P.
Since, P is non-trivial, at least one language satisfies P, i.e., L(M0) ∈ P , ∋ Turing Machine M0.
Let, w be an input in a particular instant and N is a Turing Machine which follows −
On input x
- Run M on w
- If M does not accept (or doesn't halt), then do not accept x (or do not halt)
- If M accepts w then run M0 on x. If M0 accepts x, then accept x.
A function that maps an instance ATM = {<M,w>| M accepts input w} to a N such that
- If M accepts w and N accepts the same language as M0, Then L(M) = L(M0) ∈ p
- If M does not accept w and N accepts φ, Then L(N) = φ ∉ p
Since ATM is undecidable and it can be reduced to Lp, Lp is also undecidable.
The Post Correspondence Problem (PCP), introduced by Emil Post in 1946, is an undecidable decision problem. The PCP problem over an alphabet ∑ is stated as follows −
Given the following two lists, M and N of non-empty strings over ∑ −
M = (x1, x2, x3,………, xn)
N = (y1, y2, y3,………, yn)
We can say that there is a Post Correspondence Solution, if for some i1,i2,………… ik, where 1 ≤ ij ≤ n, the condition xi1 …….xik = yi1 …….yik satisfies.
Example 1
Find whether the lists
M = (abb, aa, aaa) and N = (bba, aaa, aa)
have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | Abb | aa | aaa |
| N | Bba | aaa | aa |
Here,
x2x1x3 = ‘aaabbaaa’
and y2y1y3 = ‘aaabbaaa’
We can see that
x2x1x3 = y2y1y3
Hence, the solution is i = 2, j = 1, and k = 3.
Example 2
Find whether the lists M = (ab, bab, bbaaa) and N = (a, ba, bab) have a Post Correspondence Solution?
Solution
| x1 | x2 | x3 | |
|---|---|---|---|
| M | ab | bab | bbaaa |
| N | a | ba | bab |
In this case, there is no solution because −
| x2x1x3 | ≠ | y2y1y3 | (Lengths are not same)
Hence, it can be said that this Post Correspondence Problem is undecidable.