Minimización de DFA
Minimización de DFA mediante el teorema de Myphill-Nerode
Algoritmo
Input - DFA
Output - DFA minimizado
Step 1- Dibuje una tabla para todos los pares de estados (Q i , Q j ) no necesariamente conectados directamente [Todos están sin marcar inicialmente]
Step 2- Considere cada par de estados (Q i , Q j ) en el DFA donde Q i ∈ F y Q j ∉ F o viceversa y márquelos. [Aquí F es el conjunto de estados finales]
Step 3 - Repita este paso hasta que no podamos marcar más estados -
Si hay un par sin marcar (Q i , Q j ), márquelo si el par {δ (Q i , A), δ (Q i , A)} está marcado para algún alfabeto de entrada.
Step 4- Combinar todos los pares sin marcar (Q i , Q j ) y convertirlos en un solo estado en el DFA reducido.
Ejemplo
Usemos el algoritmo 2 para minimizar el DFA que se muestra a continuación.

Step 1 - Dibujamos una tabla para todos los pares de estados.
| una | segundo | C | re | mi | F | |
| una | ||||||
| segundo | ||||||
| C | ||||||
| re | ||||||
| mi | ||||||
| F |
Step 2 - Marcamos los pares de estados.
| una | segundo | C | re | mi | F | |
| una | ||||||
| segundo | ||||||
| C | ✔ | ✔ | ||||
| re | ✔ | ✔ | ||||
| mi | ✔ | ✔ | ||||
| F | ✔ | ✔ | ✔ |
Step 3- Intentaremos marcar los pares de estados, con una marca de verificación de color verde, de forma transitiva. Si ingresamos 1 para indicar 'a' y 'f', irá al estado 'c' y 'f' respectivamente. (c, f) ya está marcado, por lo tanto marcaremos el par (a, f). Ahora, ingresamos 1 para indicar 'b' y 'f'; irá al estado 'd' y 'f' respectivamente. (d, f) ya está marcado, por lo que marcaremos el par (b, f).
| una | segundo | C | re | mi | F | |
| una | ||||||
| segundo | ||||||
| C | ✔ | ✔ | ||||
| re | ✔ | ✔ | ||||
| mi | ✔ | ✔ | ||||
| F | ✔ | ✔ | ✔ | ✔ | ✔ |
Después del paso 3, tenemos combinaciones de estados {a, b} {c, d} {c, e} {d, e} que no están marcadas.
Podemos recombinar {c, d} {c, e} {d, e} en {c, d, e}
Por lo tanto, obtuvimos dos estados combinados como - {a, b} y {c, d, e}
Por tanto, el DFA minimizado final contendrá tres estados {f}, {a, b} y {c, d, e}
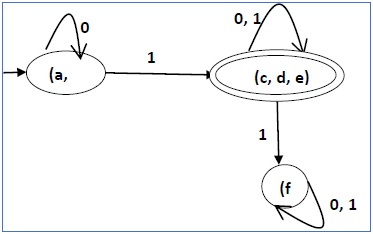
Minimización de DFA mediante el teorema de equivalencia
Si X e Y son dos estados en un DFA, podemos combinar estos dos estados en {X, Y} si no se pueden distinguir. Se pueden distinguir dos estados, si hay al menos una cadena S, de modo que uno de δ (X, S) y δ (Y, S) acepta y otro no acepta. Por lo tanto, un DFA es mínimo si y solo si todos los estados son distinguibles.
Algoritmo 3
Step 1 - Todos los estados Q están divididos en dos particiones - final states y non-final states y se denotan por P0. Todos los estados de una partición son 0º equivalentes. Tomar un contadork e inicializarlo con 0.
Step 2- Incrementar k en 1. Para cada partición en P k , divida los estados en P k en dos particiones si son k-distinguibles. Dos estados dentro de esta partición X e Y son k-distinguibles si hay una entradaS tal que δ(X, S) y δ(Y, S) son (k-1) -distinguible.
Step 3- Si P k ≠ P k-1 , repita el paso 2; de lo contrario, vaya al paso 4.
Step 4- Combinar k- ésimo conjuntos equivalentes y convertirlos en los nuevos estados del DFA reducido.
Ejemplo
Consideremos el siguiente DFA:

| q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| una | segundo | C |
| segundo | una | re |
| C | mi | F |
| re | mi | F |
| mi | mi | F |
| F | F | F |
Apliquemos el algoritmo anterior al DFA anterior:
- P 0 = {(c, d, e), (a, b, f)}
- P 1 = {(c, d, e), (a, b), (f)}
- P 2 = {(c, d, e), (a, b), (f)}
Por tanto, P 1 = P 2 .
Hay tres estados en el DFA reducido. El DFA reducido es el siguiente:
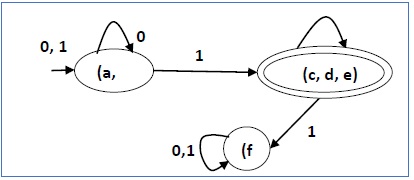
| Q | δ (q, 0) | δ (q, 1) |
|---|---|---|
| (a, b) | (a, b) | (c, d, e) |
| (c, d, e) | (c, d, e) | (F) |
| (F) | (F) | (F) |