Aritmética hexadecimal
Sistema numérico hexadecimal
A continuación se presentan las características de un sistema numérico hexadecimal.
Utiliza 10 dígitos y 6 letras, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.
Las letras representan números que comienzan en 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
También se llama sistema numérico de base 16.
Cada posición en un número hexadecimal representa una potencia 0 de la base (16). Ejemplo: 16 0
La última posición en un número hexadecimal representa una potencia x de la base (16). Ejemplo: 16 x donde x representa la última posición: 1.
Ejemplo
Número hexadecimal - 19FDE 16
Calcular el equivalente decimal -
| Paso | Número hexadecimal | Número decimal |
|---|---|---|
| Paso 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| Paso 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| Paso 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| Paso 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 normalmente se escribe como 19FDE.
Suma hexadecimal
La siguiente tabla de sumas hexadecimales le ayudará enormemente a manejar la suma hexadecimal.
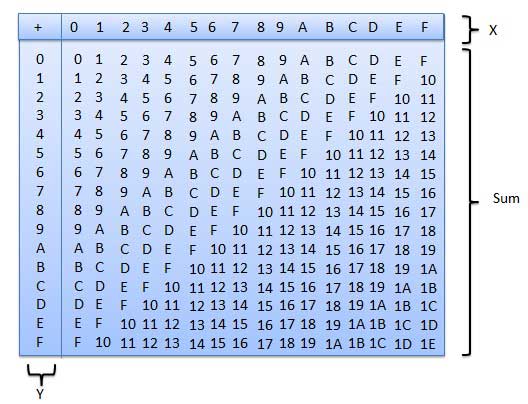
Para usar esta tabla, simplemente siga las instrucciones utilizadas en este ejemplo: agregue A 16 y 5 16 . Ubique A en la columna X y luego ubique el 5 en la columna Y. El punto en el área de 'suma' donde estas dos columnas se cruzan es la suma de dos números.
A16 + 516 = F16.Ejemplo: suma
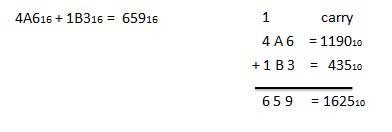
Resta hexadecimal
La resta de números hexadecimales sigue las mismas reglas que la resta de números en cualquier otro sistema numérico. La única variación está en el número prestado. En el sistema decimal, toma prestado un grupo de 10 10 . En el sistema binario, toma prestado un grupo de 2 10 . En el sistema hexadecimal, se toma prestado un grupo de 16 10 .
Ejemplo: resta
