Sincronización de hilos

La sincronización de subprocesos puede definirse como un método con la ayuda del cual podemos estar seguros de que dos o más subprocesos simultáneos no acceden simultáneamente al segmento de programa conocido como sección crítica. Por otro lado, como sabemos esa sección crítica es la parte del programa donde se accede al recurso compartido. Por lo tanto, podemos decir que la sincronización es el proceso de asegurarse de que dos o más subprocesos no interactúen entre sí al acceder a los recursos al mismo tiempo. El siguiente diagrama muestra que cuatro subprocesos intentan acceder a la sección crítica de un programa al mismo tiempo.

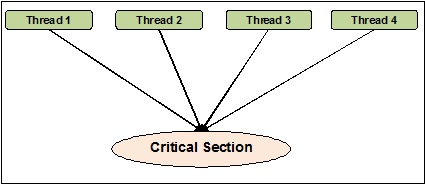
Para hacerlo más claro, suponga que dos o más subprocesos intentan agregar el objeto en la lista al mismo tiempo. Este acto no puede conducir a un final exitoso porque eliminará uno o todos los objetos o corromperá completamente el estado de la lista. Aquí, el papel de la sincronización es que solo un hilo a la vez puede acceder a la lista.

Problemas en la sincronización de subprocesos

Podríamos encontrar problemas al implementar programación concurrente o aplicar primitivas de sincronización. En esta sección, discutiremos dos temas principales. Los problemas son:

Deadlock
Condición de carrera

Condición de carrera

Este es uno de los principales problemas de la programación concurrente. El acceso simultáneo a los recursos compartidos puede provocar una condición de carrera. Una condición de carrera puede definirse como la ocurrencia de una condición cuando dos o más subprocesos pueden acceder a datos compartidos y luego intentar cambiar su valor al mismo tiempo. Debido a esto, los valores de las variables pueden ser impredecibles y variar según los tiempos de los cambios de contexto de los procesos.

Ejemplo

Considere este ejemplo para comprender el concepto de condición de carrera:

Step 1 - En este paso, necesitamos importar el módulo de subprocesos -

import threading

Step 2 - Ahora, defina una variable global, digamos x, junto con su valor como 0 -

x = 0

Step 3 - Ahora, necesitamos definir el increment_global() función, que hará el incremento en 1 en esta función global x -

def increment_global():

   global x
   x += 1

Step 4 - En este paso, definiremos el taskofThread()función, que llamará a la función increment_global () durante un número específico de veces; para nuestro ejemplo es 50000 veces -

def taskofThread():

   for _ in range(50000):
      increment_global()

Step 5- Ahora, defina la función main () en la que se crean los subprocesos t1 y t2. Ambos se iniciarán con la ayuda de la función start () y esperarán hasta que terminen sus trabajos con la ayuda de la función join ().

def main():
   global x
   x = 0
   
   t1 = threading.Thread(target= taskofThread)
   t2 = threading.Thread(target= taskofThread)

   t1.start()
   t2.start()

   t1.join()
   t2.join()

Step 6- Ahora, tenemos que dar el rango de cuántas iteraciones queremos llamar a la función main (). Aquí, lo llamamos 5 veces.

if __name__ == "__main__":
   for i in range(5):
      main()
      print("x = {1} after Iteration {0}".format(i,x))

En el resultado que se muestra a continuación, podemos ver el efecto de la condición de carrera como el valor de x después de cada iteración se espera que sea 100000. Sin embargo, hay mucha variación en el valor. Esto se debe al acceso concurrente de subprocesos a la variable global compartida x.

Salida

x = 100000 after Iteration 0
x = 54034 after Iteration 1
x = 80230 after Iteration 2
x = 93602 after Iteration 3
x = 93289 after Iteration 4

Lidiando con la condición de carrera usando bloqueos

Como hemos visto el efecto de la condición de carrera en el programa anterior, necesitamos una herramienta de sincronización que pueda manejar la condición de carrera entre múltiples subprocesos. En Python, el<threading>El módulo proporciona la clase Lock para hacer frente a la condición de carrera. Además, elLockLa clase proporciona diferentes métodos con la ayuda de los cuales podemos manejar la condición de carrera entre múltiples subprocesos. Los métodos se describen a continuación:

adquirir () método

Este método se utiliza para adquirir, es decir, bloquear un candado. Un bloqueo puede ser bloqueante o no bloqueante dependiendo del siguiente valor verdadero o falso:

With value set to True - Si se invoca el método manage () con True, que es el argumento predeterminado, la ejecución del hilo se bloquea hasta que se desbloquea.
With value set to False - Si se invoca el método generate () con False, que no es el argumento predeterminado, la ejecución del hilo no se bloquea hasta que se establece en true, es decir, hasta que se bloquea.

método release ()

Este método se utiliza para liberar un candado. A continuación se presentan algunas tareas importantes relacionadas con este método:

Si un candado está bloqueado, entonces el release()el método lo desbloquearía. Su trabajo es permitir que continúe exactamente un hilo si hay más de un hilo bloqueado y esperando que el bloqueo se desbloquee.
Levantará un ThreadError si el bloqueo ya está desbloqueado.

Ahora, podemos reescribir el programa anterior con la clase de bloqueo y sus métodos para evitar la condición de carrera. Necesitamos definir el método taskofThread () con el argumento de bloqueo y luego necesitamos usar los métodos de adquisición () y liberación () para bloquear y no bloquear bloqueos para evitar la condición de carrera.

Ejemplo

A continuación se muestra un ejemplo del programa Python para comprender el concepto de bloqueos para lidiar con la condición de carrera:

import threading

x = 0

def increment_global():

   global x
   x += 1

def taskofThread(lock):

   for _ in range(50000):
      lock.acquire()
      increment_global()
      lock.release()

def main():
   global x
   x = 0

   lock = threading.Lock()
   t1 = threading.Thread(target = taskofThread, args = (lock,))
   t2 = threading.Thread(target = taskofThread, args = (lock,))

   t1.start()
   t2.start()

   t1.join()
   t2.join()

if __name__ == "__main__":
   for i in range(5):
      main()
      print("x = {1} after Iteration {0}".format(i,x))

El siguiente resultado muestra que se ignora el efecto de la condición de carrera; ya que el valor de x, después de cada y cada iteración, es ahora 100000, lo que corresponde a las expectativas de este programa.

Salida

x = 100000 after Iteration 0
x = 100000 after Iteration 1
x = 100000 after Iteration 2
x = 100000 after Iteration 3
x = 100000 after Iteration 4

Deadlocks: el problema de los filósofos gastronómicos

El interbloqueo es un problema problemático que uno puede enfrentar al diseñar los sistemas concurrentes. Podemos ilustrar este problema con la ayuda del problema del filósofo comedor de la siguiente manera:

Edsger Dijkstra introdujo originalmente el problema del filósofo comedor, una de las ilustraciones famosas de uno de los mayores problemas del sistema concurrente llamado punto muerto.

En este problema, hay cinco filósofos famosos sentados en una mesa redonda comiendo algo de sus cuencos. Hay cinco tenedores que pueden usar los cinco filósofos para comer su comida. Sin embargo, los filósofos deciden utilizar dos tenedores al mismo tiempo para comer su comida.

Ahora bien, hay dos condiciones principales para los filósofos. Primero, cada uno de los filósofos puede estar comiendo o pensando y segundo, primero deben obtener ambas horquillas, es decir, izquierda y derecha. El problema surge cuando cada uno de los cinco filósofos logra elegir la bifurcación izquierda al mismo tiempo. Ahora todos están esperando a que el tenedor correcto esté libre, pero nunca abandonarán su tenedor hasta que hayan comido su comida y el tenedor correcto nunca esté disponible. Por lo tanto, habría un estado de punto muerto en la mesa de la cena.

Interbloqueo en sistema concurrente

Ahora, si vemos, el mismo problema también puede surgir en nuestros sistemas concurrentes. Las bifurcaciones en el ejemplo anterior serían los recursos del sistema y cada filósofo puede representar el proceso, que compite por obtener los recursos.

Solución con el programa Python

La solución de este problema se puede encontrar dividiendo a los filósofos en dos tipos: greedy philosophers y generous philosophers. Principalmente, un filósofo codicioso tratará de tomar la bifurcación izquierda y esperará hasta que esté allí. Luego esperará a que el tenedor correcto esté allí, lo recogerá, lo comerá y luego lo dejará. Por otro lado, un filósofo generoso intentará coger la bifurcación de la izquierda y si no está ahí, esperará y volverá a intentarlo pasado un tiempo. Si obtienen la bifurcación izquierda, intentarán obtener la correcta. Si también obtienen el tenedor correcto, comerán y soltarán ambos tenedores. Sin embargo, si no consiguen la bifurcación derecha, soltarán la bifurcación izquierda.

Ejemplo

El siguiente programa de Python nos ayudará a encontrar una solución al problema del filósofo gastronómico:

import threading
import random
import time

class DiningPhilosopher(threading.Thread):

   running = True

   def __init__(self, xname, Leftfork, Rightfork):
   threading.Thread.__init__(self)
   self.name = xname
   self.Leftfork = Leftfork
   self.Rightfork = Rightfork

   def run(self):
   while(self.running):
      time.sleep( random.uniform(3,13))
      print ('%s is hungry.' % self.name)
      self.dine()

   def dine(self):
   fork1, fork2 = self.Leftfork, self.Rightfork

   while self.running:
      fork1.acquire(True)
      locked = fork2.acquire(False)
	  if locked: break
      fork1.release()
      print ('%s swaps forks' % self.name)
      fork1, fork2 = fork2, fork1
   else:
      return

   self.dining()
   fork2.release()
   fork1.release()

   def dining(self):
   print ('%s starts eating '% self.name)
   time.sleep(random.uniform(1,10))
   print ('%s finishes eating and now thinking.' % self.name)

def Dining_Philosophers():
   forks = [threading.Lock() for n in range(5)]
   philosopherNames = ('1st','2nd','3rd','4th', '5th')

   philosophers= [DiningPhilosopher(philosopherNames[i], forks[i%5], forks[(i+1)%5]) \
      for i in range(5)]

   random.seed()
   DiningPhilosopher.running = True
   for p in philosophers: p.start()
   time.sleep(30)
   DiningPhilosopher.running = False
   print (" It is finishing.")

Dining_Philosophers()

El programa anterior utiliza el concepto de filósofos codiciosos y generosos. El programa también ha utilizadoacquire() y release() métodos del Lock clase de la <threading>módulo. Podemos ver la solución en el siguiente resultado:

Salida

4th is hungry.
4th starts eating
1st is hungry.
1st starts eating
2nd is hungry.
5th is hungry.
3rd is hungry.
1st finishes eating and now thinking.3rd swaps forks
2nd starts eating
4th finishes eating and now thinking.
3rd swaps forks5th starts eating
5th finishes eating and now thinking.
4th is hungry.
4th starts eating
2nd finishes eating and now thinking.
3rd swaps forks
1st is hungry.
1st starts eating
4th finishes eating and now thinking.
3rd starts eating
5th is hungry.
5th swaps forks
1st finishes eating and now thinking.
5th starts eating
2nd is hungry.
2nd swaps forks
4th is hungry.
5th finishes eating and now thinking.
3rd finishes eating and now thinking.
2nd starts eating 4th starts eating
It is finishing.