Estructuras de datos: análisis asintótico

El análisis asintótico de un algoritmo se refiere a la definición de la base / estructura matemática de su desempeño en tiempo de ejecución. Usando el análisis asintótico, podemos concluir muy bien el mejor de los casos, el caso promedio y el peor de los casos de un algoritmo.

El análisis asintótico está ligado a la entrada, es decir, si no hay entrada para el algoritmo, se concluye que funciona en un tiempo constante. Aparte de la "entrada", todos los demás factores se consideran constantes.

El análisis asintótico se refiere a calcular el tiempo de ejecución de cualquier operación en unidades matemáticas de cálculo. Por ejemplo, el tiempo de ejecución de una operación se calcula como f (n) y puede serlo para otra operación como g (n ² ). Esto significa que el tiempo de ejecución de la primera operación aumentará linealmente con el aumento den y el tiempo de ejecución de la segunda operación aumentará exponencialmente cuando naumenta. Del mismo modo, el tiempo de ejecución de ambas operaciones será casi el mismo sin es significativamente pequeño.

Por lo general, el tiempo requerido por un algoritmo se divide en tres tipos:

Best Case - Tiempo mínimo requerido para la ejecución del programa.
Average Case - Tiempo promedio requerido para la ejecución del programa.
Worst Case - Tiempo máximo requerido para la ejecución del programa.

Notaciones asintóticas

A continuación se muestran las notaciones asintóticas de uso común para calcular la complejidad del tiempo de ejecución de un algoritmo.

Ο Notación
Notación Ω
θ Notación

Notación de Big Oh, Ο

La notación Ο (n) es la forma formal de expresar el límite superior del tiempo de ejecución de un algoritmo. Mide la complejidad del tiempo en el peor de los casos o la mayor cantidad de tiempo que un algoritmo puede tardar en completarse.

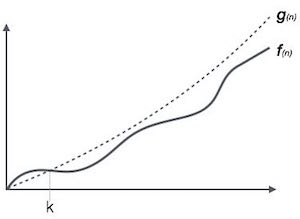
Por ejemplo, para una función f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n₀ such that f(n) ≤ c.g(n) for all n > n₀. }

Notación Omega, Ω

La notación Ω (n) es la forma formal de expresar el límite inferior del tiempo de ejecución de un algoritmo. Mide la mejor complejidad del tiempo del caso o la mejor cantidad de tiempo que un algoritmo puede tardar en completarse.

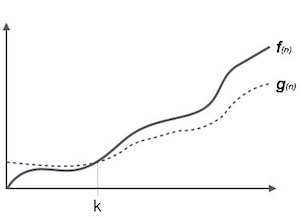
Por ejemplo, para una función f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n₀ such that g(n) ≤ c.f(n) for all n > n₀. }

Notación theta, θ

La notación θ (n) es la forma formal de expresar tanto el límite inferior como el límite superior del tiempo de ejecución de un algoritmo. Se representa de la siguiente manera:

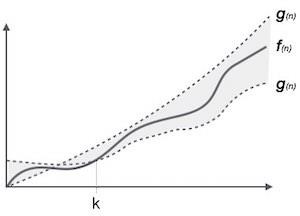
θ(f(n)) = { g(n) if and only if g(n) =  Ο(f(n)) and g(n) = Ω(f(n)) for all n > n₀. }

Notaciones asintóticas comunes

A continuación se muestra una lista de algunas notaciones asintóticas comunes:

constante	-	Ο (1)
logarítmico	-	Ο (log n)
lineal	-	Ο (n)
n log n	-	Ο (n log n)
cuadrático	-	Ο (n ² )
cúbico	-	Ο (n ³ )
polinomio	-	n ^{Ο (1)}
exponencial	-	2 ^{Ο (n)}