Estructura de datos y algoritmos: árboles AVL

¿Qué sucede si la entrada al árbol de búsqueda binaria viene ordenada (ascendente o descendente)? Entonces se verá así:

Se observa que el rendimiento en el peor de los casos de BST se acerca más a los algoritmos de búsqueda lineal, es decir, Ο (n). En datos en tiempo real, no podemos predecir el patrón de datos y sus frecuencias. Por lo tanto, surge la necesidad de equilibrar el BST existente.

El nombre de su inventor Adelson, Velski Y Landis, AVL treesson árbol de búsqueda binaria de equilibrio de altura. El árbol AVL verifica la altura de los subárboles izquierdo y derecho y asegura que la diferencia no sea mayor a 1. Esta diferencia se llamaBalance Factor.

Aquí vemos que el primer árbol está equilibrado y los siguientes dos árboles no están equilibrados.

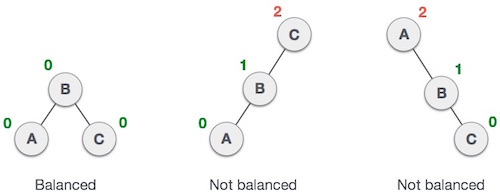
En el segundo árbol, el subárbol izquierdo de C tiene una altura 2 y el subárbol derecho tiene una altura 0, por lo que la diferencia es 2. En el tercer árbol, el subárbol derecho de Atiene altura 2 y falta la izquierda, entonces es 0, y la diferencia es 2 nuevamente. El árbol AVL permite que la diferencia (factor de equilibrio) sea solo 1.

BalanceFactor = height(left-sutree) − height(right-sutree)

Si la diferencia en la altura de los subárboles izquierdo y derecho es más de 1, el árbol se equilibra utilizando algunas técnicas de rotación.

Rotaciones AVL

Para equilibrarse, un árbol AVL puede realizar los siguientes cuatro tipos de rotaciones:

• Rotación a la izquierda
• Rotación derecha
• Rotación de izquierda a derecha
• Rotación derecha-izquierda

Las dos primeras rotaciones son rotaciones simples y las dos siguientes rotaciones son rotaciones dobles. Para tener un árbol desequilibrado, al menos necesitamos un árbol de altura 2. Con este árbol simple, vamos a entenderlos uno por uno.

Rotación izquierda

Si un árbol se desequilibra, cuando se inserta un nodo en el subárbol derecho del subárbol derecho, realizamos una única rotación a la izquierda:

En nuestro ejemplo, nodo Ase ha desequilibrado cuando se inserta un nodo en el subárbol derecho del subárbol derecho de A. Realizamos la rotación a la izquierda haciendoA el subárbol izquierdo de B.

Rotación derecha

El árbol AVL puede desequilibrarse si se inserta un nodo en el subárbol izquierdo del subárbol izquierdo. Entonces, el árbol necesita una rotación correcta.

Como se muestra, el nodo desequilibrado se convierte en el hijo derecho de su hijo izquierdo al realizar una rotación a la derecha.

Rotación de izquierda a derecha

Las rotaciones dobles son una versión ligeramente compleja de las versiones de rotaciones ya explicadas. Para comprenderlos mejor, debemos tomar nota de cada acción realizada durante la rotación. Primero veamos cómo realizar la rotación izquierda-derecha. Una rotación izquierda-derecha es una combinación de rotación izquierda seguida de rotación derecha.

Estado	Acción
	Se ha insertado un nodo en el subárbol derecho del subárbol izquierdo. Esto haceCun nodo desequilibrado. Estos escenarios hacen que el árbol AVL realice una rotación de izquierda a derecha.
	Primero realizamos la rotación izquierda en el subárbol izquierdo de C. Esto haceA, el subárbol izquierdo de B.
	Nodo C todavía está desequilibrado, sin embargo ahora, se debe al subárbol izquierdo del subárbol izquierdo.
	Ahora rotaremos a la derecha el árbol, haciendo B el nuevo nodo raíz de este subárbol. C ahora se convierte en el subárbol derecho de su propio subárbol izquierdo.
	El árbol ahora está equilibrado.

Rotación derecha-izquierda

El segundo tipo de doble rotación es la rotación derecha-izquierda. Es una combinación de rotación a la derecha seguida de rotación a la izquierda.

Estado	Acción
	Se ha insertado un nodo en el subárbol izquierdo del subárbol derecho. Esto haceA, un nodo desequilibrado con factor de equilibrio 2.
	Primero, realizamos la rotación correcta a lo largo C nodo, haciendo C el subárbol derecho de su propio subárbol izquierdo B. Ahora,B se convierte en el subárbol derecho de A.
	Nodo A todavía está desequilibrado debido al subárbol derecho de su subárbol derecho y requiere una rotación a la izquierda.
	Se realiza una rotación a la izquierda haciendo B el nuevo nodo raíz del subárbol. A se convierte en el subárbol izquierdo de su subárbol derecho B.
	El árbol ahora está equilibrado.