Matemáticas discretas - Guía rápida
Las matemáticas se pueden clasificar ampliamente en dos categorías:
Continuous Mathematics- Se basa en una recta numérica continua o en los números reales. Se caracteriza por el hecho de que entre dos números, casi siempre hay un conjunto infinito de números. Por ejemplo, una función en matemáticas continuas se puede trazar en una curva suave sin interrupciones.
Discrete Mathematics- Implica valores distintos; es decir, entre dos puntos cualesquiera, hay un número contable de puntos. Por ejemplo, si tenemos un conjunto finito de objetos, la función se puede definir como una lista de pares ordenados que tienen estos objetos y se puede presentar como una lista completa de esos pares.
Temas en matemáticas discretas
Aunque no puede haber un número definido de ramas de Matemáticas Discretas, los siguientes temas casi siempre se tratan en cualquier estudio sobre este tema:
- Conjuntos, relaciones y funciones
- Lógica matemática
- Teoría de grupos
- Teoría del conteo
- Probability
- Relaciones de inducción y recurrencia matemáticas
- Teoría de grafos
- Trees
- Álgebra de Boole
Discutiremos cada uno de estos conceptos en los capítulos siguientes de este tutorial.
Matemático alemán G. Cantorintrodujo el concepto de conjuntos. Había definido un conjunto como una colección de objetos definidos y distinguibles seleccionados por medio de ciertas reglas o descripción.
SetLa teoría forma la base de varios otros campos de estudio como la teoría del conteo, las relaciones, la teoría de grafos y las máquinas de estados finitos. En este capítulo, cubriremos los diferentes aspectos deSet Theory.
Conjunto - Definición
Un conjunto es una colección desordenada de diferentes elementos. Un conjunto se puede escribir explícitamente enumerando sus elementos utilizando corchetes de conjuntos. Si se cambia el orden de los elementos o se repite cualquier elemento de un conjunto, no realiza ningún cambio en el conjunto.
Algunos ejemplos de conjuntos
- Un conjunto de todos los enteros positivos
- Un conjunto de todos los planetas del sistema solar.
- Un conjunto de todos los estados de la India.
- Un conjunto de todas las letras minúsculas del alfabeto.
Representación de un conjunto
Los conjuntos se pueden representar de dos formas:
- Formulario de lista o tabular
- Establecer notación de constructor
Formulario de lista o tabular
El conjunto se representa enumerando todos los elementos que lo componen. Los elementos están encerrados entre llaves y separados por comas.
Example 1 - Conjunto de vocales en alfabeto inglés, $A = \lbrace a,e,i,o,u \rbrace$
Example 2 - Conjunto de números impares menores a 10, $B = \lbrace 1,3,5,7,9 \rbrace$
Establecer notación de constructor
El conjunto se define especificando una propiedad que los elementos del conjunto tienen en común. El conjunto se describe como$A = \lbrace x : p(x) \rbrace$
Example 1 - El conjunto $\lbrace a,e,i,o,u \rbrace$ está escrito como -
$A = \lbrace x : \text{x is a vowel in English alphabet} \rbrace$
Example 2 - El conjunto $\lbrace 1,3,5,7,9 \rbrace$ está escrito como -
$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$
Si un elemento x es miembro de cualquier conjunto S, se denota por $x \in S$ y si un elemento y no es miembro del conjunto S, se denota por $y \notin S$.
Example- si$S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ pero $1.5 \notin S$
Algunos conjuntos importantes
N - el conjunto de todos los números naturales = $\lbrace1, 2, 3, 4, .....\rbrace$
Z - el conjunto de todos los enteros = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$
Z+ - el conjunto de todos los enteros positivos
Q - el conjunto de todos los números racionales
R - el conjunto de todos los números reales
W - el conjunto de todos los números enteros
Cardinalidad de un conjunto
Cardinalidad de un conjunto S, denotado por $|S|$, es el número de elementos del conjunto. El número también se conoce como número cardinal. Si un conjunto tiene un número infinito de elementos, su cardinalidad es$\infty$.
Example - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$
Si hay dos conjuntos X e Y,
$|X| = |Y|$denota dos conjuntos X e Y que tienen la misma cardinalidad. Ocurre cuando el número de elementos en X es exactamente igual al número de elementos en Y. En este caso, existe una función biyectiva 'f' de X a Y.
$|X| \le |Y|$denota que la cardinalidad del conjunto X es menor o igual que la cardinalidad del conjunto Y. Ocurre cuando el número de elementos en X es menor o igual al de Y. Aquí, existe una función inyectiva 'f' de X a Y.
$|X| \lt |Y|$denota que la cardinalidad del conjunto X es menor que la cardinalidad del conjunto Y. Ocurre cuando el número de elementos en X es menor que el de Y. Aquí, la función 'f' de X a Y es una función inyectiva pero no biyectiva.
$If\ |X| \le |Y|$ y $|X| \ge |Y|$ luego $|X| = |Y|$. Los conjuntos X e Y se denominan comúnmente conjuntos equivalentes.
Tipos de conjuntos
Los conjuntos se pueden clasificar en muchos tipos. Algunos de los cuales son finitos, infinitos, subconjuntos, universales, propios, conjuntos únicos, etc.
Conjunto finito
Un conjunto que contiene un número definido de elementos se denomina conjunto finito.
Example - $S = \lbrace x \:| \:x \in N$ y $70 \gt x \gt 50 \rbrace$
Conjunto infinito
Un conjunto que contiene un número infinito de elementos se llama conjunto infinito.
Example - $S = \lbrace x \: | \: x \in N $ y $ x \gt 10 \rbrace$
Subconjunto
Un conjunto X es un subconjunto del conjunto Y (escrito como $X \subseteq Y$) si cada elemento de X es un elemento del conjunto Y.
Example 1 - Deja, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ y $Y = \lbrace 1, 2 \rbrace$. Aquí el conjunto Y es un subconjunto del conjunto X ya que todos los elementos del conjunto Y están en el conjunto X. Por lo tanto, podemos escribir$Y \subseteq X$.
Example 2 - Deja, $X = \lbrace 1, 2, 3 \rbrace$ y $Y = \lbrace 1, 2, 3 \rbrace$. Aquí el conjunto Y es un subconjunto (no un subconjunto propio) del conjunto X ya que todos los elementos del conjunto Y están en el conjunto X. Por lo tanto, podemos escribir$Y \subseteq X$.
Subconjunto propio
El término "subconjunto adecuado" puede definirse como "subconjunto de pero no igual a". Un conjunto X es un subconjunto propio del conjunto Y (escrito como$ X \subset Y $) si cada elemento de X es un elemento del conjunto Y y $|X| \lt |Y|$.
Example - Deja, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ y $Y = \lbrace 1, 2 \rbrace$. Aquí establece$Y \subset X$ ya que todos los elementos en $Y$ están contenidos en $X$ también y $X$ tiene al menos un elemento está más que establecido $Y$.
Conjunto universal
Es una colección de todos los elementos en un contexto o aplicación particular. Todos los conjuntos en ese contexto o aplicación son esencialmente subconjuntos de este conjunto universal. Los conjuntos universales se representan como$U$.
Example - Podemos definir $U$como el conjunto de todos los animales de la tierra. En este caso, el conjunto de todos los mamíferos es un subconjunto de$U$, el conjunto de todos los peces es un subconjunto de $U$, el conjunto de todos los insectos es un subconjunto de $U$, y así.
Conjunto vacío o conjunto nulo
Un conjunto vacío no contiene elementos. Se denota por$\emptyset$. Como el número de elementos de un conjunto vacío es finito, el conjunto vacío es un conjunto finito. La cardinalidad del conjunto vacío o del conjunto nulo es cero.
Example - $S = \lbrace x \:| \: x \in N$ y $7 \lt x \lt 8 \rbrace = \emptyset$
Conjunto Singleton o Conjunto de unidades
El conjunto singleton o conjunto de unidades contiene solo un elemento. Un conjunto singleton se denota por$\lbrace s \rbrace$.
Example - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$
Conjunto igual
Si dos conjuntos contienen los mismos elementos, se dice que son iguales.
Example - si $A = \lbrace 1, 2, 6 \rbrace$ y $B = \lbrace 6, 1, 2 \rbrace$, son iguales ya que cada elemento del conjunto A es un elemento del conjunto B y cada elemento del conjunto B es un elemento del conjunto A.
Conjunto equivalente
Si las cardinalidades de dos conjuntos son iguales, se denominan conjuntos equivalentes.
Example - si $A = \lbrace 1, 2, 6 \rbrace$ y $B = \lbrace 16, 17, 22 \rbrace$, son equivalentes ya que la cardinalidad de A es igual a la cardinalidad de B. ie $|A| = |B| = 3$
Conjunto superpuesto
Dos conjuntos que tienen al menos un elemento común se denominan conjuntos superpuestos.
En caso de conjuntos superpuestos:
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
$n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$
$n(A) = n(A - B) + n(A \cap B)$
$n(B) = n(B - A) + n(A \cap B)$
Example - Deja, $A = \lbrace 1, 2, 6 \rbrace$ y $B = \lbrace 6, 12, 42 \rbrace$. Hay un elemento común '6', por lo que estos conjuntos son conjuntos superpuestos.
Conjunto disjunto
Dos conjuntos A y B se denominan conjuntos disjuntos si no tienen ni siquiera un elemento en común. Por lo tanto, los conjuntos disjuntos tienen las siguientes propiedades:
$n(A \cap B) = \emptyset$
$n(A \cup B) = n(A) + n(B)$
Example - Deja, $A = \lbrace 1, 2, 6 \rbrace$ y $B = \lbrace 7, 9, 14 \rbrace$, no hay un solo elemento común, por lo tanto, estos conjuntos son conjuntos superpuestos.
Diagramas de Venn
El diagrama de Venn, inventado en 1880 por John Venn, es un diagrama esquemático que muestra todas las posibles relaciones lógicas entre diferentes conjuntos matemáticos.
Examples
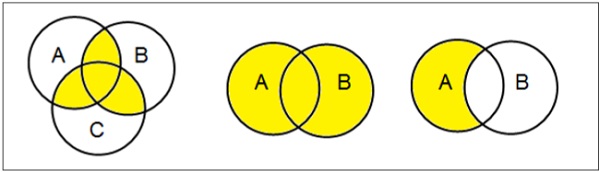
Establecer operaciones
Las operaciones de conjuntos incluyen Unión de conjuntos, Intersección de conjuntos, Diferencia de conjuntos, Complemento de conjunto y Producto cartesiano.
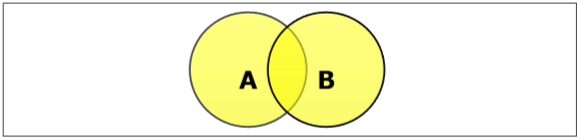
Establecer unión
La unión de los conjuntos A y B (denotada por $A \cup B$) es el conjunto de elementos que están en A, en B, o tanto en A como en B. $A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$.
Example - si $A = \lbrace 10, 11, 12, 13 \rbrace$ y B = $\lbrace 13, 14, 15 \rbrace$, luego $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$. (El elemento común ocurre solo una vez)
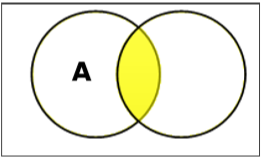
Establecer intersección
La intersección de los conjuntos A y B (denotada por $A \cap B$) es el conjunto de elementos que están tanto en A como en B. Por lo tanto, $A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$.
Example - si $A = \lbrace 11, 12, 13 \rbrace$ y $B = \lbrace 13, 14, 15 \rbrace$, luego $A \cap B = \lbrace 13 \rbrace$.
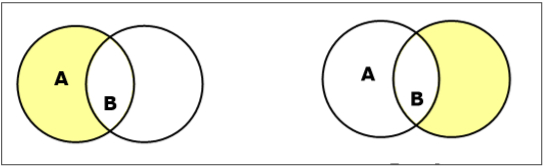
Establecer diferencia / complemento relativo
La diferencia de conjuntos de los conjuntos A y B (denotada por $A – B$) es el conjunto de elementos que están solo en A pero no en B. Por lo tanto, $A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$.
Example - si $A = \lbrace 10, 11, 12, 13 \rbrace$ y $B = \lbrace 13, 14, 15 \rbrace$, luego $(A - B) = \lbrace 10, 11, 12 \rbrace$ y $(B - A) = \lbrace 14, 15 \rbrace$. Aquí podemos ver$(A - B) \ne (B - A)$
Complemento de un conjunto
El complemento de un conjunto A (denotado por $A’$) es el conjunto de elementos que no están en el conjunto A. Por lo tanto, $A' = \lbrace x | x \notin A \rbrace$.
Más específicamente, $A'= (U - A)$ dónde $U$ es un conjunto universal que contiene todos los objetos.
Example - si $A = \lbrace x \:| \: x\ \: {belongs\: to\: set\: of\: odd \:integers} \rbrace$ luego $A' = \lbrace y\: | \: y\ \: {does\: not\: belong\: to\: set\: of\: odd\: integers } \rbrace$
Producto cartesiano / producto cruzado
El producto cartesiano de n número de conjuntos $A_1, A_2, \dots A_n$ denotado como $A_1 \times A_2 \dots \times A_n$ se puede definir como todos los pares ordenados posibles $(x_1, x_2, \dots x_n)$ dónde $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$
Example - Si tomamos dos juegos $A = \lbrace a, b \rbrace$ y $B = \lbrace 1, 2 \rbrace$,
El producto cartesiano de A y B se escribe como: $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$
El producto cartesiano de B y A se escribe como: $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$
Set de poder
El conjunto de potencia de un conjunto S es el conjunto de todos los subconjuntos de S, incluido el conjunto vacío. La cardinalidad de un conjunto de potencias de un conjunto S de cardinalidad n es$2^n$. El conjunto de potencia se denota como$P(S)$.
Example −
Para un juego $S = \lbrace a, b, c, d \rbrace$ calculemos los subconjuntos -
Subconjuntos con 0 elementos - $\lbrace \emptyset \rbrace$ (el juego vacío)
Subconjuntos con 1 elemento - $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$
Subconjuntos con 2 elementos - $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$
Subconjuntos con 3 elementos - $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$
Subconjuntos con 4 elementos - $\lbrace a, b, c, d \rbrace$
Por lo tanto, $P(S)=$
$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$
$| P(S) | = 2^4 = 16$
Note - El conjunto de potencia de un conjunto vacío también es un conjunto vacío.
$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$
Partición de un conjunto
La partición de un conjunto, digamos S , es una colección de n subconjuntos disjuntos, digamos$P_1, P_2, \dots P_n$ que cumpla las siguientes tres condiciones:
$P_i$ no contiene el conjunto vacío.
$\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$
La unión de los subconjuntos debe ser igual a todo el conjunto original.
$\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$
La intersección de dos conjuntos distintos está vacía.
$\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ where\ n \ge a,\: b \ge 0 \rbrack$
Example
Dejar $S = \lbrace a, b, c, d, e, f, g, h \rbrace$
Una partición probable es $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$
Otra probable partición es $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$
Números de campana
Los números de campana dan el recuento de la cantidad de formas de particionar un conjunto. Están denotados por$B_n$ donde n es la cardinalidad del conjunto.
Example -
Dejar $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$
Las particiones alternativas son:
1. $\emptyset , \lbrace 1, 2, 3 \rbrace$
2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$
3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$
4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$
5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$
Por lo tanto $B_3 = 5$
Siempre que se discuten los conjuntos, la relación entre los elementos de los conjuntos es lo siguiente que surge. Relations puede existir entre objetos del mismo conjunto o entre objetos de dos o más conjuntos.
Definición y propiedades
Una relación binaria R del conjunto xay (escrito como $xRy$ o $R(x,y)$) es un subconjunto del producto cartesiano $x \times y$. Si el par ordenado de G se invierte, la relación también cambia.
Generalmente una relación n-aria R entre conjuntos $A_1, \dots ,\ and\ A_n$ es un subconjunto del producto n-ario $A_1 \times \dots \times A_n$. La cardinalidad mínima de una relación R es cero y la máxima es$n^2$ en este caso.
Una relación binaria R en un solo conjunto A es un subconjunto de $A \times A$.
Para dos conjuntos distintos, A y B, que tienen cardinalidades m y n respectivamente, la cardinalidad máxima de una relación R de A a B es mn .
Dominio y rango
Si hay dos conjuntos A y B, y la relación R tiene un par de orden (x, y), entonces -
los domain de R, Dom (R), es el conjunto $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$
los range de R, Ran (R), es el conjunto $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$
Ejemplos
Dejar, $A = \lbrace 1, 2, 9 \rbrace $ y $ B = \lbrace 1, 3, 7 \rbrace$
Caso 1 - Si la relación R es 'igual a' entonces $R = \lbrace (1, 1), (3, 3) \rbrace$
Dom (R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
Caso 2 - Si la relación R es 'menor que' entonces $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
Dom (R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
Caso 3 - Si la relación R es 'mayor que' entonces $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
Dom (R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
Representación de relaciones usando Graph
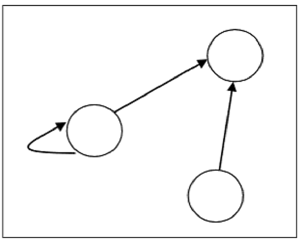
Una relación se puede representar mediante un gráfico dirigido.
El número de vértices del gráfico es igual al número de elementos del conjunto a partir del cual se ha definido la relación. Para cada par ordenado (x, y) en la relación R, habrá un borde dirigido desde el vértice 'x' al vértice 'y'. Si hay un par ordenado (x, x), habrá un bucle automático en el vértice 'x'.
Supongamos que hay una relación $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ en el set $S = \lbrace 1, 2, 3 \rbrace$, se puede representar mediante el siguiente gráfico:
Tipos de relaciones
los Empty Relation entre los conjuntos X e Y, o en E, es el conjunto vacío $\emptyset$
los Full Relation entre los conjuntos X e Y es el conjunto $X \times Y$
los Identity Relation en el set X es el set $\lbrace (x, x) | x \in X \rbrace$
La relación inversa R 'de una relación R se define como - $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
Example - si $R = \lbrace (1, 2), (2, 3) \rbrace$ luego $R' $ estarán $\lbrace (2, 1), (3, 2) \rbrace$
Una relación R en el conjunto A se llama Reflexive Si $\forall a \in A$ está relacionado con a (aRa sostiene)
Example - La relación $R = \lbrace (a, a), (b, b) \rbrace$ en el set $X = \lbrace a, b \rbrace$ es reflexivo.
Una relación R en el conjunto A se llama Irreflexive si no $a \in A$ está relacionado con a (aRa no se sostiene).
Example - La relación $R = \lbrace (a, b), (b, a) \rbrace$ en el set $X = \lbrace a, b \rbrace$ es irreflexivo.
Una relación R en el conjunto A se llama Symmetric Si $xRy$ implica $yRx$, $\forall x \in A$ y $\forall y \in A$.
Example - La relación $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ en el set $A = \lbrace 1, 2, 3 \rbrace$ es simétrico.
Una relación R en el conjunto A se llama Anti-Symmetric Si $xRy$ y $yRx$ implica $x = y \: \forall x \in A$ y $\forall y \in A$.
Example - La relación $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ es antisimétrico ya que $x \leq y$ y $y \leq x$ implica $x = y$.
Una relación R en el conjunto A se llama Transitive Si $xRy$ y $yRz$ implica $xRz, \forall x,y,z \in A$.
Example - La relación $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ en el set $A = \lbrace 1, 2, 3 \rbrace$ es transitivo.
Una relación es una Equivalence Relation si es reflexiva, simétrica y transitiva.
Example - La relación $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ en el set $A = \lbrace 1, 2, 3 \rbrace$ es una relación de equivalencia ya que es reflexiva, simétrica y transitiva.
UN Functionasigna a cada elemento de un conjunto, exactamente un elemento de un conjunto relacionado. Las funciones encuentran su aplicación en varios campos como la representación de la complejidad computacional de los algoritmos, el conteo de objetos, el estudio de secuencias y cadenas, por nombrar algunos. El tercer y último capítulo de esta parte destaca los aspectos importantes de las funciones.
Función - Definición
Una función o mapeo (definido como $f: X \rightarrow Y$) es una relación de elementos de un conjunto X a elementos de otro conjunto Y (X e Y son conjuntos no vacíos). X se llama dominio e Y se llama codominio de función 'f'.
La función 'f' es una relación en X e Y tal que para cada $x \in X$, existe un único $y \in Y$ tal que $(x,y) \in R$. 'x' se llama pre-imagen y 'y' se llama imagen de la función f.
Una función puede ser una a una o muchas a una, pero no una a muchas.
Función inyectiva / uno a uno
Una función $f: A \rightarrow B$ es una función inyectiva o uno a uno si para cada $b \in B$, existe como máximo uno $a \in A$ tal que $f(s) = t$.
Esto significa una función f es inyectable si $a_1 \ne a_2$ implica $f(a1) \ne f(a2)$.
Ejemplo
$f: N \rightarrow N, f(x) = 5x$ es inyectable.
$f: N \rightarrow N, f(x) = x^2$ es inyectable.
$f: R\rightarrow R, f(x) = x^2$ no es inyectable como $(-x)^2 = x^2$
Función sobreyectiva / sobre
Una función $f: A \rightarrow B$es sobreyectiva (sobre) si la imagen de f es igual a su rango. De manera equivalente, para cada$b \in B$, existe algo $a \in A$ tal que $f(a) = b$. Esto significa que para cualquier y en B, existe una x en A tal que$y = f(x)$.
Ejemplo
$f : N \rightarrow N, f(x) = x + 2$ es sobreyectiva.
$f : R \rightarrow R, f(x) = x^2$ no es sobreyectiva ya que no podemos encontrar un número real cuyo cuadrado sea negativo.
Corresponsal Bijective / One-to-one
Una función $f: A \rightarrow B$ es corresponsal bijetivo o uno a uno si y solo si f es tanto inyectiva como sobreyectiva.
Problema
Demuestre que una función $f: R \rightarrow R$ definido por $f(x) = 2x – 3$ es una función biyectiva.
Explanation - Tenemos que demostrar que esta función es tanto inyectiva como sobreyectiva.
Si $f(x_1) = f(x_2)$, luego $2x_1 – 3 = 2x_2 – 3 $ e implica que $x_1 = x_2$.
Por tanto, f es injective.
Aquí, $2x – 3= y$
Entonces, $x = (y+5)/3$ que pertenece a R y $f(x) = y$.
Por tanto, f es surjective.
Ya que f es ambos surjective y injective, podemos decir f es bijective.
Inversa de una función
los inverse de una función correspondiente uno a uno $f : A \rightarrow B$, es la función $g : B \rightarrow A$, con la siguiente propiedad:
$f(x) = y \Leftrightarrow g(y) = x$
La función f se llama invertible, si existe su función inversa g.
Ejemplo
Una función $f : Z \rightarrow Z, f(x)=x+5$, es invertible ya que tiene la función inversa $ g : Z \rightarrow Z, g(x)= x-5$.
Una función $f : Z \rightarrow Z, f(x)=x^2$ no es invertible ya que no es uno a uno como $(-x)^2=x^2$.
Composición de funciones
Dos funciones $f: A \rightarrow B$ y $g: B \rightarrow C$ se puede componer para dar una composición $g o f$. Esta es una función de A a C definida por$(gof)(x) = g(f(x))$
Ejemplo
Dejar $f(x) = x + 2$ y $g(x) = 2x + 1$, encontrar $( f o g)(x)$ y $( g o f)(x)$.
Solución
$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$
$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$
Por lo tanto, $(f o g)(x) \neq (g o f)(x)$
Algunos hechos sobre la composición
Si f y g son uno a uno, entonces la función $(g o f)$ también es uno a uno.
Si f y g están en, entonces la función $(g o f)$ también está en.
La composición siempre tiene propiedad asociativa pero no tiene propiedad conmutativa.
Las reglas de la lógica matemática especifican métodos de razonamiento de enunciados matemáticos. El filósofo griego Aristóteles fue el pionero del razonamiento lógico. El razonamiento lógico proporciona la base teórica para muchas áreas de las matemáticas y, en consecuencia, la informática. Tiene muchas aplicaciones prácticas en informática como diseño de máquinas informáticas, inteligencia artificial, definición de estructuras de datos para lenguajes de programación, etc.
Propositional Logicse ocupa de enunciados a los que se pueden asignar valores de verdad, "verdadero" y "falso". El propósito es analizar estas declaraciones de forma individual o compuesta.
Lógica preposicional - Definición
Una proposición es una colección de enunciados declarativos que tiene un valor de verdad "verdadero" o un valor de verdad "falso". Una proposicional consta de variables proposicionales y conectivos. Denotamos las variables proposicionales con letras mayúsculas (A, B, etc.). Los conectivos conectan las variables proposicionales.
A continuación se dan algunos ejemplos de propuestas:
- "El hombre es mortal", devuelve el valor de verdad "VERDADERO"
- "12 + 9 = 3 - 2", devuelve el valor verdadero "FALSO"
Lo siguiente no es una propuesta:
"A es menor que 2". Se debe a que, a menos que demos un valor específico de A, no podemos decir si el enunciado es verdadero o falso.
Conectivos
En lógica proposicional generalmente usamos cinco conectivos que son:
O ($\lor$)
Y ($\land$)
Negación / NO ($\lnot$)
Implicación / si-entonces ($\rightarrow$)
Si y solo si ($\Leftrightarrow$).
OR ($\lor$) - La operación OR de dos proposiciones A y B (escrito como $A \lor B$) es verdadera si al menos alguna de las variables proposicionales A o B es verdadera.
La tabla de verdad es la siguiente:
| UN | segundo | A ∨ B |
|---|---|---|
| Cierto | Cierto | Cierto |
| Cierto | Falso | Cierto |
| Falso | Cierto | Cierto |
| Falso | Falso | Falso |
AND ($\land$) - La operación AND de dos proposiciones A y B (escrito como $A \land B$) es verdadera si tanto la variable proposicional A como la B son verdaderas.
La tabla de verdad es la siguiente:
| UN | segundo | A ∧ B |
|---|---|---|
| Cierto | Cierto | Cierto |
| Cierto | Falso | Falso |
| Falso | Cierto | Falso |
| Falso | Falso | Falso |
Negation ($\lnot$) - La negación de una proposición A (escrita como $\lnot A$) es falso cuando A es verdadero y es verdadero cuando A es falso.
La tabla de verdad es la siguiente:
| UN | ¬ A |
|---|---|
| Cierto | Falso |
| Falso | Cierto |
Implication / if-then ($\rightarrow$) - Una implicación $A \rightarrow B$es la proposición "si A, entonces B". Es falso si A es verdadero y B es falso. Los demás casos son ciertos.
La tabla de verdad es la siguiente:
| UN | segundo | A → B |
|---|---|---|
| Cierto | Cierto | Cierto |
| Cierto | Falso | Falso |
| Falso | Cierto | Cierto |
| Falso | Falso | Cierto |
If and only if ($ \Leftrightarrow $) - $A \Leftrightarrow B$ es conectivo lógico bi-condicional que es verdadero cuando pyq son iguales, es decir, ambos son falsos o ambos son verdaderos.
La tabla de verdad es la siguiente:
| UN | segundo | A ⇔ B |
|---|---|---|
| Cierto | Cierto | Cierto |
| Cierto | Falso | Falso |
| Falso | Cierto | Falso |
| Falso | Falso | Cierto |
Tautologías
Una tautología es una fórmula que siempre es cierta para cada valor de sus variables proposicionales.
Example - Demuestra $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ es una tautología
La tabla de verdad es la siguiente:
| UN | segundo | A → B | (A → B) ∧ A | [(A → B) ∧ A] → B |
|---|---|---|---|---|
| Cierto | Cierto | Cierto | Cierto | Cierto |
| Cierto | Falso | Falso | Falso | Cierto |
| Falso | Cierto | Cierto | Falso | Cierto |
| Falso | Falso | Cierto | Falso | Cierto |
Como podemos ver cada valor de $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ es "Verdadero", es una tautología.
Contradicciones
Una contradicción es una fórmula que siempre es falsa para cada valor de sus variables proposicionales.
Example - Demuestra $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ es una contradiccion
La tabla de verdad es la siguiente:
| UN | segundo | A ∨ B | ¬ A | ¬ B | (¬ A) ∧ (¬ B) | (A ∨ B) ∧ [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| Cierto | Cierto | Cierto | Falso | Falso | Falso | Falso |
| Cierto | Falso | Cierto | Falso | Cierto | Falso | Falso |
| Falso | Cierto | Cierto | Cierto | Falso | Falso | Falso |
| Falso | Falso | Falso | Cierto | Cierto | Cierto | Falso |
Como podemos ver cada valor de $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ es "falso", es una contradicción.
Contingencia
Una contingencia es una fórmula que tiene valores verdaderos y falsos para cada valor de sus variables proposicionales.
Example - Demuestra $(A \lor B) \land (\lnot A)$ una contingencia
La tabla de verdad es la siguiente:
| UN | segundo | A ∨ B | ¬ A | (A ∨ B) ∧ (¬ A) |
|---|---|---|---|---|
| Cierto | Cierto | Cierto | Falso | Falso |
| Cierto | Falso | Cierto | Falso | Falso |
| Falso | Cierto | Cierto | Cierto | Cierto |
| Falso | Falso | Falso | Cierto | Falso |
Como podemos ver cada valor de $(A \lor B) \land (\lnot A)$ tiene tanto "Verdadero" como "Falso", es una contingencia.
Equivalencias proposicionales
Dos declaraciones X e Y son lógicamente equivalentes si se cumple alguna de las dos condiciones siguientes:
Las tablas de verdad de cada declaración tienen los mismos valores de verdad.
La declaración bi-condicional $X \Leftrightarrow Y$ es una tautología.
Example - Demuestra $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ son equivalentes
Prueba por el primer método (tabla de verdad coincidente)
| UN | segundo | A ∨ B | ¬ (A ∨ B) | ¬ A | ¬ B | [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| Cierto | Cierto | Cierto | Falso | Falso | Falso | Falso |
| Cierto | Falso | Cierto | Falso | Falso | Cierto | Falso |
| Falso | Cierto | Cierto | Falso | Cierto | Falso | Falso |
| Falso | Falso | Falso | Cierto | Cierto | Cierto | Cierto |
Aquí, podemos ver los valores de verdad de $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ son iguales, por lo tanto, las declaraciones son equivalentes.
Probando por 2 nd método (Bi-condicionalidad)
| UN | segundo | ¬ (A ∨ B) | [(¬ A) ∧ (¬ B)] | [¬ (A ∨ B)] ⇔ [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|
| Cierto | Cierto | Falso | Falso | Cierto |
| Cierto | Falso | Falso | Falso | Cierto |
| Falso | Cierto | Falso | Falso | Cierto |
| Falso | Falso | Cierto | Cierto | Cierto |
Como $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ es una tautología, los enunciados son equivalentes.
Inversa, Conversa y Contra-positiva
Implicación / si-entonces $(\rightarrow)$también se denomina declaración condicional. Tiene dos partes:
- Hipótesis, p
- Conclusión, q
Como se mencionó anteriormente, se denota como $p \rightarrow q$.
Example of Conditional Statement- “Si haces tu tarea, no serás castigado”. Aquí, "haces tu tarea" es la hipótesis, p, y "no serás castigado" es la conclusión, q.
Inverse- Una inversa del enunciado condicional es la negación tanto de la hipótesis como de la conclusión. Si el enunciado es "Si p, entonces q", la inversa será "Si no p, entonces no q". Así, la inversa de$p \rightarrow q$ es $ \lnot p \rightarrow \lnot q$.
Example - Lo inverso de "Si haces tu tarea, no serás castigado" es "Si no haces tu tarea, serás castigado".
Converse- El inverso del enunciado condicional se calcula intercambiando la hipótesis y la conclusión. Si el enunciado es "Si p, entonces q", la inversa será "Si q, entonces p". El inverso de$p \rightarrow q$ es $q \rightarrow p$.
Example - Lo contrario de "Si haces tu tarea, no serás castigado" es "Si no serás castigado, haz tu tarea".
Contra-positive- El contra-positivo del condicional se calcula intercambiando la hipótesis y la conclusión del enunciado inverso. Si el enunciado es "Si p, entonces q", el contra-positivo será "Si no q, entonces no p". El contra-positivo de$p \rightarrow q$ es $\lnot q \rightarrow \lnot p$.
Example - El contra-positivo de "Si haces tu tarea, no serás castigado" es "Si te castigan, no hiciste tu tarea".
Principio de dualidad
El principio de dualidad establece que para cualquier enunciado verdadero, el enunciado dual obtenido al intercambiar uniones en intersecciones (y viceversa) e intercambiar un conjunto universal en un conjunto nulo (y viceversa) también es cierto. Si el doble de cualquier enunciado es el enunciado en sí mismo, se diceself-dual declaración.
Example - El dual de $(A \cap B ) \cup C$ es $(A \cup B) \cap C$
Formas normales
Podemos convertir cualquier proposición en dos formas normales:
- Forma conjuntiva normal
- Forma normal disyuntiva
Forma normal conjuntiva
Un enunciado compuesto está en forma normal conjuntiva si se obtiene operando Y entre variables (negación de variables incluidas) conectadas con OR. En términos de operaciones de conjuntos, es un enunciado compuesto obtenido por intersección entre variables conectadas con uniones.
Examples
$(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$
$(P \cup Q) \cap (Q \cup R)$
Forma normal disyuntiva
Un enunciado compuesto está en forma disyuntiva normal si se obtiene operando OR entre variables (negación de variables incluidas) conectadas con AND. En términos de operaciones de conjuntos, es un enunciado compuesto obtenido por Unión entre variables conectadas con Intersecciones.
Examples
$(A \land B) \lor (A \land C) \lor (B \land C \land D)$
$(P \cap Q) \cup (Q \cap R)$
Predicate Logic se ocupa de los predicados, que son proposiciones que contienen variables.
Lógica de predicados - Definición
Un predicado es una expresión de una o más variables definidas en algún dominio específico. Un predicado con variables puede convertirse en una proposición, ya sea asignando un valor a la variable o cuantificándola.
Los siguientes son algunos ejemplos de predicados:
- Deje que E (x, y) denote "x = y"
- Sea X (a, b, c) "a + b + c = 0"
- Sea M (x, y) "x está casada con y"
Fórmula bien formada
La fórmula bien formada (wff) es un predicado que contiene cualquiera de los siguientes:
Todas las constantes proposicionales y variables proposicionales son wffs
Si x es una variable e Y es una wff, $\forall x Y$ y $\exists x Y$ también son wff
El valor de verdad y los valores falsos son wffs
Cada fórmula atómica es un wff
Todos los conectivos que conectan wffs son wffs
Cuantificadores
La variable de predicados se cuantifica mediante cuantificadores. Hay dos tipos de cuantificadores en la lógica de predicados: el cuantificador universal y el cuantificador existencial.
Cuantificador universal
El cuantificador universal establece que las declaraciones dentro de su alcance son verdaderas para cada valor de la variable específica. Se denota con el símbolo$\forall$.
$\forall x P(x)$ se lee como para cada valor de x, P (x) es verdadero.
Example - "El hombre es mortal" se puede transformar en la forma proposicional $\forall x P(x)$ donde P (x) es el predicado que denota que x es mortal y el universo del discurso son todos los hombres.
Cuantificador existencial
El cuantificador existencial establece que las declaraciones dentro de su alcance son verdaderas para algunos valores de la variable específica. Se denota con el símbolo$\exists $.
$\exists x P(x)$ se lee como para algunos valores de x, P (x) es verdadero.
Example - "Algunas personas son deshonestas" se puede transformar en la forma proposicional $\exists x P(x)$ donde P (x) es el predicado que denota que x es deshonesto y el universo del discurso son algunas personas.
Cuantificadores anidados
Si usamos un cuantificador que aparece dentro del alcance de otro cuantificador, se llama cuantificador anidado.
Example
$\forall\ a\: \exists b\: P (x, y)$ dónde $P (a, b)$ denota $a + b = 0$
$\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ dónde $P (a, b)$ denota $a + (b + c) = (a + b) + c$
Note - $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$
Para deducir nuevos enunciados de los enunciados cuya verdad que ya conocemos, Rules of Inference son usados.
¿Para qué sirven las reglas de inferencia?
La lógica matemática se usa a menudo para pruebas lógicas. Las pruebas son argumentos válidos que determinan los valores de verdad de los enunciados matemáticos.
Un argumento es una secuencia de declaraciones. El último enunciado es la conclusión y todos sus enunciados precedentes se denominan premisas (o hipótesis). El símbolo "$\therefore$”, (Leer por tanto) se coloca antes de la conclusión. Un argumento válido es aquel en el que la conclusión se deriva de los valores de verdad de las premisas.
Las reglas de inferencia proporcionan las plantillas o pautas para construir argumentos válidos a partir de las declaraciones que ya tenemos.
Tabla de reglas de inferencia
| Regla de inferencia | Nombre | Regla de inferencia | Nombre |
|---|---|---|---|
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$ |
Adición |
$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$ |
Silogismo disyuntivo |
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$ |
Conjunción |
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$ |
Silogismo hipotético |
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$ |
Simplificación |
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$ |
Dilema constructivo |
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$ |
Modus ponens |
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$ |
Dilema destructivo |
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$ |
Modus Tollens |
Adición
Si P es una premisa, podemos usar la regla de la suma para derivar $ P \lor Q $.
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$
Ejemplo
Sea P la proposición, "Él estudia mucho" es verdad
Por lo tanto - "O estudia mucho o es un muy mal estudiante". Aquí Q es la proposición “es un muy mal estudiante”.
Conjunción
Si P y Q son dos premisas, podemos usar la regla de conjunción para derivar $ P \land Q $.
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$
Ejemplo
Deje P - "Él estudia mucho"
Deje Q: "Es el mejor chico de la clase"
Por lo tanto: "Estudia mucho y es el mejor chico de la clase".
Simplificación
Si $P \land Q$ es una premisa, podemos usar la regla de simplificación para derivar P.
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$
Ejemplo
"Estudia mucho y es el mejor chico de la clase", $P \land Q$
Por lo tanto - "Él estudia mucho"
Modus ponens
Si P y $P \rightarrow Q$ son dos premisas, podemos usar Modus Ponens para derivar Q.
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$
Ejemplo
"If you have a password, then you can log on to facebook", $P \rightarrow Q$
"You have a password", P
Therefore − "You can log on to facebook"
Modus Tollens
If $P \rightarrow Q$ and $\lnot Q$ are two premises, we can use Modus Tollens to derive $\lnot P$.
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$
Example
"If you have a password, then you can log on to facebook", $P \rightarrow Q$
"You cannot log on to facebook", $\lnot Q$
Therefore − "You do not have a password "
Disjunctive Syllogism
If $\lnot P$ and $P \lor Q$ are two premises, we can use Disjunctive Syllogism to derive Q.
$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$
Example
"The ice cream is not vanilla flavored", $\lnot P$
"The ice cream is either vanilla flavored or chocolate flavored", $P \lor Q$
Therefore − "The ice cream is chocolate flavored”
Hypothetical Syllogism
If $P \rightarrow Q$ and $Q \rightarrow R$ are two premises, we can use Hypothetical Syllogism to derive $P \rightarrow R$
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$
Example
"If it rains, I shall not go to school”, $P \rightarrow Q$
"If I don't go to school, I won't need to do homework", $Q \rightarrow R$
Therefore − "If it rains, I won't need to do homework"
Constructive Dilemma
If $( P \rightarrow Q ) \land (R \rightarrow S)$ and $P \lor R$ are two premises, we can use constructive dilemma to derive $Q \lor S$.
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$
Example
“If it rains, I will take a leave”, $( P \rightarrow Q )$
“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$
“Either it will rain or it is hot outside”, $P \lor R$
Therefore − "I will take a leave or I will go for a shower"
Destructive Dilemma
If $(P \rightarrow Q) \land (R \rightarrow S)$ and $ \lnot Q \lor \lnot S $ are two premises, we can use destructive dilemma to derive $\lnot P \lor \lnot R$.
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$
Example
“If it rains, I will take a leave”, $(P \rightarrow Q )$
“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$
“Either I will not take a leave or I will not go for a shower”, $\lnot Q \lor \lnot S$
Therefore − "Either it does not rain or it is not hot outside"
Group Theory is a branch of mathematics and abstract algebra that defines an algebraic structure named as group. Generally, a group comprises of a set of elements and an operation over any two elements on that set to form a third element also in that set.
In 1854, Arthur Cayley, the British Mathematician, gave the modern definition of group for the first time −
“A set of symbols all of them different, and such that the product of any two of them (no matter in what order), or the product of any one of them into itself, belongs to the set, is said to be a group. These symbols are not in general convertible [commutative], but are associative.”
In this chapter, we will know about operators and postulates that form the basics of set theory, group theory and Boolean algebra.
Any set of elements in a mathematical system may be defined with a set of operators and a number of postulates.
A binary operator defined on a set of elements is a rule that assigns to each pair of elements a unique element from that set. For example, given the set $ A = \lbrace 1, 2, 3, 4, 5 \rbrace $, we can say $\otimes$ is a binary operator for the operation $c = a \otimes b$, if it specifies a rule for finding c for the pair of $(a,b)$, such that $a,b,c \in A$.
The postulates of a mathematical system form the basic assumptions from which rules can be deduced. The postulates are −
Closure
A set is closed with respect to a binary operator if for every pair of elements in the set, the operator finds a unique element from that set.
Example
Let $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
This set is closed under binary operator into $(\ast)$, because for the operation $c = a \ast b$, for any $a, b \in A$, the product $c \in A$.
The set is not closed under binary operator divide $(\div)$, because, for the operation $c = a \div b$, for any $a, b \in A$, the product c may not be in the set A. If $a = 7, b = 2$, then $c = 3.5$. Here $a,b \in A$ but $c \notin A$.
Associative Laws
A binary operator $\otimes$ on a set A is associative when it holds the following property −
$(x \otimes y) \otimes z = x \otimes (y \otimes z)$, where $x, y, z \in A $
Example
Let $A = \lbrace 1, 2, 3, 4 \rbrace$
The operator plus $( + )$ is associative because for any three elements, $x,y,z \in A$, the property $(x + y) + z = x + ( y + z )$ holds.
The operator minus $( - )$ is not associative since
$$( x - y ) - z \ne x - ( y - z )$$
Commutative Laws
A binary operator $\otimes$ on a set A is commutative when it holds the following property −
$x \otimes y = y \otimes x$, dónde $x, y \in A$
Ejemplo
Dejar $A = \lbrace 1, 2, 3, 4 \rbrace$
El operador más $( + )$ es conmutativa porque para dos elementos cualesquiera, $x,y \in A$, la propiedad $x + y = y + x$ sostiene.
El operador menos $( - )$ no es asociativo ya que
$$x - y \ne y - x$$
Leyes distributivas
Dos operadores binarios $\otimes$ y $\circledast$ en un conjunto A, son distributivos sobre el operador $\circledast$ cuando se cumple la siguiente propiedad:
$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$, dónde $x, y, z \in A $
Ejemplo
Dejar $A = \lbrace 1, 2, 3, 4 \rbrace$
Los operadores en $( * )$ y mas $( + )$ son distributivos sobre el operador + porque para cualesquiera tres elementos, $x,y,z \in A$, la propiedad $x * ( y + z ) = ( x * y ) + ( x * z )$ sostiene.
Sin embargo, estos operadores no son distributivos $*$ ya que
$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$
Elemento de identidad
Un conjunto A tiene un elemento de identidad con respecto a una operación binaria $\otimes$ en A, si existe un elemento $e \in A$, de modo que se mantenga la siguiente propiedad:
$e \otimes x = x \otimes e$, dónde $x \in A$
Ejemplo
Dejar $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
El elemento 1 es un elemento de identidad con respecto a la operación $*$ ya que para cualquier elemento $x \in Z$,
$$1 * x = x * 1$$
Por otro lado, no existe un elemento de identidad para la operación menos $( - )$
Inverso
Si un conjunto A tiene un elemento de identidad $e$ con respecto a un operador binario $\otimes $, se dice que tiene un inverso siempre que para cada elemento $x \in A$, existe otro elemento $y \in A$, de modo que se mantenga la siguiente propiedad:
$$x \otimes y = e$$
Ejemplo
Dejar $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$
Dada la operación más $( + )$ y $e = 0$, la inversa de cualquier elemento x es $(-x)$ ya que $x + (x) = 0$
Ley de De Morgan
Las leyes de De Morgan dan un par de transformaciones entre la unión y la intersección de dos (o más) conjuntos en términos de sus complementos. Las leyes son ...
$$(A \cup B)' = A' \cap B'$$
$$(A \cap B)' = A' \cup B'$$
Ejemplo
Dejar $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$y
conjunto universal $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$
$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$
$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$
$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$
$A \cap B = \lbrace 1, 3 \rbrace $
$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$
$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$
Por tanto, vemos que $(A \cup B)' = A' \cap B'$
$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
Por tanto, vemos que $(A \cap B)' = A' \cup B'$
Semigroup
Un conjunto finito o infinito $‘S’$ con una operación binaria $‘\omicron’$ (Composición) se llama semigrupo si se cumple siguiendo dos condiciones simultáneamente:
Closure - Para cada par $(a, b) \in S, \:(a \omicron b)$ tiene que estar presente en el set $S$.
Associative - Para cada elemento $a, b, c \in S, (a \omicron b) \omicron c = a \omicron (b \omicron c)$ debe aguantar.
Ejemplo
El conjunto de enteros positivos (excluyendo el cero) con operación de suma es un semigrupo. Por ejemplo,$ S = \lbrace 1, 2, 3, \dots \rbrace $
Aquí la propiedad de cierre se mantiene como para cada par $(a, b) \in S, (a + b)$ está presente en el conjunto S. Por ejemplo, $1 + 2 = 3 \in S]$
La propiedad asociativa también es válida para cada elemento. $a, b, c \in S, (a + b) + c = a + (b + c)$. Por ejemplo,$(1 + 2) + 3 = 1 + (2 + 3) = 5$
Monoide
Un monoide es un semigrupo con un elemento de identidad. El elemento de identidad (denotado por$e$ o E) de un conjunto S es un elemento tal que $(a \omicron e) = a$, para cada elemento $a \in S$. Un elemento de identidad también se denominaunit element. Entonces, un monoide tiene tres propiedades simultáneamente:Closure, Associative, Identity element.
Ejemplo
El conjunto de enteros positivos (excluyendo el cero) con operación de multiplicación es un monoide. $S = \lbrace 1, 2, 3, \dots \rbrace $
Aquí la propiedad de cierre se mantiene como para cada par $(a, b) \in S, (a \times b)$ está presente en el conjunto S. [Por ejemplo, $1 \times 2 = 2 \in S$ y así]
La propiedad asociativa también es válida para cada elemento. $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [Por ejemplo, $(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ y así]
La propiedad de identidad también es válida para cada elemento $a \in S, (a \times e) = a$ [Por ejemplo, $(2 \times 1) = 2, (3 \times 1) = 3$y así]. Aquí el elemento de identidad es 1.
Grupo
Un grupo es un monoide con un elemento inverso. El elemento inverso (denotado por I) de un conjunto S es un elemento tal que$(a \omicron I) = (I \omicron a) = a$, para cada elemento $a \in S$. Entonces, un grupo tiene cuatro propiedades simultáneamente: i) Cierre, ii) Asociativo, iii) Elemento de identidad, iv) Elemento inverso. El orden de un grupo G es el número de elementos en G y el orden de un elemento en un grupo es el número entero menos positivo n tal que an es el elemento de identidad de ese grupo G.
Ejemplos
El conjunto de $N \times N$ las matrices no singulares forman un grupo bajo la operación de multiplicación de matrices.
El producto de dos $N \times N$ matrices no singulares también es un $N \times N$ matriz no singular que tiene la propiedad de cierre.
La multiplicación de matrices en sí es asociativa. Por tanto, la propiedad asociativa se mantiene.
El conjunto de $N \times N$ Las matrices no singulares contienen la matriz de identidad que contiene la propiedad del elemento de identidad.
Como todas las matrices son no singulares, todas tienen elementos inversos que también son matrices no singulares. Por tanto, la propiedad inversa también es válida.
Grupo Abeliano
Un grupo abeliano G es un grupo para el cual el par de elementos $(a,b) \in G$siempre mantiene la ley conmutativa. Entonces, un grupo tiene cinco propiedades simultáneamente: i) Cierre, ii) Asociativo, iii) Elemento de identidad, iv) Elemento inverso, v) Conmutativo.
Ejemplo
El conjunto de enteros positivos (incluido el cero) con operación de suma es un grupo abeliano. $G = \lbrace 0, 1, 2, 3, \dots \rbrace$
Aquí la propiedad de cierre se mantiene como para cada par $(a, b) \in S, (a + b)$ está presente en el conjunto S. [Por ejemplo, $1 + 2 = 2 \in S$ y así]
La propiedad asociativa también es válida para cada elemento. $a, b, c \in S, (a + b) + c = a + (b + c)$ [Por ejemplo, $(1 +2) + 3 = 1 + (2 + 3) = 6$ y así]
La propiedad de identidad también es válida para cada elemento $a \in S, (a \times e) = a$ [Por ejemplo, $(2 \times 1) = 2, (3 \times 1) = 3$y así]. Aquí, el elemento de identidad es 1.
La propiedad conmutativa también es válida para cada elemento. $a \in S, (a \times b) = (b \times a)$ [Por ejemplo, $(2 \times 3) = (3 \times 2) = 3$ y así]
Grupo y subgrupo cíclicos
UN cyclic groupes un grupo que puede ser generado por un solo elemento. Cada elemento de un grupo cíclico es una potencia de algún elemento específico que se llama generador. Un grupo cíclico puede ser generado por un generador 'g', de modo que todos los demás elementos del grupo pueden escribirse como una potencia del generador 'g'.
Ejemplo
El conjunto de números complejos $\lbrace 1,-1, i, -i \rbrace$ bajo operación de multiplicación es un grupo cíclico.
Hay dos generadores: $i$ y $–i$ como $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ y también $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$que cubre todos los elementos del grupo. Por tanto, es un grupo cíclico.
Note - A cyclic groupes siempre un grupo abeliano, pero no todos los grupos abelianos son cíclicos. Los números racionales bajo la suma no son cíclicos sino abelianos.
UN subgroup H es un subconjunto de un grupo G (denotado por $H ≤ G$) si satisface las cuatro propiedades simultáneamente - Closure, Associative, Identity elementy Inverse.
Un subgrupo H de un grupo G que no incluye a todo el grupo G se denomina subgrupo adecuado (denotado por $H < G$). Un subgrupo de un grupo cíclico es cíclico y un subgrupo abeliano también es abeliano.
Ejemplo
Deja un grupo $G = \lbrace 1, i, -1, -i \rbrace$
Entonces algunos subgrupos son $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,
Este no es un subgrupo - $H_3 = \lbrace 1, i \rbrace$ por eso $(i)^{-1} = -i$ no está dentro $H_3$
Conjunto parcialmente ordenado (POSET)
Un conjunto parcialmente ordenado consiste en un conjunto con una relación binaria que es reflexiva, antisimétrica y transitiva. "Conjunto parcialmente ordenado" se abrevia como POSET.
Ejemplos
El conjunto de números reales bajo operación binaria menor o igual a $(\le)$ es un poset.
Deja el set $S = \lbrace 1, 2, 3 \rbrace$ y la operación es $\le$
Las relaciones serán $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$
Esta relación R es reflexiva como $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$
Esta relación R es antisimétrica, ya que
$\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ and\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉ R$
Esta relación R también es transitiva como $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$.
Por tanto, es un poset.
El conjunto de vértices de un gráfico acíclico dirigido bajo la operación 'alcanzabilidad' es un poset.
Diagrama de Hasse
El diagrama de Hasse de un poset es el gráfico dirigido cuyos vértices son el elemento de ese poset y los arcos cubren los pares (x, y) en el poset. Si en el poset$x < y$, entonces el punto x aparece más bajo que el punto y en el diagrama de Hasse. Si$x<y<z$ en el poset, entonces la flecha no se muestra entre xyz ya que está implícita.
Ejemplo
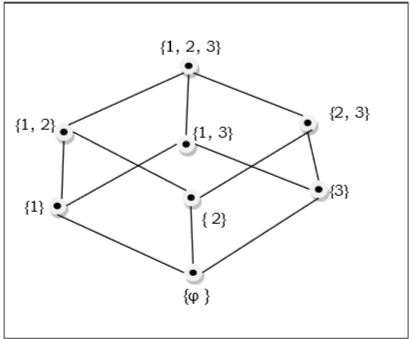
El conjunto de subconjuntos de $\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ se muestra en el siguiente diagrama de Hasse:
Conjunto ordenado linealmente
Un conjunto ordenado linealmente o un conjunto ordenado total es un conjunto de orden parcial en el que cada par de elementos es comparable. Los elementos$a, b \in S$ se dice que son comparables si $a \le b$ o $b \le a$sostiene. La ley de tricotomía define este conjunto ordenado total. Un conjunto totalmente ordenado se puede definir como una red distributiva que tiene la propiedad$\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ para todos los valores de ayb en el conjunto S.
Ejemplo
El poder de $\lbrace a, b \rbrace$ ordenado por \ subseteq es un conjunto totalmente ordenado como todos los elementos del conjunto de potencias $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b\rbrace \rbrace$ son comparables.
Ejemplo de conjunto de pedidos no totales
Un conjunto $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ bajo la operación x divide y no es un conjunto ordenado total.
Aquí para todos $(x, y) \in S, x | y$tienen que aguantar pero no es cierto que 2 | 3, como 2 no divide a 3 o 3 no divide a 2. Por lo tanto, no es un conjunto ordenado total.
Enrejado
Una celosía es un poset $(L, \le)$ por lo que cada par $\lbrace a, b \rbrace \in L$ tiene un límite superior mínimo (denotado por $a \lor b$) y un límite inferior más grande (denotado por $a \land b$). LUB$(\lbrace a,b \rbrace)$se llama la unión de ay b. GLB$(\lbrace a,b \rbrace )$ se llama el encuentro de ay b.
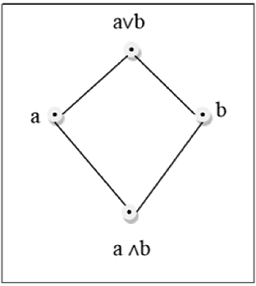
Ejemplo
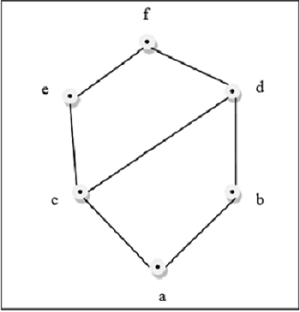
Esta figura anterior es una celosía porque para cada par $\lbrace a, b \rbrace \in L$, existe un GLB y un LUB.
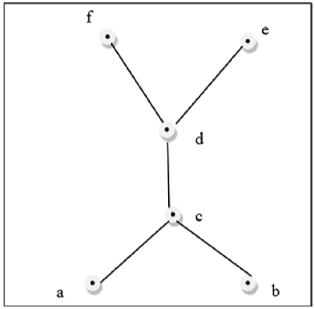
Esta figura anterior no es una celosía porque $GLB (a, b)$ y $LUB (e, f)$ no existe.
Algunas otras celosías se analizan a continuación:
Celosía acotada
Una celosía L se convierte en una celosía acotada si tiene un elemento mayor 1 y un elemento mínimo 0.
Celosía complementada
Una celosía L se convierte en una celosía complementada si es una celosía acotada y si cada elemento de la celosía tiene un complemento. Un elemento x tiene un complemento x 'si$\exists x(x \land x’=0 and x \lor x’ = 1)$
Celosía distributiva
Si un retículo satisface las siguientes dos propiedades de distribución, se denomina retículo distributivo.
$a \lor (b \land c) = (a \lor b) \land (a \lor c)$
$a \land (b \lor c) = (a \land b) \lor (a \land c)$
Celosía modular
Si una celosía satisface la siguiente propiedad, se denomina celosía modular.
$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$
Propiedades de las celosías
Propiedades idempotentes
$a \lor a = a$
$a \land a = a$
Propiedades de absorción
$a \lor (a \land b) = a$
$a \land (a \lor b) = a$
Propiedades conmutativas
$a \lor b = b \lor a$
$a \land b = b \land a$
Propiedades asociativas
$a \lor (b \lor c) = (a \lor b) \lor c$
$a \land (b \land c) = (a \land b) \land c$
Doble de una celosía
El dual de una celosía se obtiene intercambiando el '$\lor$'y'$\land$'operaciones.
Ejemplo
El dual de $\lbrack a \lor (b \land c) \rbrack\ is\ \lbrack a \land (b \lor c) \rbrack$
En la vida diaria, muchas veces es necesario averiguar el número de todos los resultados posibles para una serie de eventos. Por ejemplo, ¿de cuántas formas se puede elegir un panel de jueces compuesto por 6 hombres y 4 mujeres entre 50 hombres y 38 mujeres? ¿Cuántos números PAN de 10 letras diferentes se pueden generar de modo que las primeras cinco letras sean letras mayúsculas, las cuatro siguientes sean dígitos y la última sea nuevamente una letra mayúscula? Para resolver estos problemas se utiliza la teoría matemática del conteo.Counting Abarca principalmente la regla de conteo fundamental, la regla de permutación y la regla de combinación.
Las reglas de suma y producto
los Rule of Sum y Rule of Product se utilizan para descomponer problemas de conteo difíciles en problemas simples.
The Rule of Sum - Si una secuencia de tareas $T_1, T_2, \dots, T_m$ se puede hacer en $w_1, w_2, \dots w_m$ formas respectivamente (la condición es que no se puedan realizar tareas simultáneamente), entonces el número de formas de realizar una de estas tareas es $w_1 + w_2 + \dots +w_m$. Si consideramos dos tareas A y B que son inconexas (es decir,$A \cap B = \emptyset$), luego matemáticamente $|A \cup B| = |A| + |B|$
The Rule of Product - Si una secuencia de tareas $T_1, T_2, \dots, T_m$ se puede hacer en $w_1, w_2, \dots w_m$ formas respectivamente y cada tarea llega después de la ocurrencia de la tarea anterior, entonces hay $w_1 \times w_2 \times \dots \times w_m$formas de realizar las tareas. Matemáticamente, si una tarea B llega después de una tarea A, entonces$|A \times B| = |A|\times|B|$
Ejemplo
Question- Un niño vive en X y quiere ir a la escuela en Z. Desde su casa X primero tiene que llegar a Y y luego de Y a Z. Puede ir de X a Y por 3 rutas de autobús o 2 rutas de tren. Desde allí, puede elegir 4 rutas de autobús o 5 rutas de tren para llegar a Z. ¿Cuántas formas hay para ir de X a Z?
Solution - De X a Y, puede entrar $3 + 2 = 5$formas (regla de la suma). A partir de entonces, puede ir de Y a Z en$4 + 5 = 9$formas (regla de la suma). Por lo tanto, de X a Z puede entrar$5 \times 9 = 45$ formas (regla de producto).
Permutaciones
UN permutationes una disposición de algunos elementos en los que el orden importa. En otras palabras, una permutación es una combinación ordenada de elementos.
Ejemplos
De un conjunto S = {x, y, z} tomando dos a la vez, todas las permutaciones son -
$ xy, yx, xz, zx, yz, zy $.
Tenemos que formar una permutación de números de tres dígitos a partir de un conjunto de números. $S = \lbrace 1, 2, 3 \rbrace$. Se formarán diferentes números de tres dígitos cuando organicemos los dígitos. La permutación será = 123, 132, 213, 231, 312, 321
Número de permutaciones
El número de permutaciones de 'n' cosas diferentes tomadas 'r' a la vez se denota por $n_{P_{r}}$
$$n_{P_{r}} = \frac{n!}{(n - r)!}$$
dónde $n! = 1.2.3. \dots (n - 1).n$
Proof - Que haya 'n' elementos diferentes.
Hay n varias formas de ocupar el primer lugar. Después de llenar el primer lugar (n-1) queda el número de elementos. Por tanto, existen (n-1) formas de ocupar el segundo lugar. Después de llenar el primer y segundo lugar, queda (n-2) número de elementos. Por tanto, hay (n-2) formas de ocupar el tercer lugar. Ahora podemos generalizar el número de formas de llenar el r-ésimo lugar como [n - (r – 1)] = n – r + 1
Entonces, el total no. de formas de llenar desde el primer lugar hasta el r-ésimo lugar -
$n_{ P_{ r } } = n (n-1) (n-2)..... (n-r + 1)$
$= [n(n-1)(n-2) ... (n-r + 1)] [(n-r)(n-r-1) \dots 3.2.1] / [(n-r)(n-r-1) \dots 3.2.1]$
Por lo tanto,
$n_{ P_{ r } } = n! / (n-r)!$
Algunas fórmulas importantes de permutación
Si hay n elementos de los cuales$a_1$ son parecidos de algún tipo, $a_2$ son iguales de otro tipo; $a_3$ son iguales de tercer tipo y así sucesivamente y $a_r$ son de $r^{th}$ amable, donde $(a_1 + a_2 + ... a_r) = n$.
Entonces, el número de permutaciones de estos n objetos es = $n! / [(a_1!(a_2!) \dots (a_r!)]$.
Número de permutaciones de n elementos distintos que toman n elementos a la vez = $n_{P_n} = n!$
El número de permutaciones de n elementos diferentes que toman r elementos a la vez, cuando x cosas particulares siempre ocupan lugares definidos = $n-x_{p_{r-x}}$
El número de permutaciones de n elementos diferentes cuando r cosas especificadas siempre se juntan es - $r! (n−r+1)!$
El número de permutaciones de n elementos diferentes cuando r cosas especificadas nunca se juntan es - $n!–[r! (n−r+1)!]$
El número de permutaciones circulares de n elementos diferentes tomados x elementos en el tiempo = $^np_{x}/x$
El número de permutaciones circulares de n cosas diferentes = $^np_{n}/n$
Algunos problemas
Problem 1 - De un montón de 6 cartas diferentes, ¿de cuántas formas podemos permutarlo?
Solution - Como tomamos 6 cartas a la vez de una baraja de 6 cartas, la permutación será $^6P_{6} = 6! = 720$
Problem 2 - ¿De cuántas formas se pueden ordenar las letras de la palabra 'LECTOR'?
Solution - Hay una palabra de 6 letras (2 E, 1 A, 1D y 2R.) En la palabra 'LECTOR'.
La permutación será $= 6! /\: [(2!) (1!)(1!)(2!)] = 180.$
Problem 3 - ¿De qué manera se pueden ordenar las letras de la palabra 'NARANJA' de modo que las consonantes ocupen sólo las posiciones pares?
Solution- Hay 3 vocales y 3 consonantes en la palabra 'NARANJA'. Número de formas de ordenar las consonantes entre sí.$= ^3P_{3} = 3! = 6$. Los 3 lugares vacantes restantes se llenarán con 3 vocales en$^3P_{3} = 3! = 6$formas. Por tanto, el número total de permutación es$6 \times 6 = 36$
Combinaciones
UN combination es la selección de algunos elementos dados en cuyo orden no importa.
El número de todas las combinaciones de n cosas, tomadas r a la vez es -
$$^nC_{ { r } } = \frac { n! } { r!(n-r)! }$$
Problem 1
Encuentra el número de subconjuntos del conjunto $\lbrace1, 2, 3, 4, 5, 6\rbrace$ que tiene 3 elementos.
Solution
La cardinalidad del conjunto es 6 y tenemos que elegir 3 elementos del conjunto. Aquí, el orden no importa. Por lo tanto, el número de subconjuntos será$^6C_{3} = 20$.
Problem 2
Hay 6 hombres y 5 mujeres en una habitación. ¿De cuántas formas podemos elegir 3 hombres y 2 mujeres de la habitación?
Solution
El número de formas de elegir 3 hombres de 6 hombres es $^6C_{3}$ y el número de formas de elegir 2 mujeres de 5 mujeres es $^5C_{2}$
Por lo tanto, el número total de formas es: $^6C_{3} \times ^5C_{2} = 20 \times 10 = 200$
Problem 3
¿De cuántas formas puede elegir 3 grupos distintos de 3 estudiantes de un total de 9 estudiantes?
Solution
Numeremos los grupos como 1, 2 y 3
Para elegir 3 estudiantes para el 1er grupo, el número de formas -$^9C_{3}$
El número de formas de elegir 3 estudiantes para el 2 ° grupo después de elegir el 1 ° grupo -$^6C_{3}$
El número de formas para la elección de 3 estudiantes de 3 er grupo después de la elección de 1 st y 2 nd grupo -$^3C_{3}$
Por lo tanto, el número total de formas $= ^9C_{3} \times ^6C_{3} \times ^3C_{3} = 84 \times 20 \times 1 = 1680$
Identidad de Pascal
Identidad de Pascal, primera derivada por Blaise Pascal en 17 º siglo, los estados que el número de maneras para elegir k elementos de n elementos es igual a la suma de número de maneras para elegir elementos (k-1) de (1 n-) elementos y el número de formas de elegir elementos de n-1 elementos.
Matemáticamente, para cualquier número entero positivo kyn: $^nC_{k} = ^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$
Proof -
$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$
$= \frac{ (n-1)! } { (k-1)!(n-k)! } + \frac{ (n-1)! } { k!(n-k-1)! }$
$= (n-1)!(\frac{ k } { k!(n-k)! } + \frac{ n-k } { k!(n-k)! } )$
$= (n-1)! \frac{ n } { k!(n-k)! }$
$= \frac{ n! } { k!(n-k)! }$
$= n_{ C_{ k } }$
Principio del casillero
En 1834, el matemático alemán Peter Gustav Lejeune Dirichlet estableció un principio al que llamó principio del cajón. Ahora, se conoce como el principio del casillero.
Pigeonhole Principleestablece que si hay menos casilleros que el número total de palomas y cada paloma se coloca en un casillero, entonces debe haber al menos un casillero con más de una paloma. Si se ponen n palomas en m casilleros donde n> m, hay un agujero con más de una paloma.
Ejemplos
Diez hombres están en una habitación y participan en un apretón de manos. Si cada persona da la mano al menos una vez y ningún hombre da la mano al mismo hombre más de una vez, entonces dos hombres participaron en el mismo número de apretones de manos.
Debe haber al menos dos personas en una clase de 30 cuyos nombres comiencen con el mismo alfabeto.
El principio de inclusión-exclusión
los Inclusion-exclusion principlecalcula el número cardinal de la unión de múltiples conjuntos no disjuntos. Para dos conjuntos A y B, el principio establece:
$|A \cup B| = |A| + |B| - |A \cap B|$
Para tres conjuntos A, B y C, el principio establece:
$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$
La fórmula generalizada -
$|\bigcup_{i=1}^{n}A_i|=\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\pi-1}|A_1 \cap \dots \cap A_2|$
Problem 1
¿Cuántos números enteros del 1 al 50 son múltiplos de 2 o 3 pero no ambos?
Solution
De 1 a 100, hay $50/2 = 25$ números que son múltiplos de 2.
Existen $50/3 = 16$ números que son múltiplos de 3.
Existen $50/6 = 8$ números que son múltiplos de 2 y 3.
Entonces, $|A|=25$, $|B|=16$ y $|A \cap B|= 8$.
$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$
Problem 2
En un grupo de 50 estudiantes, a 24 les gustan las bebidas frías ya 36 les gustan las bebidas calientes, y a cada estudiante le gusta al menos una de las dos bebidas. ¿A cuántos les gusta tanto el café como el té?
Solution
Sea X el conjunto de estudiantes a los que les gustan las bebidas frías e Y sea el conjunto de personas a las que les gustan las bebidas calientes.
Entonces, $| X \cup Y | = 50$, $|X| = 24$, $|Y| = 36$
$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 60 - 50 = 10$
Por lo tanto, hay 10 estudiantes a los que les gusta tanto el té como el café.
Muy relacionado con los conceptos de contar está la probabilidad. A menudo tratamos de adivinar los resultados de los juegos de azar, como juegos de cartas, máquinas tragamonedas y loterías; es decir, tratamos de encontrar la probabilidad de que se obtenga un resultado particular.
Probabilitypuede conceptualizarse como encontrar la posibilidad de que ocurra un evento. Matemáticamente, es el estudio de procesos aleatorios y sus resultados. Las leyes de la probabilidad tienen una amplia aplicabilidad en una variedad de campos como la genética, el pronóstico del tiempo, las encuestas de opinión, los mercados de valores, etc.
Conceptos básicos
La teoría de la probabilidad fue inventada en el siglo XVII por dos matemáticos franceses, Blaise Pascal y Pierre de Fermat, que se ocupaban de problemas matemáticos relacionados con el azar.
Antes de pasar a los detalles de la probabilidad, obtengamos el concepto de algunas definiciones.
Random Experiment- Un experimento en el que se conocen todos los resultados posibles y el resultado exacto no se puede predecir de antemano se denomina experimento aleatorio. Lanzar una moneda justa es un ejemplo de experimento aleatorio.
Sample Space- Cuando realizamos un experimento, entonces el conjunto S de todos los resultados posibles se denomina espacio muestral. Si lanzamos una moneda, el espacio muestral$S = \left \{ H, T \right \}$
Event- Cualquier subconjunto de un espacio muestral se denomina evento. Después de lanzar una moneda, conseguir que Head esté en la cima es un evento.
La palabra "probabilidad" significa la posibilidad de que ocurra un evento en particular. Lo mejor que podemos decir es la probabilidad de que sucedan, utilizando la idea de probabilidad.
$Probability\:of\:occurence\:of\:an\:event = \frac{Total\:number\:of\:favourable \: outcome}{Total\:number\:of\:Outcomes}$
Como la ocurrencia de cualquier evento varía entre 0% y 100%, la probabilidad varía entre 0 y 1.
Pasos para encontrar la probabilidad
Paso 1: calcula todos los resultados posibles del experimento.
Paso 2: calcula el número de resultados favorables del experimento.
Paso 3: aplique la fórmula de probabilidad correspondiente.
Tirando una moneda
Si se lanza una moneda, hay dos resultados posibles: Cara $(H)$ o colas $(T)$
Entonces, número total de resultados = 2
Por lo tanto, la probabilidad de obtener una cabeza $(H)$ en la parte superior es 1/2 y la probabilidad de obtener un Colas $(T)$ en la parte superior es 1/2
Lanzar un dado
Cuando se lanza un dado, se pueden encontrar seis resultados posibles en la parte superior: $1, 2, 3, 4, 5, 6$.
La probabilidad de cualquiera de los números es 1/6
La probabilidad de obtener números pares es 3/6 = 1/2
La probabilidad de obtener números impares es 3/6 = 1/2
Sacar cartas de una baraja
De una baraja de 52 cartas, si se elige una, calcule la probabilidad de que se saque un as y también la probabilidad de que se saque un diamante.
Número total de resultados posibles: 52
Resultados de ser un as - 4
Probabilidad de ser un as = 4/52 = 1/13
Probabilidad de ser un diamante = 13/52 = 1/4
Axiomas de probabilidad
La probabilidad de un evento siempre varía de 0 a 1. $[0 \leq P(x) \leq 1]$
Para un evento imposible, la probabilidad es 0 y para cierto evento la probabilidad es 1.
Si la ocurrencia de un evento no está influenciada por otro evento, se denominan mutuamente excluyentes o disjuntos.
Si $A_1, A_2....A_n$ son eventos mutuamente excluyentes / disjuntos, entonces $P(A_i \cap A_j) = \emptyset $ para $i \ne j$ y $P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$
Propiedades de la probabilidad
Si hay dos eventos $x$ y $\overline{x}$que son complementarios, entonces la probabilidad del evento complementario es -
$$p(\overline{x}) = 1-p(x)$$
Para dos eventos A y B no disjuntos, la probabilidad de la unión de dos eventos -
$P(A \cup B) = P(A) + P(B)$
Si un evento A es un subconjunto de otro evento B (es decir, $A \subset B$), entonces la probabilidad de A es menor o igual que la probabilidad de B. Por lo tanto, $A \subset B$ implica $P(A) \leq p(B)$
La probabilidad condicional
La probabilidad condicional de un evento B es la probabilidad de que el evento ocurra dado que un evento A ya ha ocurrido. Esto está escrito como$P(B|A)$.
Matemáticamente - $ P(B|A) = P(A \cap B)/ P(A)$
Si el evento A y B son mutuamente excluyentes, entonces la probabilidad condicional del evento B después del evento A será la probabilidad del evento B que es $P(B)$.
Problem 1
En un país, el 50% de todos los adolescentes tienen una bicicleta y el 30% de todos los adolescentes tienen una bicicleta y una bicicleta. ¿Cuál es la probabilidad de que un adolescente sea dueño de una bicicleta dado que el adolescente tiene una bicicleta?
Solution
Supongamos que A es el caso de los adolescentes que solo tienen una bicicleta y B es el caso de que los adolescentes solo tienen una bicicleta.
Entonces, $P(A) = 50/100 = 0.5$ y $P(A \cap B) = 30/100 = 0.3$ del problema dado.
$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$
Por lo tanto, la probabilidad de que un adolescente sea dueño de una bicicleta dado que el adolescente posee una bicicleta es del 60%.
Problem 2
En una clase, el 50% de todos los estudiantes juegan al cricket y el 25% de todos los estudiantes juegan al cricket y al voleibol. ¿Cuál es la probabilidad de que un estudiante juegue voleibol dado que el estudiante juega al cricket?
Solution
Supongamos que A es el evento de estudiantes que juegan solo críquet y B es el evento de estudiantes que juegan solo voleibol.
Entonces, $P(A) = 50/100 =0.5$ y $P(A \cap B) = 25/ 100 =0.25$ del problema dado.
$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$
Por lo tanto, la probabilidad de que un estudiante juegue voleibol dado que el estudiante juega críquet es del 50%.
Problem 3
Se mezclan seis computadoras portátiles buenas y tres defectuosas. Para encontrar las computadoras portátiles defectuosas, todas se prueban uno por uno al azar. ¿Cuál es la probabilidad de encontrar las dos computadoras portátiles defectuosas en las dos primeras selecciones?
Solution
Sea A el caso de que encontremos una computadora portátil defectuosa en la primera prueba y B sea el evento de que encontremos una computadora portátil defectuosa en la segunda prueba.
Por lo tanto, $P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$
Teorema de Bayes
Theorem - Si A y B son dos eventos mutuamente excluyentes, donde $P(A)$ es la probabilidad de A y $P(B)$ es la probabilidad de B, $P(A | B)$ es la probabilidad de A dado que B es verdadera. $P(B | A)$ es la probabilidad de B dado que A es verdadera, entonces el teorema de Bayes establece:
$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$
Aplicación del teorema de Bayes
En situaciones donde todos los eventos del espacio muestral son eventos mutuamente excluyentes.
En situaciones en las que $P( A_i \cap B )$ para cada $A_i$ o $P( A_i )$ y $P(B|A_i)$ para cada $A_i$ es conocida.
Problem
Considere tres soportes para bolígrafos. El primer portalápices contiene 2 bolígrafos rojos y 3 bolígrafos azules; el segundo tiene 3 bolígrafos rojos y 2 bolígrafos azules; y el tercero tiene 4 bolígrafos rojos y 1 bolígrafo azul. Existe la misma probabilidad de que se seleccione cada portalápices. Si se saca un bolígrafo al azar, ¿cuál es la probabilidad de que sea un bolígrafo rojo?
Solution
Dejar $A_i$caso de que se seleccione el i- ésimo portalápices.
Aquí, i = 1,2,3.
Dado que la probabilidad de elegir un portalápices es igual, $P(A_i) = 1/3$
Sea B el evento de que se dibuje una pluma roja.
La probabilidad de que se elija un bolígrafo rojo entre los cinco bolígrafos del primer portalápices,
$P(B|A_1) = 2/5$
La probabilidad de que se elija un bolígrafo rojo entre los cinco bolígrafos del segundo portalápices,
$P(B|A_2) = 3/5$
La probabilidad de que se elija un bolígrafo rojo entre los cinco bolígrafos del tercer portalápices,
$P(B|A_3) = 4/5$
Según el teorema de Bayes,
$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$
$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$
$= 3/5$
Mathematical induction, es una técnica para probar resultados o establecer declaraciones para números naturales. Esta parte ilustra el método a través de una variedad de ejemplos.
Definición
Mathematical Induction es una técnica matemática que se utiliza para demostrar que un enunciado, una fórmula o un teorema es verdadero para cada número natural.
La técnica implica dos pasos para probar una declaración, como se indica a continuación:
Step 1(Base step) - Prueba que una afirmación es verdadera para el valor inicial.
Step 2(Inductive step)- Demuestra que si la afirmación es verdadera para la enésima iteración (o el número n ), entonces también lo es para (n + 1) la iteración (o el número n + 1 ).
Cómo hacerlo
Step 1- Considere un valor inicial para el que la afirmación es verdadera. Debe demostrarse que la afirmación es verdadera para n = valor inicial.
Step 2- Suponga que la afirmación es verdadera para cualquier valor de n = k . Luego demuestre que el enunciado es verdadero para n = k + 1 . De hecho, dividimos n = k + 1 en dos partes, una parte es n = k (que ya está probada) y tratamos de probar la otra parte.
Problema 1
$3^n-1$ es un múltiplo de 2 para n = 1, 2, ...
Solution
Step 1 - para $n = 1, 3^1-1 = 3-1 = 2$ que es un múltiplo de 2
Step 2 - Asumamos $3^n-1$ es cierto para $n=k$, Por lo tanto, $3^k -1$ es cierto (es una suposición)
Tenemos que demostrar que $3^{k+1}-1$ también es múltiplo de 2
$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$
La primera parte $(2 \times 3k)$ seguramente será un múltiplo de 2 y la segunda parte $(3k -1)$ también es cierto como nuestra suposición anterior.
Por lo tanto, $3^{k+1} – 1$ es un múltiplo de 2.
Entonces, está probado que $3^n – 1$ es un múltiplo de 2.
Problema 2
$1 + 3 + 5 + ... + (2n-1) = n^2$ para $n = 1, 2, \dots $
Solution
Step 1 - para $n=1, 1 = 1^2$Por tanto, se cumple el paso 1.
Step 2 - Supongamos que la afirmación es verdadera para $n=k$.
Por lo tanto, $1 + 3 + 5 + \dots + (2k-1) = k^2$ es cierto (es una suposición)
Tenemos que demostrar que $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ también sostiene
$1 + 3 + 5 + \dots + (2(k+1) - 1)$
$= 1 + 3 + 5 + \dots + (2k+2 - 1)$
$= 1 + 3 + 5 + \dots + (2k + 1)$
$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$
$= k^2 + (2k + 1)$
$= (k + 1)^2$
Entonces, $1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ mantener lo que satisface el paso 2.
Por lo tanto, $1 + 3 + 5 + \dots + (2n - 1) = n^2$ está probado.
Problema 3
Pruebalo $(ab)^n = a^nb^n$ es cierto para cada número natural $n$
Solution
Step 1 - para $n=1, (ab)^1 = a^1b^1 = ab$Por tanto, se cumple el paso 1.
Step 2 - Supongamos que la afirmación es verdadera para $n=k$, Por lo tanto, $(ab)^k = a^kb^k$ es cierto (es una suposición).
Tenemos que demostrar que $(ab)^{k+1} = a^{k+1}b^{k+1}$ también sostenga
Dado, $(ab)^k = a^k b^k$
O, $(ab)^k (ab) = (a^k b^k ) (ab)$ [Multiplicar ambos lados por 'ab']
O, $(ab)^{k+1} = (aa^k) ( bb^k)$
O, $(ab)^{k+1} = (a^{k+1}b^{k+1})$
Por tanto, se prueba el paso 2.
Entonces, $(ab)^n = a^nb^n$ es cierto para todo número natural n.
Inducción fuerte
La inducción fuerte es otra forma de inducción matemática. A través de esta técnica de inducción, podemos demostrar que una función proposicional,$P(n)$ es cierto para todos los enteros positivos, $n$, siguiendo los siguientes pasos:
Step 1(Base step) - Prueba que la propuesta inicial $P(1)$ cierto.
Step 2(Inductive step) - Demuestra que la declaración condicional $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ es cierto para enteros positivos $k$.
En este capítulo, discutiremos cómo las técnicas recursivas pueden derivar secuencias y usarse para resolver problemas de conteo. El procedimiento para encontrar los términos de una secuencia de manera recursiva se llamarecurrence relation. Estudiamos la teoría de las relaciones de recurrencia lineal y sus soluciones. Finalmente, presentamos funciones generadoras para resolver relaciones de recurrencia.
Definición
Una relación de recurrencia es una ecuación que define de manera recursiva una secuencia donde el siguiente término es una función de los términos anteriores (Expresando $F_n$ como una combinación de $F_i$ con $i < n$).
Example - Serie Fibonacci - $F_n = F_{n-1} + F_{n-2}$, Torre de Hanoi - $F_n = 2F_{n-1} + 1$
Relaciones de recurrencia lineal
Una ecuación de recurrencia lineal de grado k u orden k es una ecuación de recurrencia que tiene el formato $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k} $($A_n$ es una constante y $A_k \neq 0$) en una secuencia de números como polinomio de primer grado.
Estos son algunos ejemplos de ecuaciones de recurrencia lineal:
| Relaciones de recurrencia | Valores iniciales | Soluciones |
|---|---|---|
| F norte = F norte-1 + F norte-2 | a 1 = a 2 = 1 | Número de Fibonacci |
| F norte = F norte-1 + F norte-2 | una 1 = 1, una 2 = 3 | Número de Lucas |
| F norte = F norte-2 + F norte-3 | una 1 = una 2 = una 3 = 1 | Secuencia de Padovan |
| F n = 2F n-1 + F n-2 | una 1 = 0, una 2 = 1 | Número Pell |
Cómo resolver la relación de recurrencia lineal
Supongamos que una relación de recurrencia lineal de dos ordenados es: $F_n = AF_{n-1} +BF_{n-2}$ donde A y B son números reales.
La ecuación característica para la relación de recurrencia anterior es:
$$x^2 - Ax - B = 0$$
Pueden ocurrir tres casos al encontrar las raíces:
Case 1 - Si esta ecuación se factoriza como $(x- x_1)(x- x_1) = 0$ y produce dos raíces reales distintas $x_1$ y $x_2$, luego $F_n = ax_1^n+ bx_2^n$es la solucion. [Aquí, ayb son constantes]
Case 2 - Si esta ecuación se factoriza como $(x- x_1)^2 = 0$ y produce una sola raíz real $x_1$, luego $F_n = a x_1^n+ bn x_1^n$ es la solucion.
Case 3 − If the equation produces two distinct complex roots, $x_1$ and $x_2$ in polar form $x_1 = r \angle \theta$ and $x_2 = r \angle(- \theta)$, then $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ is the solution.
Problem 1
Solve the recurrence relation $F_n = 5F_{n-1} - 6F_{n-2}$ where $F_0 = 1$ and $F_1 = 4$
Solution
The characteristic equation of the recurrence relation is −
$$x^2 - 5x + 6 = 0,$$
So, $(x - 3) (x - 2) = 0$
Hence, the roots are −
$x_1 = 3$ and $x_2 = 2$
The roots are real and distinct. So, this is in the form of case 1
Hence, the solution is −
$$F_n = ax_1^n + bx_2^n$$
Here, $F_n = a3^n + b2^n\ (As\ x_1 = 3\ and\ x_2 = 2)$
Therefore,
$1 = F_0 = a3^0 + b2^0 = a+b$
$4 = F_1 = a3^1 + b2^1 = 3a+2b$
Solving these two equations, we get $ a = 2$ and $b = -1$
Hence, the final solution is −
$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$
Problem 2
Solve the recurrence relation − $F_n = 10F_{n-1} - 25F_{n-2}$ where $F_0 = 3$ and $F_1 = 17$
Solution
The characteristic equation of the recurrence relation is −
$$ x^2 - 10x -25 = 0$$
So $(x - 5)^2 = 0$
Hence, there is single real root $x_1 = 5$
As there is single real valued root, this is in the form of case 2
Hence, the solution is −
$F_n = ax_1^n + bnx_1^n$
$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$
$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$
Solving these two equations, we get $a = 3$ and $b = 2/5$
Hence, the final solution is − $F_n = 3.5^n +( 2/5) .n.2^n $
Problem 3
Solve the recurrence relation $F_n = 2F_{n-1} - 2F_{n-2}$ where $F_0 = 1$ and $F_1 = 3$
Solution
The characteristic equation of the recurrence relation is −
$$x^2 -2x -2 = 0$$
Hence, the roots are −
$x_1 = 1 + i$ and $x_2 = 1 - i$
In polar form,
$x_1 = r \angle \theta$ and $x_2 = r \angle(- \theta),$ where $r = \sqrt 2$ and $\theta = \frac{\pi}{4}$
The roots are imaginary. So, this is in the form of case 3.
Hence, the solution is −
$F_n = (\sqrt 2 )^n (a cos(n .\sqcap /4) + b sin(n .\sqcap /4))$
$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\sqcap /4) + b sin(0 .\sqcap /4) ) = a$
$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\sqcap /4) + b sin(1 . \sqcap /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$
Solving these two equations we get $a = 1$ and $b = 2$
Hence, the final solution is −
$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$
Non-Homogeneous Recurrence Relation and Particular Solutions
A recurrence relation is called non-homogeneous if it is in the form
$F_n = AF_{n-1} + BF_{n-2} + f(n)$ where $f(n) \ne 0$
Its associated homogeneous recurrence relation is $F_n = AF_{n–1} + BF_{n-2}$
The solution $(a_n)$ of a non-homogeneous recurrence relation has two parts.
First part is the solution $(a_h)$ of the associated homogeneous recurrence relation and the second part is the particular solution $(a_t)$.
$$a_n=a_h+a_t$$
Solution to the first part is done using the procedures discussed in the previous section.
To find the particular solution, we find an appropriate trial solution.
Let $f(n) = cx^n$ ; let $x^2 = Ax + B$ be the characteristic equation of the associated homogeneous recurrence relation and let $x_1$ and $x_2$ be its roots.
If $x \ne x_1$ and $x \ne x_2$, then $a_t = Ax^n$
If $x = x_1$, $x \ne x_2$, then $a_t = Anx^n$
If $x = x_1 = x_2$, then $a_t = An^2x^n$
Example
Let a non-homogeneous recurrence relation be $F_n = AF_{n–1} + BF_{n-2} + f(n)$ with characteristic roots $x_1 = 2$ and $x_2 = 5$. Trial solutions for different possible values of $f(n)$ are as follows −