Teoría de grafos: conjuntos independientes

Los conjuntos independientes se representan en conjuntos, en los que

• no debería haber any edges adjacent to each other. No debe haber ningún vértice común entre dos aristas.

• no debería haber any vertices adjacent to each other. No debería haber ningún borde común entre dos vértices.

Conjunto de líneas independientes

Sea 'G' = (V, E) una gráfica. Un subconjunto L de E se llama un conjunto de líneas independientes de 'G' si no hay dos bordes en L adyacentes. Este conjunto se denomina conjunto de líneas independientes.

Example

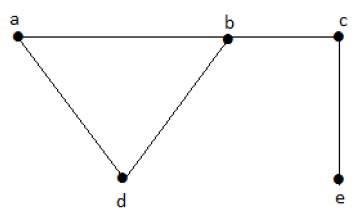
Consideremos los siguientes subconjuntos:

L1 = {a,b}
L2 = {a,b} {c,e}
L3 = {a,d} {b,c}

En este ejemplo, los subconjuntos L2 y L3 claramente no son los bordes adyacentes en el gráfico dado. Son conjuntos de líneas independientes. Sin embargo, L1 no es un conjunto de líneas independiente, ya que para hacer un conjunto de líneas independiente, debe haber al menos dos bordes.

Conjunto de líneas independientes máximas

Se dice que un conjunto de líneas independientes es el conjunto de líneas independientes máximo de un gráfico 'G' si no se puede agregar ningún otro borde de 'G' a 'L'.

Example

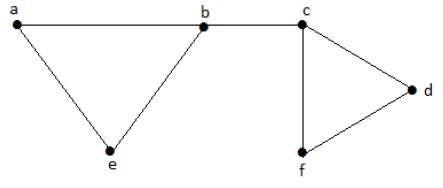
Consideremos los siguientes subconjuntos:

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₂ y L ₃ son conjuntos de líneas independientes máximos / coincidencia máxima. En cuanto a solo estos dos subconjuntos, no hay posibilidad de agregar ningún otro borde que no sea adyacente. Por lo tanto, estos dos subconjuntos se consideran los conjuntos de líneas independientes máximos.

Conjunto máximo de líneas independientes

Un conjunto de líneas independientes máximo de 'G' con el número máximo de bordes se denomina conjunto de líneas independientes máximo de 'G'.

Number of edges in a maximum independent line set of G (β1)
   = Line independent number of G
   = Matching number of G

Example

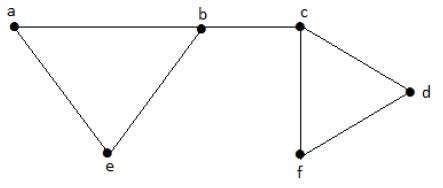
Consideremos los siguientes subconjuntos:

L1 = {a, b}
L2 = {{b, e}, {c, f}}
L3 = {{a, e}, {b, c}, {d, f}}
L4 = {{a, b}, {c, f}}

L ₃ es el conjunto máximo de líneas independientes de G con bordes máximos que no son los bordes adyacentes en el gráfico y se denota por β1 = 3.

Note - Para cualquier gráfico G sin vértice aislado,

α1 + β1 = número de vértices en un gráfico = | V |

Example

Línea que cubre el número de K _n / C _n / w _n ,

$$ \ alpha 1 = \ lceil \ frac {n} {2} \ rceil \ begin {cases} \ frac {n} {2} \: si \: n \: es \: par \\\ frac {n + 1} {2} \: si \: n \: es \: impar \ end {casos} $$

Número independiente de la línea (Número coincidente) = β ₁ = [n / 2] α ₁ + β ₁ = n.

Conjunto de vértices independientes

Sea 'G' = (V, E) una gráfica. Un subconjunto de 'V' se denomina conjunto independiente de 'G' si no hay dos vértices en 'S' adyacentes.

Example

Considere los siguientes subconjuntos de los gráficos anteriores:

S1 = {e}

S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Claramente, S ₁ no es un conjunto de vértices independientes, porque para obtener un conjunto de vértices independientes, debe haber al menos dos vértices en el de un gráfico. Pero aquí no es ese caso. Los subconjuntos S ₂ , S ₃ y S ₄ son los conjuntos de vértices independientes porque no hay vértice adyacente a ningún vértice de los subconjuntos.

Conjunto de vértices independientes máximo

Sea 'G' un gráfico, entonces se dice que un conjunto de vértices independientes de 'G' es máximo si no se puede agregar ningún otro vértice de 'G' a 'S'.

Example

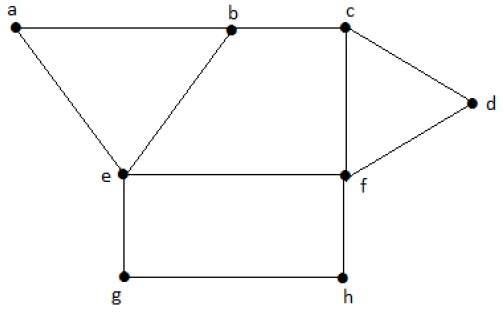
Considere los siguientes subconjuntos de los gráficos anteriores.

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

S ₂ y S ₃ son conjuntos máximos de vértices independientes de 'G'. En S ₁ y S ₄ , podemos agregar otros vértices; pero en S ₂ y S ₃ , no podemos agregar ningún otro vértice.

Máximo conjunto de vértices independientes

Un conjunto de vértices independientes máximo de 'G' con el número máximo de vértices se denomina conjunto de vértices independientes máximo.

Example

Considere los siguientes subconjuntos del gráfico anterior:

S1 = {e}
S2 = {e, f}
S3 = {a, g, c}
S4 = {e, d}

Solo S ₃ es el máximo conjunto de vértices independientes, ya que cubre el mayor número de vértices. El número de vértices en un conjunto máximo de vértices independientes de 'G' se denomina número de vértices independientes de G (β ₂ ).

Example

Para el gráfico completo K _n ,

Número de cobertura del vértice = α ₂ = n − 1

Número independiente del vértice = β ₂ = 1

Tienes α ₂ + β ₂ = n

En un gráfico completo, cada vértice es adyacente a sus vértices restantes (n - 1). Por lo tanto, un conjunto máximo independiente de K _n contiene solo un vértice.

Por lo tanto, β ₂ = 1

y α ₂ = | v | - β ₂ = n-1

Note - Para cualquier gráfico 'G' = (V, E)

• α ₂ + β ₂ = | v |
• Si 'S' es un conjunto de vértices independientes de 'G', entonces (V - S) es una cubierta de vértice de G.