Teoría de grafos - Isomorfismo
Un gráfico puede existir en diferentes formas con el mismo número de vértices, aristas y también la misma conectividad de aristas. Estos gráficos se denominan gráficos isomorfos. Tenga en cuenta que etiquetamos los gráficos en este capítulo principalmente con el propósito de hacer referencia a ellos y reconocerlos entre sí.
Gráficos isomorfos
Se dice que dos gráficos G 1 y G 2 son isomórficos si:
Su número de componentes (vértices y aristas) es el mismo.
Se conserva su conectividad de borde.
Note- En resumen, de los dos gráficos isomórficos, uno es una versión modificada del otro. Un gráfico sin etiquetar también se puede considerar como un gráfico isomorfo.
There exists a function ‘f’ from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.Note
Si G 1 ≡ G 2 entonces -
| V (G 1 ) | = | V (G 2 ) |
| E (G 1 ) | = | E (G 2 ) |
Las secuencias de grados de G 1 y G 2 son iguales.
Si los vértices {V 1 , V 2 , .. Vk} forman un ciclo de longitud K en G 1 , entonces los vértices {f (V 1 ), f (V 2 ),… f (Vk)} deberían formar un ciclo de longitud K en G 2 .
Todas las condiciones anteriores son necesarias para que los gráficos G 1 y G 2 sean isomorfos, pero no suficientes para demostrar que los gráficos son isomorfos.
(G 1 ≡ G 2 ) si y solo si (G 1 - ≡ G 2 -) donde G 1 y G 2 son gráficos simples.
(G 1 ≡ G 2 ) si las matrices de adyacencia de G 1 y G 2 son iguales.
(G 1 ≡ G 2 ) si y solo si los subgrafos correspondientes de G 1 y G 2 (obtenidos al eliminar algunos vértices en G1 y sus imágenes en el gráfico G 2 ) son isomorfos.
Example
¿Cuáles de las siguientes gráficas son isomórficas?
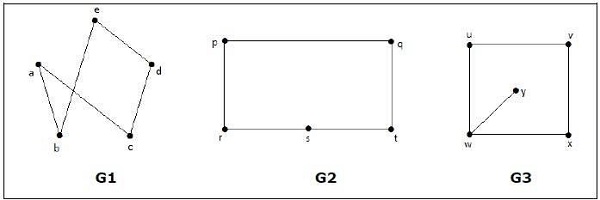
En el gráfico G 3 , el vértice 'w' tiene solo grado 3, mientras que todos los demás vértices del gráfico tienen grado 2. Por lo tanto, G3 no es isomorfo a G 1 o G 2 .
Tomando complementos de G 1 y G 2 , tienes:
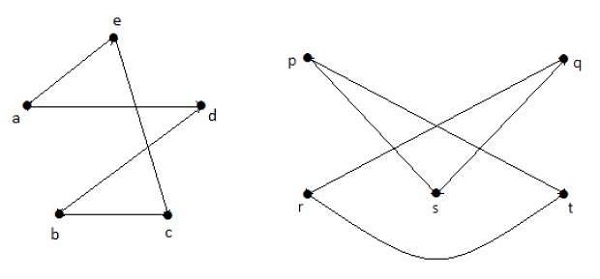
Aquí, (G 1 - ≡ G 2 -), por lo tanto (G 1 ≡ G 2 ).
Gráficos planos
Se dice que una gráfica 'G' es plana si se puede dibujar en un plano o una esfera de modo que no haya dos aristas que se crucen en un punto que no sea vértice.
Example
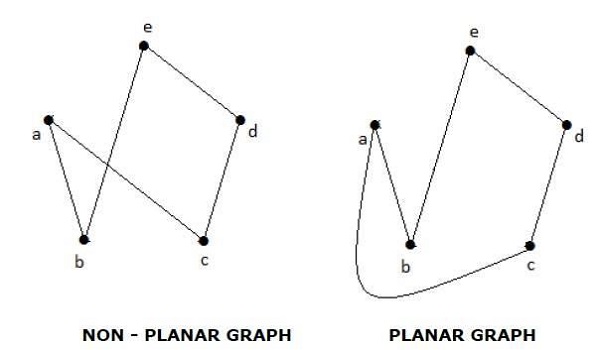
Regiones
Cada gráfico plano divide el plano en áreas conectadas llamadas regiones.
Example
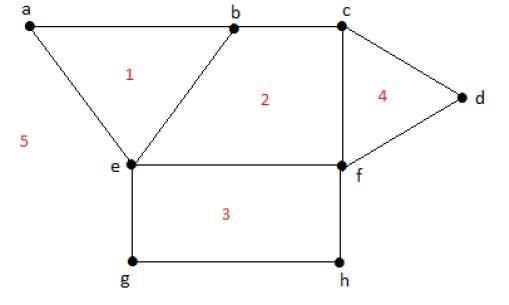
Grado de una región acotada r = deg(r) = Número de aristas que encierran las regiones r.
deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8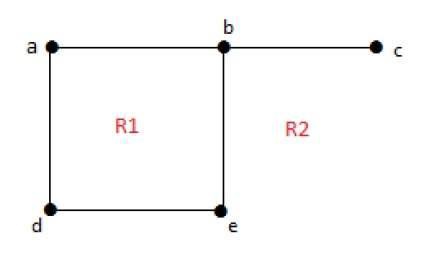
Grado de una región ilimitada r = deg(r) = Número de aristas que encierran las regiones r.
deg(R1) = 4
deg(R2) = 6En gráficos planos, las siguientes propiedades son válidas:
En un gráfico plano con 'n' vértices, la suma de grados de todos los vértices es -
De acuerdo a Sum of Degrees of Regions/ Teorema, en un gráfico plano con 'n' regiones, la suma de grados de regiones es -
Basado en el teorema anterior, puede sacar las siguientes conclusiones:
En un gráfico plano,
Si el grado de cada región es K, entonces la suma de grados de las regiones es -
Si el grado de cada región es al menos K (≥ K), entonces
Si el grado de cada región es como máximo K (≤ K), entonces
Note - Suponga que todas las regiones tienen el mismo grado.
De acuerdo a Euler’s Formulae en gráficos planos,
Si un gráfico 'G' es un plano conectado, entonces
Si una gráfica plana con componentes 'K', entonces
Donde, | V | es el número de vértices, | E | es el número de aristas y | R | es el número de regiones.
Desigualdad de vértice de borde
Si 'G' es un gráfico plano conectado con el grado de cada región al menos 'K' entonces,
| E | ≤ k / (k-2) {| v | - 2}
Ya sabes, | V | + | R | = | E | + 2
K. | R | ≤ 2 | E |
K (| E | - | V | + 2) ≤ 2 | E |
(K - 2) | E | ≤ K (| V | - 2)
| E | ≤ k / (k-2) {| v | - 2}
Si 'G' es un gráfico plano simple conectado, entonces
|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4Existe al menos un vértice V • ∈ G, tal que deg (V) ≤ 5.
Si 'G' es un gráfico plano simple conectado (con al menos 2 aristas) y sin triángulos, entonces
|E| ≤ {2|V| – 4}Teorema de Kuratowski
Un gráfico 'G' no es plano si y solo si 'G' tiene un subgrafo que es homeomorfo a K 5 o K 3,3 .
Homomorfismo
Se dice que dos gráficos G 1 y G 2 son homomórficos, si cada uno de estos gráficos se puede obtener del mismo gráfico 'G' dividiendo algunas aristas de G con más vértices. Eche un vistazo al siguiente ejemplo:

Divida la arista 'rs' en dos aristas agregando un vértice.
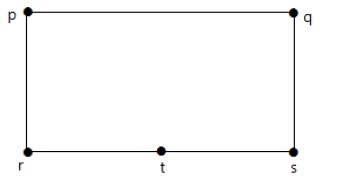
Los gráficos que se muestran a continuación son homomórficos al primer gráfico.
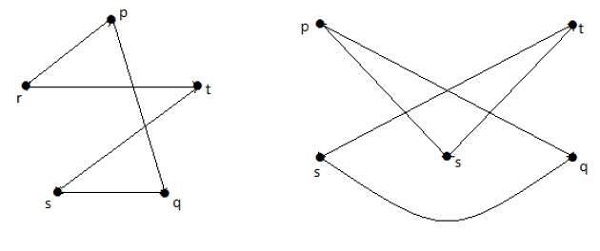
Si G 1 es isomorfo a G 2 , entonces G es homeomorfo a G2 pero no es necesario que lo contrario sea cierto.
Cualquier gráfico con 4 vértices o menos es plano.
Cualquier gráfico con 8 aristas o menos es plano.
Un gráfico completo K n es plano si y solo si n ≤ 4.
El gráfico bipartito completo K m, n es plano si y solo si m ≤ 2 o n ≤ 2.
Un gráfico no plano simple con un número mínimo de vértices es el gráfico completo K 5 .
El gráfico simple no plano con un número mínimo de aristas es K 3, 3 .
Gráfico poliédrico
Una gráfica plana simple conectada se llama gráfica poliédrica si el grado de cada vértice es ≥ 3, es decir, grados (V) ≥ 3 ∀ V ∈ G.
3 | V | ≤ 2 | E |
3 | R | ≤ 2 | E |