Matrices de topología de red

En el capítulo anterior, discutimos cómo convertir un circuito eléctrico en una gráfica equivalente. Ahora, analicemos las matrices de topología de red que son útiles para resolver cualquier problema de red o circuito eléctrico utilizando sus gráficos equivalentes.

Matrices asociadas con gráficos de red

A continuación se muestran las tres matrices que se utilizan en la teoría de grafos.

• Matriz de incidencia
• Matriz de bucle fundamental
• Matriz de conjuntos de corte fundamental

Matriz de incidencia

Una Matriz de Incidencia representa la gráfica de un circuito o red eléctrica dada. Por lo tanto, es posible dibujar la gráfica de ese mismo circuito o red eléctrica a partir de laincidence matrix.

Sabemos que el gráfico consta de un conjunto de nodos y estos están conectados por algunas ramas. Entonces, la conexión de ramas a un nodo se llama incidencia. La matriz de incidencia se representa con la letra A. También se la denomina matriz de incidencia de nodo a rama onode incidence matrix.

Si hay 'n' nodos y 'b' ramas están presentes en un directed graph, entonces la matriz de incidencia tendrá 'n' filas y 'b' columnas. Aquí, las filas y columnas corresponden a los nodos y ramas de un gráfico dirigido. Por lo tanto, laorder de la matriz de incidencia será n × b.

los elements of incidence matrix tendrá uno de estos tres valores, +1, -1 y 0.

• Si la corriente de la rama sale de un nodo seleccionado, entonces el valor del elemento será +1.

• Si la corriente de la rama está entrando hacia un nodo seleccionado, entonces el valor del elemento será -1.

• Si la corriente de la rama no entra en un nodo seleccionado ni sale de un nodo seleccionado, entonces el valor del elemento será 0.

Procedimiento para encontrar la matriz de incidencia

Siga estos pasos para encontrar la matriz de incidencia del gráfico dirigido.

• Seleccione un nodo a la vez del gráfico dirigido dado y llene los valores de los elementos de la matriz de incidencia correspondientes a ese nodo en una fila.

• Repita el paso anterior para todos los nodos del gráfico dirigido dado.

Ejemplo

Considera lo siguiente directed graph.

los incidence matrix correspondiente al gráfico dirigido anteriormente será

$$ A = \ begin {bmatrix} -1 & 1 & 0 & -1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 & -1 \ end {bmatrix} $$

Las filas y columnas de la matriz anterior representan los nodos y ramas de un gráfico dirigido dado. El orden de esta matriz de incidencia es 4 × 6.

Al observar la matriz de incidencia anterior, podemos concluir que la summationde elementos de columna de la matriz de incidencia es igual a cero. Eso significa que una corriente de rama sale de un nodo y entra solo en otro nodo.

Note- Si el gráfico dado es un tipo no dirigido, conviértalo en un gráfico dirigido representando las flechas en cada rama del mismo. Podemos considerar la dirección arbitraria del flujo de corriente en cada rama.

Matriz de bucle fundamental

Bucle fundamental o f-loopes un bucle, que contiene solo un enlace y una o más ramitas. Entonces, el número de f-loops será igual al número de enlaces. La matriz de bucle fundamental se representa con la letra B. También se denomina comofundamental circuit matrixy matriz Tie-set. Esta matriz da la relación entre las corrientes de rama y las corrientes de enlace.

Si hay 'n' nodos y 'b' ramas están presentes en un directed graph, entonces el número de enlaces presentes en un co-árbol, que corresponde al árbol seleccionado del gráfico dado, será b-n + 1.

Entonces, la matriz del ciclo fundamental tendrá filas 'b-n + 1' y columnas 'b'. Aquí, las filas y columnas corresponden a los enlaces del co-árbol y las ramas del gráfico dado. Por lo tanto, el orden de la matriz de bucle fundamental será(b - n + 1) × b.

los elements of fundamental loop matrix tendrá uno de estos tres valores, +1, -1 y 0.

• El valor del elemento será +1 para el enlace del bucle f seleccionado.

• El valor de los elementos será 0 para los enlaces y ramitas restantes, que no forman parte del bucle f seleccionado.

• Si la dirección de la corriente de ramita del bucle f seleccionado es la misma que la de la corriente del enlace del bucle f, entonces el valor del elemento será +1.

• Si la dirección de la corriente de ramitas del bucle f seleccionado es opuesta a la de la corriente del enlace del bucle f, entonces el valor del elemento será -1.

Procedimiento para encontrar la matriz de bucle fundamental

Siga estos pasos para encontrar la matriz de bucle fundamental de un gráfico dirigido dado.

• Seleccione un árbol de gráfico dirigido dado.

• Al incluir un enlace a la vez, obtendremos un f-loop. Llene los valores de los elementos correspondientes a este bucle f en una fila de la matriz del bucle fundamental.

• Repita el paso anterior para todos los enlaces.

Ejemplo

Eche un vistazo al siguiente árbol de directed graph, que se considera para la matriz de incidencia.

El árbol de arriba contiene tres ramas d, e & f. Por tanto, las ramas a, b & c serán los enlaces del Co-Árbol correspondiente al Árbol anterior. Al incluir un enlace a la vez al árbol anterior, obtendremos unof-loop. Entonces, habrá tresf-loops, ya que hay tres enlaces. Estos tres bucles f se muestran en la siguiente figura.

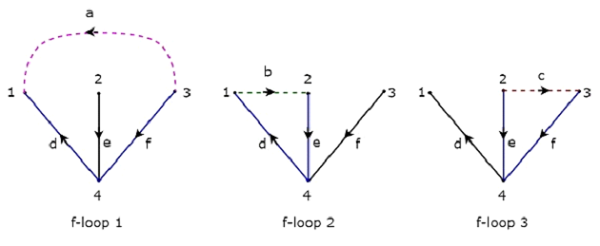
En la figura anterior, las ramas, que están representadas con líneas de colores, forman bucles en F. Obtendremos los valores de los elementos de filas de la matriz Tie-set de cada f-loop. Entonces elTieset matrix del árbol considerado arriba será

$$ B = \ begin {bmatrix} 1 & 0 & 0 & -1 & 0 & -1 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & -1 & 1 \ end {bmatrix} $$

Las filas y columnas de la matriz anterior representan los enlaces y ramas de un gráfico dirigido dado. El orden de esta matriz de incidencia es 3 × 6.

los number of Fundamental loop matricesde una gráfica dirigida será igual al número de árboles de esa gráfica dirigida. Porque, cada árbol tendrá una matriz de bucle fundamental.

Matriz fundamental de conjunto de cortes

Conjunto de corte fundamental o f-cut setes el número mínimo de ramas que se eliminan de un gráfico de tal manera que el gráfico original se convertirá en dos subgráficos aislados. El conjunto f-cut contiene soloone twigy uno o más enlaces. Entonces, el número de conjuntos de cortes en f será igual al número de ramitas.

Fundamental cut set matrix se representa con la letra C. Esta matriz da la relación entre los voltajes de rama y los voltajes de rama.

Si hay 'n' nodos y 'b' ramas están presentes en un directed graph, entonces el número de ramitas presentes en un árbol seleccionado de un gráfico dado será n-1. Entonces, la matriz de conjuntos de corte fundamental tendrá filas 'n-1' y columnas 'b'. Aquí, las filas y columnas corresponden a las ramas del árbol seleccionado y las ramas del gráfico dado. Por lo tanto, laorder de la matriz de conjuntos de corte fundamental será (n-1) × b.

los elements of fundamental cut set matrix tendrá uno de estos tres valores, +1, -1 y 0.

• El valor de element será +1 para la ramita del f-cutset seleccionado.

• El valor de los elementos será 0 para las ramas y eslabones restantes, que no forman parte del conjunto f seleccionado.

• Si la dirección de la corriente de enlace del conjunto de corte f seleccionado es la misma que la de la corriente de ramita del juego de f, entonces el valor del elemento será +1.

• Si la dirección de la corriente de enlace del conjunto de corte f seleccionado es opuesta a la de la corriente de ramita del juego de f, entonces el valor del elemento será -1.

Procedimiento para encontrar la matriz de conjuntos de cortes fundamentales

Siga estos pasos para encontrar la matriz de conjuntos de corte fundamental de un gráfico dirigido dado.

• Seleccione un árbol de un gráfico dirigido dado y represente los enlaces con las líneas de puntos.

• Al quitar una ramita y los enlaces necesarios a la vez, obtendremos un conjunto de corte f. Llene los valores de los elementos correspondientes a este conjunto de corte f en una fila de matriz de conjunto de corte fundamental.

• Repita el paso anterior para todas las ramitas.

Ejemplo

Considere lo mismo directed graph , que discutimos en la sección de matriz de incidencia. Seleccione las ramas d, e & f de este gráfico dirigido como ramitas. Entonces, las ramas restantes a, b & c de este gráfico dirigido serán los enlaces.

los twigs d, e & f se representan con líneas continuas y links a, b & c se representan con líneas de puntos en la siguiente figura.

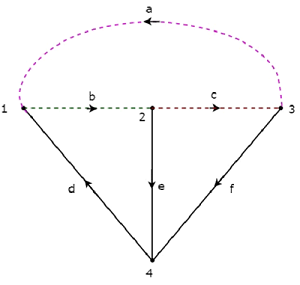
Al quitar una ramita y los enlaces necesarios a la vez, obtendremos un conjunto de corte f. Entonces, habrá tres conjuntos de cortes en f, ya que hay tres ramitas. Estas tresf-cut sets se muestran en la siguiente figura.

Tendremos tres conjuntos de cortes en f quitando un conjunto de ramitas y eslabones de C ₁ , C ₂ y C ₃ . Obtendremos los valores de los elementos de filas de la matriz de conjuntos de cortes fundamentales de cada conjunto de cortes f. Entonces elfundamental cut set matrix del árbol considerado arriba será

$$ C = \ begin {bmatrix} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \ end {bmatrix} $$

Las filas y columnas de la matriz anterior representan las ramas y ramas de un gráfico dirigido dado. El orden de esta matriz de conjuntos de corte fundamental es 3 × 6.

los number of Fundamental cut set matricesde una gráfica dirigida será igual al número de árboles de esa gráfica dirigida. Porque, cada árbol tendrá una matriz de conjunto de corte fundamental.