Assemblage - Introduction
Qu'est-ce que le langage d'assemblage?
Chaque ordinateur personnel possède un microprocesseur qui gère les activités arithmétiques, logiques et de contrôle de l'ordinateur.
Chaque famille de processeurs dispose de son propre ensemble d'instructions pour gérer diverses opérations telles que la saisie à partir du clavier, l'affichage d'informations à l'écran et l'exécution de diverses autres tâches. Cet ensemble d'instructions est appelé «instructions en langage machine».
Un processeur ne comprend que les instructions en langage machine, qui sont des chaînes de 1 et de 0. Cependant, le langage machine est trop obscur et complexe pour être utilisé dans le développement de logiciels. Ainsi, le langage d'assemblage de bas niveau est conçu pour une famille spécifique de processeurs qui représente diverses instructions sous forme de code symbolique et sous une forme plus compréhensible.
Avantages du langage d'assemblage
Avoir une compréhension du langage d'assemblage permet de prendre conscience de -
- L'interface des programmes avec le système d'exploitation, le processeur et le BIOS;
- Comment les données sont représentées dans la mémoire et d'autres périphériques externes;
- Comment le processeur accède et exécute l'instruction;
- Comment les instructions accèdent et traitent les données;
- Comment un programme accède aux périphériques externes.
Les autres avantages de l'utilisation du langage d'assemblage sont:
Cela nécessite moins de mémoire et de temps d'exécution;
Il permet des tâches complexes spécifiques au matériel d'une manière plus simple;
Il convient aux travaux urgents;
Il est le plus approprié pour écrire des routines de service d'interruption et d'autres programmes résidant en mémoire.
Caractéristiques de base du matériel PC
Le matériel interne principal d'un PC se compose du processeur, de la mémoire et des registres. Les registres sont des composants de processeur qui contiennent des données et des adresses. Pour exécuter un programme, le système le copie du périphérique externe dans la mémoire interne. Le processeur exécute les instructions du programme.
L'unité fondamentale de stockage informatique est un peu; il peut être ON (1) ou OFF (0) et un groupe de 8 bits associés fait un octet sur la plupart des ordinateurs modernes.
Ainsi, le bit de parité est utilisé pour rendre le nombre de bits dans un octet impair. Si la parité est égale, le système suppose qu'il y a eu une erreur de parité (bien que rare), qui pourrait avoir été causée par un défaut matériel ou une perturbation électrique.
Le processeur prend en charge les tailles de données suivantes -
- Word: une donnée sur 2 octets
- Mot double: élément de données de 4 octets (32 bits)
- Quadword: un élément de données de 8 octets (64 bits)
- Paragraphe: une zone de 16 octets (128 bits)
- Kilo-octets: 1024 octets
- Mégaoctet: 1 048 576 octets
Système de numération binaire
Chaque système numérique utilise la notation positionnelle, c'est-à-dire que chaque position dans laquelle un chiffre est écrit a une valeur positionnelle différente. Chaque position est la puissance de la base, qui est de 2 pour le système de nombres binaires, et ces puissances commencent à 0 et augmentent de 1.
Le tableau suivant montre les valeurs de position pour un nombre binaire de 8 bits, où tous les bits sont mis à ON.
| Valeur de bit | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|
| Valeur de position en tant que puissance de base 2 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Numéro de bit | sept | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
La valeur d'un nombre binaire est basée sur la présence de 1 bits et leur valeur de position. Ainsi, la valeur d'un nombre binaire donné est -
1 + 2 + 4 + 8 +16 + 32 + 64 + 128 = 255
qui est identique à 2 8 - 1.
Système de nombres hexadécimaux
Le système de nombres hexadécimaux utilise la base 16. Les chiffres de ce système vont de 0 à 15. Par convention, les lettres A à F sont utilisées pour représenter les chiffres hexadécimaux correspondant aux valeurs décimales 10 à 15.
Les nombres hexadécimaux en informatique sont utilisés pour abréger de longues représentations binaires. Fondamentalement, le système de nombre hexadécimal représente une donnée binaire en divisant chaque octet en deux et en exprimant la valeur de chaque demi-octet. Le tableau suivant fournit les équivalents décimaux, binaires et hexadécimaux -
| Nombre décimal | Représentation binaire | Représentation hexadécimale |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | dix | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| sept | 111 | sept |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| dix | 1010 | UNE |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | ré |
| 14 | 1110 | E |
| 15 | 1111 | F |
Pour convertir un nombre binaire en son équivalent hexadécimal, divisez-le en groupes de 4 groupes consécutifs chacun, en commençant par la droite, et écrivez ces groupes sur les chiffres correspondants du nombre hexadécimal.
Example - Le nombre binaire 1000 1100 1101 0001 équivaut à hexadécimal - 8CD1
Pour convertir un nombre hexadécimal en nombre binaire, écrivez simplement chaque chiffre hexadécimal dans son équivalent binaire à 4 chiffres.
Example - Le nombre hexadécimal FAD8 équivaut à binaire - 1111 1010 1101 1000
Arithmétique binaire
Le tableau suivant illustre quatre règles simples pour l'addition binaire -
| (je) | (ii) | (iii) | (iv) |
|---|---|---|---|
| 1 | |||
| 0 | 1 | 1 | 1 |
| +0 | +0 | +1 | +1 |
| = 0 | = 1 | = 10 | = 11 |
Les règles (iii) et (iv) montrent un report de 1 bit dans la position suivante à gauche.
Example
| Décimal | Binaire |
|---|---|
| 60 | 00111100 |
| +42 | 00101010 |
| 102 | 01100110 |
Une valeur binaire négative est exprimée en two's complement notation. Selon cette règle, pour convertir un nombre binaire en sa valeur négative, il faut inverser ses valeurs de bits et ajouter 1 .
Example
| Numéro 53 | 00110101 |
| Inverser les bits | 11001010 |
| Ajouter 1 | 0000000 1 |
| Numéro -53 | 11001011 |
Pour soustraire une valeur d'une autre, convertissez le nombre soustrait au format de complément à deux et ajoutez les nombres .
Example
Soustraire 42 de 53
| Numéro 53 | 00110101 |
| Numéro 42 | 00101010 |
| Inverser les bits de 42 | 11010101 |
| Ajouter 1 | 0000000 1 |
| Numéro -42 | 11010110 |
| 53 - 42 = 11 | 00001011 |
Le débordement du dernier bit est perdu.
Adressage des données en mémoire
Le processus par lequel le processeur contrôle l'exécution des instructions est appelé fetch-decode-execute cycle ou la execution cycle. Il se compose de trois étapes continues -
- Récupérer l'instruction de la mémoire
- Décodage ou identification de l'instruction
- Exécution de l'instruction
Le processeur peut accéder à un ou plusieurs octets de mémoire à la fois. Considérons un nombre hexadécimal 0725H. Ce nombre nécessitera deux octets de mémoire. L'octet de poids fort ou l'octet le plus significatif est 07 et l'octet de poids faible est 25.
Le processeur stocke les données dans une séquence d'octets inversés, c'est-à-dire qu'un octet de poids faible est stocké dans une adresse de mémoire basse et un octet de poids fort dans une adresse de mémoire haute. Ainsi, si le processeur amène la valeur 0725H du registre à la mémoire, il transférera d'abord 25 à l'adresse mémoire inférieure et 07 à l'adresse mémoire suivante.
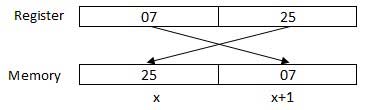
x: adresse mémoire
Lorsque le processeur récupère les données numériques de la mémoire vers le registre, il inverse à nouveau les octets. Il existe deux types d'adresses mémoire -
Adresse absolue - une référence directe d'un emplacement spécifique.
Adresse de segment (ou offset) - adresse de départ d'un segment de mémoire avec la valeur de décalage.