Introduction à la grammaire sans contexte
Definition - Une grammaire sans contexte (CFG) constituée d'un ensemble fini de règles de grammaire est un quadruple (N, T, P, S) où
N est un ensemble de symboles non terminaux.
T est un ensemble de terminaux où N ∩ T = NULL.
P est un ensemble de règles, P: N → (N ∪ T)*, c'est-à-dire le côté gauche de la règle de production P a un contexte droit ou un contexte gauche.
S est le symbole de départ.
Example
- La grammaire ({A}, {a, b, c}, P, A), P: A → aA, A → abc.
- La grammaire ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
- La grammaire ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε
Génération de l'arbre de dérivation
Un arbre de dérivation ou un arbre d'analyse est un arbre enraciné ordonné qui représente graphiquement les informations sémantiques d'une chaîne dérivée d'une grammaire sans contexte.
Technique de représentation
Root vertex - Doit être étiqueté par le symbole de départ.
Vertex - Marqué par un symbole non terminal.
Leaves - étiqueté par un symbole terminal ou ε.
Si S → x 1 x 2 …… x n est une règle de production dans un CFG, alors l'arbre d'analyse / de dérivation sera comme suit -

Il existe deux approches différentes pour dessiner un arbre de dérivation -
Top-down Approach −
Commence par le symbole de départ S
Descend aux feuilles d'arbres en utilisant des productions
Bottom-up Approach −
Commence par les feuilles des arbres
Procède vers le haut jusqu'à la racine qui est le symbole de départ S
Dérivation ou rendement d'un arbre
La dérivation ou le rendement d'un arbre d'analyse est la chaîne finale obtenue en concaténant les étiquettes des feuilles de l'arbre de gauche à droite, en ignorant les Nulls. Cependant, si toutes les feuilles sont nulles, la dérivation est nulle.
Example
Soit un CFG {N, T, P, S}
N = {S}, T = {a, b}, symbole de départ = S, P = S → SS | aSb | ε
Une dérivation du CFG ci-dessus est «abaabb»
S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Forme sententielle et arbre de dérivation partielle
Un arbre de dérivation partielle est un sous-arbre d'un arbre de dérivation / d'un arbre d'analyse tel que soit tous ses enfants sont dans le sous-arbre, soit aucun d'entre eux ne se trouve dans le sous-arbre.
Example
Si dans un CFG les productions sont -
S → AB, A → aaA | ε, B → Bb | ε
l'arbre de dérivation partielle peut être le suivant -
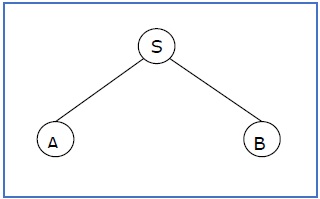
Si un arbre de dérivation partielle contient la racine S, on l'appelle un sentential form. Le sous-arbre ci-dessus est également sous forme sententielle.
Dérivation extrême gauche et droite d'une chaîne
Leftmost derivation - Une dérivation la plus à gauche est obtenue en appliquant la production à la variable la plus à gauche à chaque étape.
Rightmost derivation - Une dérivation la plus à droite est obtenue en appliquant la production à la variable la plus à droite à chaque étape.
Example
Que n'importe quel ensemble de règles de production dans un CFG soit
X → X + X | X * X | X | une
sur un alphabet {a}.
La dérivation la plus à gauche de la chaîne "a+a*a" peut être -
X → X + X → a + X → a + X * X → a + a * X → a + a * a
La dérivation pas à pas de la chaîne ci-dessus est illustrée ci-dessous -

La dérivation la plus à droite pour la chaîne ci-dessus "a+a*a" peut être -
X → X * X → X * a → X + X * a → X + a * a → a + a * a
La dérivation pas à pas de la chaîne ci-dessus est illustrée ci-dessous -

Grammaires récursives gauche et droite
Dans une grammaire sans contexte G, s'il y a une production sous la forme X → Xa où X est un non-terminal et ‘a’ est une chaîne de terminaux, on l'appelle un left recursive production. La grammaire ayant une production récursive à gauche est appeléeleft recursive grammar.
Et si dans une grammaire sans contexte G, s'il y a une production est sous la forme X → aX où X est un non-terminal et ‘a’ est une chaîne de terminaux, on l'appelle un right recursive production. La grammaire ayant une bonne production récursive s'appelle unright recursive grammar.