Automate fini non déterministe

Dans NDFA, pour un symbole d'entrée particulier, la machine peut passer à n'importe quelle combinaison des états de la machine. En d'autres termes, l'état exact dans lequel la machine se déplace ne peut pas être déterminé. Par conséquent, il est appeléNon-deterministic Automaton. Comme elle a un nombre fini d'états, la machine est appeléeNon-deterministic Finite Machine ou Non-deterministic Finite Automaton.

Définition formelle d'un NDFA

Un NDFA peut être représenté par un 5-tuple (Q, ∑, δ, q ₀ , F) où -

Q est un ensemble fini d'états.
∑ est un ensemble fini de symboles appelés alphabets.
δest la fonction de transition où δ: Q × ∑ → 2 ^Q

(Ici, l'ensemble de puissance de Q (2 ^Q ) a été pris car dans le cas de NDFA, à partir d'un état, la transition peut se produire vers n'importe quelle combinaison d'états Q)
q₀est l'état initial à partir duquel toute entrée est traitée (q ₀ ∈ Q).
F est un ensemble d'états finaux de Q (F ⊆ Q).

Représentation graphique d'un NDFA: (identique à DFA)

Un NDFA est représenté par des digraphes appelés diagramme d'état.

Les sommets représentent les états.
Les arcs étiquetés avec un alphabet d'entrée montrent les transitions.
L'état initial est indiqué par un arc entrant unique vide.
L'état final est indiqué par des doubles cercles.

Example

Soit un automate fini non déterministe →

Q = {a, b, c}
∑ = {0, 1}
q ₀ = {a}
F = {c}

La fonction de transition δ comme indiqué ci-dessous -

État actuel	État suivant pour l'entrée 0	État suivant pour l'entrée 1
une	un B	b
b	c	a, c
c	avant JC	c

Sa représentation graphique serait la suivante -

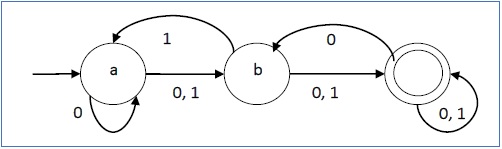
DFA vs NDFA

Le tableau suivant répertorie les différences entre DFA et NDFA.

DFA	NDFA
La transition d'un état est à un état suivant particulier unique pour chaque symbole d'entrée. Par conséquent, il est appelé déterministe .	La transition d'un état peut être vers plusieurs états suivants pour chaque symbole d'entrée. Par conséquent, il est appelé non déterministe .
Les transitions de chaînes vides ne sont pas visibles dans DFA.	NDFA autorise les transitions de chaînes vides.
Le retour en arrière est autorisé dans DFA	Dans NDFA, le retour en arrière n'est pas toujours possible.
Nécessite plus d'espace.	Nécessite moins d'espace.
Une chaîne est acceptée par un DFA, si elle passe à un état final.	Une chaîne est acceptée par un NDFA, si au moins une de toutes les transitions possibles se termine dans un état final.

Accepteurs, classificateurs et transducteurs

Accepteur (reconnaissance)

Un automate qui calcule une fonction booléenne est appelé un acceptor. Tous les états d'un accepteur acceptent ou rejettent les entrées qui lui sont données.

Classificateur

UNE classifier a plus de deux états finaux et il donne une seule sortie quand il se termine.

Transducteur

Un automate qui produit des sorties en fonction de l'entrée actuelle et / ou de l'état précédent est appelé un transducer. Les transducteurs peuvent être de deux types -

Mealy Machine - La sortie dépend à la fois de l'état actuel et de l'entrée courant.
Moore Machine - La sortie dépend uniquement de l'état actuel.

Acceptabilité par DFA et NDFA

Une chaîne est acceptée par un DFA / NDFA ssi le DFA / NDFA commençant à l'état initial se termine dans un état d'acceptation (l'un des états finaux) après la lecture complète de la chaîne.

Une chaîne S est acceptée par un DFA / NDFA (Q, ∑, δ, q ₀ , F), ssi

δ*(q₀, S) ∈ F

La langue L acceptée par DFA / NDFA est

{S | S ∈ ∑* and δ*(q₀, S) ∈ F}

Une chaîne S ′ n'est pas acceptée par un DFA / NDFA (Q, ∑, δ, q ₀ , F), ssi

δ*(q₀, S′) ∉ F

La langue L ′ non acceptée par DFA / NDFA (Complément de la langue acceptée L) est

{S | S ∈ ∑* and δ*(q₀, S) ∉ F}

Example

Prenons le DFA illustré à la figure 1.3. À partir du DFA, les chaînes acceptables peuvent être dérivées.