Apprentissage automatique - Compétences
L'apprentissage automatique a une très grande largeur et nécessite des compétences dans plusieurs domaines. Les compétences que vous devez acquérir pour devenir un expert en apprentissage automatique sont répertoriées ci-dessous:
- Statistics
- Théories des probabilités
- Calculus
- Techniques d'optimisation
- Visualization
Nécessité de diverses compétences d'apprentissage automatique
Pour vous donner une brève idée des compétences que vous devez acquérir, laissez-nous discuter de quelques exemples -
Notation mathématique
La plupart des algorithmes d'apprentissage automatique sont fortement basés sur les mathématiques. Le niveau de mathématiques que vous devez connaître n'est probablement qu'un niveau débutant. Ce qui est important, c'est que vous devriez être capable de lire la notation que les mathématiciens utilisent dans leurs équations. Par exemple, si vous êtes capable de lire la notation et de comprendre ce qu'elle signifie, vous êtes prêt pour l'apprentissage de l'apprentissage automatique. Sinon, vous devrez peut-être rafraîchir vos connaissances en mathématiques.
$$ f_ {AN} (net- \ theta) = \ begin {cases} \ gamma & if \: net- \ theta \ geq \ epsilon \\ net- \ theta & if - \ epsilon <net- \ theta <\ epsilon \\ - \ gamma & if \: net- \ theta \ leq- \ epsilon \ end {cases} $$
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \: label ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ droite), x ^ \ gauche (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
$$ f_ {AN} (net- \ theta) = \ left (\ frac {e ^ {\ lambda (net- \ theta)} - e ^ {- \ lambda (net- \ theta)}} {e ^ { \ lambda (net- \ theta)} + e ^ {- \ lambda (net- \ theta)}} \ right) \; $$
Théorie des probabilités
Voici un exemple pour tester vos connaissances actuelles de la théorie des probabilités: Classification avec des probabilités conditionnelles.
$$ p (c_ {i} | x, y) \; = \ frac {p (x, y | c_ {i}) \; p (c_ {i}) \;} {p (x, y) \ ;} $$
Avec ces définitions, nous pouvons définir la règle de classification bayésienne -
- Si P (c1 | x, y)> P (c2 | x, y), la classe est c1.
- Si P (c1 | x, y) <P (c2 | x, y), la classe est c2.
Problème d'optimisation
Voici une fonction d'optimisation
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \: label ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ droite), x ^ \ gauche (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
Sous réserve des contraintes suivantes -
$$ \ alpha \ geq0 et \: \ displaystyle \ sum \ limits_ {i-1} ^ m \ alpha_ {i} \ cdot \: label ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) = 0 $$
Si vous pouvez lire et comprendre ce qui précède, vous êtes prêt.
Visualisation
Dans de nombreux cas, vous devrez comprendre les différents types de tracés de visualisation pour comprendre la distribution de vos données et interpréter les résultats de la sortie de l'algorithme.
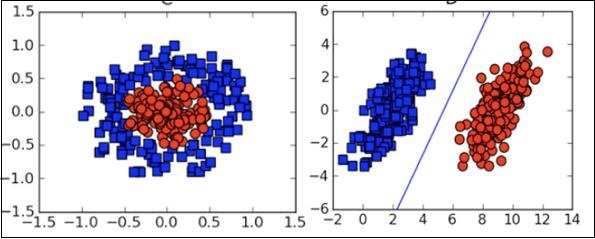
Outre les aspects théoriques ci-dessus de l'apprentissage automatique, vous avez besoin de bonnes compétences en programmation pour coder ces algorithmes.
Alors, que faut-il pour implémenter le ML? Examinons cela dans le chapitre suivant.