Physique - Gravitation
introduction
Tous les corps célestes que l'on trouve dans l'univers s'attirent et la force d'attraction parmi ces corps est appelée gravitational force.

Loi universelle de la gravitation
Chaque objet de l'univers a la propriété d'attirer tous les autres objets avec une force directement proportionnelle au produit de leurs masses et inversement proportionnelle au carré de la distance qui les sépare (voir l'image ci-dessous).
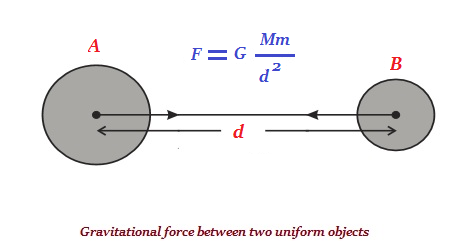
F = force d'attraction entre deux objets 'A' et 'B'
M = masse de 'A'
m = masse de 'B'
d2 = le carré de la distance entre 'A' et 'B'
G = est la constante de proportionnalité et est connue sous le nom de constante de gravitation universelle.
L'unité SI de G est N m2 kg–2. Il est obtenu en substituant les unités de force, de distance et de masse (comme indiqué dans l'équation suivante -
$$ G = \ frac {Fd ^ 2} {M \ fois m} $$
Henry Cavendish avait calculé la valeur de ‘G’ comme 6.673 × 10–11 N m2 kg–2.
Henry Cavendish avait utilisé une balance sensible pour trouver la valeur de «G.»
Signification de la loi universelle de la gravitation
Voici la signification saillante de la loi universelle de la gravitation -
Il explique la force qui lie tous les objets (y compris les êtres humains) à la terre
Il décrit le mouvement de la lune autour de la terre
Il explique le mouvement des planètes autour du Soleil
Il clarifie les marées dues à la lune et au soleil
Chute libre
Chaque fois qu'un objet tombe vers la terre, cela implique une accélération; cette accélération est due à la force gravitationnelle de la terre.

L'accélération, produite en raison de la force gravitationnelle de la Terre, est connue sous le nom d'accélération due à la force gravitationnelle de la Terre (ou accélération due à la gravité).
L'accélération produite en raison de la force gravitationnelle est désignée par g.
Lorsque le rayon de la Terre augmente vers l'équateur (à partir des pôles), la valeur de ‘g’ devient plus grand aux pôles qu'à l'équateur.
La valeur de g
La valeur de g est calculée comme -
$$ g = G \ frac {M} {R ^ 2} $$
G = constante gravitationnelle universelle, qui est = 6.7 × 10–11 N m2 kg-2
M = masse de la terre, qui est = 6 × 1024 kg
R = rayon de la terre, qui est = 6.4 × 106 m
So,
$$ g = \ frac {6,7 \: \ fois 10 ^ {- 11} \: Nm ^ 2 \: kg ^ {- 2} \: \ times \: 6 \: \ times 10 ^ {24} \: kg } {(6,4 \: \ fois 10 ^ 6 \: m) ^ 2} $$
$ = 9,8 \: m \: s ^ {- 2} $
Ainsi, la valeur de l'accélération due à la gravité de la terre (g) est de 9,8 ms -2 .