Physique - Lentilles sphériques
introduction
Un matériau transparent (normalement du verre) lié par deux surfaces, dont une ou les deux surfaces sont sphériques, est appelé «lentille sphérique».

Lentille convexe
Une lentille peut avoir deux surfaces sphériques, bombées vers l'extérieur (comme le montre l'image ci-dessous), est appelée lentille convexe ou lentille double convexe.
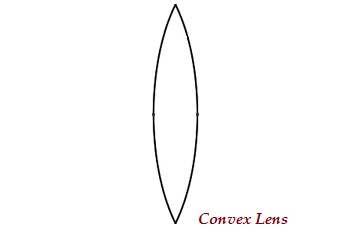
La partie médiane de cette lentille est bombée (plus épaisse) et aux deux extrémités, elle est étroite.
La lentille convexe fait converger les rayons lumineux; par conséquent, il est également connu commeconverging lens.
Lentille concave
Une lentille peut avoir deux surfaces sphériques, incurvées vers l'intérieur (comme le montre l'image ci-dessous), est appelée lentille concave ou lentille double concave.
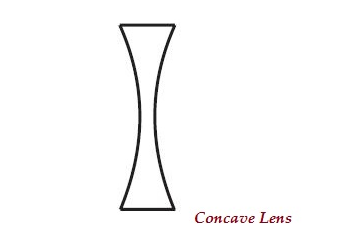
La partie centrale de cette lentille est étroite (courbée vers l'intérieur) et les deux bords sont plus épais.
La lentille concave diverge les rayons lumineux; par conséquent, il est également connu commediverging lens.
Une lentille, concave ou convexe, a deux surfaces sphériques et chacune de ces surfaces fait partie de la sphère. Les centres de ces sphères sont connus commecenters of curvature, représenté par une lettre anglaise 'C».
Comme il y a deux centres de courbure, par conséquent, représentés par «C 1 » et «C 2 ».
Une ligne droite imaginaire, passant par les deux centres de courbure d'une lentille, est connue sous le nom de principal axis.
Le centre optique est le point central d'une lentille. Il est représenté par 'O».
Une ouverture est le diamètre réel du contour circulaire d'une lentille sphérique.
L'objectif principal de la lentille est représenté par 'F».
Une lentille a généralement deux foyers représentés par F 1 et F 2 .
Focal lengthest la distance entre le foyer principal et le centre optique d'une lentille. Il est représenté par 'f».
Le tableau suivant illustre la nature et la position des images formées par une lentille convexe -
| Position de l'objet | Position de l'image | Taille de l'image | Nature de l'image | Image |
|---|---|---|---|---|
| À l'infini | Au foyer F 2 | Très diminué, pointé | Réel et inversé |
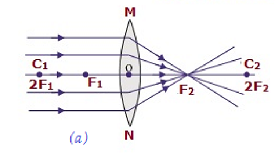
|
| Au-delà de 2F 1 | N / B F 2 et 2F 2 | Diminué | Réel et inversé |
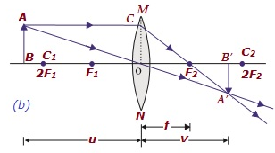
|
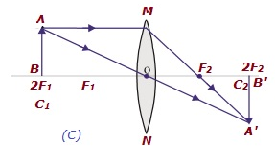
| À 2F 1 | À 2F 2 | Même taille | Réel et inversé |
|
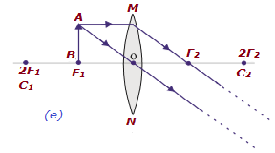
| N / B F 1 et 2F 1 | Au-delà de 2F 2 | Agrandi | Réel et inversé |

|
| Au foyer F 1 | À l'infini | Infiniment grand ou très agrandi | Réel et inverti d |
|
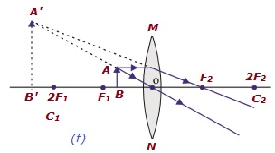
| Mise au point noir et blanc F 1 et centre optique O | Du même côté de l'objectif que l'objet | Agrandi | Virtuel et érigé |
|
Le tableau suivant illustre la nature et la position des images formées par une lentille concave -
| Position de l'objet | Position de l'image | Taille relative de l'image | Nature de l'image | Image |
|---|---|---|---|---|
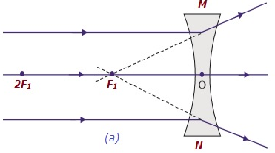
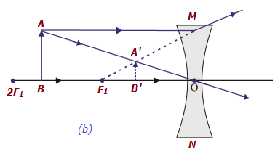
| À l'infini | Au foyer F 1 | Diminue fortement, pointée | Virtuel et érigé |
|
| N / B infini et centre optique O de l'objectif | N / B F 1 & centre optique O | Diminishe d | Virtuel et érigé |
|
Formule de l'objectif
La formule est exprimée comme -
La formule de l'objectif exprime les relations entre l'objet-distance (c.-à-d. u), distance-image (ie v) et la distance focale (c'est-à-dire f) d'un objectif.
$$ \ frac {1} {v} - \ frac {1} {u} = \ frac {1} {f} $$