Tracer des nombres rationnels sur une droite numérique
Un nombre rationnel est une fraction et est tracé sur une droite numérique comme suit.
Basic rules of representing rational no. on number line
Si le nombre rationnel (fraction) est correct, il se situe entre 0 et 1.
Si le n ° rationnel (fraction) est incorrect, nous le convertissons d'abord en fraction mixte, puis le n ° rationnel donné. se situe entre le nombre entier et le nombre entier suivant.
Nous utilisons les étapes suivantes pour représenter un nombre rationnel ou une fraction, par exemple $ \ frac {5} {7} $ sur la droite numérique.
Step 1 - Nous dessinons une droite numérique.
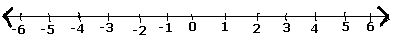
Step 2- Comme le nombre $ \ frac {5} {7} $ est un nombre positif, il se trouve à droite de zéro.
Step 3- Donc, après zéro, nous avons $ \ frac {1} {7}, \: \ frac {2} {7}, \: \ frac {3} {7}, \: \ frac {4} {7 }, \: \ frac {5} {7}, \: \ frac {6} {7}, $ et ( $ \ frac {7} {7} $ = 1).
Step 4- Le nombre rationnel $ \ frac {5} {7} $ sur la droite numérique est représenté comme suit.

Tracez $ \ frac {1} {4} $ et $ 1 \ frac {2} {4} $ sur la droite numérique ci-dessous
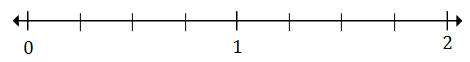
Solution
Step 1:
$ \ frac {1} {4} $ (A) est compris entre 0 et 1; $ 1 \ frac {2} {4} $ (B) est compris entre 1 et 2
Step 2:
Chaque division est divisée en quatre parties car le bas des fractions est 4.
$ \ frac {1} {4} $ est la première marque après 0, donc le point A représente $ \ frac {1} {4} $
$ 1 \ frac {2} {4} $ est la deuxième marque après 1, donc le point B représente $ 1 \ frac {2} {4} $
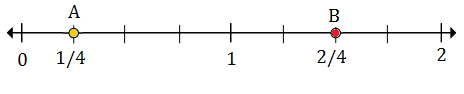
Tracez $ \ frac {5} {8} $ et $ 2 \ frac {3} {8} $ sur la droite numérique ci-dessous
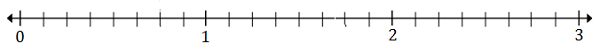
Solution
Step 1:
$ \ frac {5} {8} $ 8 (A) est compris entre 0 et 1; $ 2 \ frac {3} {8} $ (B) est compris entre 2 et 3
Step 2:
Chaque division est divisée en huit parties car le bas des fractions est 8.
$ \ frac {5} {8} $ est la cinquième marque après 0, donc le point A représente $ \ frac {5} {8} $
$ 2 \ frac {3} {8} $ est la troisième marque après 2, donc le point B représente $ 2 \ frac {3} {8} $
