Python Deep Learning - Implémentations

Dans cette mise en œuvre du Deep Learning, notre objectif est de prédire l'attrition des clients ou les données de désabonnement pour une certaine banque - quels clients sont susceptibles de quitter ce service bancaire. L'ensemble de données utilisé est relativement petit et contient 10 000 lignes avec 14 colonnes. Nous utilisons la distribution Anaconda et des frameworks comme Theano, TensorFlow et Keras. Keras est construit sur Tensorflow et Theano qui fonctionnent comme ses backends.

# Artificial Neural Network
# Installing Theano
pip install --upgrade theano

# Installing Tensorflow
pip install –upgrade tensorflow

# Installing Keras
pip install --upgrade keras

Étape 1: prétraitement des données

In[]:

# Importing the libraries
   import numpy as np
   import matplotlib.pyplot as plt
   import pandas as pd
 
# Importing the database
   dataset = pd.read_csv('Churn_Modelling.csv')

Étape 2

Nous créons des matrices des caractéristiques de l'ensemble de données et de la variable cible, qui est la colonne 14, étiquetée comme «Exited».

L'aspect initial des données est comme indiqué ci-dessous -

In[]:
X = dataset.iloc[:, 3:13].values
Y = dataset.iloc[:, 13].values
X

Production

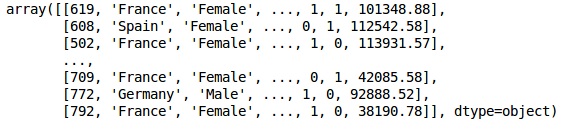
Étape 3

Production

array([1, 0, 1, ..., 1, 1, 0], dtype = int64)

Étape 4

Nous simplifions l'analyse en codant des variables de chaîne. Nous utilisons la fonction ScikitLearn 'LabelEncoder' pour encoder automatiquement les différentes étiquettes dans les colonnes avec des valeurs comprises entre 0 et n_classes-1.

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder() 
X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) 
labelencoder_X_2 = LabelEncoder() 
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
X

Production

Dans la sortie ci-dessus, les noms de pays sont remplacés par 0, 1 et 2; tandis que les hommes et les femmes sont remplacés par 0 et 1.

Étape 5

Labelling Encoded Data

Nous utilisons le même ScikitLearn bibliothèque et une autre fonction appelée OneHotEncoder pour simplement passer le numéro de colonne en créant une variable factice.

onehotencoder = OneHotEncoder(categorical features = [1])
X = onehotencoder.fit_transform(X).toarray()
X = X[:, 1:]
X

Désormais, les 2 premières colonnes représentent le pays et la 4ème colonne représente le sexe.

Production

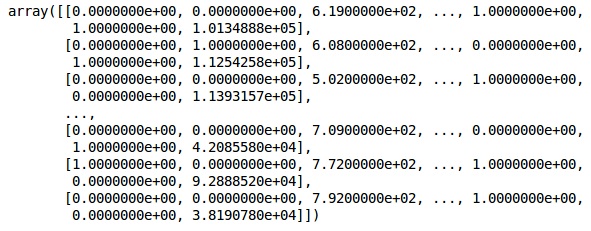
Nous divisons toujours nos données en partie formation et test; nous formons notre modèle sur des données de formation, puis nous vérifions l'exactitude d'un modèle sur des données de test, ce qui aide à évaluer l'efficacité du modèle.

Étape 6

Nous utilisons ScikitLearn train_test_splitfonction pour diviser nos données en ensemble d'entraînement et ensemble de test. Nous conservons le rapport de répartition train-test à 80:20.

#Splitting the dataset into the Training set and the Test Set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

Certaines variables ont des valeurs en milliers tandis que d'autres ont des valeurs en dizaines ou en unités. Nous mettons les données à l'échelle pour qu'elles soient plus représentatives.

Étape 7

Dans ce code, nous ajustons et transformons les données d'entraînement à l'aide du StandardScalerfonction. Nous normalisons notre mise à l'échelle afin d'utiliser la même méthode ajustée pour transformer / mettre à l'échelle les données de test.

# Feature Scaling

fromsklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)

Production

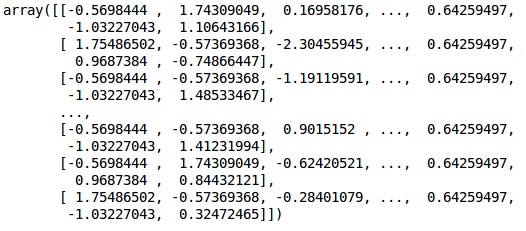
Les données sont désormais correctement mises à l'échelle. Enfin, nous en avons terminé avec notre prétraitement des données. Maintenant, nous allons commencer par notre modèle.

Étape 8

Nous importons ici les modules requis. Nous avons besoin du module Sequential pour initialiser le réseau neuronal et du module dense pour ajouter les couches cachées.

# Importing the Keras libraries and packages 
import keras 
from keras.models import Sequential 
from keras.layers import Dense

Étape 9

Nous nommerons le modèle comme classificateur car notre objectif est de classer le taux de désabonnement des clients. Ensuite, nous utilisons le module Sequential pour l'initialisation.

#Initializing Neural Network 
classifier = Sequential()

Étape 10

Nous ajoutons les couches cachées une par une en utilisant la fonction dense. Dans le code ci-dessous, nous verrons de nombreux arguments.

Notre premier paramètre est output_dim. C'est le nombre de nœuds que nous ajoutons à cette couche.initest l'initialisation du Stochastic Gradient Decent. Dans un réseau neuronal, nous attribuons des pondérations à chaque nœud. Lors de l'initialisation, les poids doivent être proches de zéro et nous initialisons aléatoirement les poids en utilisant la fonction uniforme. leinput_dimLe paramètre n'est nécessaire que pour la première couche, car le modèle ne connaît pas le nombre de nos variables d'entrée. Ici, le nombre total de variables d'entrée est de 11. Dans la deuxième couche, le modèle connaît automatiquement le nombre de variables d'entrée de la première couche cachée.

Exécutez la ligne de code suivante pour ajouter la couche d'entrée et la première couche cachée -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu', input_dim = 11))

Exécutez la ligne de code suivante pour ajouter la deuxième couche cachée -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu'))

Exécutez la ligne de code suivante pour ajouter la couche de sortie -

classifier.add(Dense(units = 1, kernel_initializer = 'uniform', 
activation = 'sigmoid'))

Étape 11

Compiling the ANN

Nous avons ajouté plusieurs couches à notre classificateur jusqu'à présent. Nous allons maintenant les compiler en utilisant lecompileméthode. Les arguments ajoutés dans le contrôle de compilation final complètent le réseau neuronal, nous devons donc faire attention à cette étape.

Voici une brève explication des arguments.

Le premier argument est OptimizerIl s'agit d'un algorithme utilisé pour trouver l'ensemble optimal de poids. Cet algorithme est appelé leStochastic Gradient Descent (SGD). Ici, nous utilisons un parmi plusieurs types, appelé «optimiseur Adam». Le SGD dépend de la perte, notre deuxième paramètre est donc la perte. Si notre variable dépendante est binaire, nous utilisons la fonction de perte logarithmique appelée‘binary_crossentropy’, et si notre variable dépendante a plus de deux catégories en sortie, alors nous utilisons ‘categorical_crossentropy’. Nous voulons améliorer les performances de notre réseau neuronal basé suraccuracy, donc on ajoute metrics comme précision.

# Compiling Neural Network 
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

Étape 12

Un certain nombre de codes doivent être exécutés à cette étape.

Montage de l'ANN sur l'ensemble d'entraînement

Nous formons maintenant notre modèle sur les données d'entraînement. Nous utilisons lefitméthode adaptée à notre modèle. Nous optimisons également les pondérations pour améliorer l'efficacité du modèle. Pour cela, nous devons mettre à jour les poids.Batch size est le nombre d'observations après lequel nous mettons à jour les poids. Epochest le nombre total d'itérations. Les valeurs de la taille du lot et de l'époque sont choisies par la méthode d'essai et d'erreur.

classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)

Faire des prédictions et évaluer le modèle

# Predicting the Test set results
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

Prédire une seule nouvelle observation

# Predicting a single new observation
"""Our goal is to predict if the customer with the following data will leave the bank:
Geography: Spain
Credit Score: 500
Gender: Female
Age: 40
Tenure: 3
Balance: 50000
Number of Products: 2
Has Credit Card: Yes
Is Active Member: Yes

Étape 13

Predicting the test set result

Le résultat de la prédiction vous donnera la probabilité que le client quitte l'entreprise. Nous convertirons cette probabilité en 0 et 1 binaires.

# Predicting the Test set results 
y_pred = classifier.predict(X_test) 
y_pred = (y_pred > 0.5)

new_prediction = classifier.predict(sc.transform
(np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]])))
new_prediction = (new_prediction > 0.5)

Étape 14

C'est la dernière étape où nous évaluons les performances de notre modèle. Nous avons déjà des résultats originaux et nous pouvons donc construire une matrice de confusion pour vérifier l'exactitude de notre modèle.

Making the Confusion Matrix

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print (cm)

Production

loss: 0.3384 acc: 0.8605
[ [1541 54]
[230 175] ]

À partir de la matrice de confusion, la précision de notre modèle peut être calculée comme suit:

Accuracy = 1541+175/2000=0.858

We achieved 85.8% accuracy, ce qui est bon.

L'algorithme de propagation vers l'avant

Dans cette section, nous allons apprendre à écrire du code pour faire une propagation avant (prédiction) pour un simple réseau de neurones -

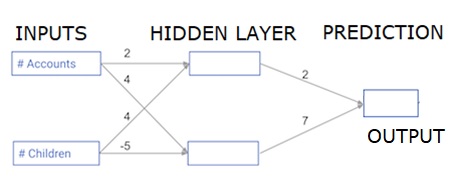
Chaque point de données est un client. La première entrée est le nombre de comptes qu'ils ont et la seconde le nombre d'enfants qu'ils ont. Le modèle prédira le nombre de transactions que l'utilisateur effectuera l'année prochaine.

Les données d'entrée sont préchargées en tant que données d'entrée et les poids sont dans un dictionnaire appelé poids. Le tableau de poids pour le premier nœud de la couche cachée est en poids ['node_0'], et pour le deuxième nœud dans la couche cachée sont respectivement en poids ['node_1'].

Les poids alimentant le nœud de sortie sont disponibles en poids.

La fonction d'activation linéaire rectifiée

Une "fonction d'activation" est une fonction qui fonctionne à chaque nœud. Il transforme l'entrée du nœud en une sortie.

La fonction d'activation linéaire rectifiée (appelée ReLU ) est largement utilisée dans les réseaux à très hautes performances. Cette fonction prend un seul nombre comme entrée, renvoyant 0 si l'entrée est négative et entrée comme sortie si l'entrée est positive.

Voici quelques exemples -

relu (4) = 4
relu (-2) = 0

On remplit la définition de la fonction relu () -

Nous utilisons la fonction max () pour calculer la valeur de la sortie de relu ().
Nous appliquons la fonction relu () à node_0_input pour calculer node_0_output.
Nous appliquons la fonction relu () à node_1_input pour calculer node_1_output.

import numpy as np
input_data = np.array([-1, 2])
weights = {
   'node_0': np.array([3, 3]),
   'node_1': np.array([1, 5]),
   'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)

def relu(input):
   '''Define your relu activation function here'''
   # Calculate the value for the output of the relu function: output
   output = max(input,0)
      # Return the value just calculated
   return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)

# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)

# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])

# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output

Production

0.9950547536867305
-3

Application du réseau à de nombreuses observations / lignes de données

Dans cette section, nous allons apprendre à définir une fonction appelée predict_with_network (). Cette fonction générera des prédictions pour plusieurs observations de données, prises à partir du réseau ci-dessus pris comme input_data. Les poids donnés dans le réseau ci-dessus sont utilisés. La définition de la fonction relu () est également utilisée.

Définissons une fonction appelée predict_with_network () qui accepte deux arguments - input_data_row et weights - et renvoie une prédiction du réseau en sortie.

Nous calculons les valeurs d'entrée et de sortie pour chaque nœud, en les stockant comme: node_0_input, node_0_output, node_1_input et node_1_output.

Pour calculer la valeur d'entrée d'un nœud, nous multiplions les tableaux pertinents ensemble et calculons leur somme.

Pour calculer la valeur de sortie d'un nœud, nous appliquons la fonction relu () à la valeur d'entrée du nœud. Nous utilisons une 'boucle for' pour itérer sur input_data -

Nous utilisons également notre predict_with_network () pour générer des prédictions pour chaque ligne de input_data - input_data_row. Nous ajoutons également chaque prédiction aux résultats.

# Define predict_with_network()
def predict_with_network(input_data_row, weights):
   # Calculate node 0 value
   node_0_input = (input_data_row * weights['node_0']).sum()
   node_0_output = relu(node_0_input)
   
   # Calculate node 1 value
   node_1_input = (input_data_row * weights['node_1']).sum()
   node_1_output = relu(node_1_input)
   
   # Put node values into array: hidden_layer_outputs
   hidden_layer_outputs = np.array([node_0_output, node_1_output])
   
   # Calculate model output
   input_to_final_layer = (hidden_layer_outputs*weights['output']).sum()
   model_output = relu(input_to_final_layer)
# Return model output
   return(model_output)

# Create empty list to store prediction results
results = []
for input_data_row in input_data:
   # Append prediction to results
   results.append(predict_with_network(input_data_row, weights))
print(results)# Print results

Production

[0, 12]

Ici, nous avons utilisé la fonction relu où relu (26) = 26 et relu (-13) = 0 et ainsi de suite.

Réseaux de neurones multicouches profonds

Ici, nous écrivons du code pour faire une propagation avant pour un réseau de neurones avec deux couches cachées. Chaque couche cachée a deux nœuds. Les données d'entrée ont été préchargées commeinput_data. Les nœuds de la première couche masquée sont appelés node_0_0 et node_0_1.

Leurs poids sont préchargés sous forme de poids ['node_0_0'] et de poids ['node_0_1'] respectivement.

Les nœuds de la deuxième couche cachée sont appelés node_1_0 and node_1_1. Leurs poids sont préchargés commeweights['node_1_0'] et weights['node_1_1'] respectivement.

Nous créons ensuite une sortie de modèle à partir des nœuds cachés en utilisant des poids préchargés comme weights['output'].

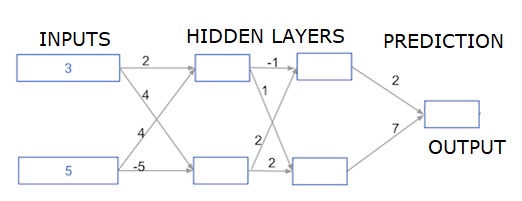
Nous calculons node_0_0_input en utilisant ses poids pondérés ['node_0_0'] et les données d'entrée données. Appliquez ensuite la fonction relu () pour obtenir node_0_0_output.

Nous faisons la même chose que ci-dessus pour node_0_1_input afin d'obtenir node_0_1_output.

Nous calculons node_1_0_input en utilisant ses poids pondérés ['node_1_0'] et les sorties de la première couche cachée - hidden_0_outputs. Nous appliquons ensuite la fonction relu () pour obtenir node_1_0_output.

Nous faisons la même chose que ci-dessus pour node_1_1_input afin d'obtenir node_1_1_output.

Nous calculons model_output en utilisant les poids ['output'] et les sorties du deuxième tableau hidden_1_outputs de la couche cachée. Nous n'appliquons pas la fonction relu () à cette sortie.

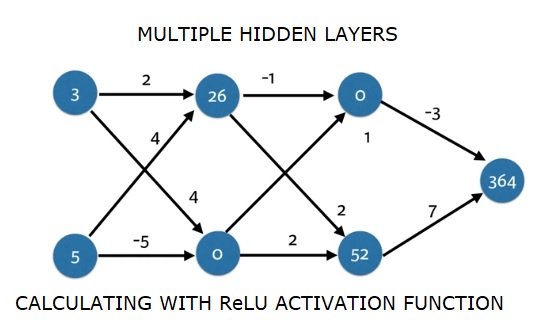
import numpy as np
input_data = np.array([3, 5])
weights = {
   'node_0_0': np.array([2, 4]),
   'node_0_1': np.array([4, -5]),
   'node_1_0': np.array([-1, 1]),
   'node_1_1': np.array([2, 2]),
   'output': np.array([2, 7])
}
def predict_with_network(input_data):
   # Calculate node 0 in the first hidden layer
   node_0_0_input = (input_data * weights['node_0_0']).sum()
   node_0_0_output = relu(node_0_0_input)
   
   # Calculate node 1 in the first hidden layer
   node_0_1_input = (input_data*weights['node_0_1']).sum()
   node_0_1_output = relu(node_0_1_input)
   
   # Put node values into array: hidden_0_outputs
   hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
   
   # Calculate node 0 in the second hidden layer
   node_1_0_input = (hidden_0_outputs*weights['node_1_0']).sum()
   node_1_0_output = relu(node_1_0_input)
   
   # Calculate node 1 in the second hidden layer
   node_1_1_input = (hidden_0_outputs*weights['node_1_1']).sum()
   node_1_1_output = relu(node_1_1_input)
   
   # Put node values into array: hidden_1_outputs
   hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
   
   # Calculate model output: model_output
   model_output = (hidden_1_outputs*weights['output']).sum()
      # Return model_output
   return(model_output)
output = predict_with_network(input_data)
print(output)

Production