Python Deep Learning - Guide rapide

L'apprentissage structuré profond ou l'apprentissage hiérarchique ou l'apprentissage profond en bref fait partie de la famille des méthodes d'apprentissage automatique qui sont elles-mêmes un sous-ensemble du domaine plus large de l'intelligence artificielle.

L'apprentissage en profondeur est une classe d'algorithmes d'apprentissage automatique qui utilisent plusieurs couches d'unités de traitement non linéaires pour l'extraction et la transformation d'entités. Chaque couche successive utilise la sortie de la couche précédente comme entrée.

Les réseaux de neurones profonds, les réseaux de croyances profondes et les réseaux de neurones récurrents ont été appliqués à des domaines tels que la vision par ordinateur, la reconnaissance vocale, le traitement du langage naturel, la reconnaissance audio, le filtrage des réseaux sociaux, la traduction automatique et la bioinformatique où ils ont produit des résultats comparables et dans certains cas. mieux que les experts humains.

Algorithmes et réseaux d'apprentissage profond -

sont basés sur l'apprentissage non supervisé de plusieurs niveaux de caractéristiques ou de représentations des données. Les entités de niveau supérieur sont dérivées d'entités de niveau inférieur pour former une représentation hiérarchique.
utilisez une forme de descente de gradient pour l'entraînement.

Dans ce chapitre, nous allons en apprendre davantage sur l'environnement configuré pour Python Deep Learning. Nous devons installer les logiciels suivants pour créer des algorithmes d'apprentissage en profondeur.

Python 2.7+
Scipy avec Numpy
Matplotlib
Theano
Keras
TensorFlow

Il est fortement recommandé que Python, NumPy, SciPy et Matplotlib soient installés via la distribution Anaconda. Il est livré avec tous ces packages.

Nous devons nous assurer que les différents types de logiciels sont correctement installés.

Allons à notre programme de ligne de commande et saisissez la commande suivante -

$ python
Python 3.6.3 |Anaconda custom (32-bit)| (default, Oct 13 2017, 14:21:34)
[GCC 7.2.0] on linux

Ensuite, nous pouvons importer les bibliothèques requises et imprimer leurs versions -

import numpy
print numpy.__version__

Production

1.14.2

Installation de Theano, TensorFlow et Keras

Avant de commencer l'installation des packages - Theano, TensorFlow et Keras, nous devons confirmer si le pipest installé. Le système de gestion de paquets dans Anaconda s'appelle le pip.

Pour confirmer l'installation de pip, tapez ce qui suit dans la ligne de commande -

$ pip

Une fois l'installation de pip confirmée, nous pouvons installer TensorFlow et Keras en exécutant la commande suivante -

$pip install theano $pip install tensorflow
$pip install keras

Confirmez l'installation de Theano en exécutant la ligne de code suivante -

$python –c “import theano: print (theano.__version__)”

Production

1.0.1

Confirmez l'installation de Tensorflow en exécutant la ligne de code suivante -

$python –c “import tensorflow: print tensorflow.__version__”

Production

1.7.0

Confirmez l'installation de Keras en exécutant la ligne de code suivante -

$python –c “import keras: print keras.__version__”
Using TensorFlow backend

Production

2.1.5

L'intelligence artificielle (IA) est tout code, algorithme ou technique qui permet à un ordinateur d'imiter le comportement cognitif ou l'intelligence humaine. L'apprentissage automatique (ML) est un sous-ensemble de l'IA qui utilise des méthodes statistiques pour permettre aux machines d'apprendre et de s'améliorer avec l'expérience. Le Deep Learning est un sous-ensemble du Machine Learning, qui rend possible le calcul de réseaux de neurones multicouches. L'apprentissage automatique est considéré comme un apprentissage superficiel tandis que l'apprentissage profond est considéré comme un apprentissage hiérarchique avec abstraction.

L'apprentissage automatique traite d'un large éventail de concepts. Les concepts sont listés ci-dessous -

supervised
unsupervised
apprentissage par renforcement
régression linéaire
fonctions de coût
overfitting
under-fitting
hyper-paramètre, etc.

Dans l'apprentissage supervisé, nous apprenons à prédire des valeurs à partir de données étiquetées. Une technique ML qui aide ici est la classification, où les valeurs cibles sont des valeurs discrètes; par exemple, les chats et les chiens. Une autre technique d'apprentissage automatique qui pourrait être utile est la régression. La régression fonctionne sur les valeurs cibles. Les valeurs cibles sont des valeurs continues; par exemple, les données boursières peuvent être analysées à l'aide de la régression.

Dans l'apprentissage non supervisé, nous faisons des inférences à partir des données d'entrée qui ne sont ni étiquetées ni structurées. Si nous avons un million de dossiers médicaux et que nous devons en comprendre le sens, trouver la structure sous-jacente, les valeurs aberrantes ou détecter des anomalies, nous utilisons la technique du clustering pour diviser les données en grands groupes.

Les ensembles de données sont divisés en ensembles de formation, ensembles de tests, ensembles de validation, etc.

Une percée en 2012 a mis en évidence le concept du Deep Learning. Un algorithme a classé 1 million d'images en 1000 catégories avec succès en utilisant 2 GPU et les dernières technologies comme le Big Data.

Relier le Deep Learning et le Machine Learning traditionnel

L'un des principaux défis rencontrés dans les modèles d'apprentissage automatique traditionnels est un processus appelé extraction de fonctionnalités. Le programmeur doit être précis et indiquer à l'ordinateur les fonctionnalités à rechercher. Ces fonctionnalités vous aideront à prendre des décisions.

La saisie de données brutes dans l'algorithme fonctionne rarement, l'extraction de fonctionnalités est donc un élément essentiel du flux de travail traditionnel d'apprentissage automatique.

Cela place une énorme responsabilité sur le programmeur, et l'efficacité de l'algorithme dépend fortement de l'inventivité du programmeur. Pour des problèmes complexes tels que la reconnaissance d'objets ou la reconnaissance de l'écriture manuscrite, il s'agit d'un énorme problème.

L'apprentissage en profondeur, avec la possibilité d'apprendre plusieurs couches de représentation, est l'une des rares méthodes qui nous a aidés à l'extraction automatique de caractéristiques. On peut supposer que les couches inférieures effectuent une extraction automatique des caractéristiques, ne nécessitant que peu ou pas de conseils du programmeur.

Le réseau de neurones artificiels, ou simplement le réseau de neurones, n'est pas une idée nouvelle. Il existe depuis environ 80 ans.

Ce n'est qu'en 2011, lorsque les réseaux de neurones profonds sont devenus populaires grâce à l'utilisation de nouvelles techniques, à l'énorme disponibilité de jeux de données et à des ordinateurs puissants.

Un réseau neuronal imite un neurone, qui a des dendrites, un noyau, un axone et un axone terminal.

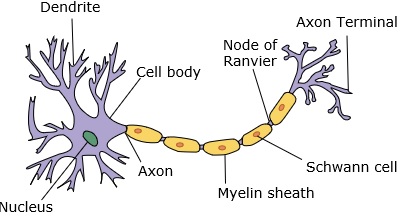
Pour un réseau, nous avons besoin de deux neurones. Ces neurones transfèrent des informations via une synapse entre les dendrites de l'un et l'axone terminal de l'autre.

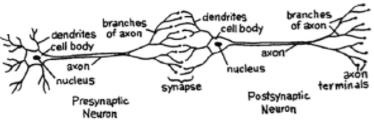
Un modèle probable d'un neurone artificiel ressemble à ceci -

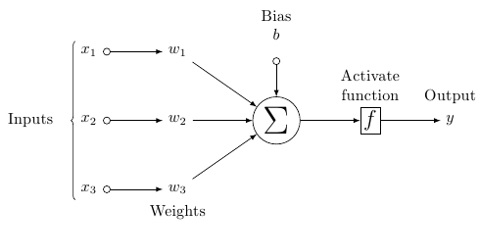
Un réseau de neurones ressemblera à celui ci-dessous -

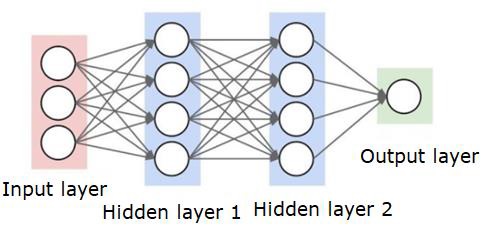
Les cercles sont des neurones ou des nœuds, avec leurs fonctions sur les données et les lignes / arêtes qui les relient sont les poids / informations transmis.

Chaque colonne est une couche. La première couche de vos données est la couche d'entrée. Ensuite, toutes les couches entre la couche d'entrée et la couche de sortie sont les couches cachées.

Si vous avez une ou quelques couches cachées, alors vous avez un réseau neuronal peu profond. Si vous avez de nombreuses couches cachées, vous disposez d'un réseau neuronal profond.

Dans ce modèle, vous avez des données d'entrée, vous les pondérez et les passez à travers la fonction du neurone appelée fonction de seuil ou fonction d'activation.

Fondamentalement, c'est la somme de toutes les valeurs après la comparaison avec une certaine valeur. Si vous déclenchez un signal, le résultat est (1) éteint, ou rien n'est déclenché, alors (0). Cela est ensuite pondéré et transmis au neurone suivant, et le même type de fonction est exécuté.

Nous pouvons avoir une fonction sigmoïde (en forme de S) comme fonction d'activation.

Quant aux poids, ils sont simplement aléatoires au départ, et ils sont uniques par entrée dans le nœud / neurone.

Dans un "feed forward" typique, le type le plus élémentaire de réseau neuronal, vous faites passer vos informations directement à travers le réseau que vous avez créé, et vous comparez la sortie à ce que vous espériez que la sortie aurait utilisé vos exemples de données.

À partir de là, vous devez ajuster les pondérations pour vous aider à faire correspondre votre sortie à la sortie souhaitée.

Le fait d'envoyer des données directement via un réseau neuronal s'appelle un feed forward neural network.

Nos données vont de l'entrée, aux couches, dans l'ordre, puis à la sortie.

Lorsque nous reculons et commençons à ajuster les poids pour minimiser les pertes / coûts, cela s'appelle back propagation.

C'est un optimization problem. Avec le réseau de neurones, en pratique, nous devons faire face à des centaines de milliers de variables, voire des millions, voire plus.

La première solution a été d'utiliser la descente de gradient stochastique comme méthode d'optimisation. Maintenant, il existe des options comme AdaGrad, Adam Optimizer et ainsi de suite. Quoi qu'il en soit, il s'agit d'une opération de calcul massive. C'est pourquoi les réseaux de neurones ont été pour la plupart laissés sur les tablettes pendant plus d'un demi-siècle. Ce n'est que très récemment que nous avons même eu la puissance et l'architecture de nos machines pour même envisager de faire ces opérations, et les jeux de données correctement dimensionnés pour correspondre.

Pour les tâches de classification simples, les performances du réseau neuronal sont relativement proches des autres algorithmes simples tels que K Nearest Neighbours. La véritable utilité des réseaux de neurones se concrétise lorsque nous avons des données beaucoup plus volumineuses et des questions beaucoup plus complexes, qui surpassent les autres modèles d'apprentissage automatique.

Un réseau neuronal profond (DNN) est un ANN avec plusieurs couches cachées entre les couches d'entrée et de sortie. Semblables aux ANNs peu profonds, les DNN peuvent modéliser des relations non linéaires complexes.

L'objectif principal d'un réseau de neurones est de recevoir un ensemble d'entrées, d'effectuer des calculs progressivement complexes sur celles-ci et de fournir une sortie pour résoudre des problèmes du monde réel tels que la classification. Nous nous limitons à alimenter les réseaux de neurones.

Nous avons une entrée, une sortie et un flux de données séquentielles dans un réseau profond.

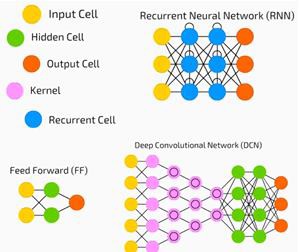
Les réseaux de neurones sont largement utilisés dans les problèmes d'apprentissage supervisé et d'apprentissage par renforcement. Ces réseaux sont basés sur un ensemble de couches connectées les unes aux autres.

Dans l'apprentissage profond, le nombre de couches cachées, pour la plupart non linéaires, peut être important; disons environ 1000 couches.

Les modèles DL produisent de bien meilleurs résultats que les réseaux ML normaux.

Nous utilisons principalement la méthode de descente de gradient pour optimiser le réseau et minimiser la fonction de perte.

Nous pouvons utiliser le Imagenet, un référentiel de millions d'images numériques pour classer un ensemble de données en catégories telles que les chats et les chiens. Les réseaux DL sont de plus en plus utilisés pour les images dynamiques en dehors des images statiques et pour les séries chronologiques et l'analyse de texte.

La formation des ensembles de données constitue une partie importante des modèles de Deep Learning. De plus, Backpropagation est le principal algorithme de formation des modèles DL.

DL traite de la formation de grands réseaux de neurones avec des transformations d'entrée-sortie complexes.

Un exemple de DL est le mappage d'une photo avec le nom de la ou des personnes sur la photo comme ils le font sur les réseaux sociaux et la description d'une image avec une phrase est une autre application récente de DL.

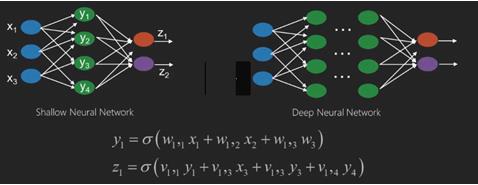
Les réseaux de neurones sont des fonctions qui ont des entrées comme x1, x2, x3… qui sont transformées en sorties comme z1, z2, z3 et ainsi de suite en deux (réseaux peu profonds) ou plusieurs opérations intermédiaires également appelées couches (réseaux profonds).

Les poids et biais changent d'une couche à l'autre. «w» et «v» sont les poids ou synapses des couches des réseaux neuronaux.

Le meilleur cas d'utilisation de l'apprentissage en profondeur est le problème d'apprentissage supervisé. Ici, nous avons un grand ensemble d'entrées de données avec un ensemble de sorties souhaité.

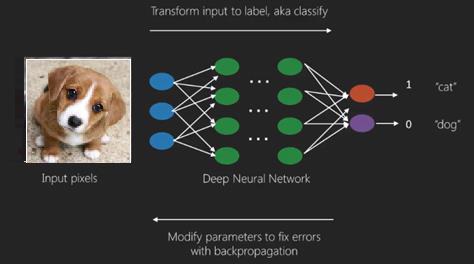
Ici, nous appliquons un algorithme de propagation arrière pour obtenir une prédiction de sortie correcte.

L'ensemble de données le plus élémentaire de l'apprentissage en profondeur est le MNIST, un ensemble de données de chiffres manuscrits.

Nous pouvons entraîner en profondeur un réseau neuronal convolutif avec Keras pour classer les images de chiffres manuscrits de cet ensemble de données.

Le déclenchement ou l'activation d'un classificateur de réseau neuronal produit un score. Par exemple, pour classer les patients comme malades et en bonne santé, nous considérons des paramètres tels que la taille, le poids et la température corporelle, la pression artérielle, etc.

Un score élevé signifie que le patient est malade et un score faible signifie qu'il est en bonne santé.

Chaque nœud des couches de sortie et masquées a ses propres classificateurs. La couche d'entrée prend des entrées et transmet ses scores à la couche cachée suivante pour une activation supplémentaire et cela continue jusqu'à ce que la sortie soit atteinte.

Cette progression de l'entrée à la sortie de gauche à droite dans le sens avant est appelée forward propagation.

Le chemin d'assignation de crédit (CAP) dans un réseau de neurones est la série de transformations commençant de l'entrée à la sortie. Les CAP élaborent des connexions causales probables entre l'entrée et la sortie.

La profondeur CAP pour un réseau neuronal à anticipation donné ou la profondeur CAP est le nombre de couches cachées plus une lorsque la couche de sortie est incluse. Pour les réseaux de neurones récurrents, où un signal peut se propager à travers une couche plusieurs fois, la profondeur CAP peut être potentiellement illimitée.

Filets profonds et filets peu profonds

Il n'y a pas de seuil clair de profondeur qui sépare l'apprentissage superficiel de l'apprentissage profond; mais il est généralement admis que pour l'apprentissage en profondeur qui a plusieurs couches non linéaires, le CAP doit être supérieur à deux.

Le nœud de base dans un réseau neuronal est une perception imitant un neurone dans un réseau neuronal biologique. Ensuite, nous avons la perception multicouche ou MLP. Chaque ensemble d'entrées est modifié par un ensemble de pondérations et de biais; chaque arête a un poids unique et chaque nœud a un biais unique.

La prédiction accuracy d'un réseau neuronal dépend de son weights and biases.

Le processus d'amélioration de la précision du réseau neuronal s'appelle training. La sortie d'un réseau prop avant est comparée à cette valeur qui est connue pour être correcte.

le cost function or the loss function est la différence entre la sortie générée et la sortie réelle.

Le but de la formation est de réduire au maximum le coût de la formation sur des millions d'exemples de formation. Pour ce faire, le réseau ajuste les poids et les biais jusqu'à ce que la prédiction corresponde au résultat correct.

Une fois bien formé, un réseau neuronal a le potentiel de faire une prédiction précise à chaque fois.

Lorsque le modèle devient complexe et que vous voulez que votre ordinateur les reconnaisse, vous devez opter pour des réseaux de neurones. Dans ces scénarios de modèle complexes, le réseau de neurones surpasse tous les autres algorithmes concurrents.

Il existe maintenant des GPU qui peuvent les entraîner plus rapidement que jamais. Les réseaux de neurones profonds révolutionnent déjà le domaine de l'IA

Les ordinateurs se sont révélés efficaces pour effectuer des calculs répétitifs et suivre des instructions détaillées, mais n'ont pas été aussi bons pour reconnaître des modèles complexes.

S'il y a le problème de la reconnaissance de motifs simples, une machine à vecteurs de support (svm) ou un classificateur de régression logistique peut bien faire le travail, mais à mesure que la complexité des motifs augmente, il n'y a pas d'autre moyen que d'opter pour des réseaux de neurones profonds.

Par conséquent, pour des modèles complexes comme un visage humain, les réseaux de neurones peu profonds échouent et n'ont pas d'autre alternative que d'opter pour des réseaux de neurones profonds avec plus de couches. Les filets profonds sont capables de faire leur travail en décomposant les modèles complexes en modèles plus simples. Par exemple, visage humain; adeep net utiliserait des bords pour détecter des parties comme les lèvres, le nez, les yeux, les oreilles, etc., puis les combinerait à nouveau pour former un visage humain

La précision de la prédiction correcte est devenue si précise que récemment, lors d'un défi de reconnaissance de modèle Google, un filet profond a battu un humain.

Cette idée d'un réseau de perceptrons en couches existe depuis un certain temps; dans ce domaine, des filets profonds imitent le cerveau humain. Mais un inconvénient est qu'ils prennent beaucoup de temps à s'entraîner, une contrainte matérielle

Cependant, les GPU hautes performances récents ont pu entraîner de tels réseaux profonds en moins d'une semaine; tandis que les cpus rapides auraient pu prendre des semaines voire des mois pour faire de même.

Choisir un Deep Net

Comment choisir un deep net? Nous devons décider si nous construisons un classificateur ou si nous essayons de trouver des modèles dans les données et si nous allons utiliser l'apprentissage non supervisé. Pour extraire des modèles d'un ensemble de données non étiquetées, nous utilisons une machine Boltzman restreinte ou un encodeur automatique.

Tenez compte des points suivants lors du choix d'un filet profond -

Pour le traitement de texte, l'analyse des sentiments, l'analyse syntaxique et la reconnaissance d'entités de noms, nous utilisons un réseau de tenseur neuronal récurrent ou récursif ou RNTN;
Pour tout modèle de langage fonctionnant au niveau des caractères, nous utilisons le réseau récurrent.
Pour la reconnaissance d'image, nous utilisons le réseau de croyance profonde DBN ou réseau convolutif.
Pour la reconnaissance d'objets, nous utilisons un RNTN ou un réseau convolutif.
Pour la reconnaissance vocale, nous utilisons le net récurrent.

En général, les réseaux de croyances profondes et les perceptrons multicouches avec des unités linéaires rectifiées ou RELU sont tous deux de bons choix pour la classification.

Pour l'analyse des séries chronologiques, il est toujours recommandé d'utiliser le réseau récurrent.

Les réseaux neuronaux existent depuis plus de 50 ans; mais ce n'est que maintenant qu'ils ont pris de l'importance. La raison en est qu'ils sont difficiles à former; lorsque nous essayons de les entraîner avec une méthode appelée propagation arrière, nous nous heurtons à un problème appelé dégradés qui disparaissent ou explosent. Lorsque cela se produit, la formation prend plus de temps et la précision passe au second plan. Lors de la formation d'un ensemble de données, nous calculons constamment la fonction de coût, qui est la différence entre la sortie prévue et la sortie réelle d'un ensemble de données d'apprentissage étiquetées.La fonction de coût est ensuite minimisée en ajustant les poids et les valeurs de biais jusqu'à la valeur la plus basse. Est obtenu. Le processus de formation utilise un gradient, qui est la vitesse à laquelle le coût changera par rapport au changement des valeurs de poids ou de biais.

Réseaux Boltzman restreints ou auto-encodeurs - RBN

En 2006, une percée a été franchie dans la résolution du problème de la disparition des gradients. Geoff Hinton a conçu une nouvelle stratégie qui a conduit au développement deRestricted Boltzman Machine - RBM, un filet à deux couches peu profond.

La première couche est le visible couche et la deuxième couche est la hiddencouche. Chaque nœud de la couche visible est connecté à chaque nœud de la couche masquée. Le réseau est dit restreint car deux couches au sein de la même couche ne sont pas autorisées à partager une connexion.

Les auto-encodeurs sont des réseaux qui encodent les données d'entrée sous forme de vecteurs. Ils créent une représentation cachée ou compressée des données brutes. Les vecteurs sont utiles dans la réduction de dimensionnalité; le vecteur comprime les données brutes en un plus petit nombre de dimensions essentielles. Les auto-encodeurs sont associés à des décodeurs, ce qui permet la reconstruction des données d'entrée en fonction de leur représentation cachée.

RBM est l'équivalent mathématique d'un traducteur bidirectionnel. Une passe avant prend les entrées et les traduit en un ensemble de nombres qui encode les entrées. Un passage en arrière prend quant à lui cet ensemble de nombres et les traduit à nouveau en entrées reconstruites. Un filet bien formé effectue un appui arrière avec un haut degré de précision.

Dans l'une ou l'autre des étapes, les pondérations et les biais ont un rôle critique; ils aident le RBM à décoder les interrelations entre les entrées et à décider quelles entrées sont essentielles pour détecter les modèles. Grâce à des passes avant et arrière, le RBM est formé pour reconstruire l'entrée avec différents poids et biais jusqu'à ce que l'entrée et la construction soient aussi proches que possible. Un aspect intéressant de la GAR est que les données n'ont pas besoin d'être étiquetées. Cela s'avère très important pour les ensembles de données du monde réel tels que les photos, les vidéos, les voix et les données de capteurs, qui ont tous tendance à ne pas être étiquetés. Au lieu d'étiqueter manuellement les données par des humains, RBM trie automatiquement les données; en ajustant correctement les poids et les biais, un RBM est capable d'extraire des caractéristiques importantes et de reconstruire les données d'entrée. RBM fait partie de la famille des réseaux neuronaux d'extraction de caractéristiques, conçus pour reconnaître les modèles inhérents aux données. Ces derniers sont également appelés auto-encodeurs car ils doivent encoder leur propre structure.

Réseaux de croyances profondes - DBN

Les réseaux de croyances profondes (DBN) sont formés en combinant les RBM et en introduisant une méthode de formation intelligente. Nous avons un nouveau modèle qui résout enfin le problème du gradient de fuite. Geoff Hinton a inventé les RBM et les Deep Belief Nets comme alternative à la propagation arrière.

Un DBN a une structure similaire à un MLP (Multi-layer perceptron), mais très différent en ce qui concerne la formation. c'est la formation qui permet aux DBN de surpasser leurs homologues peu profonds

Un DBN peut être visualisé comme une pile de RBM où la couche cachée d'un RBM est la couche visible du RBM au-dessus. Le premier RBM est formé pour reconstituer son entrée aussi précisément que possible.

La couche cachée du premier RBM est considérée comme la couche visible du second RBM et le second RBM est formé en utilisant les sorties du premier RBM. Ce processus est répété jusqu'à ce que chaque couche du réseau soit formée.

Dans un DBN, chaque RBM apprend toute l'entrée. Un DBN fonctionne globalement en affinant l'ensemble de l'entrée successivement à mesure que le modèle s'améliore lentement comme un objectif de caméra focalisant lentement une image. Une pile de RBM surpasse un seul RBM, car un MLP de perceptron multicouche surpasse un seul perceptron.

À ce stade, les RBM ont détecté des modèles inhérents aux données mais sans aucun nom ni étiquette. Pour terminer la formation du DBN, nous devons introduire des étiquettes dans les motifs et affiner le réseau avec un apprentissage supervisé.

Nous avons besoin d'un très petit ensemble d'échantillons étiquetés pour que les caractéristiques et les modèles puissent être associés à un nom. Ce petit ensemble de données est utilisé pour la formation. Cet ensemble de données étiquetées peut être très petit par rapport à l'ensemble de données d'origine.

Les poids et les biais sont légèrement modifiés, ce qui entraîne un léger changement dans la perception des motifs par le filet et souvent une petite augmentation de la précision totale.

La formation peut également être complétée dans un laps de temps raisonnable en utilisant des GPU donnant des résultats très précis par rapport aux réseaux peu profonds et nous voyons également une solution au problème de gradient de disparition.

Réseaux d'adversaires génératifs - GAN

Les réseaux antagonistes génératifs sont des réseaux neuronaux profonds comprenant deux réseaux, opposés l'un contre l'autre, d'où le nom «antagoniste».

Les GAN ont été introduits dans un article publié par des chercheurs de l'Université de Montréal en 2014. L'expert en IA de Facebook, Yann LeCun, se référant aux GAN, a qualifié la formation contradictoire de «l'idée la plus intéressante des 10 dernières années en ML».

Le potentiel des GAN est énorme, car l'analyse du réseau apprend à imiter toute distribution de données. Les GAN peuvent apprendre à créer des mondes parallèles étonnamment similaires au nôtre dans n'importe quel domaine: images, musique, discours, prose. Ce sont en quelque sorte des artistes robots et leur production est assez impressionnante.

Dans un GAN, un réseau neuronal, connu sous le nom de générateur, génère de nouvelles instances de données, tandis que l'autre, le discriminateur, évalue leur authenticité.

Disons que nous essayons de générer des chiffres écrits à la main comme ceux trouvés dans le jeu de données MNIST, qui est tiré du monde réel. Le travail du discriminateur, lorsqu'on lui montre une instance du véritable jeu de données MNIST, est de les reconnaître comme authentiques.

Considérons maintenant les étapes suivantes du GAN -

Le réseau de générateurs prend une entrée sous forme de nombres aléatoires et renvoie une image.
Cette image générée est donnée en entrée au réseau discriminateur avec un flux d'images prises à partir du jeu de données réel.
Le discriminateur prend à la fois des images réelles et fausses et renvoie des probabilités, un nombre compris entre 0 et 1, 1 représentant une prédiction d'authenticité et 0 représentant une fausse.
Vous avez donc une double boucle de rétroaction -
- Le discriminateur est dans une boucle de rétroaction avec la vérité terrain des images, que nous connaissons.
- Le générateur est dans une boucle de rétroaction avec le discriminateur.

Réseaux de neurones récurrents - RNN

RNNSare des réseaux de neurones dans lesquels les données peuvent circuler dans n'importe quelle direction. Ces réseaux sont utilisés pour des applications telles que la modélisation du langage ou le traitement du langage naturel (NLP).

Le concept de base sous-jacent aux RNN est d'utiliser des informations séquentielles. Dans un réseau neuronal normal, on suppose que toutes les entrées et sorties sont indépendantes les unes des autres. Si nous voulons prédire le mot suivant dans une phrase, nous devons savoir quels mots l'ont précédé.

Les RNN sont appelés récurrents car ils répètent la même tâche pour chaque élément d'une séquence, la sortie étant basée sur les calculs précédents. On peut donc dire que les RNN ont une «mémoire» qui capture des informations sur ce qui a été précédemment calculé. En théorie, les RNN peuvent utiliser des informations dans de très longues séquences, mais en réalité, ils ne peuvent regarder en arrière que quelques étapes.

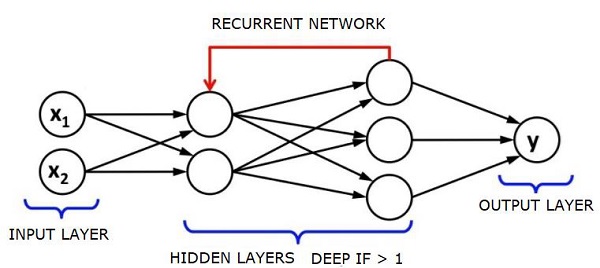
Les réseaux de mémoire à long terme (LSTM) sont les RNN les plus couramment utilisés.

Avec les réseaux de neurones convolutifs, les RNN ont été utilisés dans le cadre d'un modèle pour générer des descriptions d'images non étiquetées. Il est assez étonnant de voir à quel point cela semble fonctionner.

Réseaux de neurones profonds convolutifs - CNN

Si nous augmentons le nombre de couches dans un réseau de neurones pour le rendre plus profond, cela augmente la complexité du réseau et nous permet de modéliser des fonctions plus compliquées. Cependant, le nombre de pondérations et de biais augmentera de façon exponentielle. En fait, l'apprentissage de problèmes aussi difficiles peut devenir impossible pour les réseaux de neurones normaux. Cela conduit à une solution, les réseaux de neurones convolutifs.

Les CNN sont largement utilisés dans la vision par ordinateur; ont également été appliqués à la modélisation acoustique pour la reconnaissance automatique de la parole.

L'idée derrière les réseaux de neurones convolutifs est l'idée d'un «filtre mobile» qui traverse l'image. Ce filtre mobile, ou convolution, s'applique à un certain voisinage de nœuds qui peuvent par exemple être des pixels, où le filtre appliqué est 0,5 x la valeur du nœud -

Le chercheur renommé Yann LeCun a été le pionnier des réseaux de neurones convolutifs. Facebook en tant que logiciel de reconnaissance faciale utilise ces filets. CNN a été la solution idéale pour les projets de vision industrielle. Il existe de nombreuses couches dans un réseau convolutif. Dans le défi Imagenet, une machine a pu battre un humain lors de la reconnaissance d'objets en 2015.

En un mot, les réseaux de neurones convolutionnels (CNN) sont des réseaux de neurones multicouches. Les couches sont parfois jusqu'à 17 ou plus et supposent que les données d'entrée sont des images.

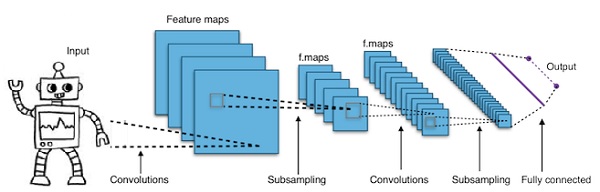
Les CNN réduisent considérablement le nombre de paramètres à régler. Ainsi, les CNN gèrent efficacement la haute dimensionnalité des images brutes.

Dans ce chapitre, nous examinerons les principes de base de Python Deep Learning.

Modèles / algorithmes d'apprentissage profond

Découvrons maintenant les différents modèles / algorithmes d'apprentissage profond.

Certains des modèles populaires dans l'apprentissage en profondeur sont les suivants:

Réseaux de neurones convolutifs
Réseaux de neurones récurrents
Réseaux de croyances profondes
Réseaux antagonistes génératifs
Auto-encodeurs et ainsi de suite

Les entrées et sorties sont représentées sous forme de vecteurs ou de tenseurs. Par exemple, un réseau neuronal peut avoir les entrées où les valeurs RVB des pixels individuels dans une image sont représentées sous forme de vecteurs.

Les couches de neurones qui se trouvent entre la couche d'entrée et la couche de sortie sont appelées couches cachées. C'est là que se déroule l'essentiel du travail lorsque le réseau neuronal tente de résoudre des problèmes. Un examen plus approfondi des couches cachées peut en révéler beaucoup sur les fonctionnalités que le réseau a appris à extraire des données.

Différentes architectures de réseaux de neurones sont formées en choisissant les neurones à connecter aux autres neurones de la couche suivante.

Pseudocode pour le calcul de la sortie

Voici le pseudo-code pour calculer la sortie de Forward-propagating Neural Network -

# node []: = tableau de nœuds triés topologiquement
# Une arête de a à b signifie que a est à gauche de b
# Si le réseau neuronal a des entrées R et des sorties S,
# alors les premiers nœuds R sont des nœuds d'entrée et les derniers nœuds S sont des nœuds de sortie.
# entrant [x]: = nœuds connectés au nœud x
# weight [x]: = poids des arêtes entrantes vers x

Pour chaque neurone x, de gauche à droite -

si x <= R: ne rien faire # c'est un nœud d'entrée
entrées [x] = [sortie [i] pour i en entrée [x]]
weighted_sum = dot_product (poids [x], entrées [x])
sortie [x] = fonction_activation (somme_poids)

Nous allons maintenant apprendre à former un réseau de neurones. Nous allons également apprendre l'algorithme de propagation en arrière et le passage en arrière dans Python Deep Learning.

Nous devons trouver les valeurs optimales des poids d'un réseau de neurones pour obtenir la sortie souhaitée. Pour entraîner un réseau de neurones, nous utilisons la méthode itérative de descente de gradient. Nous commençons d'abord par une initialisation aléatoire des poids. Après l'initialisation aléatoire, nous faisons des prédictions sur un sous-ensemble des données avec un processus de propagation avant, calculons la fonction de coût C correspondante et mettons à jour chaque poids w d'un montant proportionnel à dC / dw, c'est-à-dire la dérivée des fonctions de coût par rapport au poids. La constante de proportionnalité est connue sous le nom de taux d'apprentissage.

Les gradients peuvent être calculés efficacement en utilisant l'algorithme de rétro-propagation. L'observation clé de la propagation vers l'arrière ou de l'hélice arrière est qu'en raison de la règle de la chaîne de différenciation, le gradient au niveau de chaque neurone du réseau neuronal peut être calculé en utilisant le gradient au niveau des neurones, il a des bords sortants vers. Par conséquent, nous calculons les gradients à l'envers, c'est-à-dire que nous calculons d'abord les gradients de la couche de sortie, puis la couche cachée la plus haute, suivie de la couche cachée précédente, et ainsi de suite, se terminant à la couche d'entrée.

L'algorithme de rétro-propagation est implémenté principalement en utilisant l'idée d'un graphe de calcul, où chaque neurone est étendu à de nombreux nœuds dans le graphe de calcul et effectue une opération mathématique simple comme l'addition, la multiplication. Le graphe de calcul n'a pas de poids sur les arêtes; tous les poids sont attribués aux nœuds, de sorte que les poids deviennent leurs propres nœuds. L'algorithme de propagation vers l'arrière est ensuite exécuté sur le graphe de calcul. Une fois le calcul terminé, seuls les gradients des nœuds de poids sont nécessaires pour la mise à jour. Le reste des dégradés peut être ignoré.

Technique d'optimisation de la descente de gradient

Une fonction d'optimisation couramment utilisée qui ajuste les poids en fonction de l'erreur qu'ils ont causée est appelée la «descente de gradient».

Le gradient est un autre nom pour la pente, et la pente, sur un graphique xy, représente la façon dont deux variables sont liées l'une à l'autre: la montée au cours de la course, le changement de distance au cours du changement de temps, etc. Dans ce cas, la pente est le rapport entre l'erreur du réseau et un poids unique; c'est-à-dire, comment l'erreur change-t-elle lorsque le poids varie.

Pour le dire plus précisément, nous voulons trouver quel poids produit le moins d'erreur. Nous voulons trouver le poids qui représente correctement les signaux contenus dans les données d'entrée, et les traduit en une classification correcte.

Au fur et à mesure qu'un réseau de neurones apprend, il ajuste lentement de nombreux poids afin qu'ils puissent mapper correctement le signal sur la signification. Le rapport entre l'erreur de réseau et chacun de ces poids est une dérivée, dE / dw, qui calcule la mesure dans laquelle une légère modification d'un poids entraîne une légère modification de l'erreur.

Chaque poids n'est qu'un facteur dans un réseau profond qui implique de nombreuses transformations; le signal du poids passe par des activations et des sommes sur plusieurs couches, nous utilisons donc la règle de calcul en chaîne pour remonter les activations et sorties du réseau, ce qui nous amène au poids en question et à sa relation avec l'erreur globale.

Étant donné que deux variables, l'erreur et le poids, sont médiées par une troisième variable, activation, à travers lequel le poids est passé. Nous pouvons calculer comment un changement de poids affecte un changement d'erreur en calculant d'abord comment un changement d'activation affecte un changement d'erreur, et comment un changement de poids affecte un changement d'activation.

L'idée de base de l'apprentissage profond n'est rien de plus que cela: ajuster les poids d'un modèle en réponse à l'erreur qu'il produit, jusqu'à ce que vous ne puissiez plus réduire l'erreur.

Le filet profond s'entraîne lentement si la valeur du gradient est petite et rapide si la valeur est élevée. Toute inexactitude dans la formation conduit à des résultats inexacts. Le processus de formation des réseaux de la sortie vers l'entrée est appelé propagation arrière ou arrière prop. Nous savons que la propagation vers l'avant commence par l'entrée et progresse vers l'avant. Back prop fait l'inverse / inverse en calculant le gradient de droite à gauche.

Chaque fois que nous calculons un dégradé, nous utilisons tous les dégradés précédents jusqu'à ce point.

Commençons par un nœud de la couche de sortie. Le bord utilise le dégradé à ce nœud. Au fur et à mesure que nous retournons dans les couches cachées, cela devient plus complexe. Le produit de deux nombres entre 0 et 1 vous donne un nombre plus petit. La valeur du gradient ne cesse de diminuer et, par conséquent, le support arrière prend beaucoup de temps à s'entraîner et la précision en souffre.

Défis des algorithmes d'apprentissage profond

Il existe certains défis à la fois pour les réseaux de neurones peu profonds et les réseaux de neurones profonds, comme le surajustement et le temps de calcul. Les DNN sont affectés par le surajustement en raison de l'utilisation de couches d'abstraction supplémentaires qui leur permettent de modéliser des dépendances rares dans les données d'apprentissage.

Regularizationdes méthodes telles que l'abandon, l'arrêt précoce, l'augmentation des données, l'apprentissage par transfert sont appliquées pendant l'entraînement pour lutter contre le surapprentissage. La régularisation d'abandon omet aléatoirement les unités des couches cachées pendant l'entraînement, ce qui permet d'éviter les dépendances rares. Les DNN prennent en compte plusieurs paramètres d'apprentissage tels que la taille, c'est-à-dire le nombre de couches et le nombre d'unités par couche, le taux d'apprentissage et les poids initiaux. La recherche de paramètres optimaux n'est pas toujours pratique en raison du coût élevé en temps et en ressources de calcul. Plusieurs hacks tels que le batching peuvent accélérer le calcul. La grande puissance de traitement des GPU a considérablement aidé le processus de formation, car les calculs matriciels et vectoriels nécessaires sont bien exécutés sur les GPU.

Abandonner

Le décrochage est une technique de régularisation populaire pour les réseaux de neurones. Les réseaux de neurones profonds sont particulièrement sujets au surajustement.

Voyons maintenant ce qu'est le décrochage et comment cela fonctionne.

Pour reprendre les mots de Geoffrey Hinton, l'un des pionniers du Deep Learning, «Si vous avez un réseau neuronal profond et qu'il n'est pas surajusté, vous devriez probablement en utiliser un plus grand et utiliser le décrochage».

Le décrochage est une technique où lors de chaque itération de descente de gradient, nous déposons un ensemble de nœuds sélectionnés aléatoirement. Cela signifie que nous ignorons certains nœuds au hasard comme s'ils n'existaient pas.

Chaque neurone est conservé avec une probabilité de q et chuté au hasard avec une probabilité 1-q. La valeur q peut être différente pour chaque couche du réseau neuronal. Une valeur de 0,5 pour les couches masquées et de 0 pour la couche d'entrée fonctionne bien sur un large éventail de tâches.

Lors de l'évaluation et de la prédiction, aucun abandon n'est utilisé. La sortie de chaque neurone est multipliée par q afin que l'entrée de la couche suivante ait la même valeur attendue.

L'idée derrière Dropout est la suivante - Dans un réseau de neurones sans régularisation du décrochage, les neurones développent une codépendance entre eux, ce qui conduit à un surajustement.

Astuce de mise en œuvre

Dropout est implémenté dans des bibliothèques telles que TensorFlow et Pytorch en gardant la sortie des neurones sélectionnés au hasard à 0. Autrement dit, bien que le neurone existe, sa sortie est écrasée en tant que 0.

Arrêt précoce

Nous entraînons les réseaux de neurones à l'aide d'un algorithme itératif appelé descente de gradient.

L'idée derrière l'arrêt précoce est intuitive; nous arrêtons la formation lorsque l'erreur commence à augmenter. Ici, par erreur, nous entendons l'erreur mesurée sur les données de validation, qui est la partie des données d'entraînement utilisées pour régler les hyper-paramètres. Dans ce cas, l'hyper-paramètre est le critère d'arrêt.

Augmentation des données

Processus par lequel nous augmentons le quantum de données dont nous disposons ou nous l'augmentons en utilisant des données existantes et en y appliquant des transformations. Les transformations exactes utilisées dépendent de la tâche que nous entendons accomplir. De plus, les transformations qui aident le réseau neuronal dépendent de son architecture.

Par exemple, dans de nombreuses tâches de vision par ordinateur telles que la classification d'objets, une technique efficace d'augmentation des données consiste à ajouter de nouveaux points de données qui sont des versions recadrées ou traduites des données originales.

Lorsqu'un ordinateur accepte une image comme entrée, il prend un tableau de valeurs de pixels. Disons que l'image entière est décalée vers la gauche de 15 pixels. Nous appliquons de nombreux décalages différents dans des directions différentes, ce qui entraîne un ensemble de données augmenté plusieurs fois la taille de l'ensemble de données d'origine.

Apprentissage par transfert

Le processus consistant à prendre un modèle pré-entraîné et à «affiner» le modèle avec notre propre jeu de données est appelé apprentissage par transfert. Il existe plusieurs façons de procéder, dont quelques-unes sont décrites ci-dessous -

Nous formons le modèle pré-entraîné sur un grand ensemble de données. Ensuite, nous supprimons la dernière couche du réseau et la remplaçons par une nouvelle couche avec des poids aléatoires.
Nous gèlons ensuite les poids de toutes les autres couches et formons le réseau normalement. Ici, le gel des couches ne change pas les poids pendant la descente du gradient ou l'optimisation.

Le concept sous-jacent est que le modèle pré-entraîné agira comme un extracteur de caractéristiques et que seule la dernière couche sera entraînée sur la tâche en cours.

La rétropropagation est implémentée dans des frameworks d'apprentissage profond tels que Tensorflow, Torch, Theano, etc., à l'aide de graphes de calcul. Plus important encore, la compréhension de la rétro-propagation sur les graphes de calcul combine plusieurs algorithmes différents et ses variations telles que le backprop à travers le temps et le backprop avec des poids partagés. Une fois que tout est converti en un graphe de calcul, ils sont toujours le même algorithme - il suffit de retourner la propagation sur les graphes de calcul.

Qu'est-ce que le graphe informatique

Un graphe de calcul est défini comme un graphe orienté où les nœuds correspondent à des opérations mathématiques. Les graphes informatiques sont un moyen d'exprimer et d'évaluer une expression mathématique.

Par exemple, voici une équation mathématique simple -

$$p = x+y$$

Nous pouvons dessiner un graphe de calcul de l'équation ci-dessus comme suit.

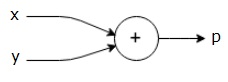
Le graphe de calcul ci-dessus a un nœud d'addition (nœud avec signe "+") avec deux variables d'entrée x et y et une sortie q.

Prenons un autre exemple, un peu plus complexe. Nous avons l'équation suivante.

$$g = \left (x+y \right ) \ast z $$

L'équation ci-dessus est représentée par le graphe de calcul suivant.

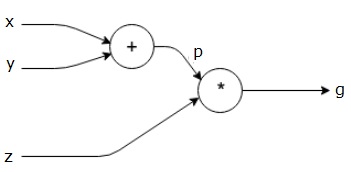
Graphiques informatiques et rétropropagation

Les graphes informatiques et la rétropropagation sont tous deux des concepts fondamentaux importants dans l'apprentissage en profondeur pour la formation des réseaux de neurones.

Passe avant

La passe avant est la procédure pour évaluer la valeur de l'expression mathématique représentée par des graphes de calcul. Faire une passe en avant signifie que nous transmettons la valeur des variables dans le sens avant de la gauche (entrée) à la droite où se trouve la sortie.

Prenons un exemple en donnant une certaine valeur à toutes les entrées. Supposons que les valeurs suivantes soient données à toutes les entrées.

$$x=1, y=3, z=−3$$

En donnant ces valeurs aux entrées, nous pouvons effectuer une passe avant et obtenir les valeurs suivantes pour les sorties sur chaque nœud.

Tout d'abord, nous utilisons la valeur de x = 1 et y = 3, pour obtenir p = 4.

Ensuite, nous utilisons p = 4 et z = -3 pour obtenir g = -12. Nous allons de gauche à droite, en avant.

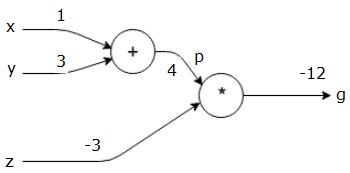
Objectifs de la passe arrière

Dans la passe en arrière, notre intention est de calculer les gradients pour chaque entrée par rapport à la sortie finale. Ces gradients sont essentiels pour entraîner le réseau neuronal à l'aide de la descente de gradient.

Par exemple, nous souhaitons les dégradés suivants.

Dégradés souhaités

$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$

Passage en arrière (rétropropagation)

Nous commençons la passe en arrière en trouvant la dérivée de la sortie finale par rapport à la sortie finale (elle-même!). Ainsi, il en résultera la dérivation d'identité et la valeur est égale à un.

$$\frac{\partial g}{\partial g} = 1$$

Notre graphe de calcul ressemble maintenant à celui ci-dessous -

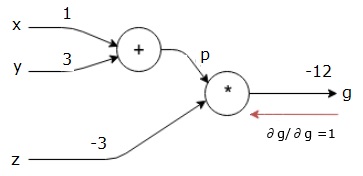
Ensuite, nous ferons le retour arrière par l'opération "*". Nous calculerons les gradients en p et z. Puisque g = p * z, nous savons que -

$$\frac{\partial g}{\partial z} = p$$

$$\frac{\partial g}{\partial p} = z$$

Nous connaissons déjà les valeurs de z et p de la passe avant. Par conséquent, nous obtenons -

$$\frac{\partial g}{\partial z} = p = 4$$

$$\frac{\partial g}{\partial p} = z = -3$$

Nous voulons calculer les gradients en x et y -

$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$

Cependant, nous voulons le faire efficacement (bien que x et g ne soient qu'à deux sauts dans ce graphique, imaginez qu'ils soient vraiment loin l'un de l'autre). Pour calculer efficacement ces valeurs, nous utiliserons la règle de la chaîne de différenciation. De la règle de la chaîne, nous avons -

$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$

$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$

Mais nous savons déjà que dg / dp = -3, dp / dx et dp / dy sont faciles puisque p dépend directement de x et y. Nous avons -

$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$

Par conséquent, nous obtenons -

$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \right ).1 = -3$$

De plus, pour l'entrée y -

$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$

La principale raison de faire cela à l'envers est que lorsque nous devions calculer le gradient en x, nous n'utilisions que des valeurs déjà calculées, et dq / dx (dérivée de la sortie du nœud par rapport à l'entrée du même nœud). Nous avons utilisé des informations locales pour calculer une valeur globale.

Étapes pour former un réseau de neurones

Suivez ces étapes pour former un réseau neuronal -

Pour le point de données x dans l'ensemble de données, nous transmettons en avant avec x en entrée et calculons le coût c en sortie.
Nous faisons des passes en arrière à partir de c et calculons les gradients pour tous les nœuds du graphique. Cela inclut les nœuds qui représentent les poids du réseau neuronal.
Nous mettons ensuite à jour les poids en faisant W = W - taux d'apprentissage * gradients.
Nous répétons ce processus jusqu'à ce que les critères d'arrêt soient satisfaits.

L'apprentissage en profondeur a produit de bons résultats pour quelques applications telles que la vision par ordinateur, la traduction linguistique, le sous-titrage d'images, la transcription audio, la biologie moléculaire, la reconnaissance vocale, le traitement du langage naturel, les voitures autonomes, la détection de tumeurs cérébrales, la traduction vocale en temps réel, la musique composition, jeu automatique et ainsi de suite.

L'apprentissage en profondeur est le prochain grand saut après l'apprentissage automatique avec une implémentation plus avancée. Actuellement, il est en passe de devenir une norme de l'industrie, apportant une forte promesse de changer la donne lorsqu'il s'agit de données brutes non structurées.

L'apprentissage en profondeur est actuellement l'un des meilleurs fournisseurs de solutions pour un large éventail de problèmes du monde réel. Les développeurs créent des programmes d'IA qui, au lieu d'utiliser des règles précédemment données, apprennent à partir d'exemples pour résoudre des tâches complexes. Avec l'apprentissage en profondeur utilisé par de nombreux scientifiques des données, les réseaux de neurones plus profonds fournissent des résultats toujours plus précis.

L'idée est de développer des réseaux de neurones profonds en augmentant le nombre de couches de formation pour chaque réseau; la machine en apprend plus sur les données jusqu'à ce qu'elles soient aussi précises que possible. Les développeurs peuvent utiliser des techniques d'apprentissage en profondeur pour mettre en œuvre des tâches d'apprentissage automatique complexes et former les réseaux d'IA pour obtenir des niveaux élevés de reconnaissance perceptive.

L'apprentissage profond trouve sa popularité dans la vision par ordinateur. Ici, l'une des tâches accomplies est la classification des images où les images d'entrée données sont classées en tant que chat, chien, etc. ou en tant que classe ou étiquette décrivant le mieux l'image. En tant qu'êtres humains, nous apprenons à accomplir cette tâche très tôt dans notre vie et avons ces compétences pour reconnaître rapidement des modèles, généraliser à partir de connaissances antérieures et s'adapter à différents environnements d'image.

Dans ce chapitre, nous allons relier l'apprentissage profond aux différentes bibliothèques et frameworks.

Apprentissage profond et Theano

Si nous voulons commencer à coder un réseau neuronal profond, il vaut mieux avoir une idée du fonctionnement de différents frameworks tels que Theano, TensorFlow, Keras, PyTorch, etc.

Theano est une bibliothèque python qui fournit un ensemble de fonctions pour créer des réseaux profonds qui s'entraînent rapidement sur notre machine.

Theano a été développé à l'Université de Montréal, Canada sous la direction de Yoshua Bengio, un pionnier du deep net.

Theano nous permet de définir et d'évaluer des expressions mathématiques avec des vecteurs et des matrices qui sont des tableaux rectangulaires de nombres.

Techniquement parlant, les réseaux neuronaux et les données d'entrée peuvent être représentés sous forme de matrices et toutes les opérations réseau standard peuvent être redéfinies en tant qu'opérations matricielles. Ceci est important car les ordinateurs peuvent effectuer des opérations matricielles très rapidement.

Nous pouvons traiter plusieurs valeurs de matrice en parallèle et si nous construisons un réseau neuronal avec cette structure sous-jacente, nous pouvons utiliser une seule machine avec un GPU pour former d'énormes réseaux dans une fenêtre de temps raisonnable.

Cependant, si nous utilisons Theano, nous devons construire le réseau profond à partir de zéro. La bibliothèque ne fournit pas de fonctionnalités complètes pour créer un type spécifique de réseau profond.

Au lieu de cela, nous devons coder tous les aspects du réseau profond comme le modèle, les couches, l'activation, la méthode d'entraînement et toutes les méthodes spéciales pour arrêter le surajustement.

La bonne nouvelle cependant est que Theano permet de construire notre implémentation sur un top de fonctions vectorisées nous offrant une solution hautement optimisée.

Il existe de nombreuses autres bibliothèques qui étendent les fonctionnalités de Theano. TensorFlow et Keras peuvent être utilisés avec Theano comme backend.

Apprentissage profond avec TensorFlow

Googles TensorFlow est une bibliothèque python. Cette bibliothèque est un excellent choix pour créer des applications d'apprentissage en profondeur de qualité commerciale.

TensorFlow est né d'une autre bibliothèque DistBelief V2 qui faisait partie de Google Brain Project. Cette bibliothèque vise à étendre la portabilité de l'apprentissage automatique afin que les modèles de recherche puissent être appliqués à des applications de niveau commercial.

Tout comme la bibliothèque Theano, TensorFlow est basé sur des graphes de calcul où un nœud représente des données persistantes ou une opération mathématique et les arêtes représentent le flux de données entre les nœuds, qui est un tableau ou un tenseur multidimensionnel; d'où le nom TensorFlow

La sortie d'une opération ou d'un ensemble d'opérations est introduite comme entrée dans la suivante.

Même si TensorFlow a été conçu pour les réseaux de neurones, il fonctionne bien pour d'autres réseaux où le calcul peut être modélisé sous forme de graphique de flux de données.

TensorFlow utilise également plusieurs fonctionnalités de Theano telles que l'élimination commune et sous-expression, la différenciation automatique, les variables partagées et symboliques.

Différents types de réseaux profonds peuvent être construits à l'aide de TensorFlow, tels que les réseaux convolutifs, les auto-encodeurs, RNTN, RNN, RBM, DBM / MLP, etc.

Cependant, il n'y a pas de prise en charge de la configuration des hyper-paramètres dans TensorFlow.Pour cette fonctionnalité, nous pouvons utiliser Keras.

Deep Learning et Keras

Keras est une puissante bibliothèque Python facile à utiliser pour développer et évaluer des modèles d'apprentissage en profondeur.

Il a un design minimaliste qui nous permet de construire un réseau couche par couche; entraînez-le et exécutez-le.

Il englobe les bibliothèques de calcul numérique efficaces Theano et TensorFlow et nous permet de définir et de former des modèles de réseaux neuronaux en quelques courtes lignes de code.

Il s'agit d'une API de réseau neuronal de haut niveau, aidant à utiliser largement l'apprentissage en profondeur et l'intelligence artificielle. Il s'exécute au-dessus d'un certain nombre de bibliothèques de niveau inférieur, notamment TensorFlow, Theano, etc. Le code Keras est portable; nous pouvons implémenter un réseau de neurones dans Keras en utilisant Theano ou TensorFlow comme back-end sans aucun changement de code.

Dans cette implémentation du Deep Learning, notre objectif est de prédire l'attrition des clients ou les données de barattage pour une certaine banque - quels clients sont susceptibles de quitter ce service bancaire. L'ensemble de données utilisé est relativement petit et contient 10 000 lignes avec 14 colonnes. Nous utilisons la distribution Anaconda et des frameworks comme Theano, TensorFlow et Keras. Keras est construit sur Tensorflow et Theano qui fonctionnent comme ses backends.

# Artificial Neural Network
# Installing Theano
pip install --upgrade theano

# Installing Tensorflow
pip install –upgrade tensorflow

# Installing Keras
pip install --upgrade keras

Étape 1: prétraitement des données

In[]:

# Importing the libraries
   import numpy as np
   import matplotlib.pyplot as plt
   import pandas as pd
 
# Importing the database
   dataset = pd.read_csv('Churn_Modelling.csv')

Étape 2

Nous créons des matrices des caractéristiques de l'ensemble de données et de la variable cible, qui est la colonne 14, étiquetée comme «Exited».

L'aspect initial des données est comme indiqué ci-dessous -

In[]:
X = dataset.iloc[:, 3:13].values
Y = dataset.iloc[:, 13].values
X

Production

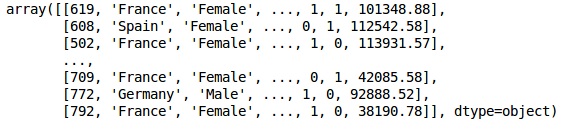
Étape 3

Production

array([1, 0, 1, ..., 1, 1, 0], dtype = int64)

Étape 4

Nous simplifions l'analyse en codant des variables de chaîne. Nous utilisons la fonction ScikitLearn 'LabelEncoder' pour encoder automatiquement les différentes étiquettes dans les colonnes avec des valeurs comprises entre 0 et n_classes-1.

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder_X_1 = LabelEncoder() 
X[:,1] = labelencoder_X_1.fit_transform(X[:,1]) 
labelencoder_X_2 = LabelEncoder() 
X[:, 2] = labelencoder_X_2.fit_transform(X[:, 2])
X

Production

Dans la sortie ci-dessus, les noms de pays sont remplacés par 0, 1 et 2; tandis que les hommes et les femmes sont remplacés par 0 et 1.

Étape 5

Labelling Encoded Data

Nous utilisons le même ScikitLearn bibliothèque et une autre fonction appelée OneHotEncoder pour simplement passer le numéro de colonne en créant une variable factice.

onehotencoder = OneHotEncoder(categorical features = [1])
X = onehotencoder.fit_transform(X).toarray()
X = X[:, 1:]
X

Désormais, les 2 premières colonnes représentent le pays et la 4ème colonne représente le sexe.

Production

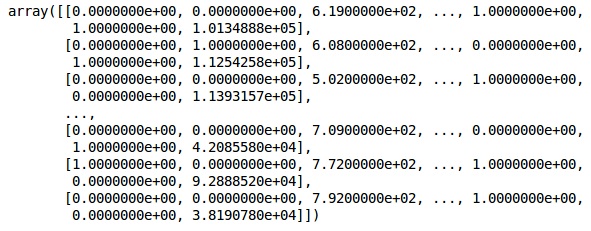
Nous divisons toujours nos données en partie formation et test; nous formons notre modèle sur les données de formation, puis nous vérifions l'exactitude d'un modèle sur les données de test, ce qui aide à évaluer l'efficacité du modèle.

Étape 6

Nous utilisons ScikitLearn train_test_splitfonction pour diviser nos données en ensemble d'entraînement et ensemble de test. Nous conservons le rapport de répartition train-test à 80:20.

#Splitting the dataset into the Training set and the Test Set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)

Certaines variables ont des valeurs en milliers tandis que d'autres ont des valeurs en dizaines ou en unités. Nous mettons les données à l'échelle pour qu'elles soient plus représentatives.

Étape 7

Dans ce code, nous ajustons et transformons les données d'entraînement à l'aide du StandardScalerfonction. Nous normalisons notre mise à l'échelle afin d'utiliser la même méthode ajustée pour transformer / mettre à l'échelle les données de test.

# Feature Scaling

fromsklearn.preprocessing import StandardScaler 
sc = StandardScaler() 
X_train = sc.fit_transform(X_train) 
X_test = sc.transform(X_test)

Production

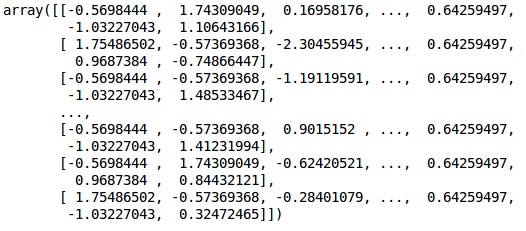
Les données sont désormais correctement mises à l'échelle. Enfin, nous en avons terminé avec notre prétraitement des données. Maintenant, nous allons commencer par notre modèle.

Étape 8

Nous importons ici les modules requis. Nous avons besoin du module Sequential pour initialiser le réseau neuronal et du module dense pour ajouter les couches cachées.

# Importing the Keras libraries and packages 
import keras 
from keras.models import Sequential 
from keras.layers import Dense

Étape 9

Nous nommerons le modèle comme classificateur car notre objectif est de classer le taux de désabonnement des clients. Ensuite, nous utilisons le module Sequential pour l'initialisation.

#Initializing Neural Network 
classifier = Sequential()

Étape 10

Nous ajoutons les couches cachées une par une en utilisant la fonction dense. Dans le code ci-dessous, nous verrons de nombreux arguments.

Notre premier paramètre est output_dim. C'est le nombre de nœuds que nous ajoutons à cette couche.initest l'initialisation du Stochastic Gradient Decent. Dans un réseau neuronal, nous attribuons des pondérations à chaque nœud. Lors de l'initialisation, les poids doivent être proches de zéro et nous initialisons aléatoirement les poids en utilisant la fonction uniforme. leinput_dimLe paramètre n'est nécessaire que pour la première couche, car le modèle ne connaît pas le nombre de nos variables d'entrée. Ici, le nombre total de variables d'entrée est de 11. Dans la deuxième couche, le modèle connaît automatiquement le nombre de variables d'entrée de la première couche cachée.

Exécutez la ligne de code suivante pour ajouter la couche d'entrée et la première couche cachée -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu', input_dim = 11))

Exécutez la ligne de code suivante pour ajouter le deuxième calque caché -

classifier.add(Dense(units = 6, kernel_initializer = 'uniform', 
activation = 'relu'))

Exécutez la ligne de code suivante pour ajouter la couche de sortie -

classifier.add(Dense(units = 1, kernel_initializer = 'uniform', 
activation = 'sigmoid'))

Étape 11

Compiling the ANN

Nous avons ajouté plusieurs couches à notre classificateur jusqu'à présent. Nous allons maintenant les compiler en utilisant lecompileméthode. Les arguments ajoutés dans le contrôle de compilation final complètent le réseau neuronal, nous devons donc être prudents dans cette étape.

Voici une brève explication des arguments.

Le premier argument est OptimizerIl s'agit d'un algorithme utilisé pour trouver l'ensemble optimal de poids. Cet algorithme s'appelle leStochastic Gradient Descent (SGD). Ici, nous utilisons un parmi plusieurs types, appelé «optimiseur Adam». Le SGD dépend de la perte, notre deuxième paramètre est donc la perte. Si notre variable dépendante est binaire, nous utilisons la fonction de perte logarithmique appelée‘binary_crossentropy’, et si notre variable dépendante a plus de deux catégories en sortie, alors nous utilisons ‘categorical_crossentropy’. Nous voulons améliorer les performances de notre réseau neuronal basé suraccuracy, alors on ajoute metrics comme précision.

# Compiling Neural Network 
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])

Étape 12

Un certain nombre de codes doivent être exécutés à cette étape.

Montage de l'ANN sur l'ensemble d'entraînement

Nous formons maintenant notre modèle sur les données d'entraînement. Nous utilisons lefitméthode adaptée à notre modèle. Nous optimisons également les pondérations pour améliorer l'efficacité du modèle. Pour cela, nous devons mettre à jour les poids.Batch size est le nombre d'observations après lequel nous mettons à jour les poids. Epochest le nombre total d'itérations. Les valeurs de taille de lot et d'époque sont choisies par la méthode d'essai et d'erreur.

classifier.fit(X_train, y_train, batch_size = 10, epochs = 50)

Faire des prédictions et évaluer le modèle

# Predicting the Test set results
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)

Prédire une seule nouvelle observation

# Predicting a single new observation
"""Our goal is to predict if the customer with the following data will leave the bank:
Geography: Spain
Credit Score: 500
Gender: Female
Age: 40
Tenure: 3
Balance: 50000
Number of Products: 2
Has Credit Card: Yes
Is Active Member: Yes

Étape 13

Predicting the test set result

Le résultat de la prédiction vous donnera la probabilité que le client quitte l'entreprise. Nous convertirons cette probabilité en 0 et 1 binaires.

# Predicting the Test set results 
y_pred = classifier.predict(X_test) 
y_pred = (y_pred > 0.5)

new_prediction = classifier.predict(sc.transform
(np.array([[0.0, 0, 500, 1, 40, 3, 50000, 2, 1, 1, 40000]])))
new_prediction = (new_prediction > 0.5)

Étape 14

C'est la dernière étape où nous évaluons les performances de notre modèle. Nous avons déjà des résultats originaux et nous pouvons donc construire une matrice de confusion pour vérifier l'exactitude de notre modèle.

Making the Confusion Matrix

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print (cm)

Production

loss: 0.3384 acc: 0.8605
[ [1541 54]
[230 175] ]

À partir de la matrice de confusion, la précision de notre modèle peut être calculée comme suit:

Accuracy = 1541+175/2000=0.858

We achieved 85.8% accuracy, ce qui est bon.

L'algorithme de propagation vers l'avant

Dans cette section, nous allons apprendre à écrire du code pour faire une propagation avant (prédiction) pour un simple réseau de neurones -

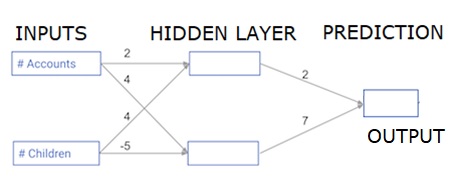
Chaque point de données est un client. La première entrée est le nombre de comptes qu'ils ont et la seconde le nombre d'enfants qu'ils ont. Le modèle prédira le nombre de transactions que l'utilisateur effectuera l'année prochaine.

Les données d'entrée sont préchargées en tant que données d'entrée et les poids sont dans un dictionnaire appelé poids. Le tableau de poids pour le premier nœud de la couche cachée est en poids ['node_0'], et pour le deuxième nœud dans la couche cachée sont en poids ['node_1'] respectivement.

Les poids alimentant le nœud de sortie sont disponibles en poids.

La fonction d'activation linéaire rectifiée

Une "fonction d'activation" est une fonction qui fonctionne à chaque nœud. Il transforme l'entrée du nœud en une sortie.

La fonction d'activation linéaire rectifiée (appelée ReLU ) est largement utilisée dans les réseaux à très hautes performances. Cette fonction prend un seul nombre comme entrée, renvoyant 0 si l'entrée est négative et entrée comme sortie si l'entrée est positive.

Voici quelques exemples -

relu (4) = 4
relu (-2) = 0

On remplit la définition de la fonction relu () -

Nous utilisons la fonction max () pour calculer la valeur de la sortie de relu ().
Nous appliquons la fonction relu () à node_0_input pour calculer node_0_output.
Nous appliquons la fonction relu () à node_1_input pour calculer node_1_output.

import numpy as np
input_data = np.array([-1, 2])
weights = {
   'node_0': np.array([3, 3]),
   'node_1': np.array([1, 5]),
   'output': np.array([2, -1])
}
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = np.tanh(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = np.tanh(node_1_input)
hidden_layer_output = np.array(node_0_output, node_1_output)
output =(hidden_layer_output * weights['output']).sum()
print(output)

def relu(input):
   '''Define your relu activation function here'''
   # Calculate the value for the output of the relu function: output
   output = max(input,0)
      # Return the value just calculated
   return(output)
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)

# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)

# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])

# Calculate model output (do not apply relu)
odel_output = (hidden_layer_outputs * weights['output']).sum()
print(model_output)# Print model output

Production

0.9950547536867305
-3

Application du réseau à de nombreuses observations / lignes de données

Dans cette section, nous allons apprendre à définir une fonction appelée predict_with_network (). Cette fonction générera des prédictions pour plusieurs observations de données, prises à partir du réseau ci-dessus pris comme input_data. Les poids donnés dans le réseau ci-dessus sont utilisés. La définition de la fonction relu () est également utilisée.

Définissons une fonction appelée predict_with_network () qui accepte deux arguments - input_data_row et weights - et renvoie une prédiction du réseau en sortie.

Nous calculons les valeurs d'entrée et de sortie pour chaque nœud, en les stockant sous la forme: node_0_input, node_0_output, node_1_input et node_1_output.

Pour calculer la valeur d'entrée d'un nœud, nous multiplions les tableaux pertinents ensemble et calculons leur somme.

Pour calculer la valeur de sortie d'un nœud, nous appliquons la fonction relu () à la valeur d'entrée du nœud. Nous utilisons une 'boucle for' pour itérer sur input_data -

Nous utilisons également notre predict_with_network () pour générer des prédictions pour chaque ligne de input_data - input_data_row. Nous ajoutons également chaque prédiction aux résultats.

# Define predict_with_network()
def predict_with_network(input_data_row, weights):
   # Calculate node 0 value
   node_0_input = (input_data_row * weights['node_0']).sum()
   node_0_output = relu(node_0_input)
   
   # Calculate node 1 value
   node_1_input = (input_data_row * weights['node_1']).sum()
   node_1_output = relu(node_1_input)
   
   # Put node values into array: hidden_layer_outputs
   hidden_layer_outputs = np.array([node_0_output, node_1_output])
   
   # Calculate model output
   input_to_final_layer = (hidden_layer_outputs*weights['output']).sum()
   model_output = relu(input_to_final_layer)
# Return model output
   return(model_output)

# Create empty list to store prediction results
results = []
for input_data_row in input_data:
   # Append prediction to results
   results.append(predict_with_network(input_data_row, weights))
print(results)# Print results

Production

[0, 12]

Ici, nous avons utilisé la fonction relu où relu (26) = 26 et relu (-13) = 0 et ainsi de suite.

Réseaux de neurones multicouches profonds

Ici, nous écrivons du code pour faire la propagation avant pour un réseau de neurones avec deux couches cachées. Chaque couche cachée a deux nœuds. Les données d'entrée ont été préchargées commeinput_data. Les nœuds de la première couche masquée sont appelés node_0_0 et node_0_1.

Leurs poids sont préchargés sous forme de poids ['node_0_0'] et de poids ['node_0_1'] respectivement.

Les nœuds de la deuxième couche cachée sont appelés node_1_0 and node_1_1. Leurs poids sont préchargés commeweights['node_1_0'] et weights['node_1_1'] respectivement.

Nous créons ensuite une sortie de modèle à partir des nœuds cachés en utilisant des poids préchargés comme weights['output'].

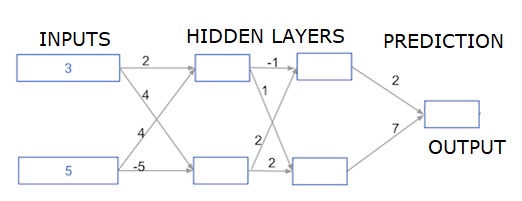
Nous calculons node_0_0_input en utilisant ses poids pondérés ['node_0_0'] et les données d'entrée données. Appliquez ensuite la fonction relu () pour obtenir node_0_0_output.

Nous faisons la même chose que ci-dessus pour node_0_1_input afin d'obtenir node_0_1_output.

Nous calculons node_1_0_input en utilisant ses poids pondérés ['node_1_0'] et les sorties de la première couche cachée - hidden_0_outputs. Nous appliquons ensuite la fonction relu () pour obtenir node_1_0_output.

Nous faisons la même chose que ci-dessus pour node_1_1_input afin d'obtenir node_1_1_output.

Nous calculons model_output en utilisant les poids ['output'] et les sorties du deuxième tableau hidden_1_outputs de la couche cachée. Nous n'appliquons pas la fonction relu () à cette sortie.

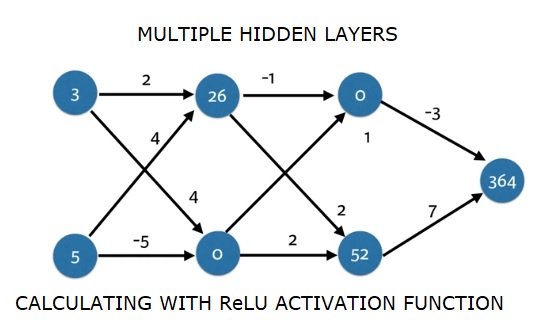
import numpy as np
input_data = np.array([3, 5])
weights = {
   'node_0_0': np.array([2, 4]),
   'node_0_1': np.array([4, -5]),
   'node_1_0': np.array([-1, 1]),
   'node_1_1': np.array([2, 2]),
   'output': np.array([2, 7])
}
def predict_with_network(input_data):
   # Calculate node 0 in the first hidden layer
   node_0_0_input = (input_data * weights['node_0_0']).sum()
   node_0_0_output = relu(node_0_0_input)
   
   # Calculate node 1 in the first hidden layer
   node_0_1_input = (input_data*weights['node_0_1']).sum()
   node_0_1_output = relu(node_0_1_input)
   
   # Put node values into array: hidden_0_outputs
   hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
   
   # Calculate node 0 in the second hidden layer
   node_1_0_input = (hidden_0_outputs*weights['node_1_0']).sum()
   node_1_0_output = relu(node_1_0_input)
   
   # Calculate node 1 in the second hidden layer
   node_1_1_input = (hidden_0_outputs*weights['node_1_1']).sum()
   node_1_1_output = relu(node_1_1_input)
   
   # Put node values into array: hidden_1_outputs
   hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
   
   # Calculate model output: model_output
   model_output = (hidden_1_outputs*weights['output']).sum()
      # Return model_output
   return(model_output)
output = predict_with_network(input_data)
print(output)

Production