PyTorch - Régression linéaire

Dans ce chapitre, nous nous concentrerons sur un exemple de base d'implémentation de régression linéaire à l'aide de TensorFlow. La régression logistique ou régression linéaire est une approche d'apprentissage automatique supervisé pour la classification des catégories discrètes d'ordre. Notre objectif dans ce chapitre est de construire un modèle par lequel un utilisateur peut prédire la relation entre les variables prédictives et une ou plusieurs variables indépendantes.

La relation entre ces deux variables est considérée comme linéaire, c'est-à-dire que si y est la variable dépendante et x est considéré comme la variable indépendante, alors la relation de régression linéaire de deux variables ressemblera à l'équation mentionnée ci-dessous -

Y = Ax+b

Ensuite, nous allons concevoir un algorithme de régression linéaire qui nous permet de comprendre deux concepts importants donnés ci-dessous -

Fonction de coût
Algorithmes de descente de gradient

La représentation schématique de la régression linéaire est mentionnée ci-dessous

Interpréter le résultat

$$ Y = ax + b $$

La valeur de a est la pente.
La valeur de b est le y − intercept.
r est le correlation coefficient.
r² est le correlation coefficient.

La vue graphique de l'équation de régression linéaire est mentionnée ci-dessous -

Les étapes suivantes sont utilisées pour implémenter la régression linéaire à l'aide de PyTorch -

Étape 1

Importez les packages nécessaires pour créer une régression linéaire dans PyTorch en utilisant le code ci-dessous -

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline

sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = True

Étape 2

Créez un seul ensemble d'entraînement avec l'ensemble de données disponible, comme indiqué ci-dessous -

m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = x * m + c + noise

df = pd.DataFrame()
df['x'] = x
df['y'] = y

sns.lmplot(x ='x', y ='y', data = df)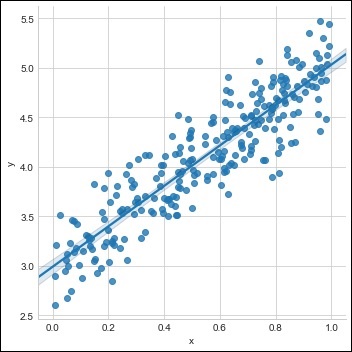

Étape 3

Implémentez la régression linéaire avec les bibliothèques PyTorch comme mentionné ci-dessous -

import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

class LinearRegressionModel(nn.Module):
   def __init__(self, input_dim, output_dim):
      super(LinearRegressionModel, self).__init__()
      self.linear = nn.Linear(input_dim, output_dim)

   def forward(self, x):
      out = self.linear(x)
      return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()

def get_param_values():
   return w.data[0][0], b.data[0]

def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')

Le tracé généré est le suivant -