PyTorch - Guide rapide
PyTorch est défini comme une bibliothèque d'apprentissage automatique open source pour Python. Il est utilisé pour des applications telles que le traitement du langage naturel. Il est initialement développé par le groupe de recherche sur l'intelligence artificielle de Facebook et le logiciel Pyro d'Uber pour la programmation probabiliste qui en est basé.
À l'origine, PyTorch a été développé par Hugh Perkins en tant que wrapper Python pour LusJIT basé sur le framework Torch. Il existe deux variantes de PyTorch.
PyTorch repense et implémente Torch en Python tout en partageant les mêmes bibliothèques C de base pour le code backend. Les développeurs PyTorch ont réglé ce code back-end pour exécuter Python efficacement. Ils ont également conservé l'accélération matérielle basée sur le GPU ainsi que les fonctionnalités d'extensibilité qui ont fait Torch basé sur Lua.
traits
Les principales caractéristiques de PyTorch sont mentionnées ci-dessous -
Easy Interface- PyTorch offre une API facile à utiliser; par conséquent, il est considéré comme très simple à utiliser et fonctionne sur Python. L'exécution du code dans ce cadre est assez simple.
Python usage- Cette bibliothèque est considérée comme Pythonic et s'intègre parfaitement à la pile de science des données Python. Ainsi, il peut tirer parti de tous les services et fonctionnalités offerts par l'environnement Python.
Computational graphs- PyTorch fournit une excellente plate-forme qui offre des graphiques de calcul dynamiques. Ainsi, un utilisateur peut les modifier pendant l'exécution. Ceci est très utile lorsqu'un développeur n'a aucune idée de la quantité de mémoire requise pour créer un modèle de réseau neuronal.
PyTorch est connu pour avoir trois niveaux d'abstraction comme indiqué ci-dessous -
Tensor - Tableau n-dimensionnel impératif qui fonctionne sur GPU.
Variable - Nœud dans le graphe de calcul. Cela stocke les données et le gradient.
Module - Couche de réseau neuronal qui stockera l'état ou les poids apprenables.
Avantages de PyTorch
Voici les avantages de PyTorch -
Il est facile de déboguer et de comprendre le code.
Il comprend de nombreuses couches comme Torch.
Il comprend de nombreuses fonctions de perte.
Il peut être considéré comme une extension NumPy des GPU.
Il permet de construire des réseaux dont la structure dépend du calcul lui-même.
TensorFlow contre PyTorch
Nous examinerons ci-dessous les principales différences entre TensorFlow et PyTorch -
| PyTorch | TensorFlow |
|---|---|
PyTorch est étroitement lié au framework Torch basé sur lua qui est activement utilisé dans Facebook. |
TensorFlow est développé par Google Brain et activement utilisé chez Google. |
PyTorch est relativement nouveau par rapport aux autres technologies concurrentes. |
TensorFlow n'est pas nouveau et est considéré comme un outil incontournable par de nombreux chercheurs et professionnels de l'industrie. |
PyTorch inclut tout de manière impérative et dynamique. |
TensorFlow comprend des graphiques statiques et dynamiques sous forme de combinaison. |
Le graphe de calcul dans PyTorch est défini pendant l'exécution. |
TensorFlow n'inclut aucune option d'exécution. |
PyTorch inclut le déploiement pour les frameworks mobiles et embarqués. |
TensorFlow fonctionne mieux pour les frameworks intégrés. |
PyTorch est un framework d'apprentissage en profondeur populaire. Dans ce tutoriel, nous considérons «Windows 10» comme notre système d'exploitation. Les étapes pour une configuration environnementale réussie sont les suivantes -
Étape 1
Le lien suivant comprend une liste de packages qui comprend des packages appropriés pour PyTorch.
https://drive.google.com/drive/folders/0B-X0-FlSGfCYdTNldW02UGl4MXMTout ce que vous avez à faire est de télécharger les packages respectifs et de l'installer comme indiqué dans les captures d'écran suivantes -


Étape 2
Cela implique de vérifier l'installation du framework PyTorch à l'aide d'Anaconda Framework.
La commande suivante est utilisée pour vérifier la même chose -
conda list
«Conda list» affiche la liste des frameworks installés.

La partie en surbrillance montre que PyTorch a été installé avec succès dans notre système.
Les mathématiques sont vitales dans tout algorithme d'apprentissage automatique et incluent divers concepts de base des mathématiques pour obtenir le bon algorithme conçu d'une manière spécifique.
L'importance des sujets mathématiques pour l'apprentissage automatique et la science des données est mentionnée ci-dessous -

Maintenant, concentrons-nous sur les principaux concepts mathématiques de l'apprentissage automatique qui sont importants du point de vue du traitement du langage naturel -
Vecteurs
Le vecteur est considéré comme un tableau de nombres qui est soit continu soit discret et l'espace qui se compose de vecteurs est appelé espace vectoriel. Les dimensions spatiales des vecteurs peuvent être finies ou infinies, mais il a été observé que les problèmes d'apprentissage automatique et de science des données traitent de vecteurs de longueur fixe.
La représentation vectorielle est affichée comme indiqué ci-dessous -
temp = torch.FloatTensor([23,24,24.5,26,27.2,23.0])
temp.size()
Output - torch.Size([6])Dans l'apprentissage automatique, nous traitons des données multidimensionnelles. Les vecteurs deviennent donc très cruciaux et sont considérés comme des caractéristiques d'entrée pour tout énoncé de problème de prédiction.
Scalaires
Les scalaires sont appelés à avoir des dimensions nulles contenant une seule valeur. Quand il s'agit de PyTorch, il n'inclut pas de tenseur spécial avec des dimensions nulles; par conséquent, la déclaration sera faite comme suit -
x = torch.rand(10)
x.size()
Output - torch.Size([10])Matrices
La plupart des données structurées sont généralement représentées sous forme de tableaux ou d'une matrice spécifique. Nous utiliserons un ensemble de données appelé Boston House Prices, qui est facilement disponible dans la bibliothèque d'apprentissage automatique de Python scikit-learn.
boston_tensor = torch.from_numpy(boston.data)
boston_tensor.size()
Output: torch.Size([506, 13])
boston_tensor[:2]
Output:
Columns 0 to 7
0.0063 18.0000 2.3100 0.0000 0.5380 6.5750 65.2000 4.0900
0.0273 0.0000 7.0700 0.0000 0.4690 6.4210 78.9000 4.9671
Columns 8 to 12
1.0000 296.0000 15.3000 396.9000 4.9800
2.0000 242.0000 17.8000 396.9000 9.1400Le principe principal du réseau neuronal comprend une collection d'éléments de base, c'est-à-dire un neurone artificiel ou un perceptron. Il comprend plusieurs entrées de base telles que x1, x2… .. xn qui produit une sortie binaire si la somme est supérieure au potentiel d'activation.
La représentation schématique de l'échantillon de neurone est mentionnée ci-dessous -

La sortie générée peut être considérée comme la somme pondérée avec potentiel d'activation ou biais.
$$ Sortie = \ sum_jw_jx_j + Biais $$
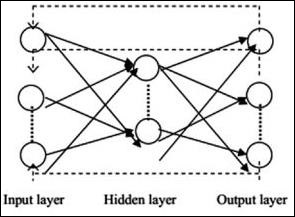
L'architecture de réseau neuronal typique est décrite ci-dessous -

Les couches entre l'entrée et la sortie sont appelées couches cachées, et la densité et le type de connexions entre les couches est la configuration. Par exemple, une configuration entièrement connectée a tous les neurones de la couche L connectés à ceux de L + 1. Pour une localisation plus prononcée, nous ne pouvons connecter qu'un voisinage local, disons neuf neurones, à la couche suivante. La figure 1-9 illustre deux couches cachées avec des connexions denses.
Les différents types de réseaux de neurones sont les suivants -
Réseaux de neurones feedforward
Les réseaux de neurones à feedforward comprennent des unités de base de la famille des réseaux de neurones. Le mouvement des données dans ce type de réseau neuronal se fait de la couche d'entrée à la couche de sortie, via les couches cachées présentes. La sortie d'une couche sert de couche d'entrée avec des restrictions sur tout type de boucles dans l'architecture du réseau.

Réseaux de neurones récurrents
Les réseaux de neurones récurrents se produisent lorsque le modèle de données change en conséquence sur une période. Dans RNN, la même couche est appliquée pour accepter les paramètres d'entrée et afficher les paramètres de sortie dans le réseau neuronal spécifié.
Les réseaux neuronaux peuvent être construits à l'aide du package torch.nn.

Il s'agit d'un simple réseau à réaction. Il prend l'entrée, l'alimente à travers plusieurs couches l'une après l'autre, puis donne finalement la sortie.
Avec l'aide de PyTorch, nous pouvons utiliser les étapes suivantes pour une procédure d'entraînement typique pour un réseau de neurones -
- Définissez le réseau neuronal qui a des paramètres (ou pondérations) apprenables.
- Itérer sur un ensemble de données d'entrées.
- Traitez l'entrée via le réseau.
- Calculez la perte (dans quelle mesure la sortie est-elle correcte).
- Propagez les dégradés dans les paramètres du réseau.
- Mettez à jour les poids du réseau, généralement en utilisant une simple mise à jour comme indiqué ci-dessous
rule: weight = weight -learning_rate * gradientL'intelligence artificielle est à la mode de nos jours dans une plus grande mesure. L'apprentissage automatique et l'apprentissage profond constituent l'intelligence artificielle. Le diagramme de Venn mentionné ci-dessous explique la relation entre l'apprentissage automatique et l'apprentissage en profondeur.

Apprentissage automatique
L'apprentissage automatique est l'art de la science qui permet aux ordinateurs d'agir selon les algorithmes conçus et programmés. De nombreux chercheurs pensent que l'apprentissage automatique est le meilleur moyen de progresser vers l'IA au niveau humain. Il comprend divers types de modèles comme -
- Modèle d'apprentissage supervisé
- Modèle d'apprentissage non supervisé
L'apprentissage en profondeur
L'apprentissage profond est un sous-domaine de l'apprentissage automatique dans lequel les algorithmes concernés sont inspirés de la structure et de la fonction du cerveau appelées réseaux de neurones artificiels.
L'apprentissage en profondeur a gagné beaucoup d'importance grâce à l'apprentissage supervisé ou à l'apprentissage à partir de données et d'algorithmes étiquetés. Chaque algorithme de l'apprentissage profond passe par le même processus. Il inclut la hiérarchie de la transformation non linéaire de l'entrée et utilise pour créer un modèle statistique en tant que sortie.
Le processus d'apprentissage automatique est défini à l'aide des étapes suivantes:
- Identifie les ensembles de données pertinents et les prépare pour l'analyse.
- Choisit le type d'algorithme à utiliser.
- Construit un modèle analytique basé sur l'algorithme utilisé.
- Entraîne le modèle sur des ensembles de données de test, en le révisant si nécessaire.
- Exécute le modèle pour générer des scores de test.
Dans ce chapitre, nous discuterons de la différence majeure entre les concepts d'apprentissage automatique et d'apprentissage en profondeur.
Quantité de données
L'apprentissage automatique fonctionne avec différentes quantités de données et est principalement utilisé pour de petites quantités de données. Le Deep Learning, quant à lui, fonctionne efficacement si la quantité de données augmente rapidement. Le diagramme suivant illustre le fonctionnement de l'apprentissage automatique et de l'apprentissage en profondeur par rapport à la quantité de données -

Dépendances matérielles
Les algorithmes d'apprentissage en profondeur sont conçus pour dépendre fortement des machines haut de gamme contrairement aux algorithmes d'apprentissage automatique traditionnels. Les algorithmes d'apprentissage profond effectuent un grand nombre d'opérations de multiplication matricielle qui nécessitent un support matériel énorme.
Ingénierie des fonctionnalités
L'ingénierie des fonctionnalités est le processus consistant à intégrer les connaissances du domaine dans des fonctionnalités spécifiées pour réduire la complexité des données et créer des modèles visibles pour les algorithmes d'apprentissage.
Par exemple, les modèles d'apprentissage automatique traditionnels se concentrent sur les pixels et d'autres attributs nécessaires au processus d'ingénierie des fonctionnalités. Les algorithmes d'apprentissage en profondeur se concentrent sur les fonctionnalités de haut niveau à partir des données. Cela réduit la tâche de développement d'un nouvel extracteur de fonctionnalités pour chaque nouveau problème.
PyTorch comprend une fonction spéciale de création et de mise en œuvre de réseaux de neurones. Dans ce chapitre, nous allons créer un réseau de neurones simple avec une couche cachée développant une seule unité de sortie.
Nous utiliserons les étapes suivantes pour implémenter le premier réseau de neurones en utilisant PyTorch -
Étape 1
Tout d'abord, nous devons importer la bibliothèque PyTorch en utilisant la commande ci-dessous -
import torch
import torch.nn as nnÉtape 2
Définissez toutes les couches et la taille du lot pour commencer à exécuter le réseau neuronal comme indiqué ci-dessous -
# Defining input size, hidden layer size, output size and batch size respectively
n_in, n_h, n_out, batch_size = 10, 5, 1, 10Étape 3
Comme le réseau neuronal comprend une combinaison de données d'entrée pour obtenir les données de sortie respectives, nous suivrons la même procédure que celle indiquée ci-dessous -
# Create dummy input and target tensors (data)
x = torch.randn(batch_size, n_in)
y = torch.tensor([[1.0], [0.0], [0.0],
[1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])Étape 4
Créez un modèle séquentiel à l'aide de fonctions intégrées. En utilisant les lignes de code ci-dessous, créez un modèle séquentiel -
# Create a model
model = nn.Sequential(nn.Linear(n_in, n_h),
nn.ReLU(),
nn.Linear(n_h, n_out),
nn.Sigmoid())Étape 5
Construisez la fonction de perte à l'aide de l'optimiseur Gradient Descent comme indiqué ci-dessous -
Construct the loss function
criterion = torch.nn.MSELoss()
# Construct the optimizer (Stochastic Gradient Descent in this case)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)Étape 6
Implémentez le modèle de descente de gradient avec la boucle itérante avec les lignes de code données -
# Gradient Descent
for epoch in range(50):
# Forward pass: Compute predicted y by passing x to the model
y_pred = model(x)
# Compute and print loss
loss = criterion(y_pred, y)
print('epoch: ', epoch,' loss: ', loss.item())
# Zero gradients, perform a backward pass, and update the weights.
optimizer.zero_grad()
# perform a backward pass (backpropagation)
loss.backward()
# Update the parameters
optimizer.step()Étape 7
La sortie générée est la suivante -
epoch: 0 loss: 0.2545787990093231
epoch: 1 loss: 0.2545052170753479
epoch: 2 loss: 0.254431813955307
epoch: 3 loss: 0.25435858964920044
epoch: 4 loss: 0.2542854845523834
epoch: 5 loss: 0.25421255826950073
epoch: 6 loss: 0.25413978099823
epoch: 7 loss: 0.25406715273857117
epoch: 8 loss: 0.2539947032928467
epoch: 9 loss: 0.25392240285873413
epoch: 10 loss: 0.25385022163391113
epoch: 11 loss: 0.25377824902534485
epoch: 12 loss: 0.2537063956260681
epoch: 13 loss: 0.2536346912384033
epoch: 14 loss: 0.25356316566467285
epoch: 15 loss: 0.25349172949790955
epoch: 16 loss: 0.25342053174972534
epoch: 17 loss: 0.2533493936061859
epoch: 18 loss: 0.2532784342765808
epoch: 19 loss: 0.25320762395858765
epoch: 20 loss: 0.2531369626522064
epoch: 21 loss: 0.25306645035743713
epoch: 22 loss: 0.252996027469635
epoch: 23 loss: 0.2529257833957672
epoch: 24 loss: 0.25285571813583374
epoch: 25 loss: 0.25278574228286743
epoch: 26 loss: 0.25271597504615784
epoch: 27 loss: 0.25264623761177063
epoch: 28 loss: 0.25257670879364014
epoch: 29 loss: 0.2525072991847992
epoch: 30 loss: 0.2524380087852478
epoch: 31 loss: 0.2523689270019531
epoch: 32 loss: 0.25229987502098083
epoch: 33 loss: 0.25223103165626526
epoch: 34 loss: 0.25216227769851685
epoch: 35 loss: 0.252093642950058
epoch: 36 loss: 0.25202515721321106
epoch: 37 loss: 0.2519568204879761
epoch: 38 loss: 0.251888632774353
epoch: 39 loss: 0.25182053446769714
epoch: 40 loss: 0.2517525553703308
epoch: 41 loss: 0.2516847252845764
epoch: 42 loss: 0.2516169846057892
epoch: 43 loss: 0.2515493929386139
epoch: 44 loss: 0.25148195028305054
epoch: 45 loss: 0.25141456723213196
epoch: 46 loss: 0.2513473629951477
epoch: 47 loss: 0.2512802183628082
epoch: 48 loss: 0.2512132525444031
epoch: 49 loss: 0.2511464059352875La formation d'un algorithme d'apprentissage en profondeur implique les étapes suivantes -
- Construire un pipeline de données
- Construire une architecture de réseau
- Évaluation de l'architecture à l'aide d'une fonction de perte
- Optimiser les pondérations de l'architecture du réseau à l'aide d'un algorithme d'optimisation
La formation d'un algorithme d'apprentissage en profondeur spécifique est l'exigence exacte de la conversion d'un réseau neuronal en blocs fonctionnels, comme indiqué ci-dessous -

En ce qui concerne le diagramme ci-dessus, tout algorithme d'apprentissage en profondeur implique l'obtention des données d'entrée, la construction de l'architecture respective qui comprend un ensemble de couches intégrées.
Si vous observez le diagramme ci-dessus, la précision est évaluée à l'aide d'une fonction de perte par rapport à l'optimisation des poids du réseau neuronal.
Dans ce chapitre, nous discuterons de certains des termes les plus couramment utilisés dans PyTorch.
NumPy PyTorch
Un tenseur PyTorch est identique à un tableau NumPy. Un tenseur est un tableau à n dimensions et par rapport à PyTorch, il fournit de nombreuses fonctions pour opérer sur ces tenseurs.
Les tenseurs PyTorch utilisent généralement des GPU pour accélérer leurs calculs numériques. Ces tenseurs créés dans PyTorch peuvent être utilisés pour adapter un réseau à deux couches à des données aléatoires. L'utilisateur peut implémenter manuellement les passages avant et arrière sur le réseau.
Variables et Autograd
Lors de l'utilisation d'autograd, le passage avant de votre réseau définira un computational graph - les nœuds du graphique seront des Tensors, et les arêtes seront des fonctions qui produisent des Tensors de sortie à partir des Tensors d'entrée.
Les Tensors PyTorch peuvent être créés en tant qu'objets variables où une variable représente un nœud dans un graphe de calcul.
Graphiques dynamiques
Les graphiques statiques sont agréables car l'utilisateur peut optimiser le graphique à l'avance. Si les programmeurs réutilisent le même graphique encore et encore, alors cette optimisation initiale potentiellement coûteuse peut être maintenue car le même graphique est réexécuté encore et encore.
La principale différence entre eux est que les graphes de calcul de Tensor Flow sont statiques et PyTorch utilise des graphes de calcul dynamiques.
Paquet Optim
Le package optim de PyTorch résume l'idée d'un algorithme d'optimisation qui est implémenté de nombreuses manières et fournit des illustrations d'algorithmes d'optimisation couramment utilisés. Cela peut être appelé dans l'instruction d'importation.
Multitraitement
Le multitraitement prend en charge les mêmes opérations, de sorte que tous les tenseurs fonctionnent sur plusieurs processeurs. La file d'attente verra ses données déplacées dans la mémoire partagée et n'enverra un descripteur qu'à un autre processus.
PyTorch comprend un package appelé torchvision qui est utilisé pour charger et préparer l'ensemble de données. Il comprend deux fonctions de base à savoir Dataset et DataLoader qui aide à la transformation et au chargement de l'ensemble de données.
Base de données
L'ensemble de données est utilisé pour lire et transformer un point de données à partir de l'ensemble de données donné. La syntaxe de base à implémenter est mentionnée ci-dessous -
trainset = torchvision.datasets.CIFAR10(root = './data', train = True,
download = True, transform = transform)DataLoader est utilisé pour mélanger et regrouper les données. Il peut être utilisé pour charger les données en parallèle avec des nœuds de calcul multitraitement.
trainloader = torch.utils.data.DataLoader(trainset, batch_size = 4,
shuffle = True, num_workers = 2)Exemple: chargement d'un fichier CSV
Nous utilisons le package Python Panda pour charger le fichier csv. Le fichier d'origine a le format suivant: (nom de l'image, 68 points de repère - chaque point de repère a des coordonnées ax, y).
landmarks_frame = pd.read_csv('faces/face_landmarks.csv')
n = 65
img_name = landmarks_frame.iloc[n, 0]
landmarks = landmarks_frame.iloc[n, 1:].as_matrix()
landmarks = landmarks.astype('float').reshape(-1, 2)Dans ce chapitre, nous nous concentrerons sur un exemple de base d'implémentation de régression linéaire à l'aide de TensorFlow. La régression logistique ou régression linéaire est une approche d'apprentissage automatique supervisé pour la classification des catégories discrètes d'ordre. Notre objectif dans ce chapitre est de construire un modèle par lequel un utilisateur peut prédire la relation entre les variables prédictives et une ou plusieurs variables indépendantes.
La relation entre ces deux variables est considérée comme linéaire, c'est-à-dire que si y est la variable dépendante et x est considéré comme la variable indépendante, alors la relation de régression linéaire de deux variables ressemblera à l'équation mentionnée ci-dessous -
Y = Ax+bEnsuite, nous allons concevoir un algorithme de régression linéaire qui nous permet de comprendre deux concepts importants donnés ci-dessous -
- Fonction de coût
- Algorithmes de descente de gradient
La représentation schématique de la régression linéaire est mentionnée ci-dessous
Interpréter le résultat
$$ Y = ax + b $$
La valeur de a est la pente.
La valeur de b est le y − intercept.
r est le correlation coefficient.
r2 est le correlation coefficient.
La vue graphique de l'équation de régression linéaire est mentionnée ci-dessous -

Les étapes suivantes sont utilisées pour implémenter la régression linéaire à l'aide de PyTorch -
Étape 1
Importez les packages nécessaires pour créer une régression linéaire dans PyTorch en utilisant le code ci-dessous -
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline
sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = TrueÉtape 2
Créez un seul ensemble d'entraînement avec l'ensemble de données disponible, comme indiqué ci-dessous -
m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)
noise = np.random.randn(256) / 4
y = x * m + c + noise
df = pd.DataFrame()
df['x'] = x
df['y'] = y
sns.lmplot(x ='x', y ='y', data = df)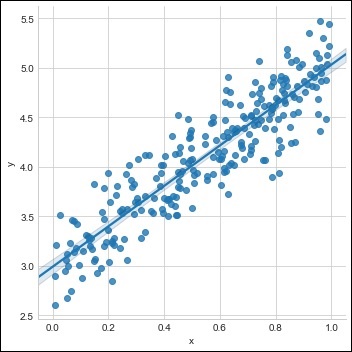
Étape 3
Implémentez la régression linéaire avec les bibliothèques PyTorch comme mentionné ci-dessous -
import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')
class LinearRegressionModel(nn.Module):
def __init__(self, input_dim, output_dim):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(input_dim, output_dim)
def forward(self, x):
out = self.linear(x)
return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()
def get_param_values():
return w.data[0][0], b.data[0]
def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')Le tracé généré est le suivant -

L'apprentissage en profondeur est une division de l'apprentissage automatique et est considéré comme une étape cruciale franchie par les chercheurs au cours des dernières décennies. Les exemples de mise en œuvre de l'apprentissage en profondeur incluent des applications telles que la reconnaissance d'image et la reconnaissance vocale.
Les deux types importants de réseaux de neurones profonds sont donnés ci-dessous -
- Réseaux de neurones convolutifs
- Réseaux de neurones récurrents.
Dans ce chapitre, nous nous concentrerons sur le premier type, à savoir les réseaux de neurones convolutifs (CNN).
Réseaux de neurones convolutifs
Les réseaux de neurones convolutifs sont conçus pour traiter les données à travers plusieurs couches de tableaux. Ce type de réseaux neuronaux est utilisé dans des applications telles que la reconnaissance d'image ou la reconnaissance faciale.
La principale différence entre CNN et tout autre réseau de neurones ordinaire est que CNN prend les entrées sous forme de tableau bidimensionnel et opère directement sur les images plutôt que de se concentrer sur l'extraction de caractéristiques sur laquelle se concentrent d'autres réseaux de neurones.
L'approche dominante de CNN inclut la solution aux problèmes de reconnaissance. Des entreprises de premier plan comme Google et Facebook ont investi dans des projets de recherche et de développement de projets de reconnaissance pour mener à bien leurs activités plus rapidement.
Chaque réseau neuronal convolutif comprend trois idées de base -
- Champs respectifs locaux
- Convolution
- Pooling
Comprenons chacune de ces terminologies en détail.
Champs respectifs locaux
CNN utilise des corrélations spatiales qui existent dans les données d'entrée. Chacun dans les couches concurrentes des réseaux de neurones se connecte à certains neurones d'entrée. Cette région spécifique est appelée champ réceptif local. Il se concentre uniquement sur les neurones cachés. Le neurone caché traitera les données d'entrée à l'intérieur du champ mentionné sans réaliser les changements en dehors de la limite spécifique.
La représentation schématique de la génération des champs respectifs locaux est mentionnée ci-dessous -

Convolution
Dans la figure ci-dessus, nous observons que chaque connexion apprend un poids de neurone caché avec une connexion associée avec le mouvement d'une couche à l'autre. Ici, les neurones individuels effectuent un changement de temps en temps. Ce processus est appelé «convolution».
Le mappage des connexions de la couche d'entrée à la carte d'entités cachées est défini comme des «pondérations partagées» et le biais inclus est appelé «biais partagé».
mise en commun
Les réseaux de neurones convolutifs utilisent des couches de regroupement qui sont positionnées immédiatement après la déclaration CNN. Il prend les entrées de l'utilisateur comme une carte des caractéristiques qui sort des réseaux convolutifs et prépare une carte des caractéristiques condensée. La mise en commun des couches aide à créer des couches avec des neurones des couches précédentes.
Implémentation de PyTorch
Les étapes suivantes sont utilisées pour créer un réseau neuronal convolutif à l'aide de PyTorch.
Étape 1
Importez les packages nécessaires pour créer un réseau de neurones simple.
from torch.autograd import Variable
import torch.nn.functional as FÉtape 2
Créez une classe avec une représentation par lots du réseau neuronal convolutif. Notre forme de lot pour l'entrée x est de dimension (3, 32, 32).
class SimpleCNN(torch.nn.Module):
def __init__(self):
super(SimpleCNN, self).__init__()
#Input channels = 3, output channels = 18
self.conv1 = torch.nn.Conv2d(3, 18, kernel_size = 3, stride = 1, padding = 1)
self.pool = torch.nn.MaxPool2d(kernel_size = 2, stride = 2, padding = 0)
#4608 input features, 64 output features (see sizing flow below)
self.fc1 = torch.nn.Linear(18 * 16 * 16, 64)
#64 input features, 10 output features for our 10 defined classes
self.fc2 = torch.nn.Linear(64, 10)Étape 3
Calculez l'activation des premiers changements de taille de convolution de (3, 32, 32) à (18, 32, 32).
La taille de la dimension passe de (18, 32, 32) à (18, 16, 16). Remodeler la dimension des données de la couche d'entrée du réseau neuronal en raison de laquelle la taille passe de (18, 16, 16) à (1, 4608).
Rappelons que -1 déduit cette dimension de l'autre dimension donnée.
def forward(self, x):
x = F.relu(self.conv1(x))
x = self.pool(x)
x = x.view(-1, 18 * 16 *16)
x = F.relu(self.fc1(x))
#Computes the second fully connected layer (activation applied later)
#Size changes from (1, 64) to (1, 10)
x = self.fc2(x)
return(x)Les réseaux de neurones récurrents sont un type d'algorithme axé sur l'apprentissage profond qui suit une approche séquentielle. Dans les réseaux de neurones, nous supposons toujours que chaque entrée et sortie est indépendante de toutes les autres couches. Ces types de réseaux de neurones sont appelés récurrents car ils effectuent des calculs mathématiques de manière séquentielle en complétant une tâche après l'autre.
Le schéma ci-dessous spécifie l'approche complète et le fonctionnement des réseaux de neurones récurrents -

Sur la figure ci-dessus, c1, c2, c3 et x1 sont considérés comme des entrées qui comprennent certaines valeurs d'entrée cachées à savoir h1, h2 et h3 délivrant la sortie respective de o1. Nous allons maintenant nous concentrer sur la mise en œuvre de PyTorch pour créer une onde sinusoïdale à l'aide de réseaux de neurones récurrents.
Pendant la formation, nous suivrons une approche de formation de notre modèle avec un point de données à la fois. La séquence d'entrée x se compose de 20 points de données et la séquence cible est considérée comme la même que la séquence d'entrée.
Étape 1
Importez les packages nécessaires pour implémenter des réseaux de neurones récurrents en utilisant le code ci-dessous -
import torch
from torch.autograd import Variable
import numpy as np
import pylab as pl
import torch.nn.init as initÉtape 2
Nous allons définir les hyper paramètres du modèle avec la taille de la couche d'entrée fixée à 7. Il y aura 6 neurones de contexte et 1 neurone d'entrée pour créer la séquence cible.
dtype = torch.FloatTensor
input_size, hidden_size, output_size = 7, 6, 1
epochs = 300
seq_length = 20
lr = 0.1
data_time_steps = np.linspace(2, 10, seq_length + 1)
data = np.sin(data_time_steps)
data.resize((seq_length + 1, 1))
x = Variable(torch.Tensor(data[:-1]).type(dtype), requires_grad=False)
y = Variable(torch.Tensor(data[1:]).type(dtype), requires_grad=False)Nous allons générer des données d'entraînement, où x est la séquence de données d'entrée et y est la séquence cible requise.
Étape 3
Les poids sont initialisés dans le réseau neuronal récurrent en utilisant une distribution normale avec une moyenne nulle. W1 représentera l'acceptation des variables d'entrée et w2 représentera la sortie qui est générée comme indiqué ci-dessous -
w1 = torch.FloatTensor(input_size,
hidden_size).type(dtype)
init.normal(w1, 0.0, 0.4)
w1 = Variable(w1, requires_grad = True)
w2 = torch.FloatTensor(hidden_size, output_size).type(dtype)
init.normal(w2, 0.0, 0.3)
w2 = Variable(w2, requires_grad = True)Étape 4
Maintenant, il est important de créer une fonction de feed-back qui définit de manière unique le réseau neuronal.
def forward(input, context_state, w1, w2):
xh = torch.cat((input, context_state), 1)
context_state = torch.tanh(xh.mm(w1))
out = context_state.mm(w2)
return (out, context_state)Étape 5
L'étape suivante consiste à démarrer la procédure de formation de l'implémentation de l'onde sinusoïdale récurrente du réseau neuronal. La boucle externe parcourt chaque boucle et la boucle interne parcourt l'élément de séquence. Ici, nous allons également calculer l'erreur quadratique moyenne (MSE) qui aide à la prédiction des variables continues.
for i in range(epochs):
total_loss = 0
context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = True)
for j in range(x.size(0)):
input = x[j:(j+1)]
target = y[j:(j+1)]
(pred, context_state) = forward(input, context_state, w1, w2)
loss = (pred - target).pow(2).sum()/2
total_loss += loss
loss.backward()
w1.data -= lr * w1.grad.data
w2.data -= lr * w2.grad.data
w1.grad.data.zero_()
w2.grad.data.zero_()
context_state = Variable(context_state.data)
if i % 10 == 0:
print("Epoch: {} loss {}".format(i, total_loss.data[0]))
context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = False)
predictions = []
for i in range(x.size(0)):
input = x[i:i+1]
(pred, context_state) = forward(input, context_state, w1, w2)
context_state = context_state
predictions.append(pred.data.numpy().ravel()[0])Étape 6
Maintenant, il est temps de tracer l'onde sinusoïdale selon les besoins.
pl.scatter(data_time_steps[:-1], x.data.numpy(), s = 90, label = "Actual")
pl.scatter(data_time_steps[1:], predictions, label = "Predicted")
pl.legend()
pl.show()Production
La sortie pour le processus ci-dessus est la suivante -

Dans ce chapitre, nous nous concentrerons davantage sur torchvision.datasetset ses différents types. PyTorch comprend les chargeurs de jeux de données suivants -
- MNIST
- COCO (sous-titrage et détection)
L'ensemble de données comprend la majorité des deux types de fonctions donnés ci-dessous -
Transform- une fonction qui prend dans une image et renvoie une version modifiée de trucs standard. Ceux-ci peuvent être composés avec des transformations.
Target_transform- une fonction qui prend la cible et la transforme. Par exemple, prend la chaîne de légende et renvoie un tenseur d'indices mondiaux.
MNIST
Voici l'exemple de code pour l'ensemble de données MNIST -
dset.MNIST(root, train = TRUE, transform = NONE,
target_transform = None, download = FALSE)Les paramètres sont les suivants -
root - répertoire racine de l'ensemble de données où existent des données traitées.
train - Vrai = ensemble d'entraînement, Faux = ensemble de test
download - True = télécharge l'ensemble de données d'Internet et le place à la racine.
COCO
Cela nécessite l'installation de l'API COCO. L'exemple suivant est utilisé pour démontrer l'implémentation COCO d'un ensemble de données à l'aide de PyTorch -
import torchvision.dataset as dset
import torchvision.transforms as transforms
cap = dset.CocoCaptions(root = ‘ dir where images are’,
annFile = ’json annotation file’,
transform = transforms.ToTensor())
print(‘Number of samples: ‘, len(cap))
print(target)Le résultat obtenu est le suivant -
Number of samples: 82783
Image Size: (3L, 427L, 640L)Les couvents consistent à construire le modèle CNN à partir de zéro. L'architecture du réseau contiendra une combinaison des étapes suivantes -
- Conv2d
- MaxPool2d
- Unité linéaire rectifiée
- View
- Couche linéaire
Entraîner le modèle
La formation du modèle est le même processus que les problèmes de classification d'image. L'extrait de code suivant complète la procédure d'un modèle d'entraînement sur l'ensemble de données fourni -
def fit(epoch,model,data_loader,phase
= 'training',volatile = False):
if phase == 'training':
model.train()
if phase == 'training':
model.train()
if phase == 'validation':
model.eval()
volatile=True
running_loss = 0.0
running_correct = 0
for batch_idx , (data,target) in enumerate(data_loader):
if is_cuda:
data,target = data.cuda(),target.cuda()
data , target = Variable(data,volatile),Variable(target)
if phase == 'training':
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output,target)
running_loss + =
F.nll_loss(output,target,size_average =
False).data[0]
preds = output.data.max(dim = 1,keepdim = True)[1]
running_correct + =
preds.eq(target.data.view_as(preds)).cpu().sum()
if phase == 'training':
loss.backward()
optimizer.step()
loss = running_loss/len(data_loader.dataset)
accuracy = 100. * running_correct/len(data_loader.dataset)
print(f'{phase} loss is {loss:{5}.{2}} and {phase} accuracy is {running_correct}/{len(data_loader.dataset)}{accuracy:{return loss,accuracy}})La méthode comprend différentes logiques pour la formation et la validation. Il y a deux raisons principales pour utiliser différents modes -
En mode train, l'abandon supprime un pourcentage de valeurs, ce qui ne devrait pas se produire lors de la phase de validation ou de test.
Pour le mode d'apprentissage, nous calculons les gradients et modifions la valeur des paramètres du modèle, mais la rétro-propagation n'est pas nécessaire pendant les phases de test ou de validation.
Dans ce chapitre, nous nous concentrerons sur la création d'un couvent à partir de rien. Cela implique la création du couvent ou de l'échantillon de réseau neuronal respectif avec une torche.
Étape 1
Créez une classe nécessaire avec les paramètres respectifs. Les paramètres incluent des poids avec une valeur aléatoire.
class Neural_Network(nn.Module):
def __init__(self, ):
super(Neural_Network, self).__init__()
self.inputSize = 2
self.outputSize = 1
self.hiddenSize = 3
# weights
self.W1 = torch.randn(self.inputSize,
self.hiddenSize) # 3 X 2 tensor
self.W2 = torch.randn(self.hiddenSize, self.outputSize) # 3 X 1 tensorÉtape 2
Créez un modèle de fonction en aval avec des fonctions sigmoïdes.
def forward(self, X):
self.z = torch.matmul(X, self.W1) # 3 X 3 ".dot"
does not broadcast in PyTorch
self.z2 = self.sigmoid(self.z) # activation function
self.z3 = torch.matmul(self.z2, self.W2)
o = self.sigmoid(self.z3) # final activation
function
return o
def sigmoid(self, s):
return 1 / (1 + torch.exp(-s))
def sigmoidPrime(self, s):
# derivative of sigmoid
return s * (1 - s)
def backward(self, X, y, o):
self.o_error = y - o # error in output
self.o_delta = self.o_error * self.sigmoidPrime(o) # derivative of sig to error
self.z2_error = torch.matmul(self.o_delta, torch.t(self.W2))
self.z2_delta = self.z2_error * self.sigmoidPrime(self.z2)
self.W1 + = torch.matmul(torch.t(X), self.z2_delta)
self.W2 + = torch.matmul(torch.t(self.z2), self.o_delta)Étape 3
Créez un modèle de formation et de prédiction comme indiqué ci-dessous -
def train(self, X, y):
# forward + backward pass for training
o = self.forward(X)
self.backward(X, y, o)
def saveWeights(self, model):
# Implement PyTorch internal storage functions
torch.save(model, "NN")
# you can reload model with all the weights and so forth with:
# torch.load("NN")
def predict(self):
print ("Predicted data based on trained weights: ")
print ("Input (scaled): \n" + str(xPredicted))
print ("Output: \n" + str(self.forward(xPredicted)))Les réseaux de neurones convolutifs incluent une caractéristique principale, extraction. Les étapes suivantes sont utilisées pour implémenter l'extraction de caractéristiques du réseau neuronal convolutif.
Étape 1
Importez les modèles respectifs pour créer le modèle d'extraction d'entités avec «PyTorch».
import torch
import torch.nn as nn
from torchvision import modelsÉtape 2
Créez une classe d'extraction de fonctionnalités qui peut être appelée en cas de besoin.
class Feature_extractor(nn.module):
def forward(self, input):
self.feature = input.clone()
return input
new_net = nn.Sequential().cuda() # the new network
target_layers = [conv_1, conv_2, conv_4] # layers you want to extract`
i = 1
for layer in list(cnn):
if isinstance(layer,nn.Conv2d):
name = "conv_"+str(i)
art_net.add_module(name,layer)
if name in target_layers:
new_net.add_module("extractor_"+str(i),Feature_extractor())
i+=1
if isinstance(layer,nn.ReLU):
name = "relu_"+str(i)
new_net.add_module(name,layer)
if isinstance(layer,nn.MaxPool2d):
name = "pool_"+str(i)
new_net.add_module(name,layer)
new_net.forward(your_image)
print (new_net.extractor_3.feature)Dans ce chapitre, nous nous concentrerons sur le modèle de visualisation des données à l'aide de couvents. Les étapes suivantes sont nécessaires pour obtenir une image parfaite de la visualisation avec un réseau neuronal conventionnel.
Étape 1
Importez les modules nécessaires, ce qui est important pour la visualisation des réseaux de neurones conventionnels.
import os
import numpy as np
import pandas as pd
from scipy.misc import imread
from sklearn.metrics import accuracy_score
import keras
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Flatten, Activation, Input
from keras.layers import Conv2D, MaxPooling2D
import torchÉtape 2
Pour arrêter le hasard potentiel avec les données d'entraînement et de test, appelez l'ensemble de données respectif comme indiqué dans le code ci-dessous -
seed = 128
rng = np.random.RandomState(seed)
data_dir = "../../datasets/MNIST"
train = pd.read_csv('../../datasets/MNIST/train.csv')
test = pd.read_csv('../../datasets/MNIST/Test_fCbTej3.csv')
img_name = rng.choice(train.filename)
filepath = os.path.join(data_dir, 'train', img_name)
img = imread(filepath, flatten=True)Étape 3
Tracez les images nécessaires pour obtenir les données d'entraînement et de test définies de manière parfaite en utilisant le code ci-dessous -
pylab.imshow(img, cmap ='gray')
pylab.axis('off')
pylab.show()La sortie est affichée comme ci-dessous -

Dans ce chapitre, nous proposons une approche alternative qui repose plutôt sur un seul réseau de neurones convolutifs 2D sur les deux séquences. Chaque couche de notre réseau recode les jetons source sur la base de la séquence de sortie produite jusqu'à présent. Les propriétés de type attention sont donc omniprésentes dans tout le réseau.
Ici, nous allons nous concentrer sur creating the sequential network with specific pooling from the values included in dataset. Ce processus est également mieux appliqué dans «Module de reconnaissance d'image».

Les étapes suivantes sont utilisées pour créer un modèle de traitement de séquence avec des couvents à l'aide de PyTorch -
Étape 1
Importez les modules nécessaires à l'exécution du traitement séquentiel à l'aide de couvents.
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
import numpy as npÉtape 2
Effectuez les opérations nécessaires pour créer un motif dans l'ordre respectif en utilisant le code ci-dessous -
batch_size = 128
num_classes = 10
epochs = 12
# input image dimensions
img_rows, img_cols = 28, 28
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000,28,28,1)
x_test = x_test.reshape(10000,28,28,1)
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)Étape 3
Compilez le modèle et ajustez le modèle dans le modèle de réseau neuronal conventionnel mentionné comme indiqué ci-dessous -
model.compile(loss =
keras.losses.categorical_crossentropy,
optimizer = keras.optimizers.Adadelta(), metrics =
['accuracy'])
model.fit(x_train, y_train,
batch_size = batch_size, epochs = epochs,
verbose = 1, validation_data = (x_test, y_test))
score = model.evaluate(x_test, y_test, verbose = 0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])La sortie générée est la suivante -

Dans ce chapitre, nous allons comprendre le célèbre modèle d'intégration de mots - word2vec. Le modèle Word2vec est utilisé pour produire l'incorporation de mots à l'aide d'un groupe de modèles associés. Le modèle Word2vec est implémenté avec du code C pur et le gradient est calculé manuellement.
L'implémentation du modèle word2vec dans PyTorch est expliquée dans les étapes ci-dessous -
Étape 1
Implémentez les bibliothèques dans l'incorporation de mots comme mentionné ci-dessous -
import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as FÉtape 2
Implémentez le modèle Skip Gram d'incorporation de mots avec la classe appelée word2vec. Il comprendemb_size, emb_dimension, u_embedding, v_embedding type d'attributs.
class SkipGramModel(nn.Module):
def __init__(self, emb_size, emb_dimension):
super(SkipGramModel, self).__init__()
self.emb_size = emb_size
self.emb_dimension = emb_dimension
self.u_embeddings = nn.Embedding(emb_size, emb_dimension, sparse=True)
self.v_embeddings = nn.Embedding(emb_size, emb_dimension, sparse = True)
self.init_emb()
def init_emb(self):
initrange = 0.5 / self.emb_dimension
self.u_embeddings.weight.data.uniform_(-initrange, initrange)
self.v_embeddings.weight.data.uniform_(-0, 0)
def forward(self, pos_u, pos_v, neg_v):
emb_u = self.u_embeddings(pos_u)
emb_v = self.v_embeddings(pos_v)
score = torch.mul(emb_u, emb_v).squeeze()
score = torch.sum(score, dim = 1)
score = F.logsigmoid(score)
neg_emb_v = self.v_embeddings(neg_v)
neg_score = torch.bmm(neg_emb_v, emb_u.unsqueeze(2)).squeeze()
neg_score = F.logsigmoid(-1 * neg_score)
return -1 * (torch.sum(score)+torch.sum(neg_score))
def save_embedding(self, id2word, file_name, use_cuda):
if use_cuda:
embedding = self.u_embeddings.weight.cpu().data.numpy()
else:
embedding = self.u_embeddings.weight.data.numpy()
fout = open(file_name, 'w')
fout.write('%d %d\n' % (len(id2word), self.emb_dimension))
for wid, w in id2word.items():
e = embedding[wid]
e = ' '.join(map(lambda x: str(x), e))
fout.write('%s %s\n' % (w, e))
def test():
model = SkipGramModel(100, 100)
id2word = dict()
for i in range(100):
id2word[i] = str(i)
model.save_embedding(id2word)Étape 3
Implémentez la méthode principale pour afficher correctement le modèle d'incorporation de mots.
if __name__ == '__main__':
test()Les réseaux de neurones profonds ont une fonctionnalité exclusive pour permettre des percées dans l'apprentissage automatique en comprenant le processus du langage naturel. On observe que la plupart de ces modèles traitent le langage comme une séquence plate de mots ou de caractères, et utilisent une sorte de modèle qui est appelé réseau neuronal récurrent ou RNN.
De nombreux chercheurs arrivent à la conclusion que la langue est mieux comprise par rapport à l'arbre hiérarchique des phrases. Ce type est inclus dans les réseaux de neurones récursifs qui prennent en compte une structure spécifique.
PyTorch a une fonctionnalité spécifique qui permet de rendre ces modèles complexes de traitement du langage naturel beaucoup plus faciles. Il s'agit d'un cadre complet pour tous les types d'apprentissage en profondeur avec un support solide pour la vision par ordinateur.
Caractéristiques du réseau neuronal récursif
Un réseau de neurones récursif est créé de telle manière qu'il inclut l'application du même ensemble de poids avec différentes structures de type graphique.
Les nœuds sont parcourus dans l'ordre topologique.
Ce type de réseau est formé par le mode inverse de différenciation automatique.
Le traitement du langage naturel comprend un cas particulier de réseaux de neurones récursifs.
Ce réseau de tenseur neuronal récursif comprend divers nœuds fonctionnels de composition dans l'arbre.
L'exemple du réseau de neurones récursif est illustré ci-dessous -
