R - Distribution binomiale
Le modèle de distribution binomiale traite de la recherche de la probabilité de succès d'un événement qui n'a que deux résultats possibles dans une série d'expériences. Par exemple, lancer une pièce donne toujours une tête ou une queue. La probabilité de trouver exactement 3 têtes en lançant une pièce à plusieurs reprises pendant 10 fois est estimée pendant la distribution binomiale.
R a quatre fonctions intégrées pour générer une distribution binomiale. Ils sont décrits ci-dessous.
dbinom(x, size, prob)
pbinom(x, size, prob)
qbinom(p, size, prob)
rbinom(n, size, prob)Voici la description des paramètres utilisés -
x est un vecteur de nombres.
p est un vecteur de probabilités.
n est le nombre d'observations.
size est le nombre d'essais.
prob est la probabilité de succès de chaque essai.
dbinom ()
Cette fonction donne la distribution de densité de probabilité à chaque point.
# Create a sample of 50 numbers which are incremented by 1.
x <- seq(0,50,by = 1)
# Create the binomial distribution.
y <- dbinom(x,50,0.5)
# Give the chart file a name.
png(file = "dbinom.png")
# Plot the graph for this sample.
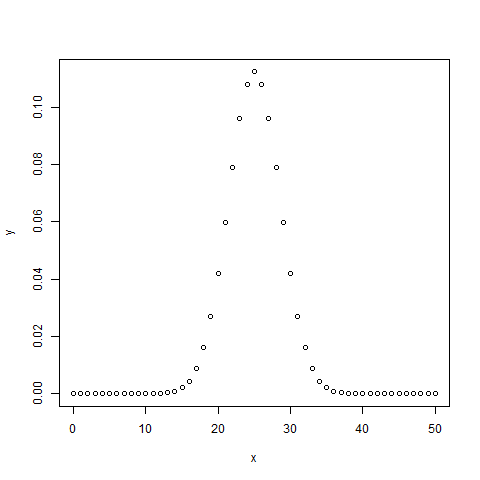
plot(x,y)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
pbinom ()
Cette fonction donne la probabilité cumulée d'un événement. C'est une valeur unique représentant la probabilité.
# Probability of getting 26 or less heads from a 51 tosses of a coin.
x <- pbinom(26,51,0.5)
print(x)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 0.610116qbinom ()
Cette fonction prend la valeur de probabilité et donne un nombre dont la valeur cumulée correspond à la valeur de probabilité.
# How many heads will have a probability of 0.25 will come out when a coin
# is tossed 51 times.
x <- qbinom(0.25,51,1/2)
print(x)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 23rbinom ()
Cette fonction génère le nombre requis de valeurs aléatoires d'une probabilité donnée à partir d'un échantillon donné.
# Find 8 random values from a sample of 150 with probability of 0.4.
x <- rbinom(8,150,.4)
print(x)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 58 61 59 66 55 60 61 67