R - Guide rapide
R est un langage de programmation et un environnement logiciel pour l'analyse statistique, la représentation graphique et le reporting. R a été créé par Ross Ihaka et Robert Gentleman à l'Université d'Auckland, en Nouvelle-Zélande, et est actuellement développé par l'équipe R Development Core.
Le cœur de R est un langage informatique interprété qui permet le branchement et le bouclage ainsi que la programmation modulaire à l'aide de fonctions. R permet une intégration avec les procédures écrites dans les langages C, C ++, .Net, Python ou FORTRAN pour plus d'efficacité.
R est disponible gratuitement sous la licence publique générale GNU, et des versions binaires précompilées sont fournies pour divers systèmes d'exploitation tels que Linux, Windows et Mac.
R est un logiciel libre distribué sous une copie de style GNU à gauche, et une partie officielle du projet GNU appelée GNU S.
Évolution de R
R a été initialement écrit par Ross Ihaka et Robert Gentlemanau Département de statistique de l'Université d'Auckland à Auckland, Nouvelle-Zélande. R a fait sa première apparition en 1993.
Un grand groupe d'individus a contribué à R en envoyant du code et des rapports de bogues.
Depuis la mi-1997, il existe un groupe de base (la "R Core Team") qui peut modifier l'archive du code source R.
Caractéristiques de R
Comme indiqué précédemment, R est un langage de programmation et un environnement logiciel pour l'analyse statistique, la représentation graphique et le reporting. Voici les caractéristiques importantes de R -
R est un langage de programmation bien développé, simple et efficace qui comprend des conditions, des boucles, des fonctions récursives définies par l'utilisateur et des fonctions d'entrée et de sortie.
R dispose d'une installation efficace de traitement et de stockage des données,
R fournit une suite d'opérateurs pour les calculs sur des tableaux, des listes, des vecteurs et des matrices.
R fournit une vaste collection d'outils cohérents et intégrés pour l'analyse des données.
R fournit des fonctionnalités graphiques pour l'analyse des données et l'affichage soit directement sur l'ordinateur, soit pour l'impression sur les papiers.
En conclusion, R est le langage de programmation de statistiques le plus utilisé au monde. C'est le choix n ° 1 des data scientists et soutenu par une communauté dynamique et talentueuse de contributeurs. R est enseigné dans les universités et déployé dans des applications métier critiques. Ce tutoriel vous apprendra la programmation R avec des exemples appropriés en étapes simples et faciles.
Configuration de l'environnement local
Si vous souhaitez toujours configurer votre environnement pour R, vous pouvez suivre les étapes ci-dessous.
Installation de Windows
Vous pouvez télécharger la version du programme d'installation Windows de R à partir de R-3.2.2 pour Windows (32/64 bits) et l'enregistrer dans un répertoire local.
Comme il s'agit d'un programme d'installation Windows (.exe) avec un nom "R-version-win.exe". Vous pouvez simplement double-cliquer et exécuter le programme d'installation en acceptant les paramètres par défaut. Si votre Windows est une version 32 bits, il installe la version 32 bits. Mais si votre Windows est 64 bits, il installe les versions 32 bits et 64 bits.
Après l'installation, vous pouvez localiser l'icône pour exécuter le programme dans une structure de répertoires "R \ R3.2.2 \ bin \ i386 \ Rgui.exe" sous les fichiers de programme Windows. Cliquer sur cette icône fait apparaître la R-GUI qui est la console R pour effectuer la programmation R.
Installation sous Linux
R est disponible en tant que binaire pour de nombreuses versions de Linux à l'emplacement R Binaries .
Les instructions pour installer Linux varient d'une saveur à l'autre. Ces étapes sont mentionnées sous chaque type de version Linux dans le lien mentionné. Cependant, si vous êtes pressé, vous pouvez utiliseryum commande pour installer R comme suit -
$ yum install RLa commande ci-dessus installera les fonctionnalités de base de la programmation R avec les packages standard, vous avez toujours besoin d'un package supplémentaire, vous pouvez alors lancer l'invite R comme suit -
$ R
R version 3.2.0 (2015-04-16) -- "Full of Ingredients"
Copyright (C) 2015 The R Foundation for Statistical Computing
Platform: x86_64-redhat-linux-gnu (64-bit)
R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.
R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.
Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.
>Vous pouvez maintenant utiliser la commande d'installation à l'invite R pour installer le package requis. Par exemple, la commande suivante installeraplotrix package requis pour les graphiques 3D.
> install.packages("plotrix")Par convention, nous commencerons à apprendre la programmation R en écrivant un "Hello, World!" programme. Selon les besoins, vous pouvez programmer à l'invite de commande R ou vous pouvez utiliser un fichier de script R pour écrire votre programme. Vérifions les deux un par un.
Invite de commandes R
Une fois que vous avez configuré l'environnement R, il est facile de démarrer votre invite de commande R en tapant simplement la commande suivante à votre invite de commande -
$ RCela lancera l'interpréteur R et vous obtiendrez une invite> où vous pouvez commencer à taper votre programme comme suit -
> myString <- "Hello, World!"
> print ( myString)
[1] "Hello, World!"Ici, la première instruction définit une variable de chaîne myString, où nous attribuons une chaîne "Hello, World!" puis l'instruction suivante print () est utilisée pour imprimer la valeur stockée dans la variable myString.
Fichier de script R
Habituellement, vous ferez votre programmation en écrivant vos programmes dans des fichiers de script, puis vous exécuterez ces scripts à votre invite de commande à l'aide de l'interpréteur R appelé Rscript. Commençons donc par écrire le code suivant dans un fichier texte appelé test.R comme sous -
# My first program in R Programming
myString <- "Hello, World!"
print ( myString)Enregistrez le code ci-dessus dans un fichier test.R et exécutez-le à l'invite de commande Linux comme indiqué ci-dessous. Même si vous utilisez Windows ou un autre système, la syntaxe restera la même.
$ Rscript test.RLorsque nous exécutons le programme ci-dessus, il produit le résultat suivant.
[1] "Hello, World!"commentaires
Les commentaires sont comme un texte d'aide dans votre programme R et ils sont ignorés par l'interpréteur lors de l'exécution de votre programme réel. Un seul commentaire est écrit en utilisant # au début de l'instruction comme suit -
# My first program in R ProgrammingR ne prend pas en charge les commentaires sur plusieurs lignes, mais vous pouvez effectuer une astuce qui se présente comme suit -
if(FALSE) {
"This is a demo for multi-line comments and it should be put inside either a
single OR double quote"
}
myString <- "Hello, World!"
print ( myString)[1] "Hello, World!"Bien que les commentaires ci-dessus soient exécutés par l'interpréteur R, ils n'interféreront pas avec votre programme actuel. Vous devez mettre ces commentaires à l'intérieur, soit des guillemets simples, soit des guillemets doubles.
En général, lorsque vous programmez dans n'importe quel langage de programmation, vous devez utiliser diverses variables pour stocker diverses informations. Les variables ne sont rien d'autre que des emplacements de mémoire réservés pour stocker des valeurs. Cela signifie que, lorsque vous créez une variable, vous réservez de l'espace en mémoire.
Vous pouvez souhaiter stocker des informations de différents types de données comme des caractères, des caractères larges, des nombres entiers, des virgule flottante, des virgules flottantes doubles, des valeurs booléennes, etc. En fonction du type de données d'une variable, le système d'exploitation alloue de la mémoire et décide de ce qui peut être stocké dans le mémoire réservée.
Contrairement à d'autres langages de programmation comme C et java dans R, les variables ne sont pas déclarées comme un type de données. Les variables sont affectées avec des objets R et le type de données de l'objet R devient le type de données de la variable. Il existe de nombreux types d'objets R. Les plus fréquemment utilisés sont -
- Vectors
- Lists
- Matrices
- Arrays
- Factors
- Cadres de données
Le plus simple de ces objets est le vector objectet il existe six types de données de ces vecteurs atomiques, également appelés six classes de vecteurs. Les autres objets R sont construits sur les vecteurs atomiques.
| Type de données | Exemple | Vérifier |
|---|---|---|
| Logique | VRAI FAUX |
il produit le résultat suivant - |
| Numérique | 12,3, 5, 999 |
il produit le résultat suivant - |
| Entier | 2L, 34L, 0L |
il produit le résultat suivant - |
| Complexe | 3 + 2i |
il produit le résultat suivant - |
| Personnage | "a", "bon", "VRAI", "23,4" |
il produit le résultat suivant - |
| Brut | "Hello" est stocké sous 48 65 6c 6c 6f |
il produit le résultat suivant - |
Dans la programmation R, les types de données très basiques sont les objets R appelés vectorsqui contiennent des éléments de différentes classes comme indiqué ci-dessus. Veuillez noter que dans R, le nombre de classes n'est pas limité aux six types ci-dessus. Par exemple, nous pouvons utiliser de nombreux vecteurs atomiques et créer un tableau dont la classe deviendra tableau.
Vecteurs
Lorsque vous souhaitez créer un vecteur avec plus d'un élément, vous devez utiliser c() fonction qui signifie combiner les éléments en un vecteur.
# Create a vector.
apple <- c('red','green',"yellow")
print(apple)
# Get the class of the vector.
print(class(apple))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "red" "green" "yellow"
[1] "character"Listes
Une liste est un objet R qui peut contenir de nombreux types d'éléments différents à l'intérieur comme des vecteurs, des fonctions et même une autre liste à l'intérieur.
# Create a list.
list1 <- list(c(2,5,3),21.3,sin)
# Print the list.
print(list1)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[[1]]
[1] 2 5 3
[[2]]
[1] 21.3
[[3]]
function (x) .Primitive("sin")Matrices
Une matrice est un ensemble de données rectangulaire bidimensionnel. Il peut être créé à l'aide d'une entrée vectorielle dans la fonction de matrice.
# Create a matrix.
M = matrix( c('a','a','b','c','b','a'), nrow = 2, ncol = 3, byrow = TRUE)
print(M)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[,1] [,2] [,3]
[1,] "a" "a" "b"
[2,] "c" "b" "a"Tableaux
Alors que les matrices sont limitées à deux dimensions, les tableaux peuvent être de n'importe quel nombre de dimensions. La fonction de tableau prend un attribut dim qui crée le nombre requis de dimension. Dans l'exemple ci-dessous, nous créons un tableau avec deux éléments qui sont chacun des matrices 3x3.
# Create an array.
a <- array(c('green','yellow'),dim = c(3,3,2))
print(a)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
, , 1
[,1] [,2] [,3]
[1,] "green" "yellow" "green"
[2,] "yellow" "green" "yellow"
[3,] "green" "yellow" "green"
, , 2
[,1] [,2] [,3]
[1,] "yellow" "green" "yellow"
[2,] "green" "yellow" "green"
[3,] "yellow" "green" "yellow"Les facteurs
Les facteurs sont les r-objets créés à l'aide d'un vecteur. Il stocke le vecteur avec les valeurs distinctes des éléments du vecteur sous forme d'étiquettes. Les étiquettes sont toujours des caractères indépendamment du fait que ce soit numérique, caractère ou booléen, etc. dans le vecteur d'entrée. Ils sont utiles dans la modélisation statistique.
Les facteurs sont créés à l'aide du factor()fonction. lenlevels fonctions donne le nombre de niveaux.
# Create a vector.
apple_colors <- c('green','green','yellow','red','red','red','green')
# Create a factor object.
factor_apple <- factor(apple_colors)
# Print the factor.
print(factor_apple)
print(nlevels(factor_apple))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] green green yellow red red red green
Levels: green red yellow
[1] 3Cadres de données
Les blocs de données sont des objets de données tabulaires. Contrairement à une matrice dans un bloc de données, chaque colonne peut contenir différents modes de données. La première colonne peut être numérique tandis que la deuxième colonne peut être un caractère et la troisième colonne peut être logique. C'est une liste de vecteurs d'égale longueur.
Les trames de données sont créées à l'aide du data.frame() fonction.
# Create the data frame.
BMI <- data.frame(
gender = c("Male", "Male","Female"),
height = c(152, 171.5, 165),
weight = c(81,93, 78),
Age = c(42,38,26)
)
print(BMI)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
gender height weight Age
1 Male 152.0 81 42
2 Male 171.5 93 38
3 Female 165.0 78 26Une variable nous fournit un stockage nommé que nos programmes peuvent manipuler. Une variable dans R peut stocker un vecteur atomique, un groupe de vecteurs atomiques ou une combinaison de plusieurs Robjects. Un nom de variable valide se compose de lettres, de chiffres et de points ou de caractères de soulignement. Le nom de la variable commence par une lettre ou le point non suivi d'un chiffre.
| Nom de variable | Validité | Raison |
|---|---|---|
| nom_var2. | valide | Contient des lettres, des chiffres, des points et des traits de soulignement |
| var_name% | Invalide | A le caractère '%'. Seuls les points (.) Et les traits de soulignement sont autorisés. |
| 2var_name | invalide | Commence par un nombre |
.var_name, var.name |
valide | Peut commencer par un point (.) Mais le point (.) Ne doit pas être suivi d'un nombre. |
| .2nom_var | invalide | Le point de départ est suivi d'un nombre le rendant invalide. |
| _var_name | invalide | Commence par _ qui n'est pas valide |
Affectation de variable
Les variables peuvent recevoir des valeurs en utilisant l'opérateur vers la gauche, vers la droite et égal à. Les valeurs des variables peuvent être imprimées en utilisantprint() ou cat()fonction. lecat() La fonction combine plusieurs éléments en une sortie d'impression continue.
# Assignment using equal operator.
var.1 = c(0,1,2,3)
# Assignment using leftward operator.
var.2 <- c("learn","R")
# Assignment using rightward operator.
c(TRUE,1) -> var.3
print(var.1)
cat ("var.1 is ", var.1 ,"\n")
cat ("var.2 is ", var.2 ,"\n")
cat ("var.3 is ", var.3 ,"\n")Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 0 1 2 3
var.1 is 0 1 2 3
var.2 is learn R
var.3 is 1 1Note- Le vecteur c (TRUE, 1) a un mélange de classe logique et numérique. Ainsi, la classe logique est forcée à la classe numérique rendant TRUE comme 1.
Type de données d'une variable
Dans R, une variable elle-même n'est déclarée d'aucun type de données, elle obtient plutôt le type de données de l'objet R qui lui est assigné. Donc R est appelé un langage typé dynamiquement, ce qui signifie que nous pouvons changer le type de données d'une variable de la même variable encore et encore lors de son utilisation dans un programme.
var_x <- "Hello"
cat("The class of var_x is ",class(var_x),"\n")
var_x <- 34.5
cat(" Now the class of var_x is ",class(var_x),"\n")
var_x <- 27L
cat(" Next the class of var_x becomes ",class(var_x),"\n")Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
The class of var_x is character
Now the class of var_x is numeric
Next the class of var_x becomes integerRecherche de variables
Pour connaître toutes les variables actuellement disponibles dans l'espace de travail nous utilisons le ls()fonction. La fonction ls () peut également utiliser des modèles pour faire correspondre les noms de variables.
print(ls())Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "my var" "my_new_var" "my_var" "var.1"
[5] "var.2" "var.3" "var.name" "var_name2."
[9] "var_x" "varname"Note - Il s'agit d'un exemple de sortie en fonction des variables déclarées dans votre environnement.
La fonction ls () peut utiliser des modèles pour faire correspondre les noms de variables.
# List the variables starting with the pattern "var".
print(ls(pattern = "var"))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "my var" "my_new_var" "my_var" "var.1"
[5] "var.2" "var.3" "var.name" "var_name2."
[9] "var_x" "varname"Les variables commençant par dot(.) sont cachés, ils peuvent être listés en utilisant l'argument "all.names = TRUE" de la fonction ls ().
print(ls(all.name = TRUE))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] ".cars" ".Random.seed" ".var_name" ".varname" ".varname2"
[6] "my var" "my_new_var" "my_var" "var.1" "var.2"
[11]"var.3" "var.name" "var_name2." "var_x"Suppression de variables
Les variables peuvent être supprimées en utilisant le rm()fonction. Ci-dessous, nous supprimons la variable var.3. Lors de l'impression, la valeur de l'erreur variable est renvoyée.
rm(var.3)
print(var.3)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "var.3"
Error in print(var.3) : object 'var.3' not foundToutes les variables peuvent être supprimées en utilisant le rm() et ls() fonctionnent ensemble.
rm(list = ls())
print(ls())Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
character(0)Un opérateur est un symbole qui indique au compilateur d'effectuer des manipulations mathématiques ou logiques spécifiques. Le langage R est riche en opérateurs intégrés et fournit les types d'opérateurs suivants.
Types d'opérateurs
Nous avons les types d'opérateurs suivants dans la programmation R -
- Opérateurs arithmétiques
- Opérateurs relationnels
- Opérateurs logiques
- Opérateurs d'affectation
- Opérateurs divers
Opérateurs arithmétiques
Le tableau suivant montre les opérateurs arithmétiques pris en charge par le langage R. Les opérateurs agissent sur chaque élément du vecteur.
| Opérateur | La description | Exemple |
|---|---|---|
| + | Ajoute deux vecteurs |
il produit le résultat suivant - |
| - | Soustrait le deuxième vecteur du premier |
il produit le résultat suivant - |
| * | Multiplie les deux vecteurs |
il produit le résultat suivant - |
| / | Divisez le premier vecteur par le second |
Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant - |
| %% | Donnez le reste du premier vecteur avec le second |
il produit le résultat suivant - |
| % /% | Le résultat de la division du premier vecteur avec le second (quotient) |
il produit le résultat suivant - |
| ^ | Le premier vecteur élevé à l'exposant du deuxième vecteur |
il produit le résultat suivant - |
Opérateurs relationnels
Le tableau suivant montre les opérateurs relationnels pris en charge par le langage R. Chaque élément du premier vecteur est comparé à l'élément correspondant du deuxième vecteur. Le résultat de la comparaison est une valeur booléenne.
| Opérateur | La description | Exemple |
|---|---|---|
| > | Vérifie si chaque élément du premier vecteur est supérieur à l'élément correspondant du deuxième vecteur. |
il produit le résultat suivant - |
| < | Vérifie si chaque élément du premier vecteur est inférieur à l'élément correspondant du deuxième vecteur. |
il produit le résultat suivant - |
| == | Vérifie si chaque élément du premier vecteur est égal à l'élément correspondant du deuxième vecteur. |
il produit le résultat suivant - |
| <= | Vérifie si chaque élément du premier vecteur est inférieur ou égal à l'élément correspondant du deuxième vecteur. |
il produit le résultat suivant - |
| > = | Vérifie si chaque élément du premier vecteur est supérieur ou égal à l'élément correspondant du deuxième vecteur. |
il produit le résultat suivant - |
| ! = | Vérifie si chaque élément du premier vecteur est différent de l'élément correspondant du deuxième vecteur. |
il produit le résultat suivant - |
Opérateurs logiques
Le tableau suivant montre les opérateurs logiques pris en charge par le langage R. Elle n'est applicable qu'aux vecteurs de type logique, numérique ou complexe. Tous les nombres supérieurs à 1 sont considérés comme une valeur logique TRUE.
Chaque élément du premier vecteur est comparé à l'élément correspondant du deuxième vecteur. Le résultat de la comparaison est une valeur booléenne.
| Opérateur | La description | Exemple |
|---|---|---|
| & | Il est appelé opérateur ET logique par élément. Il combine chaque élément du premier vecteur avec l'élément correspondant du deuxième vecteur et donne une sortie TRUE si les deux éléments sont TRUE. |
il produit le résultat suivant - |
| | | Il est appelé opérateur OR logique par élément. Il combine chaque élément du premier vecteur avec l'élément correspondant du deuxième vecteur et donne une sortie TRUE si l'un des éléments est TRUE. |
il produit le résultat suivant - |
| ! | Il est appelé opérateur logique NON. Prend chaque élément du vecteur et donne la valeur logique opposée. |
il produit le résultat suivant - |
L'opérateur logique && et || considère uniquement le premier élément des vecteurs et donne un vecteur d'élément unique en sortie.
| Opérateur | La description | Exemple |
|---|---|---|
| && | Opérateur logique ET appelé. Prend le premier élément des deux vecteurs et donne le VRAI uniquement si les deux sont VRAI. |
il produit le résultat suivant - |
| || | Opérateur logique OU appelé. Prend le premier élément des deux vecteurs et donne VRAI si l'un d'eux est VRAI. |
il produit le résultat suivant - |
Opérateurs d'affectation
Ces opérateurs sont utilisés pour attribuer des valeurs aux vecteurs.
| Opérateur | La description | Exemple |
|---|---|---|
| <- ou = ou << - |
Affectation de gauche appelée |
il produit le résultat suivant - |
| -> ou - >> |
Affectation de droite appelée |
il produit le résultat suivant - |
Opérateurs divers
Ces opérateurs sont utilisés à des fins spécifiques et non pour des calculs mathématiques ou logiques généraux.
| Opérateur | La description | Exemple |
|---|---|---|
| : | Opérateur du colon. Il crée la série de nombres en séquence pour un vecteur. |
il produit le résultat suivant - |
| %dans% | Cet opérateur permet d'identifier si un élément appartient à un vecteur. |
il produit le résultat suivant - |
| % *% | Cet opérateur permet de multiplier une matrice avec sa transposée. |
il produit le résultat suivant - |
Les structures de prise de décision exigent que le programmeur spécifie une ou plusieurs conditions à évaluer ou à tester par le programme, ainsi qu'une ou plusieurs instructions à exécuter si la condition est déterminée comme étant true, et éventuellement d'autres instructions à exécuter si la condition est déterminée false.
Voici la forme générale d'une structure de prise de décision typique trouvée dans la plupart des langages de programmation -
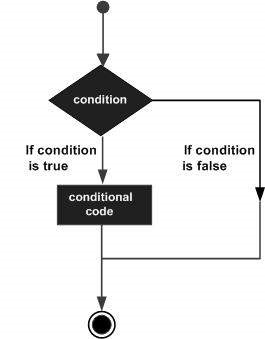
R fournit les types d'énoncés décisionnels suivants. Cliquez sur les liens suivants pour vérifier leurs détails.
| Sr.No. | Déclaration et description |
|---|---|
| 1 | si déclaration Un if instruction se compose d'une expression booléenne suivie d'une ou plusieurs instructions. |
| 2 | instruction if ... else Un if l'instruction peut être suivie d'une instruction facultative else instruction, qui s'exécute lorsque l'expression booléenne est fausse. |
| 3 | instruction switch UNE switch L'instruction permet à une variable d'être testée pour l'égalité par rapport à une liste de valeurs. |
Il peut arriver que vous deviez exécuter un bloc de code plusieurs fois. En général, les instructions sont exécutées de manière séquentielle. La première instruction d'une fonction est exécutée en premier, suivie de la seconde, et ainsi de suite.
Les langages de programmation fournissent diverses structures de contrôle qui permettent des chemins d'exécution plus compliqués.
Une instruction de boucle nous permet d'exécuter une instruction ou un groupe d'instructions plusieurs fois et ce qui suit est la forme générale d'une instruction de boucle dans la plupart des langages de programmation -
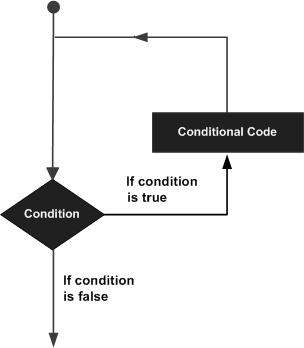
Le langage de programmation R fournit les types de boucle suivants pour gérer les exigences de bouclage. Cliquez sur les liens suivants pour vérifier leurs détails.
| Sr.No. | Type de boucle et description |
|---|---|
| 1 | boucle de répétition Exécute une séquence d'instructions plusieurs fois et abrége le code qui gère la variable de boucle. |
| 2 | boucle while Répète une instruction ou un groupe d'instructions tant qu'une condition donnée est vraie. Il teste la condition avant d'exécuter le corps de la boucle. |
| 3 | pour boucle Comme une instruction while, sauf qu'elle teste la condition à la fin du corps de la boucle. |
Déclarations de contrôle de boucle
Les instructions de contrôle de boucle modifient l'exécution de sa séquence normale. Lorsque l'exécution quitte une étendue, tous les objets automatiques qui ont été créés dans cette étendue sont détruits.
R prend en charge les instructions de contrôle suivantes. Cliquez sur les liens suivants pour vérifier leurs détails.
| Sr.No. | Déclaration de contrôle et description |
|---|---|
| 1 | déclaration break Met fin au loop et transfère l'exécution à l'instruction immédiatement après la boucle. |
| 2 | Prochaine déclaration le next L'instruction simule le comportement du commutateur R. |
Une fonction est un ensemble d'instructions organisées ensemble pour effectuer une tâche spécifique. R a un grand nombre de fonctions intégrées et l'utilisateur peut créer ses propres fonctions.
Dans R, une fonction est un objet, donc l'interpréteur R est capable de passer le contrôle à la fonction, ainsi que les arguments qui peuvent être nécessaires pour que la fonction accomplisse les actions.
La fonction effectue à son tour sa tâche et retourne le contrôle à l'interpréteur ainsi que tout résultat qui peut être stocké dans d'autres objets.
Définition de fonction
Une fonction R est créée à l'aide du mot-clé function. La syntaxe de base d'une définition de fonction R est la suivante -
function_name <- function(arg_1, arg_2, ...) {
Function body
}Composants fonctionnels
Les différentes parties d'une fonction sont -
Function Name- Ceci est le nom réel de la fonction. Il est stocké dans l'environnement R en tant qu'objet portant ce nom.
Arguments- Un argument est un espace réservé. Lorsqu'une fonction est appelée, vous transmettez une valeur à l'argument. Les arguments sont facultatifs; autrement dit, une fonction peut ne contenir aucun argument. Les arguments peuvent également avoir des valeurs par défaut.
Function Body - Le corps de la fonction contient une collection d'instructions qui définit ce que fait la fonction.
Return Value - La valeur de retour d'une fonction est la dernière expression du corps de la fonction à évaluer.
R a beaucoup in-builtfonctions qui peuvent être directement appelées dans le programme sans les définir au préalable. Nous pouvons également créer et utiliser nos propres fonctions appeléesuser defined les fonctions.
Fonction intégrée
Des exemples simples de fonctions intégrées sont seq(), mean(), max(), sum(x) et paste(...)etc. Ils sont directement appelés par les programmes écrits par l'utilisateur. Vous pouvez vous référer aux fonctions R les plus utilisées.
# Create a sequence of numbers from 32 to 44.
print(seq(32,44))
# Find mean of numbers from 25 to 82.
print(mean(25:82))
# Find sum of numbers frm 41 to 68.
print(sum(41:68))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 32 33 34 35 36 37 38 39 40 41 42 43 44
[1] 53.5
[1] 1526Fonction définie par l'utilisateur
Nous pouvons créer des fonctions définies par l'utilisateur dans R. Elles sont spécifiques à ce qu'un utilisateur souhaite et une fois créées, elles peuvent être utilisées comme les fonctions intégrées. Voici un exemple de la façon dont une fonction est créée et utilisée.
# Create a function to print squares of numbers in sequence.
new.function <- function(a) {
for(i in 1:a) {
b <- i^2
print(b)
}
}Appeler une fonction
# Create a function to print squares of numbers in sequence.
new.function <- function(a) {
for(i in 1:a) {
b <- i^2
print(b)
}
}
# Call the function new.function supplying 6 as an argument.
new.function(6)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 1
[1] 4
[1] 9
[1] 16
[1] 25
[1] 36Appel d'une fonction sans argument
# Create a function without an argument.
new.function <- function() {
for(i in 1:5) {
print(i^2)
}
}
# Call the function without supplying an argument.
new.function()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 1
[1] 4
[1] 9
[1] 16
[1] 25Appel d'une fonction avec des valeurs d'argument (par position et par nom)
Les arguments d'un appel de fonction peuvent être fournis dans la même séquence que celle définie dans la fonction ou ils peuvent être fournis dans une séquence différente, mais affectés aux noms des arguments.
# Create a function with arguments.
new.function <- function(a,b,c) {
result <- a * b + c
print(result)
}
# Call the function by position of arguments.
new.function(5,3,11)
# Call the function by names of the arguments.
new.function(a = 11, b = 5, c = 3)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 26
[1] 58Appel d'une fonction avec l'argument par défaut
Nous pouvons définir la valeur des arguments dans la définition de la fonction et appeler la fonction sans fournir d'argument pour obtenir le résultat par défaut. Mais nous pouvons également appeler de telles fonctions en fournissant de nouvelles valeurs de l'argument et obtenir un résultat non par défaut.
# Create a function with arguments.
new.function <- function(a = 3, b = 6) {
result <- a * b
print(result)
}
# Call the function without giving any argument.
new.function()
# Call the function with giving new values of the argument.
new.function(9,5)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 18
[1] 45Évaluation paresseuse de la fonction
Les arguments des fonctions sont évalués paresseusement, ce qui signifie qu'ils ne sont évalués que lorsque cela est nécessaire par le corps de la fonction.
# Create a function with arguments.
new.function <- function(a, b) {
print(a^2)
print(a)
print(b)
}
# Evaluate the function without supplying one of the arguments.
new.function(6)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 36
[1] 6
Error in print(b) : argument "b" is missing, with no defaultToute valeur écrite dans une paire de guillemets simples ou doubles dans R est traitée comme une chaîne. En interne, R stocke chaque chaîne entre guillemets, même lorsque vous les créez avec des guillemets simples.
Règles appliquées dans la construction de chaînes
Les guillemets au début et à la fin d'une chaîne doivent être à la fois des guillemets doubles ou des guillemets simples. Ils ne peuvent pas être mélangés.
Des guillemets doubles peuvent être insérés dans une chaîne commençant et se terminant par un guillemet simple.
Les guillemets simples peuvent être insérés dans une chaîne commençant et se terminant par des guillemets doubles.
Les guillemets doubles ne peuvent pas être insérés dans une chaîne commençant et se terminant par des guillemets doubles.
Le guillemet simple ne peut pas être inséré dans une chaîne commençant et se terminant par un guillemet simple.
Exemples de chaînes valides
Les exemples suivants clarifient les règles de création d'une chaîne dans R.
a <- 'Start and end with single quote'
print(a)
b <- "Start and end with double quotes"
print(b)
c <- "single quote ' in between double quotes"
print(c)
d <- 'Double quotes " in between single quote'
print(d)Lorsque le code ci-dessus est exécuté, nous obtenons la sortie suivante -
[1] "Start and end with single quote"
[1] "Start and end with double quotes"
[1] "single quote ' in between double quote"
[1] "Double quote \" in between single quote"Exemples de chaînes non valides
e <- 'Mixed quotes"
print(e)
f <- 'Single quote ' inside single quote'
print(f)
g <- "Double quotes " inside double quotes"
print(g)Lorsque nous exécutons le script, il ne donne pas les résultats ci-dessous.
Error: unexpected symbol in:
"print(e)
f <- 'Single"
Execution haltedManipulation de chaînes
Concaténation de chaînes - fonction paste ()
De nombreuses chaînes de R sont combinées à l'aide du paste()fonction. Il peut prendre n'importe quel nombre d'arguments pour être combinés.
Syntaxe
La syntaxe de base de la fonction coller est -
paste(..., sep = " ", collapse = NULL)Voici la description des paramètres utilisés -
... représente n'importe quel nombre d'arguments à combiner.
sepreprésente tout séparateur entre les arguments. C'est facultatif.
collapseest utilisé pour éliminer l'espace entre deux chaînes. Mais pas l'espace entre deux mots d'une chaîne.
Exemple
a <- "Hello"
b <- 'How'
c <- "are you? "
print(paste(a,b,c))
print(paste(a,b,c, sep = "-"))
print(paste(a,b,c, sep = "", collapse = ""))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "Hello How are you? "
[1] "Hello-How-are you? "
[1] "HelloHoware you? "Formatage des nombres et des chaînes - fonction format ()
Les nombres et les chaînes peuvent être formatés dans un style spécifique à l'aide de format() fonction.
Syntaxe
La syntaxe de base de la fonction de format est -
format(x, digits, nsmall, scientific, width, justify = c("left", "right", "centre", "none"))Voici la description des paramètres utilisés -
x est l'entrée vectorielle.
digits est le nombre total de chiffres affichés.
nsmall est le nombre minimum de chiffres à droite de la virgule décimale.
scientific est réglé sur TRUE pour afficher la notation scientifique.
width indique la largeur minimale à afficher en remplissant les blancs au début.
justify est l'affichage de la chaîne à gauche, à droite ou au centre.
Exemple
# Total number of digits displayed. Last digit rounded off.
result <- format(23.123456789, digits = 9)
print(result)
# Display numbers in scientific notation.
result <- format(c(6, 13.14521), scientific = TRUE)
print(result)
# The minimum number of digits to the right of the decimal point.
result <- format(23.47, nsmall = 5)
print(result)
# Format treats everything as a string.
result <- format(6)
print(result)
# Numbers are padded with blank in the beginning for width.
result <- format(13.7, width = 6)
print(result)
# Left justify strings.
result <- format("Hello", width = 8, justify = "l")
print(result)
# Justfy string with center.
result <- format("Hello", width = 8, justify = "c")
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "23.1234568"
[1] "6.000000e+00" "1.314521e+01"
[1] "23.47000"
[1] "6"
[1] " 13.7"
[1] "Hello "
[1] " Hello "Comptage du nombre de caractères dans une chaîne - fonction nchar ()
Cette fonction compte le nombre de caractères, espaces compris dans une chaîne.
Syntaxe
La syntaxe de base de la fonction nchar () est -
nchar(x)Voici la description des paramètres utilisés -
x est l'entrée vectorielle.
Exemple
result <- nchar("Count the number of characters")
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 30Changer la casse - fonctions toupper () et tolower ()
Ces fonctions modifient la casse des caractères d'une chaîne.
Syntaxe
La syntaxe de base de la fonction toupper () et tolower () est -
toupper(x)
tolower(x)Voici la description des paramètres utilisés -
x est l'entrée vectorielle.
Exemple
# Changing to Upper case.
result <- toupper("Changing To Upper")
print(result)
# Changing to lower case.
result <- tolower("Changing To Lower")
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "CHANGING TO UPPER"
[1] "changing to lower"Extraction de parties d'une chaîne - fonction substring ()
Cette fonction extrait des parties d'une chaîne.
Syntaxe
La syntaxe de base de la fonction substring () est -
substring(x,first,last)Voici la description des paramètres utilisés -
x est l'entrée du vecteur de caractères.
first est la position du premier caractère à extraire.
last est la position du dernier caractère à extraire.
Exemple
# Extract characters from 5th to 7th position.
result <- substring("Extract", 5, 7)
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "act"Les vecteurs sont les objets de données R les plus élémentaires et il existe six types de vecteurs atomiques. Ils sont logiques, entiers, doubles, complexes, de caractère et bruts.
Création de vecteur
Vecteur d'élément unique
Même lorsque vous n'écrivez qu'une seule valeur dans R, elle devient un vecteur de longueur 1 et appartient à l'un des types de vecteurs ci-dessus.
# Atomic vector of type character.
print("abc");
# Atomic vector of type double.
print(12.5)
# Atomic vector of type integer.
print(63L)
# Atomic vector of type logical.
print(TRUE)
# Atomic vector of type complex.
print(2+3i)
# Atomic vector of type raw.
print(charToRaw('hello'))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "abc"
[1] 12.5
[1] 63
[1] TRUE
[1] 2+3i
[1] 68 65 6c 6c 6fVecteur d'éléments multiples
Using colon operator with numeric data
# Creating a sequence from 5 to 13.
v <- 5:13
print(v)
# Creating a sequence from 6.6 to 12.6.
v <- 6.6:12.6
print(v)
# If the final element specified does not belong to the sequence then it is discarded.
v <- 3.8:11.4
print(v)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 5 6 7 8 9 10 11 12 13
[1] 6.6 7.6 8.6 9.6 10.6 11.6 12.6
[1] 3.8 4.8 5.8 6.8 7.8 8.8 9.8 10.8Using sequence (Seq.) operator
# Create vector with elements from 5 to 9 incrementing by 0.4.
print(seq(5, 9, by = 0.4))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 5.0 5.4 5.8 6.2 6.6 7.0 7.4 7.8 8.2 8.6 9.0Using the c() function
Les valeurs non-caractères sont forcées au type caractère si l'un des éléments est un caractère.
# The logical and numeric values are converted to characters.
s <- c('apple','red',5,TRUE)
print(s)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "apple" "red" "5" "TRUE"Accès aux éléments vectoriels
Les éléments d'un vecteur sont accessibles à l'aide de l'indexation. le[ ] bracketssont utilisés pour l'indexation. L'indexation commence par la position 1. Donner une valeur négative dans l'index supprime cet élément du résultat.TRUE, FALSE ou 0 et 1 peut également être utilisé pour l'indexation.
# Accessing vector elements using position.
t <- c("Sun","Mon","Tue","Wed","Thurs","Fri","Sat")
u <- t[c(2,3,6)]
print(u)
# Accessing vector elements using logical indexing.
v <- t[c(TRUE,FALSE,FALSE,FALSE,FALSE,TRUE,FALSE)]
print(v)
# Accessing vector elements using negative indexing.
x <- t[c(-2,-5)]
print(x)
# Accessing vector elements using 0/1 indexing.
y <- t[c(0,0,0,0,0,0,1)]
print(y)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "Mon" "Tue" "Fri"
[1] "Sun" "Fri"
[1] "Sun" "Tue" "Wed" "Fri" "Sat"
[1] "Sun"Manipulation vectorielle
Arithmétique vectorielle
Deux vecteurs de même longueur peuvent être ajoutés, soustraits, multipliés ou divisés, donnant le résultat comme une sortie vectorielle.
# Create two vectors.
v1 <- c(3,8,4,5,0,11)
v2 <- c(4,11,0,8,1,2)
# Vector addition.
add.result <- v1+v2
print(add.result)
# Vector subtraction.
sub.result <- v1-v2
print(sub.result)
# Vector multiplication.
multi.result <- v1*v2
print(multi.result)
# Vector division.
divi.result <- v1/v2
print(divi.result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 7 19 4 13 1 13
[1] -1 -3 4 -3 -1 9
[1] 12 88 0 40 0 22
[1] 0.7500000 0.7272727 Inf 0.6250000 0.0000000 5.5000000Recyclage des éléments vectoriels
Si nous appliquons des opérations arithmétiques à deux vecteurs de longueur inégale, alors les éléments du vecteur plus court sont recyclés pour terminer les opérations.
v1 <- c(3,8,4,5,0,11)
v2 <- c(4,11)
# V2 becomes c(4,11,4,11,4,11)
add.result <- v1+v2
print(add.result)
sub.result <- v1-v2
print(sub.result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 7 19 8 16 4 22
[1] -1 -3 0 -6 -4 0Tri des éléments vectoriels
Les éléments d'un vecteur peuvent être triés à l'aide de la sort() fonction.
v <- c(3,8,4,5,0,11, -9, 304)
# Sort the elements of the vector.
sort.result <- sort(v)
print(sort.result)
# Sort the elements in the reverse order.
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)
# Sorting character vectors.
v <- c("Red","Blue","yellow","violet")
sort.result <- sort(v)
print(sort.result)
# Sorting character vectors in reverse order.
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] -9 0 3 4 5 8 11 304
[1] 304 11 8 5 4 3 0 -9
[1] "Blue" "Red" "violet" "yellow"
[1] "yellow" "violet" "Red" "Blue"Les listes sont les objets R qui contiennent des éléments de différents types tels que des nombres, des chaînes, des vecteurs et une autre liste à l'intérieur. Une liste peut également contenir une matrice ou une fonction comme éléments. La liste est créée en utilisantlist() fonction.
Créer une liste
Voici un exemple pour créer une liste contenant des chaînes, des nombres, des vecteurs et des valeurs logiques.
# Create a list containing strings, numbers, vectors and a logical
# values.
list_data <- list("Red", "Green", c(21,32,11), TRUE, 51.23, 119.1)
print(list_data)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[[1]]
[1] "Red"
[[2]]
[1] "Green"
[[3]]
[1] 21 32 11
[[4]]
[1] TRUE
[[5]]
[1] 51.23
[[6]]
[1] 119.1Nommer les éléments de la liste
Les éléments de la liste peuvent être nommés et accessibles en utilisant ces noms.
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Show the list.
print(list_data)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
$`1st_Quarter` [1] "Jan" "Feb" "Mar" $A_Matrix
[,1] [,2] [,3]
[1,] 3 5 -2
[2,] 9 1 8
$A_Inner_list $A_Inner_list[[1]]
[1] "green"
$A_Inner_list[[2]]
[1] 12.3Accès aux éléments de liste
Les éléments de la liste sont accessibles par l'index de l'élément dans la liste. Dans le cas de listes nommées, il est également possible d'accéder à l'aide des noms.
Nous continuons à utiliser la liste dans l'exemple ci-dessus -
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Access the first element of the list.
print(list_data[1])
# Access the thrid element. As it is also a list, all its elements will be printed.
print(list_data[3])
# Access the list element using the name of the element.
print(list_data$A_Matrix)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
$`1st_Quarter` [1] "Jan" "Feb" "Mar" $A_Inner_list
$A_Inner_list[[1]] [1] "green" $A_Inner_list[[2]]
[1] 12.3
[,1] [,2] [,3]
[1,] 3 5 -2
[2,] 9 1 8Manipulation des éléments de liste
Nous pouvons ajouter, supprimer et mettre à jour des éléments de liste comme indiqué ci-dessous. Nous ne pouvons ajouter et supprimer des éléments qu'à la fin d'une liste. Mais nous pouvons mettre à jour n'importe quel élément.
# Create a list containing a vector, a matrix and a list.
list_data <- list(c("Jan","Feb","Mar"), matrix(c(3,9,5,1,-2,8), nrow = 2),
list("green",12.3))
# Give names to the elements in the list.
names(list_data) <- c("1st Quarter", "A_Matrix", "A Inner list")
# Add element at the end of the list.
list_data[4] <- "New element"
print(list_data[4])
# Remove the last element.
list_data[4] <- NULL
# Print the 4th Element.
print(list_data[4])
# Update the 3rd Element.
list_data[3] <- "updated element"
print(list_data[3])Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[[1]]
[1] "New element"
$<NA> NULL $`A Inner list`
[1] "updated element"Fusion de listes
Vous pouvez fusionner plusieurs listes en une seule liste en plaçant toutes les listes dans une fonction list ().
# Create two lists.
list1 <- list(1,2,3)
list2 <- list("Sun","Mon","Tue")
# Merge the two lists.
merged.list <- c(list1,list2)
# Print the merged list.
print(merged.list)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[[1]]
[1] 1
[[2]]
[1] 2
[[3]]
[1] 3
[[4]]
[1] "Sun"
[[5]]
[1] "Mon"
[[6]]
[1] "Tue"Conversion de liste en vecteur
Une liste peut être convertie en vecteur afin que les éléments du vecteur puissent être utilisés pour une manipulation ultérieure. Toutes les opérations arithmétiques sur les vecteurs peuvent être appliquées après la conversion de la liste en vecteurs. Pour effectuer cette conversion, nous utilisons leunlist()fonction. Il prend la liste comme entrée et produit un vecteur.
# Create lists.
list1 <- list(1:5)
print(list1)
list2 <-list(10:14)
print(list2)
# Convert the lists to vectors.
v1 <- unlist(list1)
v2 <- unlist(list2)
print(v1)
print(v2)
# Now add the vectors
result <- v1+v2
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[[1]]
[1] 1 2 3 4 5
[[1]]
[1] 10 11 12 13 14
[1] 1 2 3 4 5
[1] 10 11 12 13 14
[1] 11 13 15 17 19Les matrices sont les objets R dans lesquels les éléments sont disposés selon une disposition rectangulaire bidimensionnelle. Ils contiennent des éléments des mêmes types atomiques. Bien que nous puissions créer une matrice contenant uniquement des caractères ou uniquement des valeurs logiques, elles ne sont pas d'une grande utilité. Nous utilisons des matrices contenant des éléments numériques à utiliser dans les calculs mathématiques.
Une matrice est créée à l'aide du matrix() fonction.
Syntaxe
La syntaxe de base pour créer une matrice dans R est -
matrix(data, nrow, ncol, byrow, dimnames)Voici la description des paramètres utilisés -
data est le vecteur d'entrée qui devient les éléments de données de la matrice.
nrow est le nombre de lignes à créer.
ncol est le nombre de colonnes à créer.
byrowest un indice logique. Si TRUE, les éléments vectoriels d'entrée sont organisés par ligne.
dimname correspond aux noms attribués aux lignes et aux colonnes.
Exemple
Créez une matrice en prenant un vecteur de nombres en entrée.
# Elements are arranged sequentially by row.
M <- matrix(c(3:14), nrow = 4, byrow = TRUE)
print(M)
# Elements are arranged sequentially by column.
N <- matrix(c(3:14), nrow = 4, byrow = FALSE)
print(N)
# Define the column and row names.
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
print(P)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[,1] [,2] [,3]
[1,] 3 4 5
[2,] 6 7 8
[3,] 9 10 11
[4,] 12 13 14
[,1] [,2] [,3]
[1,] 3 7 11
[2,] 4 8 12
[3,] 5 9 13
[4,] 6 10 14
col1 col2 col3
row1 3 4 5
row2 6 7 8
row3 9 10 11
row4 12 13 14Accéder aux éléments d'une matrice
Les éléments d'une matrice sont accessibles en utilisant l'index de colonne et de ligne de l'élément. Nous considérons la matrice P ci-dessus pour trouver les éléments spécifiques ci-dessous.
# Define the column and row names.
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
# Create the matrix.
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
# Access the element at 3rd column and 1st row.
print(P[1,3])
# Access the element at 2nd column and 4th row.
print(P[4,2])
# Access only the 2nd row.
print(P[2,])
# Access only the 3rd column.
print(P[,3])Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 5
[1] 13
col1 col2 col3
6 7 8
row1 row2 row3 row4
5 8 11 14Calculs matriciels
Diverses opérations mathématiques sont effectuées sur les matrices à l'aide des opérateurs R. Le résultat de l'opération est également une matrice.
Les dimensions (nombre de lignes et de colonnes) doivent être les mêmes pour les matrices impliquées dans l'opération.
Addition et soustraction de matrice
# Create two 2x3 matrices.
matrix1 <- matrix(c(3, 9, -1, 4, 2, 6), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(5, 2, 0, 9, 3, 4), nrow = 2)
print(matrix2)
# Add the matrices.
result <- matrix1 + matrix2
cat("Result of addition","\n")
print(result)
# Subtract the matrices
result <- matrix1 - matrix2
cat("Result of subtraction","\n")
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[,1] [,2] [,3]
[1,] 3 -1 2
[2,] 9 4 6
[,1] [,2] [,3]
[1,] 5 0 3
[2,] 2 9 4
Result of addition
[,1] [,2] [,3]
[1,] 8 -1 5
[2,] 11 13 10
Result of subtraction
[,1] [,2] [,3]
[1,] -2 -1 -1
[2,] 7 -5 2Multiplication et division matricielles
# Create two 2x3 matrices.
matrix1 <- matrix(c(3, 9, -1, 4, 2, 6), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(5, 2, 0, 9, 3, 4), nrow = 2)
print(matrix2)
# Multiply the matrices.
result <- matrix1 * matrix2
cat("Result of multiplication","\n")
print(result)
# Divide the matrices
result <- matrix1 / matrix2
cat("Result of division","\n")
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[,1] [,2] [,3]
[1,] 3 -1 2
[2,] 9 4 6
[,1] [,2] [,3]
[1,] 5 0 3
[2,] 2 9 4
Result of multiplication
[,1] [,2] [,3]
[1,] 15 0 6
[2,] 18 36 24
Result of division
[,1] [,2] [,3]
[1,] 0.6 -Inf 0.6666667
[2,] 4.5 0.4444444 1.5000000Les tableaux sont les objets de données R qui peuvent stocker des données dans plus de deux dimensions. Par exemple - Si nous créons un tableau de dimension (2, 3, 4), il crée 4 matrices rectangulaires chacune avec 2 lignes et 3 colonnes. Les tableaux ne peuvent stocker que le type de données.
Un tableau est créé à l'aide du array()fonction. Il prend des vecteurs comme entrée et utilise les valeurs dudim paramètre pour créer un tableau.
Exemple
L'exemple suivant crée un tableau de deux matrices 3x3 avec chacune 3 lignes et 3 colonnes.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2))
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
, , 1
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
, , 2
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15Nommer les colonnes et les lignes
Nous pouvons donner des noms aux lignes, colonnes et matrices du tableau en utilisant le dimnames paramètre.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
column.names <- c("COL1","COL2","COL3")
row.names <- c("ROW1","ROW2","ROW3")
matrix.names <- c("Matrix1","Matrix2")
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2),dimnames = list(row.names,column.names,
matrix.names))
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
, , Matrix1
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15
, , Matrix2
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15Accès aux éléments de la baie
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
column.names <- c("COL1","COL2","COL3")
row.names <- c("ROW1","ROW2","ROW3")
matrix.names <- c("Matrix1","Matrix2")
# Take these vectors as input to the array.
result <- array(c(vector1,vector2),dim = c(3,3,2),dimnames = list(row.names,
column.names, matrix.names))
# Print the third row of the second matrix of the array.
print(result[3,,2])
# Print the element in the 1st row and 3rd column of the 1st matrix.
print(result[1,3,1])
# Print the 2nd Matrix.
print(result[,,2])Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
COL1 COL2 COL3
3 12 15
[1] 13
COL1 COL2 COL3
ROW1 5 10 13
ROW2 9 11 14
ROW3 3 12 15Manipulation des éléments de la matrice
Le tableau étant constitué de matrices à dimensions multiples, les opérations sur les éléments du tableau sont effectuées en accédant aux éléments des matrices.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
array1 <- array(c(vector1,vector2),dim = c(3,3,2))
# Create two vectors of different lengths.
vector3 <- c(9,1,0)
vector4 <- c(6,0,11,3,14,1,2,6,9)
array2 <- array(c(vector1,vector2),dim = c(3,3,2))
# create matrices from these arrays.
matrix1 <- array1[,,2]
matrix2 <- array2[,,2]
# Add the matrices.
result <- matrix1+matrix2
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[,1] [,2] [,3]
[1,] 10 20 26
[2,] 18 22 28
[3,] 6 24 30Calculs sur les éléments du tableau
Nous pouvons faire des calculs sur les éléments d'un tableau en utilisant le apply() fonction.
Syntaxe
apply(x, margin, fun)Voici la description des paramètres utilisés -
x est un tableau.
margin est le nom de l'ensemble de données utilisé.
fun est la fonction à appliquer sur les éléments du tableau.
Exemple
Nous utilisons la fonction apply () ci-dessous pour calculer la somme des éléments dans les lignes d'un tableau sur toutes les matrices.
# Create two vectors of different lengths.
vector1 <- c(5,9,3)
vector2 <- c(10,11,12,13,14,15)
# Take these vectors as input to the array.
new.array <- array(c(vector1,vector2),dim = c(3,3,2))
print(new.array)
# Use apply to calculate the sum of the rows across all the matrices.
result <- apply(new.array, c(1), sum)
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
, , 1
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
, , 2
[,1] [,2] [,3]
[1,] 5 10 13
[2,] 9 11 14
[3,] 3 12 15
[1] 56 68 60Les facteurs sont les objets de données qui sont utilisés pour catégoriser les données et les stocker sous forme de niveaux. Ils peuvent stocker à la fois des chaînes et des entiers. Ils sont utiles dans les colonnes qui ont un nombre limité de valeurs uniques. Comme «Homme», «Femme» et Vrai, Faux, etc. Ils sont utiles dans l'analyse des données pour la modélisation statistique.
Les facteurs sont créés à l'aide du factor () fonction en prenant un vecteur comme entrée.
Exemple
# Create a vector as input.
data <- c("East","West","East","North","North","East","West","West","West","East","North")
print(data)
print(is.factor(data))
# Apply the factor function.
factor_data <- factor(data)
print(factor_data)
print(is.factor(factor_data))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "East" "West" "East" "North" "North" "East" "West" "West" "West" "East" "North"
[1] FALSE
[1] East West East North North East West West West East North
Levels: East North West
[1] TRUEFacteurs dans la base de données
Lors de la création d'un bloc de données avec une colonne de données texte, R traite la colonne de texte comme des données catégorielles et crée des facteurs dessus.
# Create the vectors for data frame.
height <- c(132,151,162,139,166,147,122)
weight <- c(48,49,66,53,67,52,40)
gender <- c("male","male","female","female","male","female","male")
# Create the data frame.
input_data <- data.frame(height,weight,gender)
print(input_data)
# Test if the gender column is a factor.
print(is.factor(input_data$gender)) # Print the gender column so see the levels. print(input_data$gender)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
height weight gender
1 132 48 male
2 151 49 male
3 162 66 female
4 139 53 female
5 166 67 male
6 147 52 female
7 122 40 male
[1] TRUE
[1] male male female female male female male
Levels: female maleChanger l'ordre des niveaux
L'ordre des niveaux d'un facteur peut être modifié en appliquant à nouveau la fonction de facteur avec un nouvel ordre des niveaux.
data <- c("East","West","East","North","North","East","West",
"West","West","East","North")
# Create the factors
factor_data <- factor(data)
print(factor_data)
# Apply the factor function with required order of the level.
new_order_data <- factor(factor_data,levels = c("East","West","North"))
print(new_order_data)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] East West East North North East West West West East North
Levels: East North West
[1] East West East North North East West West West East North
Levels: East West NorthGénérer des niveaux de facteur
Nous pouvons générer des niveaux de facteur en utilisant le gl()fonction. Il prend deux entiers comme entrée qui indique combien de niveaux et combien de fois chaque niveau.
Syntaxe
gl(n, k, labels)Voici la description des paramètres utilisés -
n est un entier donnant le nombre de niveaux.
k est un entier donnant le nombre de réplications.
labels est un vecteur d'étiquettes pour les niveaux de facteurs résultants.
Exemple
v <- gl(3, 4, labels = c("Tampa", "Seattle","Boston"))
print(v)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Tampa Tampa Tampa Tampa Seattle Seattle Seattle Seattle Boston
[10] Boston Boston Boston
Levels: Tampa Seattle BostonUn bloc de données est une table ou une structure de type tableau bidimensionnelle dans laquelle chaque colonne contient les valeurs d'une variable et chaque ligne contient un ensemble de valeurs de chaque colonne.
Voici les caractéristiques d'une trame de données.
- Les noms de colonne doivent être non vides.
- Les noms de ligne doivent être uniques.
- Les données stockées dans un bloc de données peuvent être de type numérique, factoriel ou caractère.
- Chaque colonne doit contenir le même nombre d'éléments de données.
Créer un bloc de données
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Print the data frame.
print(emp.data)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
emp_id emp_name salary start_date
1 1 Rick 623.30 2012-01-01
2 2 Dan 515.20 2013-09-23
3 3 Michelle 611.00 2014-11-15
4 4 Ryan 729.00 2014-05-11
5 5 Gary 843.25 2015-03-27Obtenir la structure du bloc de données
La structure de la trame de données peut être vue en utilisant str() fonction.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Get the structure of the data frame.
str(emp.data)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
'data.frame': 5 obs. of 4 variables:
$ emp_id : int 1 2 3 4 5 $ emp_name : chr "Rick" "Dan" "Michelle" "Ryan" ...
$ salary : num 623 515 611 729 843 $ start_date: Date, format: "2012-01-01" "2013-09-23" "2014-11-15" "2014-05-11" ...Résumé des données dans la trame de données
Le résumé statistique et la nature des données peuvent être obtenus en appliquant summary() fonction.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Print the summary.
print(summary(emp.data))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
emp_id emp_name salary start_date
Min. :1 Length:5 Min. :515.2 Min. :2012-01-01
1st Qu.:2 Class :character 1st Qu.:611.0 1st Qu.:2013-09-23
Median :3 Mode :character Median :623.3 Median :2014-05-11
Mean :3 Mean :664.4 Mean :2014-01-14
3rd Qu.:4 3rd Qu.:729.0 3rd Qu.:2014-11-15
Max. :5 Max. :843.2 Max. :2015-03-27Extraire les données du bloc de données
Extraire une colonne spécifique d'un bloc de données à l'aide du nom de la colonne.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01","2013-09-23","2014-11-15","2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract Specific columns.
result <- data.frame(emp.data$emp_name,emp.data$salary)
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
emp.data.emp_name emp.data.salary
1 Rick 623.30
2 Dan 515.20
3 Michelle 611.00
4 Ryan 729.00
5 Gary 843.25Extraire les deux premières lignes, puis toutes les colonnes
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract first two rows.
result <- emp.data[1:2,]
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
emp_id emp_name salary start_date
1 1 Rick 623.3 2012-01-01
2 2 Dan 515.2 2013-09-23Extrait 3 ème et 5 ème ligne avec 2 ème et 4 ème colonne
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Extract 3rd and 5th row with 2nd and 4th column.
result <- emp.data[c(3,5),c(2,4)]
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
emp_name start_date
3 Michelle 2014-11-15
5 Gary 2015-03-27Développer le bloc de données
Un bloc de données peut être développé en ajoutant des colonnes et des lignes.
Ajouter une colonne
Ajoutez simplement le vecteur de colonne en utilisant un nouveau nom de colonne.
# Create the data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
stringsAsFactors = FALSE
)
# Add the "dept" coulmn.
emp.data$dept <- c("IT","Operations","IT","HR","Finance")
v <- emp.data
print(v)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
emp_id emp_name salary start_date dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 5 Gary 843.25 2015-03-27 FinanceAjouter une rangée
Pour ajouter plus de lignes de manière permanente à un bloc de données existant, nous devons insérer les nouvelles lignes dans la même structure que le bloc de données existant et utiliser le rbind() fonction.
Dans l'exemple ci-dessous, nous créons un bloc de données avec de nouvelles lignes et le fusionnons avec le bloc de données existant pour créer le bloc de données final.
# Create the first data frame.
emp.data <- data.frame(
emp_id = c (1:5),
emp_name = c("Rick","Dan","Michelle","Ryan","Gary"),
salary = c(623.3,515.2,611.0,729.0,843.25),
start_date = as.Date(c("2012-01-01", "2013-09-23", "2014-11-15", "2014-05-11",
"2015-03-27")),
dept = c("IT","Operations","IT","HR","Finance"),
stringsAsFactors = FALSE
)
# Create the second data frame
emp.newdata <- data.frame(
emp_id = c (6:8),
emp_name = c("Rasmi","Pranab","Tusar"),
salary = c(578.0,722.5,632.8),
start_date = as.Date(c("2013-05-21","2013-07-30","2014-06-17")),
dept = c("IT","Operations","Fianance"),
stringsAsFactors = FALSE
)
# Bind the two data frames.
emp.finaldata <- rbind(emp.data,emp.newdata)
print(emp.finaldata)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
emp_id emp_name salary start_date dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 5 Gary 843.25 2015-03-27 Finance
6 6 Rasmi 578.00 2013-05-21 IT
7 7 Pranab 722.50 2013-07-30 Operations
8 8 Tusar 632.80 2014-06-17 FiananceLes packages R sont une collection de fonctions R, de code conforme et d'exemples de données. Ils sont stockés dans un répertoire appelé"library"dans l'environnement R. Par défaut, R installe un ensemble de packages lors de l'installation. D'autres packages sont ajoutés plus tard, lorsqu'ils sont nécessaires à des fins spécifiques. Lorsque nous démarrons la console R, seuls les packages par défaut sont disponibles par défaut. Les autres packages déjà installés doivent être chargés explicitement pour être utilisés par le programme R qui va les utiliser.
Tous les packages disponibles en langage R sont répertoriés dans R Packages.
Vous trouverez ci-dessous une liste de commandes à utiliser pour vérifier, vérifier et utiliser les packages R.
Vérifier les packages R disponibles
Obtenir des emplacements de bibliothèque contenant des packages R
.libPaths()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant. Cela peut varier en fonction des paramètres locaux de votre ordinateur.
[2] "C:/Program Files/R/R-3.2.2/library"Obtenez la liste de tous les packages installés
library()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant. Cela peut varier en fonction des paramètres locaux de votre ordinateur.
Packages in library ‘C:/Program Files/R/R-3.2.2/library’:
base The R Base Package
boot Bootstrap Functions (Originally by Angelo Canty
for S)
class Functions for Classification
cluster "Finding Groups in Data": Cluster Analysis
Extended Rousseeuw et al.
codetools Code Analysis Tools for R
compiler The R Compiler Package
datasets The R Datasets Package
foreign Read Data Stored by 'Minitab', 'S', 'SAS',
'SPSS', 'Stata', 'Systat', 'Weka', 'dBase', ...
graphics The R Graphics Package
grDevices The R Graphics Devices and Support for Colours
and Fonts
grid The Grid Graphics Package
KernSmooth Functions for Kernel Smoothing Supporting Wand
& Jones (1995)
lattice Trellis Graphics for R
MASS Support Functions and Datasets for Venables and
Ripley's MASS
Matrix Sparse and Dense Matrix Classes and Methods
methods Formal Methods and Classes
mgcv Mixed GAM Computation Vehicle with GCV/AIC/REML
Smoothness Estimation
nlme Linear and Nonlinear Mixed Effects Models
nnet Feed-Forward Neural Networks and Multinomial
Log-Linear Models
parallel Support for Parallel computation in R
rpart Recursive Partitioning and Regression Trees
spatial Functions for Kriging and Point Pattern
Analysis
splines Regression Spline Functions and Classes
stats The R Stats Package
stats4 Statistical Functions using S4 Classes
survival Survival Analysis
tcltk Tcl/Tk Interface
tools Tools for Package Development
utils The R Utils PackageRécupère tous les packages actuellement chargés dans l'environnement R
search()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant. Cela peut varier en fonction des paramètres locaux de votre ordinateur.
[1] ".GlobalEnv" "package:stats" "package:graphics"
[4] "package:grDevices" "package:utils" "package:datasets"
[7] "package:methods" "Autoloads" "package:base"Installer un nouveau package
Il existe deux façons d'ajouter de nouveaux packages R. L'une consiste à installer directement à partir du répertoire CRAN et une autre à télécharger le package sur votre système local et à l'installer manuellement.
Installer directement depuis CRAN
La commande suivante récupère les packages directement à partir de la page Web CRAN et installe le package dans l'environnement R. Vous serez peut-être invité à choisir le miroir le plus proche. Choisissez celui qui convient à votre emplacement.
install.packages("Package Name")
# Install the package named "XML".
install.packages("XML")Installer le package manuellement
Allez sur le lien R Packages pour télécharger le package nécessaire. Enregistrez le package en tant que.zip fichier dans un emplacement approprié dans le système local.
Vous pouvez maintenant exécuter la commande suivante pour installer ce package dans l'environnement R.
install.packages(file_name_with_path, repos = NULL, type = "source")
# Install the package named "XML"
install.packages("E:/XML_3.98-1.3.zip", repos = NULL, type = "source")Charger le package dans la bibliothèque
Avant qu'un package puisse être utilisé dans le code, il doit être chargé dans l'environnement R actuel. Vous devez également charger un package qui est déjà installé précédemment mais qui n'est pas disponible dans l'environnement actuel.
Un package est chargé à l'aide de la commande suivante -
library("package Name", lib.loc = "path to library")
# Load the package named "XML"
install.packages("E:/XML_3.98-1.3.zip", repos = NULL, type = "source")Le remodelage des données dans R consiste à changer la façon dont les données sont organisées en lignes et en colonnes. La plupart du temps, le traitement des données dans R est effectué en prenant les données d'entrée comme une trame de données. Il est facile d'extraire des données des lignes et des colonnes d'une trame de données, mais il y a des situations où nous avons besoin de la trame de données dans un format différent de celui dans lequel nous l'avons reçue. R a de nombreuses fonctions pour diviser, fusionner et changer les lignes en colonnes et vice-versa dans un bloc de données.
Joindre des colonnes et des lignes dans un bloc de données
Nous pouvons joindre plusieurs vecteurs pour créer un bloc de données en utilisant le cbind()fonction. Nous pouvons également fusionner deux trames de données en utilisantrbind() fonction.
# Create vector objects.
city <- c("Tampa","Seattle","Hartford","Denver")
state <- c("FL","WA","CT","CO")
zipcode <- c(33602,98104,06161,80294)
# Combine above three vectors into one data frame.
addresses <- cbind(city,state,zipcode)
# Print a header.
cat("# # # # The First data frame\n")
# Print the data frame.
print(addresses)
# Create another data frame with similar columns
new.address <- data.frame(
city = c("Lowry","Charlotte"),
state = c("CO","FL"),
zipcode = c("80230","33949"),
stringsAsFactors = FALSE
)
# Print a header.
cat("# # # The Second data frame\n")
# Print the data frame.
print(new.address)
# Combine rows form both the data frames.
all.addresses <- rbind(addresses,new.address)
# Print a header.
cat("# # # The combined data frame\n")
# Print the result.
print(all.addresses)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
# # # # The First data frame
city state zipcode
[1,] "Tampa" "FL" "33602"
[2,] "Seattle" "WA" "98104"
[3,] "Hartford" "CT" "6161"
[4,] "Denver" "CO" "80294"
# # # The Second data frame
city state zipcode
1 Lowry CO 80230
2 Charlotte FL 33949
# # # The combined data frame
city state zipcode
1 Tampa FL 33602
2 Seattle WA 98104
3 Hartford CT 6161
4 Denver CO 80294
5 Lowry CO 80230
6 Charlotte FL 33949Fusion de trames de données
Nous pouvons fusionner deux trames de données en utilisant le merge()fonction. Les blocs de données doivent avoir les mêmes noms de colonne sur lesquels la fusion se produit.
Dans l'exemple ci-dessous, nous considérons les ensembles de données sur le diabète chez les femmes indiennes Pima disponibles dans les noms de bibliothèque "MASS". nous fusionnons les deux ensembles de données en fonction des valeurs de la pression artérielle («pb») et de l'indice de masse corporelle («bmi»). Lors du choix de ces deux colonnes pour la fusion, les enregistrements dans lesquels les valeurs de ces deux variables correspondent dans les deux ensembles de données sont combinés pour former une seule trame de données.
library(MASS)
merged.Pima <- merge(x = Pima.te, y = Pima.tr,
by.x = c("bp", "bmi"),
by.y = c("bp", "bmi")
)
print(merged.Pima)
nrow(merged.Pima)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
bp bmi npreg.x glu.x skin.x ped.x age.x type.x npreg.y glu.y skin.y ped.y
1 60 33.8 1 117 23 0.466 27 No 2 125 20 0.088
2 64 29.7 2 75 24 0.370 33 No 2 100 23 0.368
3 64 31.2 5 189 33 0.583 29 Yes 3 158 13 0.295
4 64 33.2 4 117 27 0.230 24 No 1 96 27 0.289
5 66 38.1 3 115 39 0.150 28 No 1 114 36 0.289
6 68 38.5 2 100 25 0.324 26 No 7 129 49 0.439
7 70 27.4 1 116 28 0.204 21 No 0 124 20 0.254
8 70 33.1 4 91 32 0.446 22 No 9 123 44 0.374
9 70 35.4 9 124 33 0.282 34 No 6 134 23 0.542
10 72 25.6 1 157 21 0.123 24 No 4 99 17 0.294
11 72 37.7 5 95 33 0.370 27 No 6 103 32 0.324
12 74 25.9 9 134 33 0.460 81 No 8 126 38 0.162
13 74 25.9 1 95 21 0.673 36 No 8 126 38 0.162
14 78 27.6 5 88 30 0.258 37 No 6 125 31 0.565
15 78 27.6 10 122 31 0.512 45 No 6 125 31 0.565
16 78 39.4 2 112 50 0.175 24 No 4 112 40 0.236
17 88 34.5 1 117 24 0.403 40 Yes 4 127 11 0.598
age.y type.y
1 31 No
2 21 No
3 24 No
4 21 No
5 21 No
6 43 Yes
7 36 Yes
8 40 No
9 29 Yes
10 28 No
11 55 No
12 39 No
13 39 No
14 49 Yes
15 49 Yes
16 38 No
17 28 No
[1] 17Fusion et coulée
L'un des aspects les plus intéressants de la programmation R consiste à changer la forme des données en plusieurs étapes pour obtenir la forme souhaitée. Les fonctions utilisées pour ce faire sont appeléesmelt() et cast().
Nous considérons l'ensemble de données appelé navires présent dans la bibliothèque appelée "MASS".
library(MASS)
print(ships)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
type year period service incidents
1 A 60 60 127 0
2 A 60 75 63 0
3 A 65 60 1095 3
4 A 65 75 1095 4
5 A 70 60 1512 6
.............
.............
8 A 75 75 2244 11
9 B 60 60 44882 39
10 B 60 75 17176 29
11 B 65 60 28609 58
............
............
17 C 60 60 1179 1
18 C 60 75 552 1
19 C 65 60 781 0
............
............Faire fondre les données
Maintenant, nous fondons les données pour les organiser, en convertissant toutes les colonnes autres que le type et l'année en plusieurs lignes.
molten.ships <- melt(ships, id = c("type","year"))
print(molten.ships)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
type year variable value
1 A 60 period 60
2 A 60 period 75
3 A 65 period 60
4 A 65 period 75
............
............
9 B 60 period 60
10 B 60 period 75
11 B 65 period 60
12 B 65 period 75
13 B 70 period 60
...........
...........
41 A 60 service 127
42 A 60 service 63
43 A 65 service 1095
...........
...........
70 D 70 service 1208
71 D 75 service 0
72 D 75 service 2051
73 E 60 service 45
74 E 60 service 0
75 E 65 service 789
...........
...........
101 C 70 incidents 6
102 C 70 incidents 2
103 C 75 incidents 0
104 C 75 incidents 1
105 D 60 incidents 0
106 D 60 incidents 0
...........
...........Lancer les données fondues
Nous pouvons convertir les données en fusion sous une nouvelle forme où l'agrégat de chaque type de navire pour chaque année est créé. Cela se fait en utilisant lecast() fonction.
recasted.ship <- cast(molten.ships, type+year~variable,sum)
print(recasted.ship)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
type year period service incidents
1 A 60 135 190 0
2 A 65 135 2190 7
3 A 70 135 4865 24
4 A 75 135 2244 11
5 B 60 135 62058 68
6 B 65 135 48979 111
7 B 70 135 20163 56
8 B 75 135 7117 18
9 C 60 135 1731 2
10 C 65 135 1457 1
11 C 70 135 2731 8
12 C 75 135 274 1
13 D 60 135 356 0
14 D 65 135 480 0
15 D 70 135 1557 13
16 D 75 135 2051 4
17 E 60 135 45 0
18 E 65 135 1226 14
19 E 70 135 3318 17
20 E 75 135 542 1Dans R, nous pouvons lire des données à partir de fichiers stockés en dehors de l'environnement R. Nous pouvons également écrire des données dans des fichiers qui seront stockés et accessibles par le système d'exploitation. R peut lire et écrire dans divers formats de fichiers tels que csv, excel, xml, etc.
Dans ce chapitre, nous allons apprendre à lire les données d'un fichier csv, puis à écrire des données dans un fichier csv. Le fichier doit être présent dans le répertoire de travail courant pour que R puisse le lire. Bien sûr, nous pouvons également définir notre propre répertoire et lire les fichiers à partir de là.
Obtention et configuration du répertoire de travail
Vous pouvez vérifier le répertoire vers lequel pointe l'espace de travail R à l'aide du getwd()fonction. Vous pouvez également définir un nouveau répertoire de travail en utilisantsetwd()fonction.
# Get and print current working directory.
print(getwd())
# Set current working directory.
setwd("/web/com")
# Get and print current working directory.
print(getwd())Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "/web/com/1441086124_2016"
[1] "/web/com"Ce résultat dépend de votre système d'exploitation et de votre répertoire actuel dans lequel vous travaillez.
Entrée sous forme de fichier CSV
Le fichier csv est un fichier texte dans lequel les valeurs des colonnes sont séparées par une virgule. Considérons les données suivantes présentes dans le fichier nomméinput.csv.
Vous pouvez créer ce fichier à l'aide du bloc-notes Windows en copiant et en collant ces données. Enregistrez le fichier sousinput.csv en utilisant l'option Enregistrer sous tous les fichiers (*. *) dans le bloc-notes.
id,name,salary,start_date,dept
1,Rick,623.3,2012-01-01,IT
2,Dan,515.2,2013-09-23,Operations
3,Michelle,611,2014-11-15,IT
4,Ryan,729,2014-05-11,HR
5,Gary,843.25,2015-03-27,Finance
6,Nina,578,2013-05-21,IT
7,Simon,632.8,2013-07-30,Operations
8,Guru,722.5,2014-06-17,FinanceLire un fichier CSV
Voici un exemple simple de read.csv() fonction pour lire un fichier CSV disponible dans votre répertoire de travail actuel -
data <- read.csv("input.csv")
print(data)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceAnalyse du fichier CSV
Par défaut, le read.csv()La fonction donne la sortie sous forme de trame de données. Cela peut être facilement vérifié comme suit. Nous pouvons également vérifier le nombre de colonnes et de lignes.
data <- read.csv("input.csv")
print(is.data.frame(data))
print(ncol(data))
print(nrow(data))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] TRUE
[1] 5
[1] 8Une fois que nous lisons les données dans une trame de données, nous pouvons appliquer toutes les fonctions applicables aux trames de données comme expliqué dans la section suivante.
Obtenez le salaire maximum
# Create a data frame.
data <- read.csv("input.csv")
# Get the max salary from data frame.
sal <- max(data$salary)
print(sal)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 843.25Obtenez les détails de la personne avec le salaire maximum
Nous pouvons récupérer des lignes répondant à des critères de filtre spécifiques similaires à une clause WHERE SQL.
# Create a data frame.
data <- read.csv("input.csv")
# Get the max salary from data frame.
sal <- max(data$salary)
# Get the person detail having max salary.
retval <- subset(data, salary == max(salary))
print(retval)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
id name salary start_date dept
5 NA Gary 843.25 2015-03-27 FinanceObtenez toutes les personnes travaillant dans le service informatique
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset( data, dept == "IT")
print(retval)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
id name salary start_date dept
1 1 Rick 623.3 2012-01-01 IT
3 3 Michelle 611.0 2014-11-15 IT
6 6 Nina 578.0 2013-05-21 ITObtenir les personnes du service informatique dont le salaire est supérieur à 600
# Create a data frame.
data <- read.csv("input.csv")
info <- subset(data, salary > 600 & dept == "IT")
print(info)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
id name salary start_date dept
1 1 Rick 623.3 2012-01-01 IT
3 3 Michelle 611.0 2014-11-15 ITObtenez les personnes qui ont rejoint en 2014 ou après
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
print(retval)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
id name salary start_date dept
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
8 8 Guru 722.50 2014-06-17 FinanceÉcriture dans un fichier CSV
R peut créer un fichier csv à partir d'une trame de données existante. lewrite.csv()La fonction est utilisée pour créer le fichier csv. Ce fichier est créé dans le répertoire de travail.
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
# Write filtered data into a new file.
write.csv(retval,"output.csv")
newdata <- read.csv("output.csv")
print(newdata)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
X id name salary start_date dept
1 3 3 Michelle 611.00 2014-11-15 IT
2 4 4 Ryan 729.00 2014-05-11 HR
3 5 NA Gary 843.25 2015-03-27 Finance
4 8 8 Guru 722.50 2014-06-17 FinanceIci, la colonne X provient du jeu de données newper. Cela peut être supprimé en utilisant des paramètres supplémentaires lors de l'écriture du fichier.
# Create a data frame.
data <- read.csv("input.csv")
retval <- subset(data, as.Date(start_date) > as.Date("2014-01-01"))
# Write filtered data into a new file.
write.csv(retval,"output.csv", row.names = FALSE)
newdata <- read.csv("output.csv")
print(newdata)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
id name salary start_date dept
1 3 Michelle 611.00 2014-11-15 IT
2 4 Ryan 729.00 2014-05-11 HR
3 NA Gary 843.25 2015-03-27 Finance
4 8 Guru 722.50 2014-06-17 FinanceMicrosoft Excel est le tableur le plus utilisé qui stocke les données au format .xls ou .xlsx. R peut lire directement à partir de ces fichiers à l'aide de certains packages spécifiques à Excel. Peu de tels paquets sont - XLConnect, xlsx, gdata etc. Nous utiliserons le paquet xlsx. R peut également écrire dans un fichier Excel en utilisant ce package.
Installer le package xlsx
Vous pouvez utiliser la commande suivante dans la console R pour installer le package «xlsx». Il peut demander l'installation de certains packages supplémentaires dont ce package dépend. Suivez la même commande avec le nom de package requis pour installer les packages supplémentaires.
install.packages("xlsx")Vérifier et charger le package «xlsx»
Utilisez la commande suivante pour vérifier et charger le package «xlsx».
# Verify the package is installed.
any(grepl("xlsx",installed.packages()))
# Load the library into R workspace.
library("xlsx")Lorsque le script est exécuté, nous obtenons la sortie suivante.
[1] TRUE
Loading required package: rJava
Loading required package: methods
Loading required package: xlsxjarsEntrée en tant que fichier xlsx
Ouvrez Microsoft Excel. Copiez et collez les données suivantes dans la feuille de travail nommée feuille1.
id name salary start_date dept
1 Rick 623.3 1/1/2012 IT
2 Dan 515.2 9/23/2013 Operations
3 Michelle 611 11/15/2014 IT
4 Ryan 729 5/11/2014 HR
5 Gary 43.25 3/27/2015 Finance
6 Nina 578 5/21/2013 IT
7 Simon 632.8 7/30/2013 Operations
8 Guru 722.5 6/17/2014 FinanceCopiez et collez également les données suivantes dans une autre feuille de calcul et renommez cette feuille de calcul en «ville».
name city
Rick Seattle
Dan Tampa
Michelle Chicago
Ryan Seattle
Gary Houston
Nina Boston
Simon Mumbai
Guru DallasEnregistrez le fichier Excel sous "input.xlsx". Vous devez l'enregistrer dans le répertoire de travail actuel de l'espace de travail R.
Lire le fichier Excel
Le fichier input.xlsx est lu en utilisant le read.xlsx()fonction comme indiqué ci-dessous. Le résultat est stocké sous forme de trame de données dans l'environnement R.
# Read the first worksheet in the file input.xlsx.
data <- read.xlsx("input.xlsx", sheetIndex = 1)
print(data)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceUn fichier binaire est un fichier qui contient des informations stockées uniquement sous forme de bits et d'octets (0 et 1). Ils ne sont pas lisibles par l'homme car les octets qu'ils contiennent se traduisent en caractères et symboles contenant de nombreux autres caractères non imprimables. Tenter de lire un fichier binaire à l'aide de n'importe quel éditeur de texte affichera des caractères comme Ø et ð.
Le fichier binaire doit être lu par des programmes spécifiques pour être utilisable. Par exemple, le fichier binaire d'un programme Microsoft Word peut être lu sous une forme lisible par l'homme uniquement par le programme Word. Ce qui indique qu'en plus du texte lisible par l'homme, il y a beaucoup plus d'informations comme le formatage des caractères et des numéros de page, etc., qui sont également stockés avec des caractères alphanumériques. Et enfin, un fichier binaire est une séquence continue d'octets. Le saut de ligne que nous voyons dans un fichier texte est un caractère joignant la première ligne à la suivante.
Parfois, les données générées par d'autres programmes doivent être traitées par R en tant que fichier binaire. R est également nécessaire pour créer des fichiers binaires qui peuvent être partagés avec d'autres programmes.
R a deux fonctions WriteBin() et readBin() pour créer et lire des fichiers binaires.
Syntaxe
writeBin(object, con)
readBin(con, what, n )Voici la description des paramètres utilisés -
con est l'objet de connexion pour lire ou écrire le fichier binaire.
object est le fichier binaire à écrire.
what est le mode tel que caractère, entier, etc. représentant les octets à lire.
n est le nombre d'octets à lire dans le fichier binaire.
Exemple
Nous considérons les données intégrées R "mtcars". Nous créons d'abord un fichier csv à partir de celui-ci et le convertissons en fichier binaire et le stockons en tant que fichier OS. Ensuite, nous lisons ce fichier binaire créé dans R.
Ecrire le fichier binaire
Nous lisons la trame de données "mtcars" sous forme de fichier csv, puis l'écrivons sous forme de fichier binaire dans le système d'exploitation.
# Read the "mtcars" data frame as a csv file and store only the columns
"cyl", "am" and "gear".
write.table(mtcars, file = "mtcars.csv",row.names = FALSE, na = "",
col.names = TRUE, sep = ",")
# Store 5 records from the csv file as a new data frame.
new.mtcars <- read.table("mtcars.csv",sep = ",",header = TRUE,nrows = 5)
# Create a connection object to write the binary file using mode "wb".
write.filename = file("/web/com/binmtcars.dat", "wb")
# Write the column names of the data frame to the connection object.
writeBin(colnames(new.mtcars), write.filename)
# Write the records in each of the column to the file.
writeBin(c(new.mtcars$cyl,new.mtcars$am,new.mtcars$gear), write.filename)
# Close the file for writing so that it can be read by other program.
close(write.filename)Lire le fichier binaire
Le fichier binaire créé ci-dessus stocke toutes les données sous forme d'octets continus. Nous allons donc le lire en choisissant les valeurs appropriées des noms de colonne ainsi que les valeurs de colonne.
# Create a connection object to read the file in binary mode using "rb".
read.filename <- file("/web/com/binmtcars.dat", "rb")
# First read the column names. n = 3 as we have 3 columns.
column.names <- readBin(read.filename, character(), n = 3)
# Next read the column values. n = 18 as we have 3 column names and 15 values.
read.filename <- file("/web/com/binmtcars.dat", "rb")
bindata <- readBin(read.filename, integer(), n = 18)
# Print the data.
print(bindata)
# Read the values from 4th byte to 8th byte which represents "cyl".
cyldata = bindata[4:8]
print(cyldata)
# Read the values form 9th byte to 13th byte which represents "am".
amdata = bindata[9:13]
print(amdata)
# Read the values form 9th byte to 13th byte which represents "gear".
geardata = bindata[14:18]
print(geardata)
# Combine all the read values to a dat frame.
finaldata = cbind(cyldata, amdata, geardata)
colnames(finaldata) = column.names
print(finaldata)Lorsque nous exécutons le code ci-dessus, il produit le résultat et le graphique suivants -
[1] 7108963 1728081249 7496037 6 6 4
[7] 6 8 1 1 1 0
[13] 0 4 4 4 3 3
[1] 6 6 4 6 8
[1] 1 1 1 0 0
[1] 4 4 4 3 3
cyl am gear
[1,] 6 1 4
[2,] 6 1 4
[3,] 4 1 4
[4,] 6 0 3
[5,] 8 0 3Comme nous pouvons le voir, nous avons récupéré les données d'origine en lisant le fichier binaire dans R.
XML est un format de fichier qui partage à la fois le format de fichier et les données sur le World Wide Web, les intranets et ailleurs en utilisant du texte ASCII standard. Il signifie Extensible Markup Language (XML). Semblable au HTML, il contient des balises de balisage. Mais contrairement au HTML où la balise de balisage décrit la structure de la page, en xml les balises de balisage décrivent la signification des données contenues dans le fichier.
Vous pouvez lire un fichier xml dans R en utilisant le package "XML". Ce package peut être installé à l'aide de la commande suivante.
install.packages("XML")Des données d'entrée
Créez un fichier XMl en copiant les données ci-dessous dans un éditeur de texte comme le bloc-notes. Enregistrez le fichier avec un.xml extension et en choisissant le type de fichier comme all files(*.*).
<RECORDS>
<EMPLOYEE>
<ID>1</ID>
<NAME>Rick</NAME>
<SALARY>623.3</SALARY>
<STARTDATE>1/1/2012</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>2</ID>
<NAME>Dan</NAME>
<SALARY>515.2</SALARY>
<STARTDATE>9/23/2013</STARTDATE>
<DEPT>Operations</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>3</ID>
<NAME>Michelle</NAME>
<SALARY>611</SALARY>
<STARTDATE>11/15/2014</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>4</ID>
<NAME>Ryan</NAME>
<SALARY>729</SALARY>
<STARTDATE>5/11/2014</STARTDATE>
<DEPT>HR</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>5</ID>
<NAME>Gary</NAME>
<SALARY>843.25</SALARY>
<STARTDATE>3/27/2015</STARTDATE>
<DEPT>Finance</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>6</ID>
<NAME>Nina</NAME>
<SALARY>578</SALARY>
<STARTDATE>5/21/2013</STARTDATE>
<DEPT>IT</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>7</ID>
<NAME>Simon</NAME>
<SALARY>632.8</SALARY>
<STARTDATE>7/30/2013</STARTDATE>
<DEPT>Operations</DEPT>
</EMPLOYEE>
<EMPLOYEE>
<ID>8</ID>
<NAME>Guru</NAME>
<SALARY>722.5</SALARY>
<STARTDATE>6/17/2014</STARTDATE>
<DEPT>Finance</DEPT>
</EMPLOYEE>
</RECORDS>Lire un fichier XML
Le fichier xml est lu par R à l'aide de la fonction xmlParse(). Il est stocké sous forme de liste dans R.
# Load the package required to read XML files.
library("XML")
# Also load the other required package.
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Print the result.
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
1
Rick
623.3
1/1/2012
IT
2
Dan
515.2
9/23/2013
Operations
3
Michelle
611
11/15/2014
IT
4
Ryan
729
5/11/2014
HR
5
Gary
843.25
3/27/2015
Finance
6
Nina
578
5/21/2013
IT
7
Simon
632.8
7/30/2013
Operations
8
Guru
722.5
6/17/2014
FinanceObtenir le nombre de nœuds présents dans un fichier XML
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Find number of nodes in the root.
rootsize <- xmlSize(rootnode)
# Print the result.
print(rootsize)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
output
[1] 8Détails du premier nœud
Regardons le premier enregistrement du fichier analysé. Cela nous donnera une idée des différents éléments présents dans le nœud de niveau supérieur.
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Print the result.
print(rootnode[1])Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
$EMPLOYEE
1
Rick
623.3
1/1/2012
IT
attr(,"class")
[1] "XMLInternalNodeList" "XMLNodeList"Obtenir différents éléments d'un nœud
# Load the packages required to read XML files.
library("XML")
library("methods")
# Give the input file name to the function.
result <- xmlParse(file = "input.xml")
# Exract the root node form the xml file.
rootnode <- xmlRoot(result)
# Get the first element of the first node.
print(rootnode[[1]][[1]])
# Get the fifth element of the first node.
print(rootnode[[1]][[5]])
# Get the second element of the third node.
print(rootnode[[3]][[2]])Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
1
IT
MichelleXML vers trame de données
Pour gérer efficacement les données dans des fichiers volumineux, nous lisons les données du fichier xml en tant que bloc de données. Traitez ensuite la trame de données pour l'analyse des données.
# Load the packages required to read XML files.
library("XML")
library("methods")
# Convert the input xml file to a data frame.
xmldataframe <- xmlToDataFrame("input.xml")
print(xmldataframe)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
ID NAME SALARY STARTDATE DEPT
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceComme les données sont maintenant disponibles sous forme de trame de données, nous pouvons utiliser la fonction liée à la trame de données pour lire et manipuler le fichier.
Le fichier JSON stocke les données sous forme de texte dans un format lisible par l'homme. Json signifie JavaScript Object Notation. R peut lire les fichiers JSON à l'aide du package rjson.
Installer le package rjson
Dans la console R, vous pouvez émettre la commande suivante pour installer le package rjson.
install.packages("rjson")Des données d'entrée
Créez un fichier JSON en copiant les données ci-dessous dans un éditeur de texte comme le bloc-notes. Enregistrez le fichier avec un.json extension et en choisissant le type de fichier comme all files(*.*).
{
"ID":["1","2","3","4","5","6","7","8" ],
"Name":["Rick","Dan","Michelle","Ryan","Gary","Nina","Simon","Guru" ],
"Salary":["623.3","515.2","611","729","843.25","578","632.8","722.5" ],
"StartDate":[ "1/1/2012","9/23/2013","11/15/2014","5/11/2014","3/27/2015","5/21/2013",
"7/30/2013","6/17/2014"],
"Dept":[ "IT","Operations","IT","HR","Finance","IT","Operations","Finance"]
}Lire le fichier JSON
Le fichier JSON est lu par R à l'aide de la fonction de JSON(). Il est stocké sous forme de liste dans R.
# Load the package required to read JSON files.
library("rjson")
# Give the input file name to the function.
result <- fromJSON(file = "input.json")
# Print the result.
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
$ID
[1] "1" "2" "3" "4" "5" "6" "7" "8"
$Name [1] "Rick" "Dan" "Michelle" "Ryan" "Gary" "Nina" "Simon" "Guru" $Salary
[1] "623.3" "515.2" "611" "729" "843.25" "578" "632.8" "722.5"
$StartDate [1] "1/1/2012" "9/23/2013" "11/15/2014" "5/11/2014" "3/27/2015" "5/21/2013" "7/30/2013" "6/17/2014" $Dept
[1] "IT" "Operations" "IT" "HR" "Finance" "IT"
"Operations" "Finance"Convertir JSON en un bloc de données
Nous pouvons convertir les données extraites ci-dessus en une trame de données R pour une analyse plus approfondie en utilisant le as.data.frame() fonction.
# Load the package required to read JSON files.
library("rjson")
# Give the input file name to the function.
result <- fromJSON(file = "input.json")
# Convert JSON file to a data frame.
json_data_frame <- as.data.frame(result)
print(json_data_frame)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
id, name, salary, start_date, dept
1 1 Rick 623.30 2012-01-01 IT
2 2 Dan 515.20 2013-09-23 Operations
3 3 Michelle 611.00 2014-11-15 IT
4 4 Ryan 729.00 2014-05-11 HR
5 NA Gary 843.25 2015-03-27 Finance
6 6 Nina 578.00 2013-05-21 IT
7 7 Simon 632.80 2013-07-30 Operations
8 8 Guru 722.50 2014-06-17 FinanceDe nombreux sites Web fournissent des données destinées à la consommation de leurs utilisateurs. Par exemple, l'Organisation mondiale de la santé (OMS) fournit des rapports sur la santé et les informations médicales sous forme de fichiers CSV, txt et XML. En utilisant les programmes R, nous pouvons extraire par programmation des données spécifiques de ces sites Web. Certains packages dans R qui sont utilisés pour supprimer des données du Web sont - "RCurl", XML "et" stringr ". Ils sont utilisés pour se connecter aux URL, identifier les liens requis pour les fichiers et les télécharger dans l'environnement local.
Installer les packages R
Les packages suivants sont nécessaires pour traiter les URL et les liens vers les fichiers. S'ils ne sont pas disponibles dans votre environnement R, vous pouvez les installer à l'aide des commandes suivantes.
install.packages("RCurl")
install.packages("XML")
install.packages("stringr")
install.packages("plyr")Des données d'entrée
Nous visiterons les données météorologiques URL et téléchargerons les fichiers CSV en utilisant R pour l'année 2015.
Exemple
Nous utiliserons la fonction getHTMLLinks()pour rassembler les URL des fichiers. Ensuite, nous utiliserons la fonctiondownload.file()pour enregistrer les fichiers sur le système local. Comme nous appliquerons le même code encore et encore pour plusieurs fichiers, nous allons créer une fonction à appeler plusieurs fois. Les noms de fichiers sont transmis en tant que paramètres sous la forme d'un objet de liste R à cette fonction.
# Read the URL.
url <- "http://www.geos.ed.ac.uk/~weather/jcmb_ws/"
# Gather the html links present in the webpage.
links <- getHTMLLinks(url)
# Identify only the links which point to the JCMB 2015 files.
filenames <- links[str_detect(links, "JCMB_2015")]
# Store the file names as a list.
filenames_list <- as.list(filenames)
# Create a function to download the files by passing the URL and filename list.
downloadcsv <- function (mainurl,filename) {
filedetails <- str_c(mainurl,filename)
download.file(filedetails,filename)
}
# Now apply the l_ply function and save the files into the current R working directory.
l_ply(filenames,downloadcsv,mainurl = "http://www.geos.ed.ac.uk/~weather/jcmb_ws/")Vérifier le téléchargement du fichier
Après avoir exécuté le code ci-dessus, vous pouvez localiser les fichiers suivants dans le répertoire de travail R actuel.
"JCMB_2015.csv" "JCMB_2015_Apr.csv" "JCMB_2015_Feb.csv" "JCMB_2015_Jan.csv"
"JCMB_2015_Mar.csv"Les données sont les systèmes de bases de données relationnelles sont stockées dans un format normalisé. Ainsi, pour effectuer des calculs statistiques, nous aurons besoin de requêtes SQL très avancées et complexes. Mais R peut se connecter facilement à de nombreuses bases de données relationnelles comme MySql, Oracle, serveur SQL, etc. et en extraire des enregistrements sous forme de trame de données. Une fois que les données sont disponibles dans l'environnement R, elles deviennent un ensemble de données R normal et peuvent être manipulées ou analysées à l'aide de tous les packages et fonctions puissants.
Dans ce tutoriel, nous utiliserons MySql comme base de données de référence pour la connexion à R.
Package RMySQL
R a un package intégré nommé "RMySQL" qui fournit une connectivité native entre avec la base de données MySql. Vous pouvez installer ce package dans l'environnement R à l'aide de la commande suivante.
install.packages("RMySQL")Connexion de R à MySql
Une fois le package installé, nous créons un objet de connexion dans R pour se connecter à la base de données. Il prend le nom d'utilisateur, le mot de passe, le nom de la base de données et le nom d'hôte comme entrée.
# Create a connection Object to MySQL database.
# We will connect to the sampel database named "sakila" that comes with MySql installation.
mysqlconnection = dbConnect(MySQL(), user = 'root', password = '', dbname = 'sakila',
host = 'localhost')
# List the tables available in this database.
dbListTables(mysqlconnection)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] "actor" "actor_info"
[3] "address" "category"
[5] "city" "country"
[7] "customer" "customer_list"
[9] "film" "film_actor"
[11] "film_category" "film_list"
[13] "film_text" "inventory"
[15] "language" "nicer_but_slower_film_list"
[17] "payment" "rental"
[19] "sales_by_film_category" "sales_by_store"
[21] "staff" "staff_list"
[23] "store"Interroger les tables
Nous pouvons interroger les tables de la base de données dans MySql en utilisant la fonction dbSendQuery(). La requête est exécutée dans MySql et le jeu de résultats est renvoyé à l'aide du Rfetch()fonction. Enfin, il est stocké sous forme de trame de données dans R.
# Query the "actor" tables to get all the rows.
result = dbSendQuery(mysqlconnection, "select * from actor")
# Store the result in a R data frame object. n = 5 is used to fetch first 5 rows.
data.frame = fetch(result, n = 5)
print(data.fame)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
actor_id first_name last_name last_update
1 1 PENELOPE GUINESS 2006-02-15 04:34:33
2 2 NICK WAHLBERG 2006-02-15 04:34:33
3 3 ED CHASE 2006-02-15 04:34:33
4 4 JENNIFER DAVIS 2006-02-15 04:34:33
5 5 JOHNNY LOLLOBRIGIDA 2006-02-15 04:34:33Requête avec clause de filtre
Nous pouvons passer n'importe quelle requête de sélection valide pour obtenir le résultat.
result = dbSendQuery(mysqlconnection, "select * from actor where last_name = 'TORN'")
# Fetch all the records(with n = -1) and store it as a data frame.
data.frame = fetch(result, n = -1)
print(data)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
actor_id first_name last_name last_update
1 18 DAN TORN 2006-02-15 04:34:33
2 94 KENNETH TORN 2006-02-15 04:34:33
3 102 WALTER TORN 2006-02-15 04:34:33Mise à jour des lignes dans les tables
Nous pouvons mettre à jour les lignes d'une table Mysql en passant la requête de mise à jour à la fonction dbSendQuery ().
dbSendQuery(mysqlconnection, "update mtcars set disp = 168.5 where hp = 110")Après avoir exécuté le code ci-dessus, nous pouvons voir le tableau mis à jour dans l'environnement MySql.
Insertion de données dans les tableaux
dbSendQuery(mysqlconnection,
"insert into mtcars(row_names, mpg, cyl, disp, hp, drat, wt, qsec, vs, am, gear, carb)
values('New Mazda RX4 Wag', 21, 6, 168.5, 110, 3.9, 2.875, 17.02, 0, 1, 4, 4)"
)Après avoir exécuté le code ci-dessus, nous pouvons voir la ligne insérée dans la table dans l'environnement MySql.
Création de tables dans MySql
Nous pouvons créer des tables dans MySql en utilisant la fonction dbWriteTable(). Il écrase la table si elle existe déjà et prend une trame de données en entrée.
# Create the connection object to the database where we want to create the table.
mysqlconnection = dbConnect(MySQL(), user = 'root', password = '', dbname = 'sakila',
host = 'localhost')
# Use the R data frame "mtcars" to create the table in MySql.
# All the rows of mtcars are taken inot MySql.
dbWriteTable(mysqlconnection, "mtcars", mtcars[, ], overwrite = TRUE)Après avoir exécuté le code ci-dessus, nous pouvons voir la table créée dans l'environnement MySql.
Suppression de tables dans MySql
Nous pouvons supprimer les tables de la base de données MySql en passant l'instruction drop table dans dbSendQuery () de la même manière que nous l'avons utilisée pour interroger les données des tables.
dbSendQuery(mysqlconnection, 'drop table if exists mtcars')Après avoir exécuté le code ci-dessus, nous pouvons voir que la table est supprimée dans l'environnement MySql.
Le langage de programmation R dispose de nombreuses bibliothèques pour créer des graphiques et des graphiques. Un camembert est une représentation des valeurs sous forme de tranches d'un cercle de différentes couleurs. Les tranches sont étiquetées et les nombres correspondant à chaque tranche sont également représentés dans le graphique.
Dans R, le graphique à secteurs est créé en utilisant le pie()fonction qui prend des nombres positifs comme entrée vectorielle. Les paramètres supplémentaires sont utilisés pour contrôler les étiquettes, la couleur, le titre, etc.
Syntaxe
La syntaxe de base pour créer un camembert à l'aide du R est -
pie(x, labels, radius, main, col, clockwise)Voici la description des paramètres utilisés -
x est un vecteur contenant les valeurs numériques utilisées dans le graphique à secteurs.
labels est utilisé pour donner une description aux tranches.
radius indique le rayon du cercle du camembert (valeur comprise entre -1 et +1).
main indique le titre du graphique.
col indique la palette de couleurs.
clockwise est une valeur logique indiquant si les tranches sont dessinées dans le sens horaire ou anti-horaire.
Exemple
Un camembert très simple est créé en utilisant uniquement le vecteur d'entrée et les étiquettes. Le script ci-dessous créera et enregistrera le graphique à secteurs dans le répertoire de travail R actuel.
# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")
# Give the chart file a name.
png(file = "city.png")
# Plot the chart.
pie(x,labels)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Titre et couleurs du graphique à secteurs
Nous pouvons étendre les fonctionnalités du graphique en ajoutant plus de paramètres à la fonction. Nous utiliserons le paramètremain pour ajouter un titre au graphique et un autre paramètre est colqui utilisera la palette de couleurs arc-en-ciel lors du dessin du graphique. La longueur de la palette doit être identique au nombre de valeurs que nous avons pour le graphique. Nous utilisons donc length (x).
Exemple
Le script ci-dessous créera et enregistrera le graphique à secteurs dans le répertoire de travail R actuel.
# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")
# Give the chart file a name.
png(file = "city_title_colours.jpg")
# Plot the chart with title and rainbow color pallet.
pie(x, labels, main = "City pie chart", col = rainbow(length(x)))
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Pourcentages de tranche et légende du graphique
Nous pouvons ajouter un pourcentage de tranche et une légende de graphique en créant des variables de graphique supplémentaires.
# Create data for the graph.
x <- c(21, 62, 10,53)
labels <- c("London","New York","Singapore","Mumbai")
piepercent<- round(100*x/sum(x), 1)
# Give the chart file a name.
png(file = "city_percentage_legends.jpg")
# Plot the chart.
pie(x, labels = piepercent, main = "City pie chart",col = rainbow(length(x)))
legend("topright", c("London","New York","Singapore","Mumbai"), cex = 0.8,
fill = rainbow(length(x)))
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
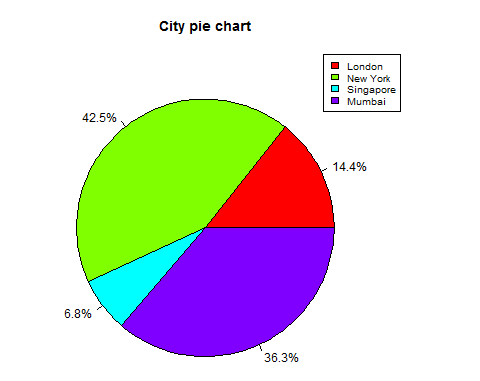
Graphique à secteurs 3D
Un graphique à secteurs avec 3 dimensions peut être dessiné à l'aide de packages supplémentaires. Le paquetplotrix a une fonction appelée pie3D() qui est utilisé pour cela.
# Get the library.
library(plotrix)
# Create data for the graph.
x <- c(21, 62, 10,53)
lbl <- c("London","New York","Singapore","Mumbai")
# Give the chart file a name.
png(file = "3d_pie_chart.jpg")
# Plot the chart.
pie3D(x,labels = lbl,explode = 0.1, main = "Pie Chart of Countries ")
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Un graphique à barres représente les données dans des barres rectangulaires dont la longueur de la barre est proportionnelle à la valeur de la variable. R utilise la fonctionbarplot()pour créer des graphiques à barres. R peut dessiner des barres verticales et horizontales dans le graphique à barres. Dans le diagramme à barres, chacune des barres peut avoir des couleurs différentes.
Syntaxe
La syntaxe de base pour créer un histogramme dans R est -
barplot(H,xlab,ylab,main, names.arg,col)Voici la description des paramètres utilisés -
- H est un vecteur ou une matrice contenant des valeurs numériques utilisées dans un graphique à barres.
- xlab est l'étiquette de l'axe x.
- ylab est l'étiquette de l'axe y.
- main est le titre du graphique à barres.
- names.arg est un vecteur de noms apparaissant sous chaque barre.
- col est utilisé pour donner des couleurs aux barres du graphique.
Exemple
Un graphique à barres simple est créé en utilisant uniquement le vecteur d'entrée et le nom de chaque barre.
Le script ci-dessous créera et enregistrera le graphique à barres dans le répertoire de travail R actuel.
# Create the data for the chart
H <- c(7,12,28,3,41)
# Give the chart file a name
png(file = "barchart.png")
# Plot the bar chart
barplot(H)
# Save the file
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Étiquettes, titre et couleurs des graphiques à barres
Les fonctionnalités du graphique à barres peuvent être développées en ajoutant plus de paramètres. lemain paramètre est utilisé pour ajouter title. lecolLe paramètre est utilisé pour ajouter des couleurs aux barres. leargs.name est un vecteur ayant le même nombre de valeurs que le vecteur d'entrée pour décrire la signification de chaque barre.
Exemple
Le script ci-dessous créera et enregistrera le graphique à barres dans le répertoire de travail R actuel.
# Create the data for the chart
H <- c(7,12,28,3,41)
M <- c("Mar","Apr","May","Jun","Jul")
# Give the chart file a name
png(file = "barchart_months_revenue.png")
# Plot the bar chart
barplot(H,names.arg=M,xlab="Month",ylab="Revenue",col="blue",
main="Revenue chart",border="red")
# Save the file
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
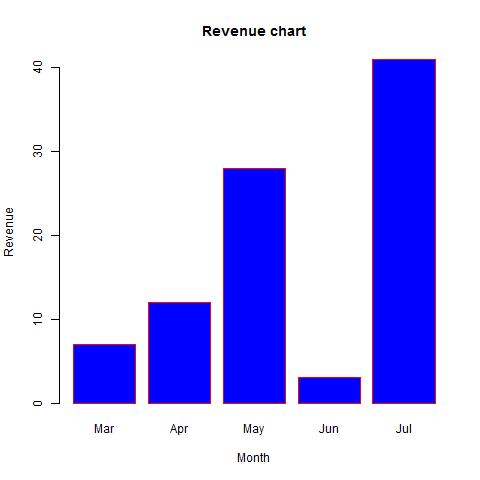
Diagramme à barres de groupe et diagramme à barres empilées
Nous pouvons créer un graphique à barres avec des groupes de barres et de piles dans chaque barre en utilisant une matrice comme valeurs d'entrée.
Plus de deux variables sont représentées sous forme de matrice utilisée pour créer le graphique à barres de groupe et le graphique à barres empilées.
# Create the input vectors.
colors = c("green","orange","brown")
months <- c("Mar","Apr","May","Jun","Jul")
regions <- c("East","West","North")
# Create the matrix of the values.
Values <- matrix(c(2,9,3,11,9,4,8,7,3,12,5,2,8,10,11), nrow = 3, ncol = 5, byrow = TRUE)
# Give the chart file a name
png(file = "barchart_stacked.png")
# Create the bar chart
barplot(Values, main = "total revenue", names.arg = months, xlab = "month", ylab = "revenue", col = colors)
# Add the legend to the chart
legend("topleft", regions, cex = 1.3, fill = colors)
# Save the file
dev.off()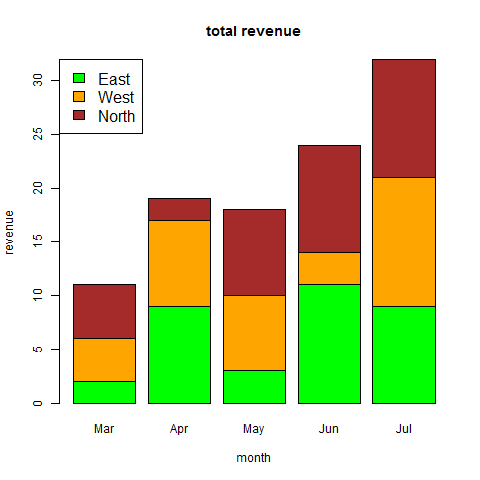
Les boîtes à moustaches mesurent la qualité de la distribution des données dans un ensemble de données. Il divise l'ensemble de données en trois quartiles. Ce graphique représente le minimum, le maximum, la médiane, le premier quartile et le troisième quartile de l'ensemble de données. Il est également utile de comparer la distribution des données entre les ensembles de données en dessinant des boîtes à moustaches pour chacun d'eux.
Les boîtes à moustaches sont créées dans R en utilisant le boxplot() fonction.
Syntaxe
La syntaxe de base pour créer un boxplot dans R est -
boxplot(x, data, notch, varwidth, names, main)Voici la description des paramètres utilisés -
x est un vecteur ou une formule.
data est la trame de données.
notchest une valeur logique. Définissez comme TRUE pour dessiner une encoche.
varwidthest une valeur logique. Définissez comme vrai pour dessiner la largeur de la boîte proportionnelle à la taille de l'échantillon.
names sont les étiquettes de groupe qui seront imprimées sous chaque boîte à moustaches.
main est utilisé pour donner un titre au graphique.
Exemple
Nous utilisons l'ensemble de données "mtcars" disponible dans l'environnement R pour créer un boxplot de base. Regardons les colonnes "mpg" et "cyl" dans mtcars.
input <- mtcars[,c('mpg','cyl')]
print(head(input))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
mpg cyl
Mazda RX4 21.0 6
Mazda RX4 Wag 21.0 6
Datsun 710 22.8 4
Hornet 4 Drive 21.4 6
Hornet Sportabout 18.7 8
Valiant 18.1 6Création du Boxplot
Le script ci-dessous créera une boîte à moustaches pour la relation entre mpg (miles par gallon) et cyl (nombre de cylindres).
# Give the chart file a name.
png(file = "boxplot.png")
# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars, xlab = "Number of Cylinders",
ylab = "Miles Per Gallon", main = "Mileage Data")
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
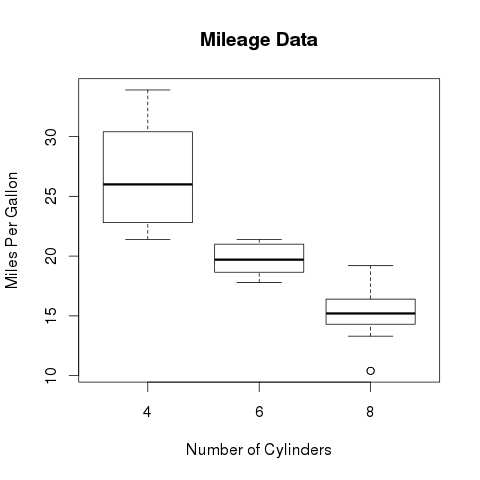
Boxplot avec Notch
Nous pouvons dessiner un boxplot avec encoche pour savoir comment les médianes des différents groupes de données correspondent les unes aux autres.
Le script ci-dessous créera un graphique boxplot avec une encoche pour chacun des groupes de données.
# Give the chart file a name.
png(file = "boxplot_with_notch.png")
# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars,
xlab = "Number of Cylinders",
ylab = "Miles Per Gallon",
main = "Mileage Data",
notch = TRUE,
varwidth = TRUE,
col = c("green","yellow","purple"),
names = c("High","Medium","Low")
)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
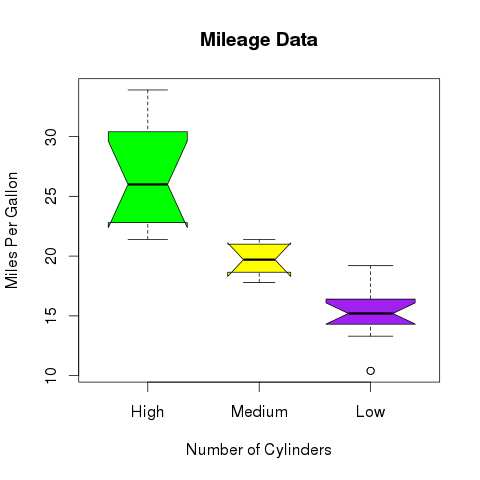
Un histogramme représente les fréquences des valeurs d'une variable regroupées en plages. L'histogramme est similaire au bar chat, mais la différence est qu'il regroupe les valeurs en plages continues. Chaque barre de l'histogramme représente la hauteur du nombre de valeurs présentes dans cette plage.
R crée un histogramme en utilisant hist()fonction. Cette fonction prend un vecteur comme entrée et utilise d'autres paramètres pour tracer des histogrammes.
Syntaxe
La syntaxe de base pour créer un histogramme à l'aide de R est -
hist(v,main,xlab,xlim,ylim,breaks,col,border)Voici la description des paramètres utilisés -
v est un vecteur contenant des valeurs numériques utilisées dans l'histogramme.
main indique le titre du graphique.
col est utilisé pour définir la couleur des barres.
border est utilisé pour définir la couleur de la bordure de chaque barre.
xlab est utilisé pour donner une description de l'axe des x.
xlim est utilisé pour spécifier la plage de valeurs sur l'axe des x.
ylim est utilisé pour spécifier la plage de valeurs sur l'axe y.
breaks est utilisé pour mentionner la largeur de chaque barre.
Exemple
Un histogramme simple est créé à l'aide des paramètres de vecteur d'entrée, d'étiquette, de col et de bordure.
Le script ci-dessous créera et enregistrera l'histogramme dans le répertoire de travail R actuel.
# Create data for the graph.
v <- c(9,13,21,8,36,22,12,41,31,33,19)
# Give the chart file a name.
png(file = "histogram.png")
# Create the histogram.
hist(v,xlab = "Weight",col = "yellow",border = "blue")
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
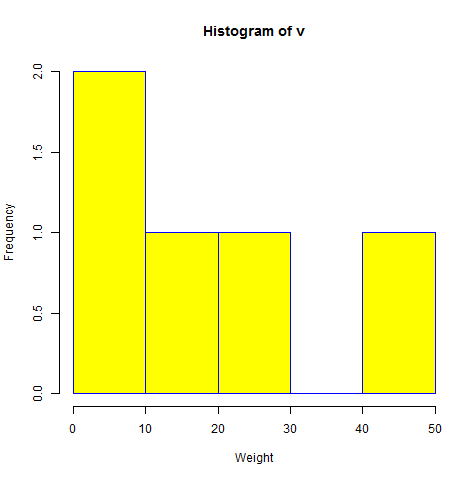
Plage de valeurs X et Y
Pour spécifier la plage de valeurs autorisées en axe X et axe Y, nous pouvons utiliser les paramètres xlim et ylim.
La largeur de chacune des barres peut être décidée en utilisant des pauses.
# Create data for the graph.
v <- c(9,13,21,8,36,22,12,41,31,33,19)
# Give the chart file a name.
png(file = "histogram_lim_breaks.png")
# Create the histogram.
hist(v,xlab = "Weight",col = "green",border = "red", xlim = c(0,40), ylim = c(0,5),
breaks = 5)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Un graphique linéaire est un graphique qui relie une série de points en dessinant des segments de ligne entre eux. Ces points sont classés dans l'une de leurs coordonnées (généralement la coordonnée x). Les graphiques linéaires sont généralement utilisés pour identifier les tendances des données.
le plot() La fonction dans R est utilisée pour créer le graphique linéaire.
Syntaxe
La syntaxe de base pour créer un graphique en courbes dans R est -
plot(v,type,col,xlab,ylab)Voici la description des paramètres utilisés -
v est un vecteur contenant les valeurs numériques.
type prend la valeur "p" pour dessiner uniquement les points, "l" pour dessiner uniquement les lignes et "o" pour dessiner à la fois les points et les lignes.
xlab est l'étiquette de l'axe x.
ylab est l'étiquette de l'axe y.
main est le titre du graphique.
col est utilisé pour donner des couleurs aux points et aux lignes.
Exemple
Un graphique linéaire simple est créé en utilisant le vecteur d'entrée et le paramètre de type "O". Le script ci-dessous créera et enregistrera un graphique en courbes dans le répertoire de travail R actuel.
# Create the data for the chart.
v <- c(7,12,28,3,41)
# Give the chart file a name.
png(file = "line_chart.jpg")
# Plot the bar chart.
plot(v,type = "o")
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Titre, couleur et étiquettes du graphique en courbes
Les fonctionnalités du graphique linéaire peuvent être développées à l'aide de paramètres supplémentaires. Nous ajoutons de la couleur aux points et aux lignes, donnons un titre au graphique et ajoutons des étiquettes aux axes.
Exemple
# Create the data for the chart.
v <- c(7,12,28,3,41)
# Give the chart file a name.
png(file = "line_chart_label_colored.jpg")
# Plot the bar chart.
plot(v,type = "o", col = "red", xlab = "Month", ylab = "Rain fall",
main = "Rain fall chart")
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Plusieurs lignes dans un graphique en courbes
Plusieurs lignes peuvent être tracées sur le même graphique en utilisant le lines()fonction.
Une fois la première ligne tracée, la fonction lines () peut utiliser un vecteur supplémentaire comme entrée pour dessiner la deuxième ligne dans le graphique,
# Create the data for the chart.
v <- c(7,12,28,3,41)
t <- c(14,7,6,19,3)
# Give the chart file a name.
png(file = "line_chart_2_lines.jpg")
# Plot the bar chart.
plot(v,type = "o",col = "red", xlab = "Month", ylab = "Rain fall",
main = "Rain fall chart")
lines(t, type = "o", col = "blue")
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Les nuages de points montrent de nombreux points tracés dans le plan cartésien. Chaque point représente les valeurs de deux variables. Une variable est choisie dans l'axe horizontal et une autre dans l'axe vertical.
Le nuage de points simple est créé à l'aide du plot() fonction.
Syntaxe
La syntaxe de base pour créer un nuage de points dans R est -
plot(x, y, main, xlab, ylab, xlim, ylim, axes)Voici la description des paramètres utilisés -
x est l'ensemble de données dont les valeurs sont les coordonnées horizontales.
y est l'ensemble de données dont les valeurs sont les coordonnées verticales.
main est la tuile du graphique.
xlab est le libellé sur l'axe horizontal.
ylab est l'étiquette dans l'axe vertical.
xlim est les limites des valeurs de x utilisées pour le traçage.
ylim est les limites des valeurs de y utilisées pour le traçage.
axes indique si les deux axes doivent être dessinés sur le graphique.
Exemple
Nous utilisons l'ensemble de données "mtcars"disponible dans l'environnement R pour créer un nuage de points de base. Utilisons les colonnes "wt" et "mpg" dans mtcars.
input <- mtcars[,c('wt','mpg')]
print(head(input))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
wt mpg
Mazda RX4 2.620 21.0
Mazda RX4 Wag 2.875 21.0
Datsun 710 2.320 22.8
Hornet 4 Drive 3.215 21.4
Hornet Sportabout 3.440 18.7
Valiant 3.460 18.1Création du nuage de points
Le script ci-dessous créera un diagramme de dispersion pour la relation entre poids (poids) et mpg (miles par gallon).
# Get the input values.
input <- mtcars[,c('wt','mpg')]
# Give the chart file a name.
png(file = "scatterplot.png")
# Plot the chart for cars with weight between 2.5 to 5 and mileage between 15 and 30.
plot(x = input$wt,y = input$mpg,
xlab = "Weight",
ylab = "Milage",
xlim = c(2.5,5),
ylim = c(15,30),
main = "Weight vs Milage"
)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Matrices de nuages de points
Lorsque nous avons plus de deux variables et que nous voulons trouver la corrélation entre une variable et les autres, nous utilisons une matrice de nuage de points. Nous utilisonspairs() fonction pour créer des matrices de nuages de points.
Syntaxe
La syntaxe de base pour créer des matrices de nuage de points dans R est -
pairs(formula, data)Voici la description des paramètres utilisés -
formula représente la série de variables utilisées par paires.
data représente l'ensemble de données à partir duquel les variables seront extraites.
Exemple
Chaque variable est associée à chacune des variables restantes. Un nuage de points est tracé pour chaque paire.
# Give the chart file a name.
png(file = "scatterplot_matrices.png")
# Plot the matrices between 4 variables giving 12 plots.
# One variable with 3 others and total 4 variables.
pairs(~wt+mpg+disp+cyl,data = mtcars,
main = "Scatterplot Matrix")
# Save the file.
dev.off()Lorsque le code ci-dessus est exécuté, nous obtenons la sortie suivante.
L'analyse statistique dans R est effectuée à l'aide de nombreuses fonctions intégrées. La plupart de ces fonctions font partie du package de base R. Ces fonctions prennent le vecteur R comme entrée avec les arguments et donnent le résultat.
Les fonctions dont nous discutons dans ce chapitre sont la moyenne, la médiane et le mode.
Signifier
Il est calculé en prenant la somme des valeurs et en divisant par le nombre de valeurs dans une série de données.
La fonction mean() est utilisé pour calculer cela dans R.
Syntaxe
La syntaxe de base pour calculer la moyenne dans R est -
mean(x, trim = 0, na.rm = FALSE, ...)Voici la description des paramètres utilisés -
x est le vecteur d'entrée.
trim est utilisé pour supprimer certaines observations des deux extrémités du vecteur trié.
na.rm est utilisé pour supprimer les valeurs manquantes du vecteur d'entrée.
Exemple
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find Mean.
result.mean <- mean(x)
print(result.mean)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 8.22Application de l'option de coupe
Lorsque le paramètre trim est fourni, les valeurs du vecteur sont triées, puis le nombre requis d'observations est supprimé du calcul de la moyenne.
Lorsque trim = 0,3, 3 valeurs de chaque extrémité seront supprimées des calculs pour trouver la moyenne.
Dans ce cas, le vecteur trié est (−21, −5, 2, 3, 4,2, 7, 8, 12, 18, 54) et les valeurs retirées du vecteur pour le calcul de la moyenne sont (−21, −5,2) de gauche et (12,18,54) de droite.
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find Mean.
result.mean <- mean(x,trim = 0.3)
print(result.mean)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 5.55Application de l'option NA
S'il y a des valeurs manquantes, la fonction moyenne renvoie NA.
Pour supprimer les valeurs manquantes du calcul, utilisez na.rm = TRUE. ce qui signifie supprimer les valeurs NA.
# Create a vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5,NA)
# Find mean.
result.mean <- mean(x)
print(result.mean)
# Find mean dropping NA values.
result.mean <- mean(x,na.rm = TRUE)
print(result.mean)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] NA
[1] 8.22Médian
La valeur la plus médiane d'une série de données est appelée la médiane. lemedian() La fonction est utilisée dans R pour calculer cette valeur.
Syntaxe
La syntaxe de base pour calculer la médiane dans R est -
median(x, na.rm = FALSE)Voici la description des paramètres utilisés -
x est le vecteur d'entrée.
na.rm est utilisé pour supprimer les valeurs manquantes du vecteur d'entrée.
Exemple
# Create the vector.
x <- c(12,7,3,4.2,18,2,54,-21,8,-5)
# Find the median.
median.result <- median(x)
print(median.result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 5.6Mode
Le mode est la valeur qui a le plus grand nombre d'occurrences dans un ensemble de données. Contrairement à la moyenne et à la médiane, le mode peut avoir à la fois des données numériques et des caractères.
R n'a pas de fonction intégrée standard pour calculer le mode. Nous créons donc une fonction utilisateur pour calculer le mode d'un ensemble de données dans R. Cette fonction prend le vecteur en entrée et donne la valeur du mode en sortie.
Exemple
# Create the function.
getmode <- function(v) {
uniqv <- unique(v)
uniqv[which.max(tabulate(match(v, uniqv)))]
}
# Create the vector with numbers.
v <- c(2,1,2,3,1,2,3,4,1,5,5,3,2,3)
# Calculate the mode using the user function.
result <- getmode(v)
print(result)
# Create the vector with characters.
charv <- c("o","it","the","it","it")
# Calculate the mode using the user function.
result <- getmode(charv)
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 2
[1] "it"L'analyse de régression est un outil statistique très largement utilisé pour établir un modèle de relation entre deux variables. L'une de ces variables est appelée variable prédictive dont la valeur est recueillie par des expériences. L'autre variable est appelée variable de réponse dont la valeur est dérivée de la variable prédictive.
Dans la régression linéaire, ces deux variables sont liées par une équation, où l'exposant (puissance) de ces deux variables est 1. Mathématiquement, une relation linéaire représente une ligne droite lorsqu'elle est tracée sous forme de graphique. Une relation non linéaire où l'exposant d'une variable n'est pas égal à 1 crée une courbe.
L'équation mathématique générale pour une régression linéaire est -
y = ax + bVoici la description des paramètres utilisés -
y est la variable de réponse.
x est la variable prédictive.
a et b sont des constantes que l'on appelle les coefficients.
Étapes pour établir une régression
Un exemple simple de régression consiste à prédire le poids d'une personne lorsque sa taille est connue. Pour ce faire, nous devons avoir la relation entre la taille et le poids d'une personne.
Les étapes pour créer la relation sont -
Réalisez l'expérience de collecte d'un échantillon de valeurs observées de taille et de poids correspondant.
Créez un modèle de relation à l'aide du lm() fonctions dans R.
Trouvez les coefficients du modèle créé et créez l'équation mathématique à l'aide de ces
Obtenez un résumé du modèle de relation pour connaître l'erreur moyenne de prédiction. Aussi appeléresiduals.
Pour prédire le poids des nouvelles personnes, utilisez le predict() fonction dans R.
Des données d'entrée
Voici les exemples de données représentant les observations -
# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131
# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48Fonction lm ()
Cette fonction crée le modèle de relation entre le prédicteur et la variable de réponse.
Syntaxe
La syntaxe de base pour lm() la fonction en régression linéaire est -
lm(formula,data)Voici la description des paramètres utilisés -
formula est un symbole présentant la relation entre x et y.
data est le vecteur sur lequel la formule sera appliquée.
Créer un modèle de relation et obtenir les coefficients
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(relation)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-38.4551 0.6746Obtenez le résumé de la relation
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
print(summary(relation))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-6.3002 -1.6629 0.0412 1.8944 3.9775
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -38.45509 8.04901 -4.778 0.00139 **
x 0.67461 0.05191 12.997 1.16e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared: 0.9548, Adjusted R-squared: 0.9491
F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06Predire () Fonction
Syntaxe
La syntaxe de base de prédire () dans la régression linéaire est -
predict(object, newdata)Voici la description des paramètres utilisés -
object est la formule déjà créée à l'aide de la fonction lm ().
newdata est le vecteur contenant la nouvelle valeur de la variable prédictive.
Prédire le poids des nouvelles personnes
# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
# Apply the lm() function.
relation <- lm(y~x)
# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <- predict(relation,a)
print(result)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
1
76.22869Visualisez graphiquement la régression
# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)
# Give the chart file a name.
png(file = "linearregression.png")
# Plot the chart.
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
La régression multiple est une extension de la régression linéaire en relation entre plus de deux variables. Dans une relation linéaire simple, nous avons un prédicteur et une variable de réponse, mais dans la régression multiple, nous avons plus d'une variable de prédicteur et une variable de réponse.
L'équation mathématique générale de la régression multiple est -
y = a + b1x1 + b2x2 +...bnxnVoici la description des paramètres utilisés -
y est la variable de réponse.
a, b1, b2...bn sont les coefficients.
x1, x2, ...xn sont les variables prédictives.
Nous créons le modèle de régression en utilisant le lm()fonction en R. Le modèle détermine la valeur des coefficients en utilisant les données d'entrée. Ensuite, nous pouvons prédire la valeur de la variable de réponse pour un ensemble donné de variables prédictives en utilisant ces coefficients.
Fonction lm ()
Cette fonction crée le modèle de relation entre le prédicteur et la variable de réponse.
Syntaxe
La syntaxe de base pour lm() la fonction en régression multiple est -
lm(y ~ x1+x2+x3...,data)Voici la description des paramètres utilisés -
formula est un symbole présentant la relation entre la variable de réponse et les variables prédictives.
data est le vecteur sur lequel la formule sera appliquée.
Exemple
Des données d'entrée
Considérez l'ensemble de données "mtcars" disponible dans l'environnement R. Il donne une comparaison entre les différents modèles de voitures en termes de kilométrage par gallon (mpg), cylindrée ("disp"), puissance ("hp"), poids de la voiture ("wt") et quelques autres paramètres.
Le but du modèle est d'établir la relation entre «mpg» en tant que variable de réponse avec «disp», «hp» et «wt» comme variables prédictives. Nous créons un sous-ensemble de ces variables à partir de l'ensemble de données mtcars à cet effet.
input <- mtcars[,c("mpg","disp","hp","wt")]
print(head(input))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
mpg disp hp wt
Mazda RX4 21.0 160 110 2.620
Mazda RX4 Wag 21.0 160 110 2.875
Datsun 710 22.8 108 93 2.320
Hornet 4 Drive 21.4 258 110 3.215
Hornet Sportabout 18.7 360 175 3.440
Valiant 18.1 225 105 3.460Créer un modèle de relation et obtenir les coefficients
input <- mtcars[,c("mpg","disp","hp","wt")]
# Create the relationship model.
model <- lm(mpg~disp+hp+wt, data = input)
# Show the model.
print(model)
# Get the Intercept and coefficients as vector elements.
cat("# # # # The Coefficient Values # # # ","\n")
a <- coef(model)[1]
print(a)
Xdisp <- coef(model)[2]
Xhp <- coef(model)[3]
Xwt <- coef(model)[4]
print(Xdisp)
print(Xhp)
print(Xwt)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Call:
lm(formula = mpg ~ disp + hp + wt, data = input)
Coefficients:
(Intercept) disp hp wt
37.105505 -0.000937 -0.031157 -3.800891
# # # # The Coefficient Values # # #
(Intercept)
37.10551
disp
-0.0009370091
hp
-0.03115655
wt
-3.800891Créer une équation pour le modèle de régression
Sur la base des valeurs d'intersection et de coefficient ci-dessus, nous créons l'équation mathématique.
Y = a+Xdisp.x1+Xhp.x2+Xwt.x3
or
Y = 37.15+(-0.000937)*x1+(-0.0311)*x2+(-3.8008)*x3Appliquer l'équation pour prédire les nouvelles valeurs
Nous pouvons utiliser l'équation de régression créée ci-dessus pour prédire le kilométrage lorsqu'un nouvel ensemble de valeurs de déplacement, de puissance et de poids est fourni.
Pour une voiture avec disp = 221, hp = 102 et wt = 2,91, le kilométrage prévu est -
Y = 37.15+(-0.000937)*221+(-0.0311)*102+(-3.8008)*2.91 = 22.7104La régression logistique est un modèle de régression dans lequel la variable de réponse (variable dépendante) a des valeurs catégorielles telles que Vrai / Faux ou 0/1. Il mesure en fait la probabilité d'une réponse binaire comme la valeur de la variable de réponse basée sur l'équation mathématique la reliant aux variables prédictives.
L'équation mathématique générale de la régression logistique est -
y = 1/(1+e^-(a+b1x1+b2x2+b3x3+...))Voici la description des paramètres utilisés -
y est la variable de réponse.
x est la variable prédictive.
a et b sont les coefficients qui sont des constantes numériques.
La fonction utilisée pour créer le modèle de régression est la glm() fonction.
Syntaxe
La syntaxe de base pour glm() la fonction de régression logistique est -
glm(formula,data,family)Voici la description des paramètres utilisés -
formula est le symbole présentant la relation entre les variables.
data est l'ensemble de données donnant les valeurs de ces variables.
familyest un objet R pour spécifier les détails du modèle. Sa valeur est binomiale pour la régression logistique.
Exemple
L'ensemble de données intégré «mtcars» décrit différents modèles de voitures avec leurs diverses spécifications de moteur. Dans le jeu de données "mtcars", le mode de transmission (automatique ou manuel) est décrit par la colonne am qui est une valeur binaire (0 ou 1). Nous pouvons créer un modèle de régression logistique entre les colonnes "am" et 3 autres colonnes - hp, wt et cyl.
# Select some columns form mtcars.
input <- mtcars[,c("am","cyl","hp","wt")]
print(head(input))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
am cyl hp wt
Mazda RX4 1 6 110 2.620
Mazda RX4 Wag 1 6 110 2.875
Datsun 710 1 4 93 2.320
Hornet 4 Drive 0 6 110 3.215
Hornet Sportabout 0 8 175 3.440
Valiant 0 6 105 3.460Créer un modèle de régression
Nous utilisons le glm() fonction pour créer le modèle de régression et obtenir son résumé pour analyse.
input <- mtcars[,c("am","cyl","hp","wt")]
am.data = glm(formula = am ~ cyl + hp + wt, data = input, family = binomial)
print(summary(am.data))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Call:
glm(formula = am ~ cyl + hp + wt, family = binomial, data = input)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.17272 -0.14907 -0.01464 0.14116 1.27641
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 19.70288 8.11637 2.428 0.0152 *
cyl 0.48760 1.07162 0.455 0.6491
hp 0.03259 0.01886 1.728 0.0840 .
wt -9.14947 4.15332 -2.203 0.0276 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 43.2297 on 31 degrees of freedom
Residual deviance: 9.8415 on 28 degrees of freedom
AIC: 17.841
Number of Fisher Scoring iterations: 8Conclusion
Dans le résumé comme la valeur p de la dernière colonne est supérieure à 0,05 pour les variables "cyl" et "hp", nous les considérons comme insignifiantes pour contribuer à la valeur de la variable "am". Seul le poids (wt) influe sur la valeur «am» dans ce modèle de régression.
Dans une collecte aléatoire de données provenant de sources indépendantes, on observe généralement que la distribution des données est normale. Ce qui signifie que, en traçant un graphique avec la valeur de la variable sur l'axe horizontal et le décompte des valeurs sur l'axe vertical, nous obtenons une courbe en forme de cloche. Le centre de la courbe représente la moyenne de l'ensemble de données. Dans le graphique, cinquante pour cent des valeurs se trouvent à gauche de la moyenne et les cinquante pour cent restants se trouvent à droite du graphique. C'est ce qu'on appelle la distribution normale dans les statistiques.
R a quatre fonctions intégrées pour générer une distribution normale. Ils sont décrits ci-dessous.
dnorm(x, mean, sd)
pnorm(x, mean, sd)
qnorm(p, mean, sd)
rnorm(n, mean, sd)Voici la description des paramètres utilisés dans les fonctions ci-dessus -
x est un vecteur de nombres.
p est un vecteur de probabilités.
n est le nombre d'observations (taille de l'échantillon).
meanest la valeur moyenne des données d'échantillon. Sa valeur par défaut est zéro.
sdest l'écart type. Sa valeur par défaut est 1.
dnorm ()
Cette fonction donne la hauteur de la distribution de probabilité à chaque point pour une moyenne et un écart type donnés.
# Create a sequence of numbers between -10 and 10 incrementing by 0.1.
x <- seq(-10, 10, by = .1)
# Choose the mean as 2.5 and standard deviation as 0.5.
y <- dnorm(x, mean = 2.5, sd = 0.5)
# Give the chart file a name.
png(file = "dnorm.png")
plot(x,y)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
pnorm ()
Cette fonction donne la probabilité qu'un nombre aléatoire normalement distribué soit inférieur à la valeur d'un nombre donné. Elle est également appelée "Fonction de distribution cumulative".
# Create a sequence of numbers between -10 and 10 incrementing by 0.2.
x <- seq(-10,10,by = .2)
# Choose the mean as 2.5 and standard deviation as 2.
y <- pnorm(x, mean = 2.5, sd = 2)
# Give the chart file a name.
png(file = "pnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
qnorm ()
Cette fonction prend la valeur de probabilité et donne un nombre dont la valeur cumulée correspond à la valeur de probabilité.
# Create a sequence of probability values incrementing by 0.02.
x <- seq(0, 1, by = 0.02)
# Choose the mean as 2 and standard deviation as 3.
y <- qnorm(x, mean = 2, sd = 1)
# Give the chart file a name.
png(file = "qnorm.png")
# Plot the graph.
plot(x,y)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
rnorm ()
Cette fonction permet de générer des nombres aléatoires dont la distribution est normale. Il prend la taille de l'échantillon comme entrée et génère autant de nombres aléatoires. Nous dessinons un histogramme pour montrer la distribution des nombres générés.
# Create a sample of 50 numbers which are normally distributed.
y <- rnorm(50)
# Give the chart file a name.
png(file = "rnorm.png")
# Plot the histogram for this sample.
hist(y, main = "Normal DIstribution")
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Le modèle de distribution binomiale traite de la recherche de la probabilité de succès d'un événement qui n'a que deux résultats possibles dans une série d'expériences. Par exemple, lancer une pièce donne toujours une tête ou une queue. La probabilité de trouver exactement 3 têtes en lançant une pièce à plusieurs reprises pendant 10 fois est estimée au cours de la distribution binomiale.
R a quatre fonctions intégrées pour générer une distribution binomiale. Ils sont décrits ci-dessous.
dbinom(x, size, prob)
pbinom(x, size, prob)
qbinom(p, size, prob)
rbinom(n, size, prob)Voici la description des paramètres utilisés -
x est un vecteur de nombres.
p est un vecteur de probabilités.
n est le nombre d'observations.
size est le nombre d'essais.
prob est la probabilité de succès de chaque essai.
dbinom ()
Cette fonction donne la distribution de densité de probabilité à chaque point.
# Create a sample of 50 numbers which are incremented by 1.
x <- seq(0,50,by = 1)
# Create the binomial distribution.
y <- dbinom(x,50,0.5)
# Give the chart file a name.
png(file = "dbinom.png")
# Plot the graph for this sample.
plot(x,y)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
pbinom ()
Cette fonction donne la probabilité cumulée d'un événement. C'est une valeur unique représentant la probabilité.
# Probability of getting 26 or less heads from a 51 tosses of a coin.
x <- pbinom(26,51,0.5)
print(x)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 0.610116qbinom ()
Cette fonction prend la valeur de probabilité et donne un nombre dont la valeur cumulée correspond à la valeur de probabilité.
# How many heads will have a probability of 0.25 will come out when a coin
# is tossed 51 times.
x <- qbinom(0.25,51,1/2)
print(x)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 23rbinom ()
Cette fonction génère le nombre requis de valeurs aléatoires d'une probabilité donnée à partir d'un échantillon donné.
# Find 8 random values from a sample of 150 with probability of 0.4.
x <- rbinom(8,150,.4)
print(x)Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 58 61 59 66 55 60 61 67La régression de Poisson implique des modèles de régression dans lesquels la variable de réponse se présente sous la forme de nombres et non de nombres fractionnaires. Par exemple, le nombre de naissances ou le nombre de victoires dans une série de matchs de football. Les valeurs des variables de réponse suivent également une distribution de Poisson.
L'équation mathématique générale de la régression de Poisson est -
log(y) = a + b1x1 + b2x2 + bnxn.....Voici la description des paramètres utilisés -
y est la variable de réponse.
a et b sont les coefficients numériques.
x est la variable prédictive.
La fonction utilisée pour créer le modèle de régression de Poisson est la glm() fonction.
Syntaxe
La syntaxe de base pour glm() La fonction dans la régression de Poisson est -
glm(formula,data,family)Voici la description des paramètres utilisés dans les fonctions ci-dessus -
formula est le symbole présentant la relation entre les variables.
data est l'ensemble de données donnant les valeurs de ces variables.
familyest un objet R pour spécifier les détails du modèle. Sa valeur est «Poisson» pour la régression logistique.
Exemple
Nous avons le jeu de données intégré "warpbreaks" qui décrit l'effet du type de laine (A ou B) et de la tension (faible, moyenne ou élevée) sur le nombre de cassures de chaîne par métier. Considérons les "pauses" comme la variable de réponse qui est un décompte du nombre de pauses. Le "type" et la "tension" de la laine sont considérés comme des variables prédictives.
Input Data
input <- warpbreaks
print(head(input))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
breaks wool tension
1 26 A L
2 30 A L
3 54 A L
4 25 A L
5 70 A L
6 52 A LCréer un modèle de régression
output <-glm(formula = breaks ~ wool+tension, data = warpbreaks,
family = poisson)
print(summary(output))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Call:
glm(formula = breaks ~ wool + tension, family = poisson, data = warpbreaks)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.6871 -1.6503 -0.4269 1.1902 4.2616
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.69196 0.04541 81.302 < 2e-16 ***
woolB -0.20599 0.05157 -3.994 6.49e-05 ***
tensionM -0.32132 0.06027 -5.332 9.73e-08 ***
tensionH -0.51849 0.06396 -8.107 5.21e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 297.37 on 53 degrees of freedom
Residual deviance: 210.39 on 50 degrees of freedom
AIC: 493.06
Number of Fisher Scoring iterations: 4Dans le résumé, nous recherchons la valeur de p dans la dernière colonne comme étant inférieure à 0,05 pour tenir compte d'un impact de la variable de prédiction sur la variable de réponse. Comme on le voit, le type de laine B ayant des types de tension M et H a un impact sur le nombre de cassures.
Nous utilisons l'analyse de régression pour créer des modèles qui décrivent l'effet de la variation des variables prédictives sur la variable de réponse. Parfois, si nous avons une variable catégorielle avec des valeurs comme Oui / Non ou Homme / Femme, etc. L'analyse de régression simple donne plusieurs résultats pour chaque valeur de la variable catégorielle. Dans un tel scénario, nous pouvons étudier l'effet de la variable catégorielle en l'utilisant avec la variable prédictive et en comparant les lignes de régression pour chaque niveau de la variable catégorielle. Une telle analyse est appeléeAnalysis of Covariance aussi appelé comme ANCOVA.
Exemple
Considérez le jeu de données intégré R mtcars. On y observe que le champ "am" représente le type de transmission (automatique ou manuelle). Il s'agit d'une variable catégorielle avec des valeurs 0 et 1. La valeur en miles par gallon (mpg) d'une voiture peut également en dépendre en plus de la valeur de la puissance en chevaux ("hp").
Nous étudions l'effet de la valeur de "am" sur la régression entre "mpg" et "hp". Cela se fait en utilisant leaov() fonction suivie de la anova() fonction pour comparer les régressions multiples.
Des données d'entrée
Créez un bloc de données contenant les champs "mpg", "hp" et "am" du jeu de données mtcars. Ici, nous prenons "mpg" comme variable de réponse, "hp" comme variable prédictive et "am" comme variable catégorielle.
input <- mtcars[,c("am","mpg","hp")]
print(head(input))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
am mpg hp
Mazda RX4 1 21.0 110
Mazda RX4 Wag 1 21.0 110
Datsun 710 1 22.8 93
Hornet 4 Drive 0 21.4 110
Hornet Sportabout 0 18.7 175
Valiant 0 18.1 105Analyse ANCOVA
Nous créons un modèle de régression prenant "hp" comme variable prédictive et "mpg" comme variable de réponse en tenant compte de l'interaction entre "am" et "hp".
Modèle avec interaction entre la variable catégorielle et la variable prédictive
# Get the dataset.
input <- mtcars
# Create the regression model.
result <- aov(mpg~hp*am,data = input)
print(summary(result))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Df Sum Sq Mean Sq F value Pr(>F)
hp 1 678.4 678.4 77.391 1.50e-09 ***
am 1 202.2 202.2 23.072 4.75e-05 ***
hp:am 1 0.0 0.0 0.001 0.981
Residuals 28 245.4 8.8
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Ce résultat montre que la puissance en chevaux et le type de transmission ont un effet significatif sur les miles par gallon car la valeur p dans les deux cas est inférieure à 0,05. Mais l'interaction entre ces deux variables n'est pas significative car la valeur p est supérieure à 0,05.
Modèle sans interaction entre la variable catégorielle et la variable prédictive
# Get the dataset.
input <- mtcars
# Create the regression model.
result <- aov(mpg~hp+am,data = input)
print(summary(result))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Df Sum Sq Mean Sq F value Pr(>F)
hp 1 678.4 678.4 80.15 7.63e-10 ***
am 1 202.2 202.2 23.89 3.46e-05 ***
Residuals 29 245.4 8.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Ce résultat montre que la puissance en chevaux et le type de transmission ont un effet significatif sur les miles par gallon car la valeur p dans les deux cas est inférieure à 0,05.
Comparaison de deux modèles
Nous pouvons maintenant comparer les deux modèles pour conclure si l'interaction des variables est vraiment non significative. Pour cela, nous utilisons leanova() fonction.
# Get the dataset.
input <- mtcars
# Create the regression models.
result1 <- aov(mpg~hp*am,data = input)
result2 <- aov(mpg~hp+am,data = input)
# Compare the two models.
print(anova(result1,result2))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Model 1: mpg ~ hp * am
Model 2: mpg ~ hp + am
Res.Df RSS Df Sum of Sq F Pr(>F)
1 28 245.43
2 29 245.44 -1 -0.0052515 6e-04 0.9806Comme la valeur p est supérieure à 0,05, nous concluons que l'interaction entre la puissance en chevaux et le type de transmission n'est pas significative. Ainsi, le kilométrage par gallon dépendra de la même manière de la puissance de la voiture en mode de transmission automatique et manuelle.
La série chronologique est une série de points de données dans laquelle chaque point de données est associé à un horodatage. Un exemple simple est le prix d'une action sur le marché boursier à différents moments d'un jour donné. Un autre exemple est la quantité de précipitations dans une région à différents mois de l'année. Le langage R utilise de nombreuses fonctions pour créer, manipuler et tracer les données de séries chronologiques. Les données de la série chronologique sont stockées dans un objet R appelétime-series object. C'est aussi un objet de données R comme un vecteur ou une trame de données.
L'objet de série chronologique est créé à l'aide de ts() fonction.
Syntaxe
La syntaxe de base pour ts() La fonction dans l'analyse des séries chronologiques est -
timeseries.object.name <- ts(data, start, end, frequency)Voici la description des paramètres utilisés -
data est un vecteur ou une matrice contenant les valeurs utilisées dans la série chronologique.
start spécifie l'heure de début de la première observation de la série chronologique.
end spécifie l'heure de fin de la dernière observation de la série chronologique.
frequency spécifie le nombre d'observations par unité de temps.
A l'exception du paramètre "data", tous les autres paramètres sont facultatifs.
Exemple
Considérez les détails des précipitations annuelles à un endroit à partir de janvier 2012. Nous créons un objet de série temporelle R pour une période de 12 mois et le tracons.
# Get the data points in form of a R vector.
rainfall <- c(799,1174.8,865.1,1334.6,635.4,918.5,685.5,998.6,784.2,985,882.8,1071)
# Convert it to a time series object.
rainfall.timeseries <- ts(rainfall,start = c(2012,1),frequency = 12)
# Print the timeseries data.
print(rainfall.timeseries)
# Give the chart file a name.
png(file = "rainfall.png")
# Plot a graph of the time series.
plot(rainfall.timeseries)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, il produit le résultat et le graphique suivants -
Jan Feb Mar Apr May Jun Jul Aug Sep
2012 799.0 1174.8 865.1 1334.6 635.4 918.5 685.5 998.6 784.2
Oct Nov Dec
2012 985.0 882.8 1071.0Le graphique des séries chronologiques -
Différents intervalles de temps
La valeur du frequencyLe paramètre de la fonction ts () décide des intervalles de temps auxquels les points de données sont mesurés. Une valeur de 12 indique que la série chronologique porte sur 12 mois. Les autres valeurs et leur signification sont comme ci-dessous -
frequency = 12 calcule les points de données pour chaque mois de l'année.
frequency = 4 calcule les points de données pour chaque trimestre de l'année.
frequency = 6 fixe les points de données toutes les 10 minutes d'une heure.
frequency = 24*6 associe les points de données toutes les 10 minutes par jour.
Séries chronologiques multiples
Nous pouvons tracer plusieurs séries temporelles dans un graphique en combinant les deux séries dans une matrice.
# Get the data points in form of a R vector.
rainfall1 <- c(799,1174.8,865.1,1334.6,635.4,918.5,685.5,998.6,784.2,985,882.8,1071)
rainfall2 <-
c(655,1306.9,1323.4,1172.2,562.2,824,822.4,1265.5,799.6,1105.6,1106.7,1337.8)
# Convert them to a matrix.
combined.rainfall <- matrix(c(rainfall1,rainfall2),nrow = 12)
# Convert it to a time series object.
rainfall.timeseries <- ts(combined.rainfall,start = c(2012,1),frequency = 12)
# Print the timeseries data.
print(rainfall.timeseries)
# Give the chart file a name.
png(file = "rainfall_combined.png")
# Plot a graph of the time series.
plot(rainfall.timeseries, main = "Multiple Time Series")
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, il produit le résultat et le graphique suivants -
Series 1 Series 2
Jan 2012 799.0 655.0
Feb 2012 1174.8 1306.9
Mar 2012 865.1 1323.4
Apr 2012 1334.6 1172.2
May 2012 635.4 562.2
Jun 2012 918.5 824.0
Jul 2012 685.5 822.4
Aug 2012 998.6 1265.5
Sep 2012 784.2 799.6
Oct 2012 985.0 1105.6
Nov 2012 882.8 1106.7
Dec 2012 1071.0 1337.8Le graphique de séries chronologiques multiples -
Lors de la modélisation de données du monde réel pour l'analyse de régression, nous observons qu'il est rarement le cas que l'équation du modèle soit une équation linéaire donnant un graphe linéaire. La plupart du temps, l'équation du modèle de données du monde réel implique des fonctions mathématiques de degré supérieur comme un exposant de 3 ou une fonction sin. Dans un tel scénario, le tracé du modèle donne une courbe plutôt qu'une ligne. L'objectif de la régression linéaire et non linéaire est d'ajuster les valeurs des paramètres du modèle pour trouver la ligne ou la courbe qui se rapproche le plus de vos données. En trouvant ces valeurs, nous pourrons estimer la variable de réponse avec une bonne précision.
Dans la régression des moindres carrés, nous établissons un modèle de régression dans lequel la somme des carrés des distances verticales de différents points de la courbe de régression est minimisée. Nous commençons généralement avec un modèle défini et supposons quelques valeurs pour les coefficients. Nous appliquons ensuite lenls() fonction de R pour obtenir les valeurs les plus précises avec les intervalles de confiance.
Syntaxe
La syntaxe de base pour créer un test des moindres carrés non linéaire dans R est -
nls(formula, data, start)Voici la description des paramètres utilisés -
formula est une formule de modèle non linéaire comprenant des variables et des paramètres.
data est une base de données utilisée pour évaluer les variables de la formule.
start est une liste nommée ou un vecteur numérique nommé d'estimations de départ.
Exemple
Nous considérerons un modèle non linéaire avec hypothèse des valeurs initiales de ses coefficients. Ensuite, nous verrons quels sont les intervalles de confiance de ces valeurs supposées afin que nous puissions juger dans quelle mesure ces valeurs intègrent le modèle.
Considérons donc l'équation ci-dessous à cet effet -
a = b1*x^2+b2Supposons que les coefficients initiaux soient 1 et 3 et ajustons ces valeurs dans la fonction nls ().
xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)
# Give the chart file a name.
png(file = "nls.png")
# Plot these values.
plot(xvalues,yvalues)
# Take the assumed values and fit into the model.
model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))
# Plot the chart with new data by fitting it to a prediction from 100 data points.
new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
lines(new.data$xvalues,predict(model,newdata = new.data))
# Save the file.
dev.off()
# Get the sum of the squared residuals.
print(sum(resid(model)^2))
# Get the confidence intervals on the chosen values of the coefficients.
print(confint(model))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
[1] 1.081935
Waiting for profiling to be done...
2.5% 97.5%
b1 1.137708 1.253135
b2 1.497364 2.496484
On peut en conclure que la valeur de b1 est plus proche de 1 tandis que la valeur de b2 est plus proche de 2 et non de 3.
L'arbre de décision est un graphique pour représenter les choix et leurs résultats sous la forme d'un arbre. Les nœuds du graphique représentent un événement ou un choix et les bords du graphique représentent les règles ou conditions de décision. Il est principalement utilisé dans les applications d'apprentissage automatique et d'exploration de données utilisant R.
Des exemples d'utilisation de la décision décisionnelle sont: prédire un e-mail comme spam ou non, prédire qu'une tumeur est cancéreuse ou prédire un prêt comme un bon ou un mauvais risque de crédit en fonction des facteurs de chacun. En règle générale, un modèle est créé avec des données observées également appelées données d'entraînement. Ensuite, un ensemble de données de validation est utilisé pour vérifier et améliorer le modèle. R a des packages qui sont utilisés pour créer et visualiser des arbres de décision. Pour un nouvel ensemble de variables prédictives, nous utilisons ce modèle pour arriver à une décision sur la catégorie (oui / non, spam / non spam) des données.
Le package R "party" est utilisé pour créer des arbres de décision.
Installer le package R
Utilisez la commande ci-dessous dans la console R pour installer le package. Vous devez également installer les packages dépendants, le cas échéant.
install.packages("party")Le package "party" a la fonction ctree() qui est utilisé pour créer et analyser l'arbre de décision.
Syntaxe
La syntaxe de base pour créer un arbre de décision dans R est -
ctree(formula, data)Voici la description des paramètres utilisés -
formula est une formule décrivant les variables de prédiction et de réponse.
data est le nom de l'ensemble de données utilisé.
Des données d'entrée
Nous utiliserons l'ensemble de données intégré R nommé readingSkillspour créer un arbre de décision. Il décrit le score des compétences en lecture d'une personne si nous connaissons les variables «âge», «taille des chaussures», «score» et si la personne est ou non un locuteur natif.
Voici les exemples de données.
# Load the party package. It will automatically load other
# dependent packages.
library(party)
# Print some records from data set readingSkills.
print(head(readingSkills))Lorsque nous exécutons le code ci-dessus, il produit le résultat et le graphique suivants -
nativeSpeaker age shoeSize score
1 yes 5 24.83189 32.29385
2 yes 6 25.95238 36.63105
3 no 11 30.42170 49.60593
4 yes 7 28.66450 40.28456
5 yes 11 31.88207 55.46085
6 yes 10 30.07843 52.83124
Loading required package: methods
Loading required package: grid
...............................
...............................Exemple
Nous utiliserons le ctree() fonction pour créer l'arbre de décision et voir son graphique.
# Load the party package. It will automatically load other
# dependent packages.
library(party)
# Create the input data frame.
input.dat <- readingSkills[c(1:105),]
# Give the chart file a name.
png(file = "decision_tree.png")
# Create the tree.
output.tree <- ctree(
nativeSpeaker ~ age + shoeSize + score,
data = input.dat)
# Plot the tree.
plot(output.tree)
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
null device
1
Loading required package: methods
Loading required package: grid
Loading required package: mvtnorm
Loading required package: modeltools
Loading required package: stats4
Loading required package: strucchange
Loading required package: zoo
Attaching package: ‘zoo’
The following objects are masked from ‘package:base’:
as.Date, as.Date.numeric
Loading required package: sandwich
Conclusion
À partir de l'arbre de décision présenté ci-dessus, nous pouvons conclure que toute personne dont le score de ReadingSkills est inférieur à 38,3 et dont l'âge est supérieur à 6 n'est pas un locuteur natif.
Dans l'approche de forêt aléatoire, un grand nombre d'arbres de décision sont créés. Chaque observation est introduite dans chaque arbre de décision. Le résultat le plus courant pour chaque observation est utilisé comme résultat final. Une nouvelle observation est introduite dans tous les arbres et prend un vote majoritaire pour chaque modèle de classification.
Une estimation d'erreur est faite pour les cas qui n'ont pas été utilisés lors de la construction de l'arbre. Cela s'appelle unOOB (Out-of-bag) estimation d'erreur qui est mentionnée en pourcentage.
Le package R "randomForest" est utilisé pour créer des forêts aléatoires.
Installer le package R
Utilisez la commande ci-dessous dans la console R pour installer le package. Vous devez également installer les packages dépendants, le cas échéant.
install.packages("randomForest)Le package "randomForest" a la fonction randomForest() qui est utilisé pour créer et analyser des forêts aléatoires.
Syntaxe
La syntaxe de base pour créer une forêt aléatoire dans R est -
randomForest(formula, data)Voici la description des paramètres utilisés -
formula est une formule décrivant les variables de prédiction et de réponse.
data est le nom de l'ensemble de données utilisé.
Des données d'entrée
Nous utiliserons l'ensemble de données intégré R nommé readingSkills pour créer un arbre de décision. Il décrit le score des compétences en lecture d'une personne si nous connaissons les variables «âge», «taille des chaussures», «score» et si la personne est un locuteur natif.
Voici les exemples de données.
# Load the party package. It will automatically load other
# required packages.
library(party)
# Print some records from data set readingSkills.
print(head(readingSkills))Lorsque nous exécutons le code ci-dessus, il produit le résultat et le graphique suivants -
nativeSpeaker age shoeSize score
1 yes 5 24.83189 32.29385
2 yes 6 25.95238 36.63105
3 no 11 30.42170 49.60593
4 yes 7 28.66450 40.28456
5 yes 11 31.88207 55.46085
6 yes 10 30.07843 52.83124
Loading required package: methods
Loading required package: grid
...............................
...............................Exemple
Nous utiliserons le randomForest() fonction pour créer l'arbre de décision et voir son graphique.
# Load the party package. It will automatically load other
# required packages.
library(party)
library(randomForest)
# Create the forest.
output.forest <- randomForest(nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
# View the forest results.
print(output.forest)
# Importance of each predictor.
print(importance(fit,type = 2))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Call:
randomForest(formula = nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 1
OOB estimate of error rate: 1%
Confusion matrix:
no yes class.error
no 99 1 0.01
yes 1 99 0.01
MeanDecreaseGini
age 13.95406
shoeSize 18.91006
score 56.73051Conclusion
À partir de la forêt aléatoire montrée ci-dessus, nous pouvons conclure que la taille des chaussures et le score sont les facteurs importants pour décider si quelqu'un est ou non un locuteur natif. De plus, le modèle n'a qu'une erreur de 1%, ce qui signifie que nous pouvons prédire avec une précision de 99%.
L'analyse de survie consiste à prévoir le moment où un événement spécifique va se produire. Elle est également connue sous le nom d'analyse du temps de défaillance ou d'analyse du temps mort. Par exemple, prédire le nombre de jours pendant lesquels une personne atteinte de cancer survivra ou prévoir le moment où un système mécanique échouera.
Le package R nommé survivalest utilisé pour effectuer une analyse de survie. Ce package contient la fonctionSurv()qui prend les données d'entrée comme une formule R et crée un objet de survie parmi les variables choisies pour l'analyse. Ensuite, nous utilisons la fonctionsurvfit() pour créer un tracé pour l'analyse.
Installer le paquet
install.packages("survival")Syntaxe
La syntaxe de base pour créer une analyse de survie dans R est -
Surv(time,event)
survfit(formula)Voici la description des paramètres utilisés -
time est le temps de suivi jusqu'à ce que l'événement se produise.
event indique l'état d'occurrence de l'événement attendu.
formula est la relation entre les variables prédictives.
Exemple
Nous considérerons l'ensemble de données nommé "pbc" présent dans les packages de survie installés ci-dessus. Il décrit les points de données de survie des personnes atteintes de cirrhose biliaire primitive (CBP) du foie. Parmi les nombreuses colonnes présentes dans le jeu de données, nous nous intéressons principalement aux champs «heure» et «statut». Le temps représente le nombre de jours entre l'enregistrement du patient et le début de l'événement entre le patient recevant une transplantation hépatique ou le décès du patient.
# Load the library.
library("survival")
# Print first few rows.
print(head(pbc))Lorsque nous exécutons le code ci-dessus, il produit le résultat et le graphique suivants -
id time status trt age sex ascites hepato spiders edema bili chol
1 1 400 2 1 58.76523 f 1 1 1 1.0 14.5 261
2 2 4500 0 1 56.44627 f 0 1 1 0.0 1.1 302
3 3 1012 2 1 70.07255 m 0 0 0 0.5 1.4 176
4 4 1925 2 1 54.74059 f 0 1 1 0.5 1.8 244
5 5 1504 1 2 38.10541 f 0 1 1 0.0 3.4 279
6 6 2503 2 2 66.25873 f 0 1 0 0.0 0.8 248
albumin copper alk.phos ast trig platelet protime stage
1 2.60 156 1718.0 137.95 172 190 12.2 4
2 4.14 54 7394.8 113.52 88 221 10.6 3
3 3.48 210 516.0 96.10 55 151 12.0 4
4 2.54 64 6121.8 60.63 92 183 10.3 4
5 3.53 143 671.0 113.15 72 136 10.9 3
6 3.98 50 944.0 93.00 63 NA 11.0 3À partir des données ci-dessus, nous considérons le temps et le statut pour notre analyse.
Application de la fonction Surv () et survfit ()
Nous procédons maintenant à l'application du Surv() fonction à l'ensemble de données ci-dessus et créez un graphique qui montrera la tendance.
# Load the library.
library("survival")
# Create the survival object.
survfit(Surv(pbc$time,pbc$status == 2)~1) # Give the chart file a name. png(file = "survival.png") # Plot the graph. plot(survfit(Surv(pbc$time,pbc$status == 2)~1))
# Save the file.
dev.off()Lorsque nous exécutons le code ci-dessus, il produit le résultat et le graphique suivants -
Call: survfit(formula = Surv(pbc$time, pbc$status == 2) ~ 1)
n events median 0.95LCL 0.95UCL
418 161 3395 3090 3853
La tendance du graphique ci-dessus nous aide à prédire la probabilité de survie au bout d'un certain nombre de jours.
Chi-Square testest une méthode statistique pour déterminer si deux variables catégorielles ont une corrélation significative entre elles. Ces deux variables doivent provenir de la même population et doivent être catégoriques telles que - Oui / Non, Homme / Femme, Rouge / Vert, etc.
Par exemple, nous pouvons construire un ensemble de données avec des observations sur le modèle d'achat de crème glacée des gens et essayer de corréler le sexe d'une personne avec la saveur de la glace qu'elle préfère. Si une corrélation est trouvée, nous pouvons planifier un stock approprié de saveurs en connaissant le nombre de sexe des visiteurs.
Syntaxe
La fonction utilisée pour effectuer le test du chi carré est chisq.test().
La syntaxe de base pour créer un test du chi carré dans R est -
chisq.test(data)Voici la description des paramètres utilisés -
data sont les données sous forme de tableau contenant la valeur de comptage des variables dans l'observation.
Exemple
Nous reprendrons les données de Cars93 dans la bibliothèque "MASS" qui représente les ventes de différents modèles de voitures en 1993.
library("MASS")
print(str(Cars93))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
'data.frame': 93 obs. of 27 variables:
$ Manufacturer : Factor w/ 32 levels "Acura","Audi",..: 1 1 2 2 3 4 4 4 4 5 ...
$ Model : Factor w/ 93 levels "100","190E","240",..: 49 56 9 1 6 24 54 74 73 35 ... $ Type : Factor w/ 6 levels "Compact","Large",..: 4 3 1 3 3 3 2 2 3 2 ...
$ Min.Price : num 12.9 29.2 25.9 30.8 23.7 14.2 19.9 22.6 26.3 33 ... $ Price : num 15.9 33.9 29.1 37.7 30 15.7 20.8 23.7 26.3 34.7 ...
$ Max.Price : num 18.8 38.7 32.3 44.6 36.2 17.3 21.7 24.9 26.3 36.3 ... $ MPG.city : int 25 18 20 19 22 22 19 16 19 16 ...
$ MPG.highway : int 31 25 26 26 30 31 28 25 27 25 ... $ AirBags : Factor w/ 3 levels "Driver & Passenger",..: 3 1 2 1 2 2 2 2 2 2 ...
$ DriveTrain : Factor w/ 3 levels "4WD","Front",..: 2 2 2 2 3 2 2 3 2 2 ... $ Cylinders : Factor w/ 6 levels "3","4","5","6",..: 2 4 4 4 2 2 4 4 4 5 ...
$ EngineSize : num 1.8 3.2 2.8 2.8 3.5 2.2 3.8 5.7 3.8 4.9 ... $ Horsepower : int 140 200 172 172 208 110 170 180 170 200 ...
$ RPM : int 6300 5500 5500 5500 5700 5200 4800 4000 4800 4100 ... $ Rev.per.mile : int 2890 2335 2280 2535 2545 2565 1570 1320 1690 1510 ...
$ Man.trans.avail : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 1 1 1 1 1 ... $ Fuel.tank.capacity: num 13.2 18 16.9 21.1 21.1 16.4 18 23 18.8 18 ...
$ Passengers : int 5 5 5 6 4 6 6 6 5 6 ... $ Length : int 177 195 180 193 186 189 200 216 198 206 ...
$ Wheelbase : int 102 115 102 106 109 105 111 116 108 114 ... $ Width : int 68 71 67 70 69 69 74 78 73 73 ...
$ Turn.circle : int 37 38 37 37 39 41 42 45 41 43 ... $ Rear.seat.room : num 26.5 30 28 31 27 28 30.5 30.5 26.5 35 ...
$ Luggage.room : int 11 15 14 17 13 16 17 21 14 18 ... $ Weight : int 2705 3560 3375 3405 3640 2880 3470 4105 3495 3620 ...
$ Origin : Factor w/ 2 levels "USA","non-USA": 2 2 2 2 2 1 1 1 1 1 ... $ Make : Factor w/ 93 levels "Acura Integra",..: 1 2 4 3 5 6 7 9 8 10 ...Le résultat ci-dessus montre que l'ensemble de données contient de nombreuses variables Factor qui peuvent être considérées comme des variables catégorielles. Pour notre modèle, nous considérerons les variables "AirBags" et "Type". Ici, nous visons à découvrir toute corrélation significative entre les types de voitures vendues et le type de sacs gonflables dont elle dispose. Si une corrélation est observée, nous pouvons estimer quels types de voitures peuvent mieux se vendre avec quels types de sacs gonflables.
# Load the library.
library("MASS")
# Create a data frame from the main data set.
car.data <- data.frame(Cars93$AirBags, Cars93$Type)
# Create a table with the needed variables.
car.data = table(Cars93$AirBags, Cars93$Type)
print(car.data)
# Perform the Chi-Square test.
print(chisq.test(car.data))Lorsque nous exécutons le code ci-dessus, cela produit le résultat suivant -
Compact Large Midsize Small Sporty Van
Driver & Passenger 2 4 7 0 3 0
Driver only 9 7 11 5 8 3
None 5 0 4 16 3 6
Pearson's Chi-squared test
data: car.data
X-squared = 33.001, df = 10, p-value = 0.0002723
Warning message:
In chisq.test(car.data) : Chi-squared approximation may be incorrectConclusion
Le résultat montre la valeur p inférieure à 0,05 qui indique une corrélation de chaîne.