Systèmes radar - Annuleurs de ligne à retard
Dans ce chapitre, nous allons découvrir les annuleurs de ligne à retard dans les systèmes radar. Comme son nom l'indique, la ligne à retard introduit un certain délai. Ainsi, la ligne à retard est principalement utilisée dans l'annuleur de ligne à retard afin d'introduire undelay du temps de répétition des impulsions.
Delay line cancellerest un filtre, qui élimine les composantes CC des signaux d'écho reçus de cibles fixes. Cela signifie qu'il autorise les composantes CA des signaux d'écho reçus de cibles non stationnaires, c'est-à-dire de cibles mobiles.
Types d'annuleurs de ligne à retard
Les annuleurs de ligne à retard peuvent être classés comme suit two types en fonction du nombre de lignes à retard qui y sont présentes.
- Annuleur de ligne à retard unique
- Annuleur de ligne à double retard
Dans nos sections suivantes, nous discuterons plus en détail de ces deux annuleurs de ligne de retard.
Annuleur de ligne à retard unique
La combinaison d'une ligne à retard et d'un soustracteur est connue sous le nom d'annuleur de ligne à retard. Il est également appelé annuleur de ligne à délai unique. leblock diagram du récepteur MTI avec annuleur de ligne à retard unique est illustré dans la figure ci-dessous.
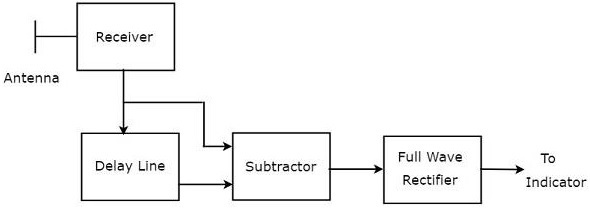
Nous pouvons écrire le mathematical equation du signal d'écho reçu après l'effet Doppler comme -
$$ V_1 = A \ sin \ left [2 \ pi f_dt- \ phi_0 \ right] \: \: \: \: \: Equation \: 1 $$
Où,
A est l'amplitude du signal vidéo
$ f_d $ est la fréquence Doppler
$ \ phi_o $ est le déphasage et il est égal à $ 4 \ pi f_tR_o / C $
Nous obtiendrons le output of Delay line canceller, en remplaçant $ t $ par $ t-T_P $ dans l'équation 1.
$$ V_2 = A \ sin \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right] \: \: \: \: \: Equation \: 2 $$
Où,
$ T_P $ est le temps de répétition de l'impulsion
Nous obtiendrons le subtractor output en soustrayant l'équation 2 de l'équation 1.
$$ V_1-V_2 = A \ sin \ left [2 \ pi f_dt- \ phi_0 \ right] -A \ sin \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right] $$
$$ \ Rightarrow V_1-V_2 = 2A \ sin \ left [\ frac {2 \ pi f_dt- \ phi_0- \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right]} {2 } \ right] \ cos \ left [\ frac {2 \ pi f_dt- \ phi_o + 2 \ pi f_d \ left (t-T_P \ right) - \ phi_0} {2} \ right] $$
$$ V_1-V_2 = 2A \ sin \ left [\ frac {2 \ pi f_dT_P} {2} \ right] \ cos \ left [\ frac {2 \ pi f_d \ left (2t-T_P \ right) -2 \ phi_0} {2} \ right] $$
$$ \ Rightarrow V_1-V_2 = 2A \ sin \ left [\ pi f_dT_p \ right] \ cos \ left [2 \ pi f_d \ left (t- \ frac {T_P} {2} \ right) - \ phi_0 \ right ] \: \: \: \: \: Équation \: 3 $$
La sortie du soustracteur est appliquée comme entrée au redresseur Full Wave. Par conséquent, la sortie de Full Wave Rectifier ressemble à celle illustrée dans la figure suivante. Ce n'est rien d'autre que lefrequency response de l'annuleur de ligne à retard unique.

À partir de l'équation 3, nous pouvons observer que la réponse en fréquence de l'annuleur de ligne à retard unique devient nulle, lorsque $ \ pi f_dT_P $ est égal à integer multiples of $ \ pi $ Cela signifie que $ \ pi f_dT_P $ est égal à $ n \ pi $ Mathématiquement, cela peut être écrit comme
$$ \ pi f_dT_P = n \ pi $$
$$ \ Rightarrow f_dT_P = n $$
$$ \ Rightarrow f_d = \ frac {n} {T_P} \: \: \: \: \: Équation \: 4 $$
À partir de l'équation 4, nous pouvons conclure que la réponse en fréquence de l'annuleur de ligne à retard unique devient nulle, lorsque la fréquence Doppler $ f_d $ est égale à des multiples entiers de l'inverse du temps de répétition d'impulsion $ T_P $.
Nous connaissons la relation suivante entre le temps de répétition des impulsions et la fréquence de répétition des impulsions.
$$ f_d = \ frac {1} {T_P} $$
$$ \ Rightarrow \ frac {1} {T_P} = f_P \: \: \: \: \: Equation \: 5 $$
Nous obtiendrons l'équation suivante, en remplaçant l'équation 5 dans l'équation 4.
$$ \ Rightarrow f_d = nf_P \: \: \: \: \: Équation \: 6 $$
À partir de l'équation 6, nous pouvons conclure que la réponse en fréquence de l'annuleur de ligne à retard unique devient nulle, lorsque la fréquence Doppler, $ f_d $ est égale à des multiples entiers de la fréquence de répétition d'impulsion $ f_P $.
Vitesses aveugles
D'après ce que nous avons appris jusqu'à présent, l'annuleur de ligne à retard unique élimine les composantes CC des signaux d'écho reçus de cibles stationnaires, lorsque $ n $ est égal à zéro. En plus de cela, il élimine également les composantes AC des signaux d'écho reçus de cibles non stationnaires, lorsque la fréquence Doppler $ f_d $ est égale à un entier(other than zero) multiples de la fréquence de répétition des impulsions $ f_P $.
Ainsi, les vitesses relatives pour lesquelles la réponse en fréquence de l'annuleur de ligne à retard unique devient nulle sont appelées blind speeds. Mathématiquement, nous pouvons écrire l'expression pour la vitesse aveugle $ v_n $ comme -
$$ v_n = \ frac {n \ lambda} {2T_P} \: \: \: \: \: Équation \: 7 $$
$$ \ Rightarrow v_n = \ frac {n \ lambda f_P} {2} \: \: \: \: \: Equation \: 8 $$
Où,
$ n $ est un entier et vaut 1, 2, 3 et ainsi de suite
$ \ lambda $ est la longueur d'onde de fonctionnement
Exemple de problème
Un radar MTI fonctionne à une fréquence de 6GHZ $ avec une fréquence de répétition des impulsions de 1KHZ $. Trouvez le premier, le deuxième et le troisièmeblind speeds de ce radar.
Solution
Donné,
La fréquence de fonctionnement du radar MTI, $ f = 6GHZ $
Fréquence de répétition des impulsions, $ f_P = 1KHZ $.
Voici la formule pour operating wavelength $ \ lambda $ en termes de fréquence de fonctionnement, f.
$$ \ lambda = \ frac {C} {f} $$
Remplacez, $ C = 3 \ times10 ^ 8m / sec $ et $ f = 6GHZ $ dans l'équation ci-dessus.
$$ \ lambda = \ frac {3 \ times10 ^ 8} {6 \ times10 ^ 9} $$
$$ \ Rightarrow \ lambda = 0,05 m $$
Alors le operating wavelength $ \ lambda $ est égal à 0,05m $, lorsque la fréquence de fonctionnement f est $ 6GHZ $.
Nous savons ce qui suit formula for blind speed.
$$ v_n = \ frac {n \ lambda f_p} {2} $$
En remplaçant, $ n $ = 1,2 & 3 dans l'équation ci-dessus, nous obtiendrons les équations suivantes pour les première, deuxième et troisième vitesses aveugles respectivement.
$$ v_1 = \ frac {1 \ times \ lambda f_p} {2} = \ frac {\ lambda f_p} {2} $$
$$ v_2 = \ frac {2 \ times \ lambda f_p} {2} = 2 \ left (\ frac {\ lambda f_p} {2} \ right) = 2v_1 $$
$$ v_3 = \ frac {3 \ times \ lambda f_p} {2} = 3 \ left (\ frac {\ lambda f_p} {2} \ right) = 3v_1 $$
Substitute les valeurs de $ \ lambda $ et $ f_P $ dans l'équation de la première vitesse aveugle.
$$ v_1 = \ frac {0,05 \ fois 10 ^ 3} {2} $$
$$ \ Flèche droite v_1 = 25 m / s $$
Par conséquent, la first blind speed $ v_1 $ est égal à 25 millions de dollars / s $ pour les spécifications données.
Nous obtiendrons les valeurs de second & third blind speeds comme $ 50m / sec $ et $ 75m / sec $ respectivement en substituant la valeur de 1 dans les équations des deuxième et troisième vitesses aveugles.
Annuleur de ligne à double retard
Nous savons qu'un seul annuleur de ligne à retard se compose d'une ligne à retard et d'un soustracteur. Si deux annuleurs de ligne à retard de ce type sont mis en cascade ensemble, alors cette combinaison est appelée annuleur de ligne à retard double. leblock diagram de l'annuleur de ligne à double retard est illustré dans la figure suivante.

Soit $ p \ left (t \ right) $ et $ q \ left (t \ right) $ l'entrée et la sortie du premier annuleur de ligne à retard. Nous obtiendrons la relation mathématique suivante à partir defirst delay line canceller.
$$ q \ gauche (t \ droite) = p \ gauche (t \ droite) -p \ gauche (t-T_P \ droite) \: \: \: \: \: Équation \: 9 $$
La sortie du premier annuleur de ligne à retard est appliquée en tant qu'entrée au second annuleur de ligne à retard. Par conséquent, $ q \ left (t \ right) $ sera l'entrée du deuxième annuleur de ligne à retard. Soit $ r \ left (t \ right) $ la sortie du deuxième annuleur de ligne à retard. Nous obtiendrons la relation mathématique suivante à partir dusecond delay line canceller.
$$ r \ left (t \ right) = q \ left (t \ right) -q \ left (t-T_P \ right) \: \: \: \: \: Équation \: 10 $$
Remplacez $ t $ par $ t-T_P $ dans l'équation 9.
$$ q \ gauche (t-T_P \ droite) = p \ gauche (t-T_P \ droite) -p \ gauche (t-T_P-T_P \ droite) $$
$$ q \ left (t-T_P \ right) = p \ left (t-T_P \ right) -p \ left (t-2T_P \ right) \: \: \: \: \: Equation \: 11 $$
Substitute, Équation 9 et équation 11 de l'équation 10.
$$ r \ gauche (t \ droite) = p \ gauche (t \ droite) -p \ gauche (t-T_P \ droite) - \ gauche [p \ gauche (t-T_P \ droite) -p \ gauche (t -2T_P \ droite) \ droite] $$
$$ \ Rightarrow r \ left (t \ right) = p \ left (t \ right) -2p \ left (t-T_P \ right) + p \ left (t-2T_P \ right) \: \: \: \ : \: Équation \: 12 $$
le advantagede l'annuleur de ligne à retard double est qu'il rejette largement le fouillis. La sortie de deux annuleurs de ligne à retard, qui sont en cascade, sera égale au carré de la sortie de l'annuleur de ligne à retard unique.
Ainsi, la magnitude de sortie du double annuleur de ligne à retard, qui est présent au récepteur radar MTI, sera égale à $ 4A ^ 2 \ left (\ sin \ left [\ pi f_dT_P \ right] \ right) ^ 2 $.

Les caractéristiques de réponse en fréquence du double annuleur de ligne à retard et de la combinaison en cascade de deux annuleurs de ligne à retard sont les mêmes. leadvantage de l'annuleur de ligne à retard dans le domaine temporel est qu'il peut être utilisé pour toutes les plages de fréquences.