Systèmes radar - Guide rapide
RADAR est un système de détection électromagnétique qui fonctionne en rayonnant des ondes électromagnétiques puis en étudiant l'écho ou les ondes réfléchies.
La forme complète de RADAR est RAdio Detection And Rla colère. La détection fait référence à la présence ou non de la cible. La cible peut être fixe ou mobile, c'est-à-dire non stationnaire. La distance fait référence à la distance entre le radar et la cible.
Les radars peuvent être utilisés pour diverses applications au sol, en mer et dans l'espace. leapplications des radars sont répertoriés ci-dessous.
- Contrôle du trafic aérien
- Sécurité des navires
- Détecter les endroits éloignés
- Applications militaires
Dans toute application de Radar, le principe de base reste le même. Parlons maintenant du principe du radar.
Principe de base du radar
Le radar est utilisé pour détecter les objets et trouver leur emplacement. Nous pouvons comprendre lebasic principle du radar à partir de la figure suivante.

Comme le montre la figure, le radar se compose principalement d'un émetteur et d'un récepteur. Il utilise la même antenne pour transmettre et recevoir les signaux. La fonction dutransmitter est de transmettre le signal radar en direction de la cible présente.
La cible reflète ce signal reçu dans diverses directions. Le signal, qui est réfléchi vers l'antenne est reçu par lereceiver.
Terminologie des systèmes radar
Voici les termes de base, qui sont utiles dans ce didacticiel.
- Range
- Fréquence de répétition des impulsions
- Portée maximale non ambiguë
- Gamme minimale
Maintenant, laissez-nous discuter de ces termes de base un par un.
Intervalle
La distance entre le radar et la cible est appelée Range de la cible ou simplement de la distance, R. Nous savons que le radar transmet un signal à la cible et en conséquence la cible envoie un signal d'écho au radar avec la vitesse de la lumière, C.
Soit «T» le temps nécessaire au signal pour se déplacer du radar à la cible et revenir au radar. La distance bidirectionnelle entre le radar et la cible sera 2R, puisque la distance entre le radar et la cible est R.
Maintenant, voici la formule pour Speed.
$$Speed= \frac{Distance}{Time}$$
$$\Rightarrow Distance=Speed\times Time$$
$$\Rightarrow 2R=C\times T$$
$$R=\frac{CT}{2}\:\:\:\:\:Equation\:1$$
Nous pouvons trouver le range of the target en remplaçant les valeurs de C et T dans l'équation 1.
Fréquence de répétition des impulsions
Les signaux radar doivent être transmis à chaque impulsion d'horloge. La durée entre les deux impulsions d'horloge doit être convenablement choisie de manière à ce que le signal d'écho correspondant à l'impulsion d'horloge actuelle soit reçu avant l'impulsion d'horloge suivante. Un typiqueRadar wave form est illustré dans la figure suivante.

Comme le montre la figure, le radar émet un signal périodique. Il a une série d'impulsions étroites de forme rectangulaire. L'intervalle de temps entre les impulsions d'horloge successives est appelépulse repetition time, $T_P$.
L'inverse du temps de répétition des impulsions est appelé pulse repetition frequency, $f_P$. Mathématiquement, il peut être représenté comme
$$f_P=\frac{1}{T_P}\:\:\:\:\:Equation\:2$$Par conséquent, la fréquence de répétition des impulsions n'est rien d'autre que la fréquence à laquelle le radar transmet le signal.
Portée maximale non ambiguë
Nous savons que les signaux radar doivent être transmis à chaque impulsion d'horloge. Si nous sélectionnons une durée plus courte entre les deux impulsions d'horloge, alors le signal d'écho correspondant à l'impulsion d'horloge actuelle sera reçu après l'impulsion d'horloge suivante. Pour cette raison, la portée de la cible semble être plus petite que la portée réelle.
Ainsi, nous devons sélectionner la durée entre les deux impulsions d'horloge de telle sorte que le signal d'écho correspondant à l'impulsion d'horloge actuelle soit reçu avant le début de l'impulsion d'horloge suivante. Ensuite, nous obtiendrons la vraie portée de la cible et on l'appelle aussi portée maximale non ambiguë de la cible ou simplement,maximum unambiguous range.
Remplacer, $R=R_{un}$ et $T=T_P$ dans l'équation 1.
$$R_{un}=\frac{CT_P}{2}\:\:\:\:\:Equation\:3$$
À partir de l'équation 2, nous obtiendrons le temps de répétition des impulsions, $T_P$ comme réciproque de la fréquence de répétition des impulsions, $f_P$. Mathematically, il peut être représenté comme
$$T_P=\frac{1}{f_P}\:\:\:\:\:Equation\:4$$
Substitut, équation 4 dans l'équation 3.
$$R_{un}=\frac{C\left ( \frac{1}{f_P} \right )}{2}$$
$$R_{un}=\frac{C}{2f_P}\:\:\:\:\:Equation\:5$$
Nous pouvons utiliser l'équation 3 ou l'équation 5 pour calculer la plage maximale non ambiguë de la cible.
Nous obtiendrons la valeur de la plage maximale non ambiguë de la cible, $R_{un}$ en substituant les valeurs de $C$ et $T_P$ dans l'équation 3.
De même, nous obtiendrons la valeur de la plage maximale non ambiguë de la cible, $R_{un}$ en substituant les valeurs de $C$ et $f_P$ dans l'équation 5.
Gamme minimale
Nous obtiendrons le minimum rangede la cible, lorsque nous considérons le temps nécessaire pour que le signal d'écho reçoive au radar après le signal transmis par le radar comme largeur d'impulsion. On l'appelle également la portée la plus courte de la cible.
Remplacer, $R=R_{min}$ et $T=\tau$ dans l'équation 1.
$$R_{min}=\frac{C\tau}{2}\:\:\:\:\:Equation\:6$$
Nous obtiendrons la valeur de la portée minimale de la cible, $R_{min}$ en substituant les valeurs de $C$ et $\tau$ dans l'équation 6.
L'équation de distance radar est utile pour connaître la portée de la cible theoretically. Dans ce chapitre, nous discuterons de la forme standard de l'équation de distance radar, puis nous discuterons des deux formes modifiées de l'équation de distance radar.
Nous obtiendrons ces formes modifiées de l'équation de distance radar à partir de la forme standard de l'équation de distance radar. Maintenant, laissez-nous discuter de la dérivation de la forme standard de l'équation de distance radar.
Dérivation de l'équation de portée radar
La forme standard de l'équation de distance radar est également appelée forme simple d'équation de distance radar. Maintenant, dérivons la forme standard de l'équation de distance radar.
Nous savons que power densityn'est rien d'autre que le rapport puissance / surface. Donc, la densité de puissance,$P_{di}$ à distance, R du radar peut être représenté mathématiquement par -
$$P_{di}=\frac{P_t}{4\pi R^2}\:\:\:\:\:Equation\:1$$
Où,
$P_t$La densité de puissance ci-dessus est valable pour une antenne isotrope. En général, les radars utilisent des antennes directionnelles. Par conséquent, la densité de puissance,$P_{dd}$ en raison de l'antenne directionnelle sera -
$$P_{dd}=\frac{P_tG}{4\pi R^2}\:\:\:\:\:Equation\:2$$
La cible rayonne la puissance dans différentes directions à partir de la puissance d'entrée reçue. La quantité de puissance réfléchie vers le radar dépend de sa section transversale. Donc, la densité de puissance$P_{de}$ du signal d'écho au radar peut être représenté mathématiquement par -
$$P_{de}=P_{dd}\left (\frac{\sigma}{4\pi R^2}\right )\:\:\:\:\:Equation\:3$$ Substitut, équation 2 dans l'équation 3.
$$P_{de}=\left (\frac{P_tG}{4\pi R^2}\right )\left (\frac{\sigma}{4\pi R^2}\right )\:\:\:\:\:Equation\:4$$
La quantité de power, $P_r$ received par le radar dépend de l'ouverture effective, $A_e$ de l'antenne de réception.
$$P_r=P_{de}A_e\:\:\:\:\:Equation\:5$$
Substitut, équation 4 dans l'équation 5.
$$P_r=\left (\frac{P_tG}{4\pi R^2}\right )\left (\frac{\sigma}{4\pi R^2}\right )A_e$$
$$\Rightarrow P_r=\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 R^4}$$
$$\Rightarrow R^4=\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 P_r}$$
$$\Rightarrow R=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 P_r}\right ]^{1/4}\:\:\:\:\:Equation\:6$$
Forme standard de l'équation de portée radar
Si le signal d'écho a une puissance inférieure à la puissance du signal détectable minimum, alors le radar ne peut pas détecter la cible car elle est au-delà de la limite maximale de la portée du radar.
Par conséquent, on peut dire que la portée de la cible est dite portée maximale lorsque le signal d'écho reçu a la puissance égale à celle du signal détectable minimum. Nous obtiendrons l'équation suivante, en remplaçant$R=R_{Max}$ et $P_r=S_{min}$ dans l'équation 6.
$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}\:\:\:\:\:Equation\:7$$
L'équation 7 représente le standard formde l'équation de portée radar. En utilisant l'équation ci-dessus, nous pouvons trouver la portée maximale de la cible.
Formes modifiées de l'équation de portée radar
Nous connaissons la relation suivante entre le gain de l'antenne directionnelle, $G$ et ouverture effective, $A_e$.
$$G=\frac{4\pi A_e}{\lambda^2}\:\:\:\:\:Equation\:8$$
Substitut, équation 8 dans l'équation 7.
$$R_{Max}=\left [ \frac{P_t\sigma A_e}{\left ( 4\pi \right )^2S_{min}}\left ( \frac{4\pi A_e}{\lambda^2} \right ) \right ]^{1/4}$$
$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma {A_e}^2}{4\pi \lambda^2 S_{min}}\right ]^{1/4}\:\:\:\:\:Equation\:9$$
L'équation 9 représente le modified formde l'équation de portée radar. En utilisant l'équation ci-dessus, nous pouvons trouver la portée maximale de la cible.
Nous obtiendrons la relation suivante entre l'ouverture effective, $A_e$ et le gain de l'antenne directionnelle, $G$ de l'équation 8.
$$A_e=\frac{G\lambda^2}{4\pi}\:\:\:\:\:Equation\:10$$
Substitut, équation 10 dans l'équation 7.
$$R_{Max}=\left [\frac{P_tG\sigma}{\left (4\pi\right )^2 S_{min}}(\frac{G\lambda^2}{4\pi})\right ]^{1/4}$$
$$\Rightarrow R_{Max}=\left [\frac{P_tG^2 \lambda^2 \sigma}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}\:\:\:\:\:Equation\:11$$
L'équation 11 représente another modified form de l'équation de portée radar. En utilisant l'équation ci-dessus, nous pouvons trouver la portée maximale de la cible.
Note - Sur la base des données données, nous pouvons trouver la portée maximale de la cible en utilisant l'une de ces trois équations à savoir
- Équation 7
- Équation 9
- Équation 11
Exemples de problèmes
Dans la section précédente, nous avons obtenu les formes standard et modifiées de l'équation de portée radar. Maintenant, résolvons quelques problèmes en utilisant ces équations.
Problème 1
Calculez le maximum range of Radar pour les spécifications suivantes -
- Puissance de crête transmise par le radar, $P_t=250KW$
- Gain d'antenne émettrice, $G=4000$
- Ouverture effective de l'antenne de réception, $A_e=4\:m^2$
- Coupe transversale radar de la cible, $\sigma=25\:m^2$
- Puissance du signal détectable minimum, $S_{min}=10^{-12}W$
Solution
Nous pouvons utiliser ce qui suit standard form de l'équation de portée radar afin de calculer la portée maximale du radar pour des spécifications données.
$$R_{Max}=\left [\frac{P_tG \sigma A_e}{\left (4\pi \right )^2 S_{min}}\right ]^{1/4}$$
Substitute tous les paramètres donnés dans l'équation ci-dessus.
$$R_{Max}=\left [\frac{ \left ( 250\times 10^3 \right )\left ( 4000 \right )\left ( 25 \right )\left ( 4 \right )}{\left ( 4\pi \right )^2 \left ( 10^{-12} \right )} \right ]^{1/4}$$
$$\Rightarrow R_{Max}=158\:KM$$
Par conséquent, la maximum range of Radar pour des spécifications données est $158\:KM$.
Problème 2
Calculez le maximum range of Radar pour les spécifications suivantes.
- Fréquence de fonctionnement, $f=10GHZ$
- Puissance de crête transmise par le radar, $P_t=400KW$
- Ouverture effective de l'antenne de réception, $A_e=5\:m^2$
- Coupe transversale radar de la cible, $\sigma=30\:m^2$
- Puissance du signal détectable minimum, $S_{min}=10^{-10}W$
Solution
Nous connaissons la formule suivante pour operating wavelength, $\lambda$ en termes de fréquence de fonctionnement, f.
$$\lambda =\frac{C}{f}$$
Remplacer, $C=3\times 10^8m/sec$ et $f=10GHZ$ dans l'équation ci-dessus.
$$\lambda =\frac{3\times 10^8}{10\times 10^9}$$
$$\Rightarrow \lambda=0.03m$$
Alors le operating wavelength,$\lambda$ est égal à $0.03m$, lorsque la fréquence de fonctionnement, $f$ est $10GHZ$.
Nous pouvons utiliser ce qui suit modified form de l'équation de portée radar afin de calculer la portée maximale du radar pour des spécifications données.
$$R_{Max}=\left [\frac{P_t \sigma {A_e}^2}{4\pi \lambda^2 S_{min}}\right ]^{1/4}$$
Substitute, les paramètres donnés dans l'équation ci-dessus.
$$R_{Max}=\left [ \frac{\left ( 400\times 10^3 \right )\left ( 30 \right )\left ( 5^2 \right )}{4\pi\left ( 0.003 \right )^2\left ( 10 \right )^{-10}} \right ]^{1/4}$$
$$\Rightarrow R_{Max}=128KM$$
Par conséquent, la maximum range of Radar pour des spécifications données est $128\:KM$.
Les facteurs qui affectent les performances du radar sont appelés facteurs de performance du radar. Dans ce chapitre, discutons de ces facteurs. Nous savons que ce qui suitstandard form de l'équation de distance radar, qui est utile pour calculer la portée maximale du radar pour des spécifications données.
$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$
Où,
$P_t$ est la puissance de crête transmise par le radar
$G$ est le gain de l'antenne de transmission
$\sigma$ est la section transversale radar de la cible
$A_e$ est l'ouverture effective de l'antenne de réception
$S_{min}$ est la puissance du signal détectable minimum
À partir de l'équation ci-dessus, nous pouvons conclure que ce qui suit conditions doit être pris en compte pour obtenir la portée maximale du radar.
- Puissance de crête transmise par le radar $P_t$ devrait être élevé.
- Gain de l'antenne émettrice $G$ devrait être élevé.
- Coupe transversale radar de la cible $\sigma$ devrait être élevé.
- Ouverture effective de l'antenne de réception $A_e$ devrait être élevé.
- Puissance du signal détectable minimum $S_{min}$ devrait être faible.
Il est difficile de prédire la portée de la cible à partir de la forme standard de l'équation de portée radar. Cela signifie que le degré de précision fourni par l'équation de distance radar sur la distance de la cible est moindre. Parce que les paramètres tels que la section transversale radar de la cible,$\sigma$ et signal détectable minimum, $S_{min}$ sont statistical in nature.
Signal détectable minimum
Si le signal d'écho a une puissance minimale, la détection de ce signal par le radar est appelée minimum detectable signal. Cela signifie que le radar ne peut pas détecter le signal d'écho si ce signal a une puissance inférieure à celle de la puissance minimale.
En général, le radar reçoit le signal d'écho en plus du bruit. Si la valeur de seuil est utilisée pour détecter la présence de la cible à partir du signal reçu, alors cette détection est appeléethreshold detection.
Nous devons sélectionner la valeur de seuil appropriée en fonction de la force du signal à détecter.
Une valeur de seuil élevée doit être choisie lorsque la force du signal à détecter est élevée afin d'éliminer le signal de bruit indésirable qui y est présent.
De même, une valeur de seuil basse doit être choisie lorsque la force du signal à détecter est faible.
Le suivant figure illustre ce concept -

UNE typical waveformdu récepteur radar est illustré dans la figure ci-dessus. L'axe des x et l'axe des y représentent respectivement le temps et la tension. La valeur efficace du bruit et la valeur seuil sont indiquées par des lignes pointillées dans la figure ci-dessus.
Nous avons considéré trois points, A, B et C dans la figure ci-dessus pour identifier les détections valides et les détections manquantes.
La valeur du signal au point A est supérieure à la valeur seuil. Par conséquent, c'est unvalid detection.
La valeur du signal au point B est égale à la valeur seuil. Par conséquent, c'est unvalid detection.
Même si la valeur du signal au point C est plus proche de la valeur seuil, c'est un missing detection. Parce que la valeur du signal au point C est inférieure à la valeur seuil.
Ainsi, les points, A et B sont des détections valides. Alors que le point C est une détection manquante.
Bruit du récepteur
Si le récepteur génère une composante de bruit dans le signal, qui est reçu au niveau du récepteur, alors ce type de bruit est appelé bruit du récepteur. lereceiver noiseest un composant indésirable; nous devrions essayer de l'éliminer avec quelques précautions.
Cependant, il existe un type de bruit connu sous le nom de bruit thermique. Cela se produit en raison du mouvement thermique des électrons de conduction. Mathématiquement, on peut écrirethermal noise power, $N_i$ produit au récepteur comme -
$$N_i=KT_oB_n$$
Où,
$K$ est la constante de Boltzmann et elle est égale à $1.38\times 10^{-23}J/deg$
$T_o$ est la température absolue et elle est égale à $290^0K$
$B_n$ est la largeur de bande du récepteur
Symbole de mérite
le Figure of Merit, F n'est rien d'autre que le rapport du SNR d'entrée, $(SNR)_i$ et sortie SNR, $(SNR)_o$. Mathématiquement, il peut être représenté par -
$$F=\frac{(SNR)_i}{(SNR)_o}$$
$$\Rightarrow F=\frac{S_i/N_i}{S_o/N_o}$$
$$\Rightarrow F=\frac{N_oS_i}{N_iS_o}$$
$$\Rightarrow S_i=\frac{FN_iS_o}{N_o}$$
Remplacer, $N_i=KT_oB_n$ dans l'équation ci-dessus.
$$\Rightarrow S_i=FKT_oB_n\left ( \frac{S_o}{N_o}\right )$$
La puissance du signal d'entrée aura une valeur minimale, lorsque le SNR de sortie aura une valeur minimale.
$$\Rightarrow S_{min}=FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}$$
Remplaçant, ce qui précède $S_{min}$ sous la forme standard suivante de l'équation de portée radar.
$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$
$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}}\right ]^{1/4}$$
À partir de l'équation ci-dessus, nous pouvons conclure que ce qui suit conditions doit être pris en compte pour obtenir la portée maximale du radar.
- Puissance de crête transmise par le radar, $P_t$ devrait être élevé.
- Gain de l'antenne émettrice $G$ devrait être élevé.
- Coupe transversale radar de la cible $\sigma$ devrait être élevé.
- Ouverture effective de l'antenne de réception $A_e$ devrait être élevé.
- La valeur du mérite F doit être faible.
- Bande passante du récepteur $B_n$ devrait être faible.
Dans ce chapitre, nous aborderons brièvement les différents types de radar. Ce chapitre fournit des informations succinctes sur les types de radars. Les radars peuvent être classés comme suittwo types en fonction du type de signal avec lequel le radar peut être utilisé.
- Radar à impulsions
- Radar à ondes continues
Maintenant, laissez-nous discuter de ces deux types de radars un par un.
Radar à impulsions
Le radar, qui fonctionne avec un signal d'impulsion est appelé le Pulse Radar. Les radars à impulsions peuvent être classés dans les deux types suivants en fonction du type de cible détecté.
- Radar à impulsions de base
- Radar d'indication de cible mobile
Parlons maintenant brièvement des deux radars.
Radar à impulsions de base
Le radar, qui fonctionne avec un signal d'impulsion pour détecter des cibles stationnaires, est appelé le Basic Pulse Radarou simplement, Pulse Radar. Il utilise une seule antenne pour transmettre et recevoir des signaux à l'aide du duplexeur.
L'antenne transmettra un signal d'impulsion à chaque impulsion d'horloge. La durée entre les deux impulsions d'horloge doit être choisie de manière à ce que le signal d'écho correspondant à l'impulsion d'horloge actuelle soit reçu avant l'impulsion d'horloge suivante.
Radar d'indication de cible mobile
Le radar, qui fonctionne avec un signal d'impulsion pour détecter des cibles non stationnaires, est appelé Radar d'indication de cible mobile ou simplement, MTI Radar. Il utilise une seule antenne pour la transmission et la réception de signaux à l'aide du duplexeur.
MTI Radar utilise le principe de Doppler effect pour distinguer les cibles non stationnaires des objets stationnaires.
Radar à ondes continues
Le radar, qui fonctionne avec un signal ou une onde continue est appelé Continuous Wave Radar. Ils utilisent l'effet Doppler pour détecter des cibles non stationnaires. Les radars à ondes continues peuvent être classés dans les deux types suivants.
- Radar à ondes continues non modulé
- Radar à ondes continues à modulation de fréquence
Maintenant, parlons brièvement des deux radars.
Radar à ondes continues non modulé
Le radar, qui fonctionne avec un signal continu (onde) pour détecter des cibles non stationnaires est appelé radar à ondes continues non modulé ou simplement, CW Radar. Il est également appelé radar Doppler CW.
Ce radar nécessite deux antennes. Parmi ces deux antennes, une antenne est utilisée pour transmettre le signal et l'autre antenne est utilisée pour recevoir le signal. Il ne mesure que la vitesse de la cible mais pas la distance entre la cible et le radar.
Radar à ondes continues à modulation de fréquence
Si le radar Doppler CW utilise la modulation de fréquence, alors ce radar est appelé onde continue modulée en fréquence (FMCW)Radar ou radar Doppler FMCW. Il est également appelé radar à modulation de fréquence à ondes continues ou radar CWFM.
Ce radar nécessite deux antennes. Parmi lesquelles, une antenne est utilisée pour transmettre le signal et l'autre antenne est utilisée pour recevoir le signal. Il mesure non seulement la vitesse de la cible, mais également la distance de la cible par rapport au radar.
Dans nos chapitres suivants, nous discuterons en détail du fonctionnement de tous ces radars.
Le radar, qui fonctionne avec un signal d'impulsion pour détecter des cibles stationnaires est appelé Radar à impulsions de base ou simplement, Pulse Radar. Dans ce chapitre, parlons du fonctionnement de Pulse Radar.
Schéma fonctionnel du radar à impulsions
Pulse Radar utilise une seule antenne pour la transmission et la réception de signaux à l'aide du duplexeur. Voici leblock diagram du radar à impulsions -

Voyons maintenant le function de chaque bloc de Pulse Radar -
Pulse Modulator - Il produit un signal modulé par impulsions et il est appliqué à l'émetteur.
Transmitter - Il transmet le signal modulé par impulsions, qui est un train d'impulsions répétitives.
Duplexer- Il s'agit d'un commutateur micro-ondes, qui relie alternativement l'antenne à la section émetteur et à la section récepteur. L'antenne transmet le signal modulé par impulsions, lorsque le duplexeur connecte l'antenne à l'émetteur. De même, le signal, qui est reçu par l'antenne sera donné à l'amplificateur RF à faible bruit, lorsque le duplexeur connecte l'antenne à l'amplificateur RF à faible bruit.
Low Noise RF Amplifier- Il amplifie le faible signal RF, qui est reçu par l'antenne. La sortie de cet amplificateur est connectée au mélangeur.
Local Oscillator- Il produit un signal ayant une fréquence stable. La sortie de l'oscillateur local est connectée au mélangeur.
Mixer- Nous savons que Mixer peut produire à la fois la somme et la différence des fréquences qui lui sont appliquées. Parmi lesquels, la différence des fréquences sera de type Fréquence Intermédiaire (IF).
IF Amplifier- L'amplificateur IF amplifie le signal de fréquence intermédiaire (IF). L'amplificateur IF illustré sur la figure n'autorise que la fréquence intermédiaire, qui est obtenue à partir du mélangeur et l'amplifie. Il améliore le rapport signal / bruit en sortie.
Detector - Il démodule le signal, qui est obtenu à la sortie de l'amplificateur IF.
Video Amplifier - Comme son nom l'indique, il amplifie le signal vidéo, qui est obtenu à la sortie du détecteur.
Display - En général, il affiche le signal vidéo amplifié sur l'écran CRT.
Dans ce chapitre, nous avons discuté du fonctionnement du radar à impulsions et de son utilité pour détecter des cibles stationnaires. Dans nos chapitres suivants, nous discuterons des radars, qui sont utiles pour détecter des cibles non stationnaires.
Dans ce chapitre, nous allons en apprendre davantage sur l'effet Doppler dans les systèmes radar.
Si la cible n'est pas stationnaire, alors il y aura un changement dans la fréquence du signal qui est émis par le radar et qui est reçu par le radar. Cet effet est connu sous le nom deDoppler effect.
Selon l'effet Doppler, nous obtiendrons les deux cas possibles suivants -
le frequency du signal reçu sera increase, lorsque la cible se déplace vers la direction du radar.
le frequency du signal reçu sera decrease, lorsque la cible s'éloigne du radar.
Maintenant, dérivons la formule de la fréquence Doppler.
Dérivation de la fréquence Doppler
La distance entre le radar et la cible n'est rien d'autre que Range de la cible ou simplement de la distance, R. Par conséquent, la distance totale entre le radar et la cible dans une voie de communication bidirectionnelle sera 2R, puisque le radar transmet un signal à la cible et en conséquence la cible envoie un signal d'écho au radar.
Si $\lambda$ est une longueur d'onde, alors le nombre de longueurs d'onde N présentes dans un chemin de communication bidirectionnel entre le radar et la cible sera égal à $2R/\lambda$.
Nous savons qu'une longueur d'onde $\lambda$ correspond à une excursion angulaire de $2\pi$radians. Alors letotal angle of excursion fait par l'onde électromagnétique pendant le chemin de communication bidirectionnel entre le radar et la cible sera égal à $4\pi R/\lambda$ radians.
Voici la formule mathématique pour angular frequency, $\omega$ -
$$\omega=2\pi f\:\:\:\:\:Equation\:1$$
L'équation suivante montre la relation mathématique entre la fréquence angulaire $\omega$ et angle de phase $\phi$ -
$$\omega=\frac{d\phi }{dt}\:\:\:\:\:Equation\:2$$
Equate les termes du côté droit de l'équation 1 et de l'équation 2 puisque les termes du côté gauche de ces deux équations sont identiques.
$$2\pi f=\frac{d\phi }{dt}$$
$$\Rightarrow f =\frac{1}{2\pi}\frac{d\phi }{dt}\:\:\:\:\:Equation\:3$$
Substitute,$f=f_d$ et $\phi=4\pi R/\lambda$ dans l'équation 3.
$$f_d =\frac{1}{2\pi}\frac{d}{dt}\left ( \frac{4\pi R}{\lambda} \right )$$
$$\Rightarrow f_d =\frac{1}{2\pi}\frac{4\pi}{\lambda}\frac{dR}{dt}$$
$$\Rightarrow f_d =\frac{2V_r}{\lambda}\:\:\:\:\:Equation\:4$$
Où,
$f_d$ est la fréquence Doppler
$V_r$ est la vitesse relative
Nous pouvons trouver la valeur de la fréquence Doppler $f_d$ en substituant les valeurs de $V_r$ et $\lambda$ dans l'équation 4.
Substitute, $\lambda=C/f$ dans l'équation 4.
$$f_d =\frac{2V_r}{C/f}$$
$$\Rightarrow f_d =\frac{2V_rf}{C}\:\:\:\:\:Equation\:5$$
Où,
$f$ est la fréquence du signal émis
$C$ est la vitesse de la lumière et elle est égale à $3\times 10^8m/sec$
On peut trouver la valeur de la fréquence Doppler, $f_d$ en substituant les valeurs de $V_r,f$ et $C$ dans l'équation 5.
Note - L'équation 4 et l'équation 5 montrent les formules de la fréquence Doppler, $f_d$. Nous pouvons utiliser l'équation 4 ou l'équation 5 pour trouverDoppler frequency, $f_d$ basé sur les données fournies.
Exemple de problème
Si le radar fonctionne à une fréquence de $5GHZ$, puis trouvez le Doppler frequency d'un avion se déplaçant à une vitesse de 100 km / h.
Solution
Donné,
La fréquence du signal transmis, $f=5GHZ$
Vitesse de l'avion (cible), $V_r=100KMph$
$$\Rightarrow V_r=\frac{100\times 10^3}{3600}m/sec$$
$$\Rightarrow V_r=27.78m/sec$$
Nous avons converti la vitesse donnée de l'avion (cible), qui est présente en KMph en son équivalent m / s.
Nous savons que, la vitesse de la lumière, $C=3\times 10^8m/sec$
Maintenant, voici le formula for Doppler frequency -
$$f_d=\frac{2Vrf}{C}$$
Substitute les valeurs de ð ?? '‰ ð ??' Ÿ, $V_r,f$ et $C$ dans l'équation ci-dessus.
$$\Rightarrow f_d=\frac{2\left ( 27.78 \right )\left ( 5\times 10^9 \right )}{3\times 10^8}$$
$$\Rightarrow f_d=926HZ$$
Par conséquent, la valeur de Doppler frequency, $f_d$ est $926HZ$ pour les spécifications données.
Le radar de base utilise la même antenne pour la transmission et la réception des signaux. Nous pouvons utiliser ce type de radar, lorsque la cible est stationnaire, c'est-à-dire immobile et / ou lorsque ce radar peut être utilisé avec un signal d'impulsion.
Le radar, qui fonctionne avec un signal continu (onde) pour détecter des cibles non stationnaires, est appelé Radar à ondes continues ou simplement CW Radar. Ce radar nécessite deux antennes. Parmi lesquelles, une antenne est utilisée pour transmettre le signal et l'autre antenne est utilisée pour recevoir le signal.
Schéma fonctionnel du radar CW
Nous savons que le radar Doppler CW contient deux antennes - l'antenne d'émission et l'antenne de réception. La figure suivante montre leblock diagram du radar CW -

Le schéma fonctionnel du radar Doppler CW contient un ensemble de blocs et le function de chaque bloc est mentionné ci-dessous.
CW Transmitter - Il produit un signal analogique ayant une fréquence de $f_o$. La sortie de l'émetteur CW est connectée à la fois à l'antenne de transmission et au mélangeur-I.
Local Oscillator - Il produit un signal ayant une fréquence de $f_l$. La sortie de l'oscillateur local est connectée à Mixer-I.
Mixer-I- Le mélangeur peut produire à la fois la somme et la différence des fréquences qui lui sont appliquées. Les signaux ayant des fréquences de$f_o$ et $f_l$sont appliqués à Mixer-I. Ainsi, le Mixer-I produira la sortie ayant des fréquences$f_o+f_l$ ou $f_o−f_l$.
Side Band Filter- Comme son nom l'indique, le filtre à bande latérale autorise des fréquences de bande latérale particulières - soit des fréquences de bande latérale supérieure, soit des fréquences de bande latérale inférieure. Le filtre de bande latérale représenté sur la figure ci-dessus ne produit que la fréquence de bande latérale supérieure, c'est-à-dire$f_o+f_l$.
Mixer-II- Le mélangeur peut produire à la fois la somme et la différence des fréquences qui lui sont appliquées. Les signaux ayant des fréquences de$f_o+f_l$ et $f_o\pm f_d$sont appliqués à Mixer-II. Ainsi, le Mixer-II produira la sortie avec des fréquences de 2$f_o+f_l\pm f_d$ ou $f_l\pm f_d$.
IF Amplifier- L'amplificateur IF amplifie le signal de fréquence intermédiaire (IF). L'amplificateur IF illustré sur la figure autorise uniquement la fréquence intermédiaire,$f_l\pm f_d$ et l'amplifie.
Detector - Il détecte le signal, qui a une fréquence Doppler, $f_d$.
Doppler Amplifier - Comme son nom l'indique, l'amplificateur Doppler amplifie le signal, qui a une fréquence Doppler, $f_d$.
Indicator - Il indique la vitesse relative relative aux informations et si la cible est entrante ou sortante.
Les radars Doppler CW donnent une mesure précise de relative velocities. Par conséquent, ceux-ci sont principalement utilisés, où les informations de vitesse sont plus importantes que la plage réelle.
Si le radar Doppler CW utilise la modulation de fréquence, alors ce radar est appelé FMCW Doppler Radar ou simplement, FMCW Radar. Il est également appelé radar à modulation de fréquence à ondes continues ou radar CWFM. Il mesure non seulement la vitesse de la cible, mais également la distance de la cible par rapport au radar.
Schéma fonctionnel du radar FMCW
Le radar FMCW est principalement utilisé comme altimètre radar afin de mesurer la hauteur exacte lors de l'atterrissage de l'avion. La figure suivante montre leblock diagram du radar FMCW -

FMCW Radarcontient deux antennes - une antenne de transmission et une antenne de réception comme indiqué sur la figure. L'antenne émettrice transmet le signal et l'antenne réceptrice reçoit le signal d'écho.
Le schéma de principe du radar FMCW ressemble au schéma de principe du radar CW. Il contient quelques blocs modifiés et quelques autres blocs en plus des blocs qui sont présents dans le diagramme de CW Radar. lefunction de chaque bloc de radar FMCW est mentionné ci-dessous.
FM Modulator - Il produit un signal à modulation de fréquence (FM) à fréquence variable, $f_o\left (t \right )$ et il est appliqué à l'émetteur FM.
FM Transmitter- Il transmet le signal FM à l'aide de l'antenne de transmission. La sortie de l'émetteur FM est également connectée à Mixer-I.
Local Oscillator- En général, l'Oscillateur Local est utilisé pour produire un signal RF. Mais, ici, il est utilisé pour produire un signal ayant une fréquence intermédiaire,$f_{IF}$. La sortie de l'Oscillateur Local est connectée à la fois au Mixer-I et au Détecteur équilibré.
Mixer-I- Le mélangeur peut produire à la fois la somme et la différence des fréquences qui lui sont appliquées. Les signaux ayant des fréquences de$f_o\left (t \right )$ et $f_{IF}$sont appliqués à Mixer-I. Ainsi, le Mixer-I produira la sortie ayant une fréquence soit$f_o\left (t \right )+f_{IF}$ ou $f_o\left (t \right )-f_{IF}$.
Side Band Filter- Il n'autorise qu'une seule bande latérale de fréquences, c'est-à-dire des fréquences de bande latérale supérieure ou des fréquences de bande latérale inférieure. Le filtre de bande latérale représenté sur la figure produit uniquement une fréquence de bande latérale inférieure. c'est à dire,$f_o\left (t \right )-f_{IF}$.
Mixer-II- Le mélangeur peut produire à la fois la somme et la différence des fréquences qui lui sont appliquées. Les signaux ayant des fréquences de$f_o\left (t \right )-f_{IF}$ et $f_o\left (t-T \right )$sont appliqués à Mixer-II. Ainsi, le Mixer-II produira la sortie ayant une fréquence soit$f_o\left (t-T \right )+f_o\left (t \right )-f_{IF}$ ou $f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$.
IF Amplifier- L'amplificateur IF amplifie le signal de fréquence intermédiaire (IF). L'amplificateur IF illustré sur la figure amplifie le signal ayant une fréquence de$f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$. Ce signal amplifié est appliqué en tant qu'entrée au détecteur équilibré.
Balanced Detector - Il est utilisé pour produire le signal de sortie ayant une fréquence de $f_o\left (t-T \right )-f_o\left (t \right )$ à partir des deux signaux d'entrée appliqués, qui ont des fréquences de $f_o\left (t-T \right )-f_o\left (t \right )+f_{IF}$ et $f_{IF}$. La sortie du détecteur équilibré est appliquée en tant qu'entrée à l'amplificateur basse fréquence.
Low Frequency Amplifier- Il amplifie la sortie du détecteur équilibré au niveau requis. La sortie de l'amplificateur basse fréquence est appliquée à la fois au compteur de fréquence commuté et au compteur de fréquence moyenne.
Switched Frequency Counter - Il est utile pour obtenir la valeur de la vitesse Doppler.
Average Frequency Counter - Il est utile pour obtenir la valeur de Range.
Si le radar est utilisé pour détecter la cible mobile, alors le radar ne devrait recevoir que le signal d'écho dû à cette cible mobile. Ce signal d'écho est celui souhaité. Cependant, dans les applications pratiques, le radar reçoit les signaux d'écho dus aux objets stationnaires en plus du signal d'écho dû à cette cible mobile.
Les signaux d'écho dus à des objets fixes (lieux) tels que la terre et la mer sont appelés cluttersparce que ce sont des signaux indésirables. Par conséquent, nous devons choisir le radar de telle manière qu'il ne considère que le signal d'écho dû à la cible mobile mais pas les encombrements.
Pour cela, Radar utilise le principe de l'effet Doppler pour distinguer les cibles non stationnaires des objets stationnaires. Ce type de radar est appelé Radar indicateur de cible mobile ou simplement,MTI Radar.
Selon Doppler effect, la fréquence du signal reçu augmentera si la cible se déplace vers la direction du radar. De même, la fréquence du signal reçu diminuera si la cible s'éloigne du radar.
Types de radars MTI
Nous pouvons classer les radars MTI comme suit two types en fonction du type d'émetteur utilisé.
- Radar MTI avec émetteur d'amplificateur de puissance
- Radar MTI avec émetteur d'oscillateur de puissance
Maintenant, parlons de ces deux radars MTI un par un.
Radar MTI avec émetteur d'amplificateur de puissance
Le radar MTI utilise une seule antenne pour la transmission et la réception de signaux à l'aide du duplexeur. leblock diagram du radar MTI avec émetteur amplificateur de puissance est illustré dans la figure suivante.

le function de chaque bloc de radar MTI avec émetteur amplificateur de puissance est mentionné ci-dessous.
Pulse Modulator - Il produit un signal modulé par impulsions et il est appliqué à l'amplificateur de puissance.
Power Amplifier - Il amplifie les niveaux de puissance du signal modulé par impulsions.
Local Oscillator - Il produit un signal ayant une fréquence stable $f_l$. Par conséquent, il est également appelé oscillateur local stable. La sortie de l'Oscillateur Local est appliquée à la fois au Mixer-I et au Mixer-II.
Coherent Oscillator - Il produit un signal ayant une fréquence intermédiaire, $f_c$. Ce signal est utilisé comme signal de référence. La sortie de Coherent Oscillator est appliquée à la fois au Mixer-I et au Phase Detector.
Mixer-I- Le mélangeur peut produire la somme ou la différence des fréquences qui lui sont appliquées. Les signaux ayant des fréquences de$f_l$ et $f_c$sont appliqués à Mixer-I. Ici, le Mixer-I est utilisé pour produire la sortie, qui a la fréquence$f_l+f_c$.
Duplexer- Il s'agit d'un commutateur à micro-ondes, qui relie l'antenne à la section émetteur ou à la section récepteur en fonction des besoins. L'antenne transmet le signal ayant la fréquence$f_l+f_c$lorsque le duplexeur connecte l'antenne à l'amplificateur de puissance. De même, l'antenne reçoit le signal ayant une fréquence de$f_l+f_c\pm f_d$ lorsque le duplexeur connecte l'antenne à Mixer-II.
Mixer-II- Le mélangeur peut produire la somme ou la différence des fréquences qui lui sont appliquées. Les signaux ayant des fréquences$f_l+f_c\pm f_d$ et $f_l$sont appliqués à Mixer-II. Ici, le Mixer-II est utilisé pour produire la sortie, qui a la fréquence$f_c\pm f_d$.
IF Amplifier- L'amplificateur IF amplifie le signal de fréquence intermédiaire (IF). L'amplificateur IF illustré sur la figure amplifie le signal ayant une fréquence$f_c+f_d$. Ce signal amplifié est appliqué en tant qu'entrée au détecteur de phase.
Phase Detector - Il est utilisé pour produire le signal de sortie ayant une fréquence $f_d$ à partir des deux signaux d'entrée appliqués, qui ont les fréquences de $f_c+f_d$ et $f_c$. La sortie du détecteur de phase peut être connectée à l'annuleur de ligne de retard.
Radar MTI avec émetteur d'oscillateur de puissance
Le schéma de principe du radar MTI avec émetteur d'oscillateur de puissance ressemble au schéma de principe du radar MTI avec émetteur d'amplificateur de puissance. Les blocs correspondant à la section du récepteur seront les mêmes dans les deux schémas de principe. Tandis que les blocs correspondant à la section d'émetteur peuvent différer dans les deux schémas de principe.
le block diagram du radar MTI avec émetteur d'oscillateur de puissance est illustré dans la figure suivante.

Comme le montre la figure, le radar MTI utilise l'antenne unique pour la transmission et la réception de signaux à l'aide du duplexeur. leoperation du radar MTI avec émetteur d'oscillateur de puissance est mentionné ci-dessous.
La sortie de l'oscillateur magnétron et la sortie de l'oscillateur local sont appliquées à Mixer-I. Cela produira en outre unIF signaldont la phase est directement liée à la phase du signal émis.
La sortie de Mixer-I est appliquée à l'oscillateur cohérent. Par conséquent, la phase de sortie de l'oscillateur cohérent seralockedà la phase du signal IF. Cela signifie que la phase de la sortie de l'oscillateur cohérent sera également directement liée à la phase du signal transmis.
Ainsi, la sortie de l'oscillateur cohérent peut être utilisée comme signal de référence pour comparer le signal d'écho reçu avec le signal transmis correspondant en utilisant phase detector.
Les tâches ci-dessus seront répétées pour chaque signal nouvellement transmis.
Systèmes radar - Annuleurs de ligne à retard
Dans ce chapitre, nous découvrirons les annuleurs de ligne à retard dans les systèmes radar. Comme son nom l'indique, la ligne à retard introduit un certain délai. Ainsi, la ligne à retard est principalement utilisée dans l'annuleur de ligne à retard afin d'introduire undelay du temps de répétition des impulsions.
Delay line cancellerest un filtre, qui élimine les composantes CC des signaux d'écho reçus de cibles fixes. Cela signifie qu'il autorise les composantes CA des signaux d'écho reçus de cibles non stationnaires, c'est-à-dire de cibles mobiles.
Types d'annuleurs de ligne à retard
Les annuleurs de ligne à retard peuvent être classés comme suit two types en fonction du nombre de lignes à retard qui y sont présentes.
- Annuleur de ligne à retard unique
- Annuleur de ligne à double retard
Dans nos sections suivantes, nous discuterons plus en détail de ces deux annuleurs de ligne de retard.
Annuleur de ligne à retard unique
La combinaison d'une ligne à retard et d'un soustracteur est connue sous le nom d'annuleur de ligne à retard. Il est également appelé annuleur de ligne à délai unique. leblock diagram du récepteur MTI avec annuleur de ligne à retard unique est illustré dans la figure ci-dessous.
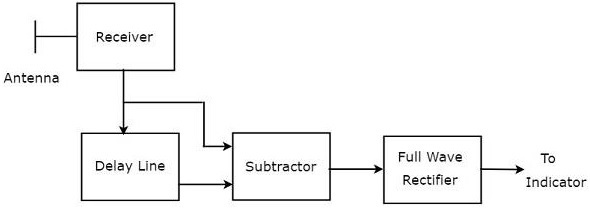
Nous pouvons écrire le mathematical equation du signal d'écho reçu après l'effet Doppler comme -
$$V_1=A\sin\left [ 2\pi f_dt-\phi_0 \right ]\:\:\:\:\:Equation\:1$$
Où,
A est l'amplitude du signal vidéo
$f_d$ est la fréquence Doppler
$\phi_o$ est le déphasage et il est égal à $4\pi f_tR_o/C$
Nous obtiendrons le output of Delay line canceller, en remplaçant $t$ par $t-T_P$ dans l'équation 1.
$$V_2=A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]\:\:\:\:\:Equation\:2$$
Où,
$T_P$ est le temps de répétition des impulsions
Nous obtiendrons le subtractor output en soustrayant l'équation 2 de l'équation 1.
$$V_1-V_2=A\sin\left [ 2\pi f_dt-\phi_0 \right ]-A\sin\left [ 2\pi f_d\left ( t-T_P\right )-\phi_0 \right ]$$
$$\Rightarrow V_1-V_2=2A\sin\left [ \frac{ 2\pi f_dt-\phi_0-\left [ 2\pi f_d\left ( t-T_P \right )-\phi_0 \right ]}{2}\right ]\cos\left [ \frac{ 2\pi f_dt-\phi_o+2\pi f_d\left ( t-T_P \right )-\phi_0 }{2}\right ]$$
$$V_1-V_2=2A\sin\left [ \frac{2\pi f_dT_P}{2} \right ]\cos\left [ \frac{2\pi f_d\left ( 2t-T_P \right )-2\phi_0}{2} \right ]$$
$$\Rightarrow V_1-V_2=2A\sin\left [ \pi f_dT_p \right ]\cos\left [ 2\pi f_d\left ( t-\frac{T_P}{2} \right )-\phi_0 \right ]\:\:\:\:\:Equation\:3$$
La sortie du soustracteur est appliquée comme entrée au redresseur Full Wave. Par conséquent, la sortie de Full Wave Rectifier ressemble à celle illustrée dans la figure suivante. Ce n'est rien d'autre que lefrequency response de l'annuleur de ligne à retard unique.

À partir de l'équation 3, nous pouvons observer que la réponse en fréquence de l'annuleur de ligne à retard unique devient nulle, lorsque $\pi f_dT_P$ est égal à integer multiples of $\pi$ Ça signifie, $\pi f_dT_P$ est égal à $n\pi$ Mathématiquement, il peut être écrit comme
$$\pi f_dT_P=n\pi$$
$$\Rightarrow f_dT_P=n$$
$$\Rightarrow f_d=\frac{n}{T_P}\:\:\:\:\:Equation\:4$$
À partir de l'équation 4, nous pouvons conclure que la réponse en fréquence de l'annuleur de ligne à retard unique devient nulle, lorsque la fréquence Doppler $f_d$ est égal à des multiples entiers de l'inverse du temps de répétition des impulsions $T_P$.
Nous connaissons la relation suivante entre le temps de répétition des impulsions et la fréquence de répétition des impulsions.
$$f_d=\frac{1}{T_P}$$
$$\Rightarrow \frac{1}{T_P}=f_P\:\:\:\:\:Equation\:5$$
Nous obtiendrons l'équation suivante, en remplaçant l'équation 5 dans l'équation 4.
$$\Rightarrow f_d=nf_P\:\:\:\:\:Equation\:6$$
À partir de l'équation 6, nous pouvons conclure que la réponse en fréquence de l'annuleur de ligne à retard unique devient nulle, lorsque la fréquence Doppler, $f_d$ est égal à des multiples entiers de la fréquence de répétition des impulsions $f_P$.
Vitesses aveugles
D'après ce que nous avons appris jusqu'à présent, l'annuleur de ligne à retard unique élimine les composantes CC des signaux d'écho reçus de cibles stationnaires, lorsque $n$est égal à zéro. En plus de cela, il élimine également les composantes AC des signaux d'écho reçus de cibles non stationnaires, lorsque la fréquence Doppler$f_d$ est égal à un entier (other than zero) multiples de la fréquence de répétition des impulsions $f_P$.
Ainsi, les vitesses relatives pour lesquelles la réponse en fréquence de l'annuleur de ligne à retard unique devient nulle sont appelées blind speeds. Mathématiquement, nous pouvons écrire l'expression pour la vitesse aveugle$v_n$ comme -
$$v_n=\frac{n\lambda}{2T_P}\:\:\:\:\:Equation\:7$$
$$\Rightarrow v_n=\frac{n\lambda f_P}{2}\:\:\:\:\:Equation\:8$$
Où,
$n$ est un entier égal à 1, 2, 3 et ainsi de suite
$\lambda$ est la longueur d'onde de fonctionnement
Exemple de problème
Un radar MTI fonctionne à une fréquence de $6GHZ$ avec une fréquence de répétition des impulsions de $1KHZ$. Trouvez le premier, le deuxième et le troisièmeblind speeds de ce radar.
Solution
Donné,
La fréquence de fonctionnement du radar MTI, $f=6GHZ$
Fréquence de répétition des impulsions, $f_P=1KHZ$.
Voici la formule pour operating wavelength $\lambda$ en termes de fréquence de fonctionnement, f.
$$\lambda=\frac{C}{f}$$
Remplacer, $C=3\times10^8m/sec$ et $f=6GHZ$ dans l'équation ci-dessus.
$$\lambda=\frac{3\times10^8}{6\times10^9}$$
$$\Rightarrow \lambda=0.05m$$
Alors le operating wavelength $\lambda$ est égal à $0.05m$, lorsque la fréquence de fonctionnement f est $6GHZ$.
Nous savons ce qui suit formula for blind speed.
$$v_n=\frac{n\lambda f_p}{2}$$
En remplaçant, $n$= 1,2 & 3 dans l'équation ci-dessus, nous obtiendrons les équations suivantes pour les première, deuxième et troisième vitesses aveugles respectivement.
$$v_1=\frac{1\times \lambda f_p}{2}=\frac{\lambda f_p}{2}$$
$$v_2=\frac{2\times \lambda f_p}{2}=2\left ( \frac{\lambda f_p}{2} \right )=2v_1$$
$$v_3=\frac{3\times \lambda f_p}{2}=3\left ( \frac{\lambda f_p}{2} \right )=3v_1$$
Substitute les valeurs de $\lambda$ et $f_P$ dans l'équation de la première vitesse aveugle.
$$v_1=\frac{0.05\times 10^3}{2}$$
$$\Rightarrow v_1=25m/sec$$
Par conséquent, la first blind speed $v_1$ est égal à $25m/sec$ pour les spécifications données.
Nous obtiendrons les valeurs de second & third blind speeds comme $50m/sec$& $75m/sec$ respectivement en substituant la valeur de ð ?? '£ 1 dans les équations des deuxième et troisième vitesses aveugles.
Annuleur de ligne à double retard
Nous savons qu'un annuleur de ligne à retard unique se compose d'une ligne à retard et d'un soustracteur. Si deux annuleurs de ligne à retard de ce type sont mis en cascade ensemble, alors cette combinaison est appelée annuleur de ligne à retard double. leblock diagram de l'annuleur de ligne à double retard est illustré dans la figure suivante.

Laisser $p\left ( t \right )$ et $q\left ( t \right )$être l'entrée et la sortie du premier annuleur de ligne à retard. Nous obtiendrons la relation mathématique suivante à partir defirst delay line canceller.
$$q\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )\:\:\:\:\:Equation\:9$$
La sortie du premier annuleur de ligne à retard est appliquée en tant qu'entrée au second annuleur de ligne à retard. Par conséquent,$q\left ( t \right )$sera l'entrée du deuxième annuleur de ligne à retard. Laisser$r\left ( t \right )$être la sortie du deuxième annuleur de ligne à retard. Nous obtiendrons la relation mathématique suivante à partir dusecond delay line canceller.
$$r\left ( t \right )=q\left ( t \right )-q\left ( t-T_P \right )\:\:\:\:\:Equation\:10$$
Remplacer $t$ par $t-T_P$ dans l'équation 9.
$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-T_P-T_P \right )$$
$$q\left ( t-T_P \right )=p\left ( t-T_P \right )-p\left ( t-2T_P \right )\:\:\:\:\:Equation\:11$$
Substitute, Équation 9 et équation 11 de l'équation 10.
$$r\left ( t \right )=p\left ( t \right )-p\left ( t-T_P \right )-\left [ p\left ( t-T_P \right )-p\left ( t-2T_P \right ) \right ]$$
$$\Rightarrow r\left ( t \right )=p\left ( t \right )-2p\left ( t-T_P \right )+p\left ( t-2T_P \right )\:\:\:\:\:Equation\:12$$
le advantagede l'annuleur de ligne à retard double est qu'il rejette largement le fouillis. La sortie de deux annuleurs de ligne à retard, qui sont en cascade, sera égale au carré de la sortie de l'annuleur de ligne à retard unique.
Ainsi, l'amplitude de la sortie du double annuleur de ligne à retard, qui est présent au récepteur radar MTI sera égale à $4A^2\left ( \sin\left [ \pi f_dT_P \right ] \right )^2$.

Les caractéristiques de réponse en fréquence de l'annuleur de ligne à retard double et de la combinaison en cascade de deux annuleurs de ligne à retard sont les mêmes. leadvantage de l'annuleur de ligne à retard dans le domaine temporel est qu'il peut être utilisé pour toutes les plages de fréquences.
Systèmes radar - Radar de poursuite
Le radar, qui est utilisé pour suivre la trajectoire d'une ou de plusieurs cibles, est appelé Tracking Radar. En général, il exécute les fonctions suivantes avant de démarrer l'activité de suivi.
- Détection de cible
- Portée de la cible
- Recherche d'angles d'élévation et d'azimut
- Recherche du décalage de fréquence Doppler
Ainsi, le radar de suivi suit la cible en suivant l'un des trois paramètres - plage, angle, décalage de fréquence Doppler. La plupart des radars de suivi utilisent leprinciple of tracking in angle. Voyons maintenant ce qu'est le suivi angulaire.
Suivi angulaire
Les faisceaux de crayon de l'antenne radar effectuent un suivi en angle. L'axe de l'antenne radar est considéré comme la direction de référence. Si la direction de la cible et la direction de référence ne sont pas les mêmes, il y auraangular error, qui n'est rien d'autre que la différence entre les deux directions.
Si le signal d'erreur angulaire est appliqué à un système de servocommande, alors il déplacera l'axe de l'antenne radar vers la direction de la cible. L'axe de l'antenne radar et la direction de la ciblecoincidelorsque l'erreur angulaire est nulle. Il existe un mécanisme de rétroaction dans le radar de suivi, qui fonctionne jusqu'à ce que l'erreur angulaire devienne nulle.
Voici les two techniques, qui sont utilisés dans le suivi angulaire.
- Lobage séquentiel
- Balayage conique
Maintenant, laissez-nous discuter de ces deux techniques une par une.
Lobage séquentiel
Si les faisceaux d'antenne sont commutés entre deux modèles alternativement pour suivre la cible, alors il est appelé sequential lobing. Il est également appelé commutation séquentielle et commutation de lobe. Cette technique est utilisée pour trouver l'erreur angulaire dans une coordonnée. Il donne les détails de l'amplitude et de la direction de l'erreur angulaire.
La figure suivante montre un exemple de lobage séquentiel dans polar coordinates.
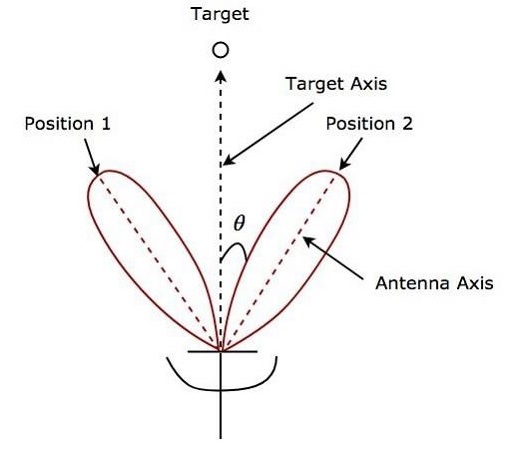
Comme le montre la figure, les faisceaux d'antenne basculent alternativement entre la position 1 et la position 2. L'erreur angulaire θ est indiquée sur la figure ci-dessus. Le lobage séquentiel donne la position de la cible avec une grande précision. C'est le principaladvantage de lobage séquentiel.
Balayage conique
Si le faisceau de l'antenne tourne en continu pour suivre une cible, il est appelé conical scanning. La modulation de balayage conique est utilisée pour trouver la position de la cible. La figure suivante montre un exemple de balayage conique.

Squint angleest l'angle entre l'axe du faisceau et l'axe de rotation et il est montré dans la figure ci-dessus. Le signal d'écho obtenu de la cible est modulé à une fréquence égale à la fréquence à laquelle le faisceau d'antenne tourne.
L'angle entre la direction de la cible et l'axe de rotation détermine le amplitude of the modulated signal. Ainsi, la modulation de balayage conique doit être extraite du signal d'écho, puis elle doit être appliquée au système de commande d'asservissement, qui déplace l'axe du faisceau de l'antenne vers la direction de la cible.
Systèmes radar - Paramètres d'antenne
Un Antenna ou Aerial est un transducteur, qui convertit l'énergie électrique en ondes électromagnétiques et vice versa.
Une antenne a les paramètres suivants -
- Directivity
- Efficacité d'ouverture
- Efficacité de l'antenne
- Gain
Maintenant, laissez-nous discuter de ces paramètres en détail -
Directivité
Selon la définition standard, «Le rapport de l'intensité de rayonnement maximale de l'antenne en question à l'intensité de rayonnement d'une antenne isotrope ou de référence, rayonnant la même puissance totale est appelé le Directivity. »
Bien qu'une antenne rayonne de puissance, la direction dans laquelle elle rayonne est d'une grande importance. L'antenne à l'étude est appeléesubject Antenna. Son intensité de rayonnement est focalisée dans une direction particulière, pendant qu'il émet ou reçoit. Par conséquent, on dit que l'antenne a sa directivité dans cette direction particulière.
Le rapport de l'intensité de rayonnement dans une direction donnée d'une antenne à l'intensité de rayonnement moyennée dans toutes les directions, est appelé Directivity.
Si cette direction particulière n'est pas spécifiée, alors la direction dans laquelle l'intensité maximale est observée peut être considérée comme la directivité de cette antenne.
La directivité d'une antenne non isotrope est égale au rapport de l'intensité de rayonnement dans une direction donnée à l'intensité de rayonnement de la source isotrope.
Mathematically, nous pouvons écrire l'expression pour la directivité comme -
$$Directivity=\frac{U_{Max}\left (\theta,\phi\right )}{U_0}$$
Où,
$U_{Max}\left (\theta,\phi\right )$ est l'intensité de rayonnement maximale de l'antenne du sujet
$U_0$ est l'intensité de rayonnement d'une antenne isotrope.
Efficacité d'ouverture
Selon la définition standard, “Aperture efficiency d'une antenne est le rapport de la zone de rayonnement effective (ou de la zone effective) à la zone physique de l'ouverture. "
Une antenne émet de la puissance à travers une ouverture. Ce rayonnement doit être efficace avec un minimum de pertes. La zone physique de l'ouverture doit également être prise en considération, car l'efficacité du rayonnement dépend de la zone de l'ouverture, physiquement sur l'antenne.
Mathematically, nous pouvons écrire l'expression de l'efficacité d'Aperture $\epsilon_A$ comme
$$\epsilon _A=\frac{A_{eff}}{A_p}$$
Où,
$A_{eff}$ est la zone efficace
$A_P$ est la zone physique
Efficacité de l'antenne
Selon la définition standard, “Antenna Efficiency est le rapport entre la puissance rayonnée de l’antenne et la puissance d’entrée acceptée par l’antenne. »
Toute antenne est conçue pour émettre de la puissance avec un minimum de pertes, pour une entrée donnée. L'efficacité d'une antenne explique à quel point une antenne est capable de fournir sa sortie efficacement avec des pertes minimales dans la ligne de transmission. Il est également appeléRadiation Efficiency Factor de l'antenne.
Mathematically, nous pouvons écrire l'expression pour l'efficacité de l'antenne 𝜂𝑒 comme -
$$\eta _e=\frac{P_{Rad}}{P_{in}}$$
Où,
$P_{Rad}$ est la quantité de puissance rayonnée
$P_{in}$ est la puissance d'entrée de l'antenne
Gain
Selon la définition standard, “Gain d'une antenne est le rapport de l'intensité de rayonnement dans une direction donnée à l'intensité de rayonnement qui serait obtenue si la puissance acceptée par l'antenne était rayonnée de manière isotrope.
Simplement, Gaind'une antenne prend en compte la directivité de l'antenne ainsi que ses performances effectives. Si la puissance acceptée par l'antenne était rayonnée de manière isotrope (c'est-à-dire dans toutes les directions), alors l'intensité de rayonnement que nous obtenons peut être considérée comme un référentiel.
Le terme Antenna gain décrit la quantité d'énergie transmise dans la direction du rayonnement de pointe vers celle d'une source isotrope.
Le gain est généralement mesuré en dB.
Contrairement à la directivité, le gain d'antenne prend également en compte les pertes qui se produisent et se concentre donc sur l'efficacité.
Mathematically, nous pouvons écrire l'expression pour Antenna Gain $G$ comme -
$$G=\eta_eD$$
Où,
$\eta_e$ est l'efficacité de l'antenne
$D$ est la directivité de l'antenne
Systèmes radar - Antennes radar
Dans ce chapitre, découvrons les antennes, qui sont utiles dans la communication radar. Nous pouvons classer les antennes radar comme suittwo types basé sur la structure physique.
- Antennes à réflecteur parabolique
- Antennes d'objectif
Dans nos sections suivantes, nous discuterons en détail des deux types d'antennes.
Antennes à réflecteur parabolique
Les antennes à réflecteur parabolique sont les antennes micro-ondes. Une connaissance du réflecteur parabolique est essentielle pour comprendre le fonctionnement des antennes en profondeur.
Principe d'opération
Parabola n'est rien d'autre que le Locus des points, qui se déplacent de telle sorte que sa distance du point fixe (appelé focus) plus sa distance d'une ligne droite (appelée Directrice) soit constante.
La figure suivante montre le geometry of parabolic reflector. Les points F et V sont respectivement le foyer (l'alimentation est donnée) et le sommet. La droite joignant F et V est l'axe de symétrie.$P_1Q_1, P_2Q_2$ et $P_3Q_3$sont les rayons réfléchis. La ligne L représente la directrice sur laquelle reposent les points réfléchis (pour dire qu'ils sont colinéaires).

Comme le montre la figure, la distance entre F et L est constante par rapport aux ondes focalisées. L'onde réfléchie forme un front d'onde collimaté, hors de la forme parabolique. Le rapport de la distance focale à la taille d'ouverture (c.-à-d.$f/D$ ) est connu comme “f over D ratio”. C'est un paramètre important du réflecteur parabolique et sa valeur varie de0.25 to 0.50.
le law of reflectiondéclare que l'angle d'incidence et l'angle de réflexion sont égaux. Cette loi lorsqu'elle est utilisée avec une parabole aide à la focalisation du faisceau. La forme de la parabole lorsqu'elle est utilisée à des fins de réflexion des ondes, présente certaines propriétés de la parabole, qui sont utiles pour construire une antenne, en utilisant les ondes réfléchies.
Propriétés de Parabola
Voici les différentes propriétés de Parabola -
Toutes les ondes issues de la mise au point se reflètent sur l'axe parabolique. Par conséquent, toutes les ondes atteignant l'ouverture sont en phase.
Comme les ondes sont en phase, le faisceau de rayonnement le long de l'axe parabolique sera fort et concentré.
En suivant ces points, les réflecteurs paraboliques aident à produire une directivité élevée avec une largeur de faisceau plus étroite.
Construction et fonctionnement d'un réflecteur parabolique
Si une antenne à réflecteur parabolique est utilisée pour transmitting a signal, le signal de l'alimentation sort d'une antenne dipôle ou d'une antenne cornet, pour focaliser l'onde sur la parabole. Cela signifie que les ondes sortent du point focal et frappent le réflecteur paraboloïde. Cette onde est maintenant réfléchie sous forme de front d'onde collimaté, comme indiqué précédemment, pour être transmise.
La même antenne est utilisée comme receiver. Lorsque l'onde électromagnétique atteint la forme de la parabole, l'onde est réfléchie sur le point d'alimentation. L'antenne dipôle ou l'antenne cornet, qui agit en tant qu'antenne réceptrice à son alimentation, reçoit ce signal, pour le convertir en signal électrique et le transmettre au circuit récepteur.
Le gain du paraboloïde est fonction du rapport d'ouverture $D/\lambda$. La puissance rayonnée effective(ERP) d'une antenne est la multiplication de la puissance d'entrée fournie à l'antenne et son gain de puissance.
Habituellement, une antenne à cornet de guidage d'ondes est utilisée comme radiateur d'alimentation pour l'antenne à réflecteur paraboloïde. Parallèlement à cette technique, nous avons les deux types d'alimentation suivants donnés à l'antenne à réflecteur paraboloïde.
- Alimentation Cassegrain
- Grégorien
Alimentation Cassegrain
Dans ce type, l'alimentation est située au sommet du paraboloïde, contrairement au réflecteur parabolique. Un réflecteur de forme convexe, qui agit comme un hyperboloïde, est placé à l'opposé de l'alimentation de l'antenne. Il est également connu sous le nom desecondary hyperboloid reflectorou sous-réflecteur. Il est placé de telle manière que l'un de ses foyers coïncide avec le foyer du paraboloïde. Ainsi, l'onde est réfléchie deux fois.
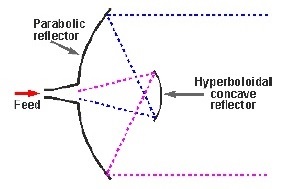
La figure ci-dessus montre le modèle de travail de l'alimentation de cassegrain.
Grégorien
Le type d'alimentation où il existe une paire de certaines configurations et où la largeur du faisceau d'alimentation est progressivement augmentée tandis que les dimensions de l'antenne sont maintenues fixes est appelé Gregorian feed. Ici, l'hyperboloïde de forme convexe de Cassegrain est remplacé par un réflecteur paraboloïde de forme concave, qui est bien sûr de plus petite taille.
Ces réflecteurs de type grégorien peuvent être utilisés des quatre manières suivantes -
Systèmes grégoriens utilisant un réflecteur secondaire ellipsoïdal aux foyers F1.
Systèmes grégoriens utilisant un réflecteur secondaire ellipsoïdal aux foyers F2.
Systèmes Cassegrain utilisant un sous-réflecteur hyperboloïde (convexe).
Systèmes Cassegrain utilisant un sous-réflecteur hyperboloïde (concave mais l'alimentation étant très proche).
Parmi les différents types d'antennes à réflecteur, les réflecteurs paraboliques simples et les réflecteurs paraboliques à alimentation Cassegrain sont les plus couramment utilisés.
Antennes d'objectif
Les antennes d'objectif utilisent la surface incurvée pour la transmission et la réception des signaux. Ces antennes sont constituées de verre, où les propriétés convergentes et divergentes de la lentille sont suivies. lefrequency range de l'utilisation de l'antenne d'objectif commence à 1 GHz mais son utilisation est plus grande à 3 GHz and above.
Une connaissance de la lentille est nécessaire pour comprendre en profondeur le fonctionnement de l'antenne de la lentille. Rappelez-vous qu'une lentille en verre normale fonctionne sur leprinciple of refraction.
Construction et fonctionnement de l'antenne d'objectif
Si une source lumineuse est supposée être présente à un point focal d'une lentille, qui est à une distance focale de la lentille, alors les rayons traversent la lentille comme collimatés ou parallel rays sur le front d'onde plan.
Il y a deux phénomènes qui se produisent lorsque les rayons tombent de différents côtés d'une lentille. Ils sont donnés ici -
Les rayons qui traversent le centre de la lentille sont moins réfractés que les rayons qui traversent les bords de la lentille. Tous les rayons sont envoyés parallèlement au front d'onde plan. Ce phénomène de Lens est appelé commeDivergence.
La même procédure est inversée si un faisceau lumineux est envoyé du côté droit vers le côté gauche du même objectif. Ensuite, le faisceau est réfracté et se rencontre en un point appelé le point focal, à une distance focale de l'objectif. Ce phénomène s'appelleConvergence.
Le schéma suivant nous aidera à mieux comprendre le phénomène.
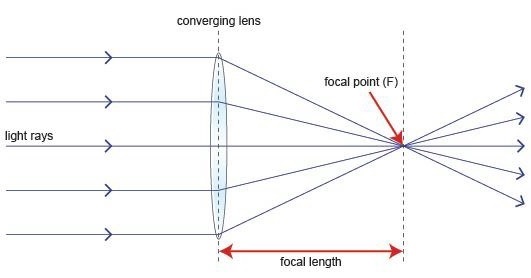
le ray diagramreprésente le point focal et la distance focale de la source à l'objectif. Les rayons parallèles obtenus sont également appelés rayons collimatés.
Sur la figure ci-dessus, la source au point focal, à une distance focale de l'objectif est collimatée dans le front d'onde plan. Ce phénomène peut être inversé, ce qui signifie que la lumière, si elle est envoyée du côté gauche, converge vers le côté droit de la lentille.
C'est à cause de ça reciprocity, la lentille peut être utilisée comme antenne, car le même phénomène aide à utiliser la même antenne pour la transmission et la réception.
Pour obtenir les propriétés de focalisation à des fréquences plus élevées, l'indice de réfraction doit être inférieur à l'unité. Quel que soit l'indice de réfraction, l'objectif de Lens est de redresser la forme d'onde. Sur cette base, le plan E et la lentille du plan H sont développés, qui retardent ou accélèrent également le front d'onde.
Systèmes radar - Récepteur de filtre assorti
Si un filtre produit une sortie de telle manière qu'il maximise le rapport entre la puissance de crête de sortie et la puissance de bruit moyenne dans sa réponse en fréquence, alors ce filtre est appelé Matched filter.
C'est un critère important, qui est pris en compte lors de la conception de tout récepteur radar. Dans ce chapitre, discutons de la fonction de réponse en fréquence du filtre adapté et de la réponse impulsionnelle du filtre adapté.
Fonction de réponse en fréquence du filtre adapté
La réponse en fréquence du filtre adapté sera proportionnelle au conjugué complexe du spectre du signal d'entrée. Mathématiquement, nous pouvons écrire l'expression pourfrequency response function, $H\left (f\right )$ du filtre correspondant comme -
$$H\left (f\right )=G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:Equation\:1$$
Où,
$G_a$ est le gain maximum du filtre correspondant
$S\left (f\right )$ est la transformée de Fourier du signal d'entrée, $s\left (t\right )$
$S^\ast\left (f\right )$ est le conjugué complexe de $S\left (f\right )$
$t_1$ est l'instant auquel le signal observé est maximum
En général, la valeur de $G_a$est considéré comme un. Nous obtiendrons l'équation suivante en remplaçant$G_a=1$ dans l'équation 1.
$$H\left (f\right )=S^\ast\left (f\right )e^{-j2\pi ft_1}\:\:\:\:\:Equation\:2$$
La fonction de réponse en fréquence, $H\left (f\right )$ du filtre correspondant a le magnitude de $S^\ast\left (f\right )$ et phase angle de $e^{-j2\pi ft_1}$, qui varie uniformément avec la fréquence.
Réponse impulsionnelle du filtre correspondant
Dans time domain, nous obtiendrons la sortie, $h(t)$ du récepteur de filtre adapté en appliquant la transformée de Fourier inverse de la fonction de réponse en fréquence, $H(f)$.
$$h\left (t\right )=\int_{-\infty }^{\infty }H\left (f\right )e^{-j2\pi ft_1}df\:\:\:\:\:Equation\:3$$
Substitute, Équation 1 de l'équation 3.
$$h\left (t\right )=\int_{-\infty }^{\infty }\lbrace G_aS^\ast\left (f\right )e^{-j2\pi ft_1}\rbrace e^{j2\pi ft}df$$
$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\ast\left (f\right )e^{-j2\pi f\left (t_1-t\right )}df\:\:\:\:\:Equation\:4$$
Nous connaissons la relation suivante.
$$S^\ast\left (f\right )=S\left (-f\right )\:\:\:\:\:Equation\:5$$
Substitute, Équation 5 de l'équation 4.
$$h\left (t\right )=\int_{-\infty }^{\infty }G_aS(-f)e^{-j2\pi f\left (t_1-t\right )}df$$
$$\Rightarrow h\left (t\right )=\int_{-\infty }^{\infty }G_aS^\left (f\right )e^{j2\pi f\left (t_1-t\right )}df$$
$$\Rightarrow h\left (t\right )=G_as(t_1−t)\:\:\:\:\:Equation\:6$$
En général, la valeur de $G_a$est considéré comme un. Nous obtiendrons l'équation suivante en remplaçant$G_a=1$ dans l'équation 6.
$$h(t)=s\left (t_1-t\right )$$
L'équation ci-dessus prouve que le impulse response of Matched filter est l'image miroir du signal reçu à environ un instant de temps $t_1$. Les figures suivantes illustrent ce concept.


Le signal reçu, $s\left (t\right )$ et la réponse impulsionnelle, $h\left (t\right )$ du filtre adapté correspondant au signal, $s\left (t\right )$ sont illustrés dans les figures ci-dessus.
Systèmes radar - Affichages radar
Un instrument électronique, qui est utilisé pour afficher les données visuellement, est appelé affichage. Ainsi, l'instrument électronique qui affiche visuellement les informations sur la cible du radar est appeléRadar display. Il montre visuellement les informations du signal d'écho sur l'écran.
Types d'affichages radar
Dans cette section, nous découvrirons les différents types d'affichages radar. Les affichages radar peuvent être classés dans les types suivants.
A-Scope
C'est un affichage radar bidimensionnel. Les coordonnées horizontales et verticales représentent respectivement la portée et l'amplitude de l'écho de la cible. Dans A-Scope, la modulation de déviation a lieu. Il est plus approprié pourmanually tracking Radar.
B-Scope
C'est un affichage radar bidimensionnel. Les coordonnées horizontales et verticales représentent respectivement l'angle azimutal et la portée de la cible. Dans B-Scope, la modulation d'intensité a lieu. Il est plus approprié pourmilitary Radars.
C-Scope
Il s'agit d'un affichage radar bidimensionnel. Les coordonnées horizontales et verticales représentent respectivement l'angle azimutal et l'angle d'élévation. Dans C-Scope, la modulation d'intensité a lieu.
D-Scope
Si le faisceau d'électrons est dévié ou si le point modulé en intensité apparaît sur l'écran radar en raison de la présence de la cible, on parle alors de blip. C-Scope devient D-Scope, lorsque les blips s'étendent verticalement afin de fournir la distance.
E-Scope
Il s'agit d'un affichage radar bidimensionnel. Les coordonnées horizontales et verticales représentent respectivement la distance et l'angle d'élévation. Dans E-Scope, la modulation d'intensité a lieu.
Portée F
Si l'antenne radar est dirigée vers la cible, alors F-Scope affiche la cible sous la forme d'un blip centralisé. Ainsi, les déplacements horizontaux et verticaux du blip représentent respectivement les erreurs de visée horizontale et verticale.
G-Scope
Si l'antenne radar est dirigée vers la cible, alors G-Scope affiche la cible sous forme de blip centralisé latéralement. Les déplacements horizontaux et verticaux du blip représentent respectivement les erreurs de visée horizontale et verticale.
Portée H
Il s'agit de la version modifiée de B-Scope afin de fournir des informations sur l'angle d'élévation de la cible. Il affiche la cible sous forme de deux spots, qui sont étroitement espacés. Cela peut être approximé à une courte ligne brillante et la pente de cette ligne sera proportionnelle au sinus de l'angle d'élévation.
I-Scope
Si l'antenne radar est dirigée vers la cible, l'I-Scope affiche la cible sous la forme d'un circle. Le rayon de ce cercle sera proportionnel à la distance de la cible. Si l'antenne radar ne vise pas correctement la cible, l'I-Scope affiche la cible sous forme de segment au lieu de cercle. La longueur de l'arc de ce segment sera inversement proportionnelle à l'amplitude de l'erreur de pointage.
J-Scope
C'est la version modifiée d'A-Scope. Il affiche la cible sous forme de déviation radiale par rapport à la base de temps.
K-Scope
C'est la version modifiée d'A-Scope. Si l'antenne radar est dirigée vers la cible, alors K-Scope affiche la cible comme une paire de déviations verticales, qui ont la même hauteur. Si l'antenne radar ne vise pas correctement la cible, il y aura une erreur de pointage. Ainsi, la magnitude et la direction de l'erreur de pointage dépendent de la différence entre les deux déflexions verticales.
L-Scope
Si l'antenne radar est dirigée vers la cible, alors L-Scope affiche la cible sous forme de deux spots horizontaux d'amplitude égale. Un blip horizontal se trouve à droite de la base de temps verticale centrale et l'autre se trouve à gauche de la base de temps verticale centrale.
M-Scope
C'est la version modifiée d'A-Scope. Un signal de piédestal réglable doit être déplacé le long de la ligne de base jusqu'à ce qu'il coïncide avec les déviations du signal, qui proviennent de la position horizontale de la cible. De cette manière, la distance de la cible peut être déterminée.
N-Scope
C'est la version modifiée de K-Scope. Un signal de piédestal réglable est utilisé pour mesurer la distance.
O-Scope
C'est la version modifiée d'A-Scope. Nous obtiendrons O-Scope, en incluant une encoche ajustable à A-Scope pour mesurer la distance.
P-Scope
C'est un affichage radar, qui utilise la modulation d'intensité. Il affiche les informations du signal d'écho sous forme de vue en plan. La distance et l'angle azimutal sont affichés en coordonnées polaires. Par conséquent, il est appelé lePlan Position Indicator ou la PPI display.
R-Scope
C'est un affichage radar, qui utilise la modulation d'intensité. Les coordonnées horizontales et verticales représentent respectivement la portée et la hauteur de la cible. Par conséquent, il est appeléRange-Height Indicator ou RHI display.
Systèmes radar - Duplexeurs
En communication bidirectionnelle, si nous sommes censés utiliser la même antenne pour la transmission et la réception des signaux, nous avons besoin d'un duplexeur. Duplexerest un commutateur à micro-ondes, qui relie l'antenne à la section émetteur pour la transmission du signal. Par conséquent, le radar ne peut pas recevoir le signal pendant le temps de transmission.
De même, il relie l'antenne à la section récepteur pour la réception du signal. Le radar ne peut pas transmettre le signal pendant l'heure de réception. De cette manière, Duplexer isole à la fois les sections émetteur et récepteur.
Types de duplexeurs
Dans cette section, nous découvrirons les différents types de duplexeurs. Nous pouvons classer les duplexeurs dans ce qui suitthree types.
- Duplexeur de type branche
- Duplexeur équilibré
- Circulateur comme duplexeur
Dans nos sections suivantes, nous discuterons en détail des types de duplexeurs.
Duplexeur de type branche
Le duplexeur de type dérivation se compose de deux commutateurs: le commutateur de transmission-réception (TR) et le commutateur anti-transmission-réception (ATR). La figure suivante montre leblock diagram du duplexeur de type branche -

Comme le montre la figure, les deux interrupteurs, TR et ATR sont placés à une distance de $\lambda/4$ de la ligne de transmission et les deux commutateurs sont séparés par une distance de $\lambda/4$. leworking du duplexeur de type branche est mentionné ci-dessous.
Pendant transmission, TR et ATR ressembleront à un circuit ouvert de la ligne de transmission. Par conséquent, l'antenne sera connectée à l'émetteur via la ligne de transmission.
Pendant reception, ATR ressemblera à un court-circuit sur la ligne de transmission. Par conséquent, l'antenne sera connectée au récepteur via la ligne de transmission.
Le duplexeur de type branche ne convient que pour les radars à faible coût, car il a moins de capacité de gestion de puissance.
Duplexeur équilibré
Nous savons qu'un two-hole Directional Couplerest une jonction de guide d'ondes à 4 ports composée d'un guide d'ondes primaire et d'un guide d'ondes secondaire. Il y a deux petits trous, qui seront communs à ces deux guides d'ondes.
Le duplexeur équilibré se compose de deux tubes TR. La configuration du duplexeur équilibré pourtransmission l'objectif est illustré dans la figure suivante.

Le signal produit par l'émetteur doit atteindre l'antenne pour que l'antenne transmette ce signal pendant le temps de transmission. lesolid lines with arrow marks illustré dans la figure ci-dessus représente la façon dont le signal atteint l'antenne de l'émetteur.
Les lignes pointillées avec des flèches montrées dans la figure ci-dessus représentent le signal qui s'échappe des tubes Dual TR; cela n'atteindra que la charge correspondante. Ainsi, aucun signal n'a été atteint vers le récepteur.
La configuration du duplexeur équilibré pour reception l'objectif est illustré dans la figure ci-dessous.

Nous savons que Antenna reçoit le signal pendant le temps de réception. Le signal reçu par l'antenne doit atteindre le récepteur. lesolid lines with arrow marksmontré dans la figure ci-dessus représente la façon dont le signal atteint le récepteur de l'antenne. Dans ce cas, les tubes Dual TR transmettent le signal de la première section du guide d'ondes à la section suivante du guide d'ondes.
Le duplexeur équilibré a une capacité de gestion de puissance élevée et une bande passante élevée par rapport au duplexeur de type branche.
Circulateur comme duplexeur
Nous savons que le functionality du circulateur est que si nous appliquons une entrée à un port, alors elle sera produite au port, qui lui est adjacent dans le sens des aiguilles d'une montre. Il n'y a pas de sortie aux ports restants du circulateur.
Alors, envisagez un circulateur à 4 ports et connectez l'émetteur, l'antenne, le récepteur et la charge correspondante aux ports 1, 2, 3 et 4 respectivement. Maintenant, comprenons comment le4-port circulator fonctionne comme duplexeur.
Le signal, qui est produit par l'émetteur doit atteindre l'antenne pour que l'antenne transmette ce signal pendant transmissiontemps. Cet objectif sera atteint lorsque l'émetteur génère un signal au port1.
Le signal reçu par l'antenne doit atteindre le récepteur pendant receptiontemps. Cet objectif sera atteint lorsque l'antenne présente au port2 recevra un signal externe.
La figure suivante montre le block diagram du circulateur comme duplexeur -

La figure ci-dessus se compose d'un circulateur à 4 ports - l'émetteur, l'antenne et la charge adaptée sont connectés respectivement aux ports 1, 2 et 4 du circulateur, comme indiqué au début de la section.
Le récepteur n'est pas directement connecté au port3. Au lieu de cela, les blocs correspondant au limiteur TR passif sont placés entre le port 3 du circulateur et du récepteur. Les blocs, le tube TR et le limiteur de diode sont les blocs correspondant au limiteur TR passif.
En fait, le circulateur lui-même fait office de duplexeur. Il ne nécessite aucun bloc supplémentaire. Cependant, il ne donnera aucune protection au récepteur. Ainsi, les blocs correspondant au limiteur TR passif sont utilisés afin de fournir leprotection to the receiver.
Systèmes radar - Antennes multiéléments
Une seule antenne peut émettre une certaine quantité de puissance dans une direction particulière. De toute évidence, la quantité de puissance de rayonnement sera augmentée lorsque nous utilisons un groupe d'antennes ensemble. Le groupe d'antennes s'appelleAntenna array.
Un réseau d'antennes est un système rayonnant comprenant des radiateurs et des éléments. Chacun de ces radiateurs possède son propre champ d'induction. Les éléments sont placés si près que chacun se trouve dans le champ d'induction du voisin. Par conséquent, le diagramme de rayonnement produit par eux, serait levector sum des individuels.
Les antennes rayonnent individuellement et lorsqu'elles sont dans un réseau, le rayonnement de tous les éléments se résume, pour former le faisceau de rayonnement, qui a un gain élevé, une directivité élevée et de meilleures performances, avec des pertes minimales.
On dit qu'un réseau d'antennes est Phased Antenna array si la forme et la direction du diagramme de rayonnement dépendent des phases et amplitudes relatives des courants présents à chaque antenne de ce réseau.
Motif de radiation
Considérons `` n '' éléments de rayonnement isotropes, qui, lorsqu'ils sont combinés, forment un array. La figure ci-dessous vous aidera à comprendre la même chose. Laissez l'espacement entre les éléments successifs être des unités «d».

Comme le montre la figure, tous les éléments de rayonnement reçoivent le même signal entrant. Ainsi, chaque élément produit une tension de sortie égale de$sin \left ( \omega t \right)$. Cependant, il y aura un égalphase difference $\Psi$entre les éléments successifs. Mathématiquement, il peut s'écrire -
$$\Psi=\frac{2\pi d\sin\theta }{\lambda }\:\:\:\:\:Equation\:1$$
Où,
$\theta$ est l'angle auquel le signal entrant est incident sur chaque élément de rayonnement.
Mathématiquement, nous pouvons écrire les expressions pour output voltages de 'n' éléments de rayonnement individuellement comme
$$E_1=\sin\left [ \omega t \right]$$
$$E_2=\sin\left [\omega t+\Psi\right]$$
$$E_3=\sin\left [\omega t+2\Psi\right]$$
$$.$$
$$.$$
$$.$$
$$E_n=\sin\left [\omega t+\left (N-1\right )\Psi\right]$$
Où,
$E_1, E_2, E_3, …, E_n$sont les tensions de sortie des premier, deuxième, troisième,…, nième éléments de rayonnement respectivement.
$\omega$ est la fréquence angulaire du signal.
Nous obtiendrons le overall output voltage $E_a$du réseau en ajoutant les tensions de sortie de chaque élément présent dans ce réseau, puisque tous ces éléments de rayonnement sont connectés en réseau linéaire. Mathématiquement, il peut être représenté par -
$$E_a=E_1+E_2+E_3+ …+E_n \:\:\:Equation\:2$$
Substitute, les valeurs de $E_1, E_2, E_3, …, E_n$ dans l'équation 2.
$$E_a=\sin\left [ \omega t \right]+\sin\left [\omega t+\Psi\right ]+\sin\left [\omega t+2\Psi\right ]+\sin\left [\omega t+\left (n-1\right )\Psi\right]$$
$$\Rightarrow E_a=\sin\left [\omega t+\frac{(n-1)\Psi)}{2}\right ]\frac{\sin\left [\frac{n\Psi}{2}\right]}{\sin\left [\frac{\Psi}{2}\right ]}\:\:\:\:\:Equation\:3$$
Dans l'équation 3, il y a deux termes. Dès le premier terme, on peut observer que la tension de sortie globale$E_a$ est une onde sinusoïdale ayant une fréquence angulaire $\omega$. Mais, il a un déphasage de$\left (n−1\right )\Psi/2$. Le deuxième terme de l'équation 3 est unamplitude factor.
La magnitude de l'équation 3 sera
$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\Psi}{2}\right ]}{\sin\left [\frac{\Psi}{2}\right]} \right |\:\:\:\:\:Equation\:4$$
Nous obtiendrons l'équation suivante en remplaçant l'équation 1 dans l'équation 4.
$$\left | E_a \right|=\left | \frac{\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right]}{\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]} \right |\:\:\:\:\:Equation\:5$$
L'équation 5 est appelée field intensity pattern. Le modèle d'intensité de champ aura les valeurs de zéros lorsque le numérateur de l'équation 5 est zéro
$$\sin\left [\frac{n\pi d\sin\theta}{\lambda}\right ]=0$$
$$\Rightarrow \frac{n\pi d\sin\theta}{\lambda}=\pm m\pi$$
$$\Rightarrow nd\sin\theta=\pm m\lambda$$
$$\Rightarrow \sin\theta=\pm \frac{m\lambda}{nd}$$
Où,
$m$ est un entier et il est égal à 1, 2, 3 et ainsi de suite.
Nous pouvons trouver le maximum valuesdu modèle d'intensité de champ en utilisant la règle L-Hospital lorsque le numérateur et le dénominateur de l'équation 5 sont égaux à zéro. Nous pouvons observer que si le dénominateur de l'équation 5 devient zéro, alors le numérateur de l'équation 5 devient également zéro.
Maintenant, obtenons la condition pour laquelle le dénominateur de l'équation 5 devient zéro.
$$\sin\left [\frac{\pi d\sin\theta}{\lambda}\right ]=0$$
$$\Rightarrow \frac{\pi d\sin\theta}{\lambda}=\pm p\pi$$
$$\Rightarrow d\sin\theta=\pm p\lambda$$
$$\Rightarrow \sin\theta=\pm \frac{p\lambda}{d}$$
Où,
$p$ est un entier égal à 0, 1, 2, 3 et ainsi de suite.
Si nous considérons $p$ comme zéro, alors nous obtiendrons la valeur de $\sin\theta$comme zéro. Dans ce cas, nous obtiendrons la valeur maximale du motif d'intensité de champ correspondant aumain lobe. Nous obtiendrons les valeurs maximales du modèle d'intensité de champ correspondant àside lobes, quand on considère d'autres valeurs de $p$.
La direction du diagramme de rayonnement du réseau phasé peut être orientée en faisant varier les phases relatives du courant présent à chaque antenne. C'est leadvantage de réseau phasé à balayage électronique.