एअर इंडिया - लोकप्रिय खोज एल्गोरिदम
खोज एआई में समस्या समाधान की सार्वभौमिक तकनीक है। टाइल गेम, सुडोकू, क्रॉसवर्ड आदि जैसे कुछ एकल-खिलाड़ी गेम हैं। खोज एल्गोरिदम आपको ऐसे खेलों में किसी विशेष स्थिति की खोज करने में मदद करते हैं।
सिंगल एजेंट पाथफाइंडिंग समस्याएं
3X3 आठ-टाइल, 4X4 पंद्रह-टाइल, और 5X5 चौबीस टाइल पहेली जैसे खेल एकल-एजेंट-पथ-खोज चुनौतियां हैं। वे एक खाली टाइल के साथ टाइलों के एक मैट्रिक्स से मिलकर होते हैं। खिलाड़ी को किसी उद्देश्य को पूरा करने के उद्देश्य से एक खपरैल में क्षैतिज या क्षैतिज रूप से एक टाइल फिसलने से व्यवस्थित करने की आवश्यकता होती है।
सिंगल एजेंट पाथफाइंडिंग समस्याओं के अन्य उदाहरण हैं ट्रैवलिंग सेल्समैन प्रॉब्लम, रूबिक क्यूब और थ्योरम प्रोविंग।
शब्दावली खोजें
Problem Space- यह वह वातावरण है जिसमें खोज होती है। (राज्यों का एक सेट और उन राज्यों को बदलने के लिए ऑपरेटरों का सेट)
Problem Instance - यह इनिशियल स्टेट + गोल स्टेट है।
Problem Space Graph- यह समस्या की स्थिति का प्रतिनिधित्व करता है। राज्यों को नोड्स द्वारा दिखाया जाता है और ऑपरेटरों को किनारों द्वारा दिखाया जाता है।
Depth of a problem - प्रारंभिक राज्य से लक्ष्य राज्य के लिए एक छोटी पथ की लंबाई या ऑपरेटरों का सबसे छोटा अनुक्रम।
Space Complexity - मेमोरी में संग्रहीत नोड्स की अधिकतम संख्या।
Time Complexity - अधिकतम संख्या में नोड बनाए जाते हैं।
Admissibility - एक एल्गोरिथ्म की एक संपत्ति हमेशा एक इष्टतम समाधान खोजने के लिए।
Branching Factor - समस्या अंतरिक्ष ग्राफ में बच्चे की औसत संख्या।
Depth - प्रारंभिक अवस्था से लक्ष्य अवस्था तक के सबसे छोटे मार्ग की लंबाई।
जानवर-बल खोज रणनीतियाँ
वे सबसे सरल हैं, क्योंकि उन्हें किसी भी डोमेन-विशिष्ट ज्ञान की आवश्यकता नहीं है। वे कम संख्या में संभव राज्यों के साथ ठीक काम करते हैं।
आवश्यकताएँ -
- राज्य का विवरण
- वैध ऑपरेटरों का एक सेट
- प्रारम्भिक अवस्था
- लक्ष्य की स्थिति का वर्णन
पहले चौड़ाई खोजो
यह रूट नोड से शुरू होता है, पहले पड़ोसी नोड्स की खोज करता है और अगले स्तर के पड़ोसियों की ओर बढ़ता है। यह एक समय में एक पेड़ उत्पन्न करता है जब तक कि समाधान नहीं मिलता है। इसे FIFO कतार डेटा संरचना का उपयोग करके लागू किया जा सकता है। यह विधि समाधान के लिए सबसे छोटा रास्ता प्रदान करती है।
अगर branching factor(किसी दिए गए नोड के लिए बच्चे की औसत संख्या) = बी और गहराई = डी, फिर स्तर डी = बी डी पर नोड्स की संख्या ।
सबसे खराब स्थिति में बनाए गए नोड्स की कुल संख्या b + b 2 + b 3 +… + b d है ।
Disadvantage- चूंकि प्रत्येक स्तर के नोड्स को अगले एक को बनाने के लिए सहेजा जाता है, इसलिए यह बहुत अधिक मेमोरी स्पेस का उपभोग करता है। नोड्स को स्टोर करने के लिए अंतरिक्ष की आवश्यकता घातीय है।
इसकी जटिलता नोड्स की संख्या पर निर्भर करती है। यह डुप्लिकेट नोड्स की जांच कर सकता है।

गहराई-पहली खोज
इसे LIFO स्टैक डेटा संरचना के साथ पुनरावृत्ति में कार्यान्वित किया जाता है। यह चौड़ाई के रूप में नोड्स का एक ही सेट बनाता है, केवल अलग क्रम में।
चूंकि रूट से लीफ नोड तक प्रत्येक मार्ग में एकल पथ पर नोड्स संग्रहीत होते हैं, नोड्स को संग्रहीत करने के लिए स्थान की आवश्यकता रैखिक होती है। ब्रांचिंग फैक्टर b और m के रूप में गहराई के साथ , स्टोरेज स्पेस bm है।
Disadvantage- यह एल्गोरिथ्म समाप्त नहीं हो सकता है और एक मार्ग पर असीम रूप से जा सकता है। इस मुद्दे का समाधान कट-ऑफ गहराई चुनना है। यदि आदर्श कट-ऑफ d है , और यदि चुना हुआ कट-ऑफ d से कम है , तो यह एल्गोरिथम विफल हो सकता है। यदि चुना हुआ कट-ऑफ d से अधिक है , तो निष्पादन समय बढ़ जाता है।
इसकी जटिलता पथों की संख्या पर निर्भर करती है। यह डुप्लिकेट नोड्स की जाँच नहीं कर सकता है।

अप्रत्यक्ष खोज
यह प्रारंभिक अवस्था से और लक्ष्य राज्य से पिछड़े दोनों को एक सामान्य अवस्था की पहचान करने के लिए मिलते हैं।
प्रारंभिक अवस्था से पथ को लक्ष्य अवस्था से व्युत्क्रम पथ के साथ मिलाया जाता है। प्रत्येक खोज कुल पथ के आधे हिस्से तक ही की जाती है।
यूनिफ़ॉर्म कॉस्ट सर्च
एक नोड के लिए मार्ग की बढ़ती लागत में छंटाई की जाती है। यह हमेशा कम से कम लागत नोड का विस्तार करता है। यदि यह प्रत्येक संक्रमण की समान लागत है, तो यह चौड़ाई प्रथम खोज के समान है।
यह लागत के बढ़ते क्रम में रास्तों की पड़ताल करता है।
Disadvantage- लागत। C * के साथ कई लंबे रास्ते हो सकते हैं। यूनिफ़ॉर्म कॉस्ट सर्च को उन सभी का पता लगाना चाहिए।
Iterative गहरीकरण गहराई-पहली खोज
यह गहराई-पहली खोज को स्तर 1 पर करता है, शुरू होता है, पूर्ण गहराई-प्रथम खोज को स्तर 2 तक ले जाता है, और इस तरह से समाधान मिलने तक जारी रहता है।
यह कभी भी एक नोड नहीं बनाता है जब तक कि सभी निचले नोड उत्पन्न नहीं होते हैं। यह केवल नोड्स के ढेर को बचाता है। एल्गोरिथ्म तब समाप्त होता है जब वह गहराई पर घ का समाधान पाता है । गहराई d पर निर्मित नोड्स की संख्या b d है और गहराई d-1 पर b d-1 है।
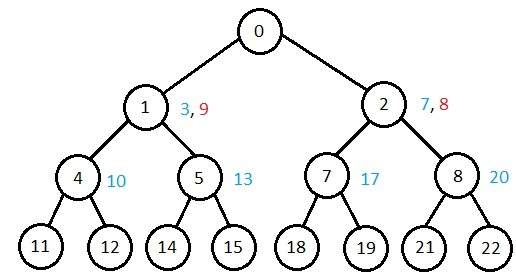
विभिन्न एल्गोरिदम जटिलताओं की तुलना
आइए हम विभिन्न मानदंडों के आधार पर एल्गोरिदम के प्रदर्शन को देखते हैं -
| मापदंड | चौड़ाई प्रथम | गहराई पहले | द्विदिश | यूनिफ़ॉर्म कॉस्ट | इंटरएक्टिव गहरीकरण |
|---|---|---|---|---|---|
| समय | b d | बी एम | b d / 2 | b d | b d |
| अंतरिक्ष | b d | बी एम | b d / 2 | b d | b d |
| optimality | हाँ | नहीं | हाँ | हाँ | हाँ |
| संपूर्णता | हाँ | नहीं | हाँ | हाँ | हाँ |
सूचित (हेयुरिस्टिक) खोज रणनीतियाँ
बड़ी संख्या में संभावित राज्यों के साथ बड़ी समस्याओं को हल करने के लिए, खोज एल्गोरिदम की दक्षता बढ़ाने के लिए समस्या-विशिष्ट ज्ञान को जोड़ा जाना चाहिए।
अनुमानी मूल्यांकन कार्य
वे दो राज्यों के बीच इष्टतम पथ की लागत की गणना करते हैं। स्लाइडिंग-टाइल गेम के लिए एक हेयुरिस्टिक फ़ंक्शन की गणना गणना की गई चालों की संख्या द्वारा की जाती है, जो प्रत्येक टाइल अपने लक्ष्य राज्य से बनाती है और सभी टाइलों के लिए इन संख्याओं को जोड़ती है।
शुद्ध अनुमानी खोज
यह उनके विधर्मी मूल्यों के क्रम में नोड्स का विस्तार करता है। यह दो सूची बनाता है, पहले से विस्तारित नोड्स के लिए एक बंद सूची और निर्मित लेकिन अनएक्सपैंडेड नोड्स के लिए एक खुली सूची।
प्रत्येक पुनरावृत्ति में, एक न्यूनतम हेयुरिस्टिक मूल्य के साथ एक नोड का विस्तार किया जाता है, उसके सभी बच्चे नोड्स को बंद सूची में बनाया और रखा जाता है। फिर, हेयुरिस्टिक फ़ंक्शन को चाइल्ड नोड्स पर लागू किया जाता है और उन्हें उनके हेयुरिस्टिक मूल्य के अनुसार खुली सूची में रखा जाता है। छोटे रास्तों को बचाया जाता है और लंबे समय तक निपटाया जाता है।
एक खोज
यह बेस्ट फर्स्ट सर्च का सबसे प्रसिद्ध रूप है। यह उन रास्तों का विस्तार करने से बचता है जो पहले से ही महंगे हैं, लेकिन सबसे अधिक आशाजनक रास्तों का विस्तार करता है।
f (n) = g (n) + h (n), जहां
- जी (एन) नोड तक पहुंचने के लिए लागत (अब तक)
- h (n) नोड से लक्ष्य तक पहुंचने के लिए अनुमानित लागत
- f (n) लक्ष्य के लिए n के माध्यम से पथ की कुल लागत का अनुमान है। इसे f (n) बढ़ाकर प्राथमिकता कतार का उपयोग करके लागू किया गया है।
लालची बेस्ट फर्स्ट सर्च
यह उस नोड का विस्तार करता है जिसका अनुमान लक्ष्य के सबसे करीब है। यह f (n) = h (n) पर आधारित नोड्स का विस्तार करता है। इसे प्राथमिकता कतार का उपयोग करके लागू किया गया है।
Disadvantage- यह छोरों में फंस सकता है। यह इष्टतम नहीं है।
स्थानीय खोज एल्गोरिदम
वे एक संभावित समाधान से शुरू करते हैं और फिर पड़ोसी समाधान में चले जाते हैं। वे समाप्त होने से पहले किसी भी समय बाधित होने पर भी एक वैध समाधान लौटा सकते हैं।
पहाड़ी पर चढ़ने की खोज
यह एक पुनरावृत्त एल्गोरिथ्म है जो किसी समस्या के मनमाने समाधान के साथ शुरू होता है और समाधान के एक तत्व को वृद्धिशील रूप से बदलकर एक बेहतर समाधान खोजने का प्रयास करता है। यदि परिवर्तन बेहतर समाधान उत्पन्न करता है, तो एक वृद्धिशील परिवर्तन को नए समाधान के रूप में लिया जाता है। इस प्रक्रिया को तब तक दोहराया जाता है जब तक कि आगे कोई सुधार न हो।
फ़ंक्शन हिल-क्लाइम्बिंग (समस्या), एक स्थानीय अधिकतम राज्य देता है।
inputs: problem, a problem
local variables: current, a node
neighbor, a node
current <-Make_Node(Initial-State[problem])
loop
do neighbor <- a highest_valued successor of current
if Value[neighbor] ≤ Value[current] then
return State[current]
current <- neighbor
endDisadvantage - यह एल्गोरिथ्म न तो पूर्ण है, न ही इष्टतम।
स्थानीय बीम खोज
इस एल्गोरिथ्म में, यह किसी भी समय राज्यों की संख्या रखता है। शुरुआत में, ये राज्य अनियमित रूप से उत्पन्न होते हैं। इन k राज्यों के उत्तराधिकारियों की गणना उद्देश्य फ़ंक्शन की सहायता से की जाती है। यदि इन उत्तराधिकारियों में से कोई भी उद्देश्य फ़ंक्शन का अधिकतम मूल्य है, तो एल्गोरिथ्म बंद हो जाता है।
अन्यथा (प्रारंभिक k राज्यों और राज्यों के उत्तराधिकारियों की संख्या = 2k) राज्यों को एक पूल में रखा गया है। पूल को तब संख्यात्मक रूप से क्रमबद्ध किया जाता है। उच्चतम k राज्यों को नए प्रारंभिक राज्यों के रूप में चुना जाता है। यह प्रक्रिया तब तक जारी रहती है जब तक कि अधिकतम मूल्य नहीं मिल जाता।
फ़ंक्शन BeamSearch ( समस्या, k ), एक समाधान स्थिति देता है।
start with k randomly generated states
loop
generate all successors of all k states
if any of the states = solution, then return the state
else select the k best successors
endतैयार किए हुयी धातु पे पानी चढाने की कला
एनीलिंग एक धातु को गर्म करने और ठंडा करने की प्रक्रिया है जो इसके भौतिक गुणों को संशोधित करने के लिए इसकी आंतरिक संरचना को बदलने के लिए है। जब धातु ठंडा हो जाती है, तो इसकी नई संरचना को जब्त कर लिया जाता है, और धातु अपने नए प्राप्त गुणों को बरकरार रखता है। नकली एनालिंग प्रक्रिया में, तापमान को परिवर्तनशील रखा जाता है।
हम शुरू में तापमान को ऊंचा करते हैं और फिर एल्गोरिथ्म आगे बढ़ते हुए इसे धीरे-धीरे 'शांत' करने की अनुमति देते हैं। जब तापमान अधिक होता है, तो एल्गोरिथ्म को उच्च आवृत्ति के साथ खराब समाधान स्वीकार करने की अनुमति दी जाती है।
शुरू
- प्रारंभिक k = 0; एल = चर की पूर्णांक संख्या;
- I → j से, प्रदर्शन अंतर search खोजें।
- यदि Δ <= 0 तो अन्य को स्वीकार करें यदि ऍक्स्प (-T / टी (के))> यादृच्छिक (0,1) तो स्वीकार करें;
- एल (के) चरणों के लिए चरण 1 और 2 दोहराएं।
- k = k + 1;
मापदंड पूरा होने तक चरण 1 को 4 से दोहराएं।
समाप्त
ट्रैवलिंग सेल्समैन की समस्या
इस एल्गोरिथ्म में, उद्देश्य एक कम लागत वाले दौरे को खोजना है जो एक शहर से शुरू होता है, सभी शहरों में एक बार एन-रूट पर जाता है और एक ही शुरुआती शहर में समाप्त होता है।
Start
Find out all (n -1)! Possible solutions, where n is the total number of cities.
Determine the minimum cost by finding out the cost of each of these (n -1)! solutions.
Finally, keep the one with the minimum cost.
end