बिग डेटा एनालिटिक्स - सांख्यिकीय तरीके
डेटा का विश्लेषण करते समय, सांख्यिकीय दृष्टिकोण होना संभव है। बुनियादी विश्लेषण करने के लिए आवश्यक बुनियादी उपकरण हैं -
- सहसंबंध विश्लेषण
- भिन्नता का विश्लेषण
- परिकल्पना परीक्षण
बड़े डेटासेट के साथ काम करते समय, इसमें कोई समस्या शामिल नहीं होती है क्योंकि ये तरीके कॉरेलेशन एनालिसिस के अपवाद के साथ कम्प्यूटेशनल रूप से गहन नहीं होते हैं। इस मामले में, नमूना लेना हमेशा संभव होता है और परिणाम मजबूत होना चाहिए।
सहसंबंध विश्लेषण
सहसंबंध विश्लेषण संख्यात्मक चर के बीच रैखिक संबंधों को खोजने का प्रयास करता है। यह विभिन्न परिस्थितियों में उपयोग किया जा सकता है। एक सामान्य उपयोग खोजपूर्ण डेटा विश्लेषण है, पुस्तक के खंड 16.0.2 में इस दृष्टिकोण का एक मूल उदाहरण है। सबसे पहले, उल्लेखित उदाहरण में प्रयुक्त सहसंबंध मीट्रिक पर आधारित हैPearson coefficient। हालाँकि, सहसंबंध का एक और दिलचस्प मीट्रिक है जो आउटलेर्स से प्रभावित नहीं है। इस मीट्रिक को स्पीयरमैन सहसंबंध कहा जाता है।
spearman correlation मीट्रिक पियरसन विधि की तुलना में आउटलेर्स की उपस्थिति के लिए अधिक मजबूत है और डेटा के सामान्य रूप से वितरित नहीं होने पर संख्यात्मक चर के बीच रैखिक संबंधों का बेहतर अनुमान देता है।
library(ggplot2)
# Select variables that are interesting to compare pearson and spearman
correlation methods.
x = diamonds[, c('x', 'y', 'z', 'price')]
# From the histograms we can expect differences in the correlations of both
metrics.
# In this case as the variables are clearly not normally distributed, the
spearman correlation
# is a better estimate of the linear relation among numeric variables.
par(mfrow = c(2,2))
colnm = names(x)
for(i in 1:4) {
hist(x[[i]], col = 'deepskyblue3', main = sprintf('Histogram of %s', colnm[i]))
}
par(mfrow = c(1,1))निम्नलिखित आकृति में हिस्टोग्राम से हम दोनों मैट्रिक्स के सहसंबंधों में अंतर की उम्मीद कर सकते हैं। इस मामले में, चूँकि चर स्पष्ट रूप से वितरित नहीं होते हैं, इसलिए स्पीयरमैन सहसंबंध एक दूसरे के बीच के संबंध का एक बेहतर अनुमान है।
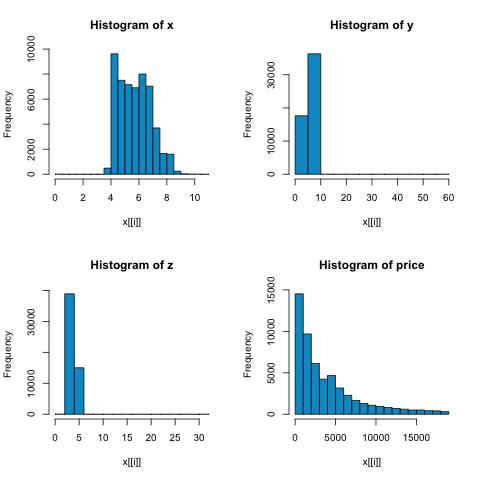
आर में सहसंबंध की गणना करने के लिए, फ़ाइल खोलें bda/part2/statistical_methods/correlation/correlation.R यह कोड अनुभाग है।
## Correlation Matrix - Pearson and spearman
cor_pearson <- cor(x, method = 'pearson')
cor_spearman <- cor(x, method = 'spearman')
### Pearson Correlation
print(cor_pearson)
# x y z price
# x 1.0000000 0.9747015 0.9707718 0.8844352
# y 0.9747015 1.0000000 0.9520057 0.8654209
# z 0.9707718 0.9520057 1.0000000 0.8612494
# price 0.8844352 0.8654209 0.8612494 1.0000000
### Spearman Correlation
print(cor_spearman)
# x y z price
# x 1.0000000 0.9978949 0.9873553 0.9631961
# y 0.9978949 1.0000000 0.9870675 0.9627188
# z 0.9873553 0.9870675 1.0000000 0.9572323
# price 0.9631961 0.9627188 0.9572323 1.0000000ची-स्क्वाड टेस्ट
ची-स्क्वैयर परीक्षण हमें यह जांचने की अनुमति देता है कि क्या दो यादृच्छिक चर स्वतंत्र हैं। इसका अर्थ है कि प्रत्येक चर का प्रायिकता वितरण दूसरे को प्रभावित नहीं करता है। आर में परीक्षण का मूल्यांकन करने के लिए हमें एक आकस्मिक तालिका बनाने की आवश्यकता है, और फिर तालिका को पास करेंchisq.test R समारोह।
उदाहरण के लिए, आइए देखें कि क्या चर के बीच एक संबंध है: हीरे के डाटासेट से कट और रंग। परीक्षण को औपचारिक रूप से परिभाषित किया गया है -
- H0: वेरिएबल कट और डायमंड स्वतंत्र हैं
- H1: वेरिएबल कट और डायमंड स्वतंत्र नहीं हैं
हम मान लेंगे कि उनके नाम से इन दो चर के बीच एक संबंध है, लेकिन परीक्षण एक उद्देश्य "नियम" कह सकता है कि यह परिणाम कितना महत्वपूर्ण है या नहीं।
निम्नलिखित कोड स्निपेट में, हमने पाया कि परीक्षण का पी-मूल्य 2.2e-16 है, यह व्यावहारिक रूप से लगभग शून्य है। फिर टेस्ट करने के बाद एMonte Carlo simulation, हमने पाया कि पी-वैल्यू 0.0004998 है जो अभी भी थ्रेशोल्ड 0.05 से काफी कम है। इस परिणाम का अर्थ है कि हम अशक्त परिकल्पना (H0) को अस्वीकार करते हैं, इसलिए हम चर मानते हैंcut तथा color स्वतंत्र नहीं हैं।
library(ggplot2)
# Use the table function to compute the contingency table
tbl = table(diamonds$cut, diamonds$color)
tbl
# D E F G H I J
# Fair 163 224 312 314 303 175 119
# Good 662 933 909 871 702 522 307
# Very Good 1513 2400 2164 2299 1824 1204 678
# Premium 1603 2337 2331 2924 2360 1428 808
# Ideal 2834 3903 3826 4884 3115 2093 896
# In order to run the test we just use the chisq.test function.
chisq.test(tbl)
# Pearson’s Chi-squared test
# data: tbl
# X-squared = 310.32, df = 24, p-value < 2.2e-16
# It is also possible to compute the p-values using a monte-carlo simulation
# It's needed to add the simulate.p.value = TRUE flag and the amount of
simulations
chisq.test(tbl, simulate.p.value = TRUE, B = 2000)
# Pearson’s Chi-squared test with simulated p-value (based on 2000 replicates)
# data: tbl
# X-squared = 310.32, df = NA, p-value = 0.0004998टी परीक्षण
के विचार t-testमूल्यांकन करना है कि क्या नाममात्र चर के विभिन्न समूहों के बीच एक संख्यात्मक चर # वितरण में अंतर हैं। इसे प्रदर्शित करने के लिए, मैं फैक्टर वेरिएबल कट के फेयर और आइडियल लेवल का चयन करूंगा, फिर हम उन दो समूहों के बीच एक न्यूमेरिकल वैरिएबल के मानों की तुलना करेंगे।
data = diamonds[diamonds$cut %in% c('Fair', 'Ideal'), ]
data$cut = droplevels.factor(data$cut) # Drop levels that aren’t used from the
cut variable
df1 = data[, c('cut', 'price')]
# We can see the price means are different for each group
tapply(df1$price, df1$cut, mean)
# Fair Ideal
# 4358.758 3457.542टी-परीक्षणों को आर के साथ लागू किया जाता है t.testसमारोह। T.test का सूत्र इंटरफ़ेस इसका उपयोग करने का सबसे सरल तरीका है, विचार यह है कि एक संख्यात्मक चर को समूह चर द्वारा समझाया गया है।
उदाहरण के लिए: t.test(numeric_variable ~ group_variable, data = data)। पिछले उदाहरण में, एnumeric_variable है price और यह group_variable है cut।
सांख्यिकीय परिप्रेक्ष्य से, हम परीक्षण कर रहे हैं कि दो समूहों के बीच संख्यात्मक चर के वितरण में अंतर है या नहीं। औपचारिक रूप से परिकल्पना परीक्षण एक अशक्त (H0) परिकल्पना और एक वैकल्पिक परिकल्पना (H1) के साथ वर्णित है।
H0: फेयर और आइडियल ग्रुप के बीच प्राइस वैरिएबल के डिस्ट्रीब्यूशन में कोई अंतर नहीं हैं
H1 फेयर और आइडियल ग्रुप के बीच प्राइस वैरिएबल के डिस्ट्रीब्यूशन में अंतर हैं
निम्नलिखित कोड के साथ आर में निम्नलिखित लागू किया जा सकता है -
t.test(price ~ cut, data = data)
# Welch Two Sample t-test
#
# data: price by cut
# t = 9.7484, df = 1894.8, p-value < 2.2e-16
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# 719.9065 1082.5251
# sample estimates:
# mean in group Fair mean in group Ideal
# 4358.758 3457.542
# Another way to validate the previous results is to just plot the
distributions using a box-plot
plot(price ~ cut, data = data, ylim = c(0,12000),
col = 'deepskyblue3')हम जाँच कर सकते हैं कि पी-मान 0.05 से कम है या नहीं। यदि यह मामला है, तो हम वैकल्पिक परिकल्पना रखते हैं। इसका मतलब है कि हमने कटौती कारक के दो स्तरों के बीच कीमत के अंतर को पाया है। स्तरों के नाम से हम इस परिणाम की उम्मीद करेंगे, लेकिन हमें उम्मीद नहीं थी कि विफल समूह में औसत मूल्य आदर्श समूह की तुलना में अधिक होगा। हम इसे प्रत्येक कारक के साधनों की तुलना करके देख सकते हैं।
plotकमांड एक ग्राफ का उत्पादन करता है जो मूल्य और कटौती चर के बीच संबंध दिखाता है। यह एक बॉक्स-प्लॉट है; हमने इस प्लॉट को खंड 16.0.1 में शामिल किया है, लेकिन यह मूल रूप से कट विश्लेषण के दो स्तरों के लिए मूल्य चर का वितरण दिखाता है।
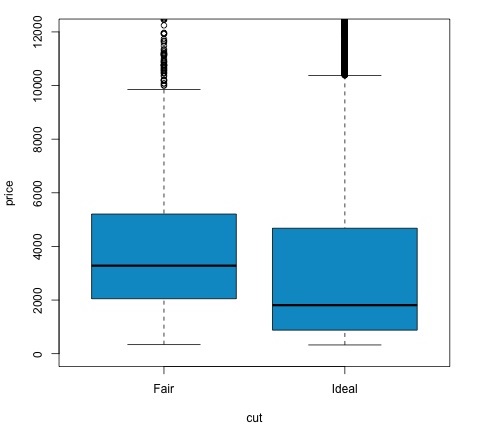
भिन्नता का विश्लेषण
Variance (ANOVA) का विश्लेषण एक सांख्यिकीय मॉडल है जिसका उपयोग समूह वितरण के बीच अंतर का विश्लेषण करने के लिए किया जाता है, प्रत्येक समूह के माध्य और विचरण की तुलना करके, मॉडल का विकास रोनाल्ड फिशर द्वारा किया गया था। एनोवा कई समूहों के साधन बराबर हैं या नहीं, का एक सांख्यिकीय परीक्षण प्रदान करता है, और इसलिए दो से अधिक समूहों के लिए टी-परीक्षण को सामान्य करता है।
ANOVAs सांख्यिकीय महत्व के लिए तीन या अधिक समूहों की तुलना करने के लिए उपयोगी हैं क्योंकि कई दो-नमूना टी-परीक्षण करने से सांख्यिकीय प्रकार I त्रुटि होने की संभावना बढ़ जाएगी।
गणितीय स्पष्टीकरण प्रदान करने के संदर्भ में, परीक्षण को समझने के लिए निम्नलिखित की आवश्यकता है।
x ij = x + (x i - x) + (x ij - x)
यह निम्नलिखित मॉडल की ओर जाता है -
x ij = μ + α i + j ij
जहाँ μ भव्य माध्य है और α i ith समूह माध्य है। त्रुटि अवधि ∈ ij माना जाता है एक सामान्य वितरण से आईआईडी किया जाना है। परीक्षण की शून्य परिकल्पना यह है कि -
α 1 = α 2 = ... = α k
टेस्ट स्टेटिस्टिक कंप्यूटिंग के संदर्भ में, हमें दो मूल्यों की गणना करने की आवश्यकता है -
- समूह अंतर के बीच वर्गों के योग -
$$ SSD_B = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x _ {\ bar {i}}} - \ bar {x}) ^ 2 $ $
- समूहों के भीतर वर्गों की रकम
$$ SSD_W = \ sum_ {i} ^ {k} \ sum_ {j} ^ {n} (\ bar {x_ {बार {ij}}} - \ bar {x_ {बार {i}}}) ^ 2 $$
जहां SSD B के पास k SS 1 की स्वतंत्रता है और SSD W के पास N। k की स्वतंत्रता की डिग्री है। तब हम प्रत्येक मीट्रिक के लिए माध्य चुकता अंतर को परिभाषित कर सकते हैं।
एमएस बी = एसएसडी बी / (के - 1)
एमएस डब्ल्यू = एसएसडी डब्ल्यू / (एन - के)
अंत में, एनोवा में परीक्षण सांख्यिकीय को उपरोक्त दो मात्राओं के अनुपात के रूप में परिभाषित किया गया है
एफ = एमएस बी / एमएस डब्ल्यू
जो k and 1 और N of k स्वतंत्रता की डिग्री के साथ एक एफ-वितरण का अनुसरण करता है । यदि शून्य परिकल्पना सच है, तो F की संभावना लगभग 1 होगी। अन्यथा, समूह के बीच का मतलब वर्ग MSB बड़े होने की संभावना है, जिसके परिणामस्वरूप एक बड़ा F मान होता है।
मूलतः, ANOVA कुल विचरण के दो स्रोतों की जाँच करता है और देखता है कि कौन सा भाग अधिक योगदान देता है। यही कारण है कि इसे विचरण का विश्लेषण कहा जाता है, हालांकि इरादा समूह साधनों की तुलना करना है।
आंकड़े की गणना के संदर्भ में, यह वास्तव में आर में करने के लिए सरल है। निम्नलिखित उदाहरण प्रदर्शित करेगा कि यह कैसे किया जाता है और परिणामों की साजिश करता है।
library(ggplot2)
# We will be using the mtcars dataset
head(mtcars)
# mpg cyl disp hp drat wt qsec vs am gear carb
# Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
# Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
# Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
# Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
# Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
# Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
# Let's see if there are differences between the groups of cyl in the mpg variable.
data = mtcars[, c('mpg', 'cyl')]
fit = lm(mpg ~ cyl, data = mtcars)
anova(fit)
# Analysis of Variance Table
# Response: mpg
# Df Sum Sq Mean Sq F value Pr(>F)
# cyl 1 817.71 817.71 79.561 6.113e-10 ***
# Residuals 30 308.33 10.28
# Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 .
# Plot the distribution
plot(mpg ~ as.factor(cyl), data = mtcars, col = 'deepskyblue3')कोड निम्न आउटपुट का उत्पादन करेगा -

उदाहरण में हमें जो पी-वैल्यू मिलती है, वह 0.05 की तुलना में काफी छोटा है, इसलिए आर इसको दर्शाने के लिए '***' का प्रतीक देता है। इसका अर्थ है कि हम अशक्त परिकल्पना को अस्वीकार करते हैं और हम mpg के बीच के विभिन्न समूहों के बीच अंतर पाते हैंcyl चर।